線性插值在分配飛機整流罩氣動載荷中的應用

劉 偉

（中航西安飛機工業集團股份有限公司，陜西 西安 710089）

0 引言

飛機上的整流罩常由面板和骨架組成，主要是對內部的各個設備起包絡、氣動維形的作用，不參與全機受力，屬于次承力結構，在對結構強度進行設計時，主要考慮氣動載荷的分布，慣性載荷可以忽略不計[1-3]。現成的針對如何將理論計算或風洞測壓試驗的氣動載荷施加到有限元模型上的商業軟件較少且通用性不好，一般都是通過編程對氣動數據進行后置處理或對CAE軟件進行二次開發，目前常用的方法是選取與設計工與工況似的氣動載荷，將分布氣動載荷積分轉換為節點力，再遵循靜力等效原則，采用三點排或多點排方法轉換到有限元節點上[4-5]。

該文根據飛機的運動參數，篩選出整流罩的設計工況[6]，采用線性插值方法將各壓力點的氣動數據精確插值到設計工況，將每個氣動網格離散為多個網格，形成密網格；按照分布等效原則，將氣動載荷直接等效到有限元模型上，省略分布力轉換為節點力的中間過程，解決了通用性問題，提高了工作效率。

1 計算方法

為了獲取精確的整流罩氣動載荷，將整流罩視為外掛物，按照規范求解飛機在不同高度、速度以及受載情況下帶外掛物時全機的運動參數，并對其進行插值計算，得到整流罩的總氣動載荷，篩選出整流罩嚴重載荷情況作為設計工況，依據壓力分布數值計算數據或風洞測壓試驗數據，采用線性插值方法將各壓力數據插值到設計工況，形成密氣動網格，再轉換到有限元模型上。

1.1 計算假設

為了盡可能精確地得到有限元模型上的氣動分布載荷，計算需要基于以下3個假設：1）相鄰節點的壓力系數線性分布。2）氣動外形與有限元模型一致。3）氣動外形光滑、無突變。

壓力系數線性分布是插值計算的基礎，氣動外形光滑、無突變以及與有限元模型一致是保證精度的前提。

1.2 設計工況選取

選取整流罩的嚴重載荷情況時，一般會忽略慣性載荷，只考慮氣動載荷，應該考慮以下2個方面：1）3個方向合力及矩的極值。2）組合力及矩的極值。

以上2個方面共包括28個嚴重載荷情況，在實際工程中，考慮到整流罩的實際承載情況，大多數嚴重工況的載荷是可以忽略不計的。

1.3 設計工況插值

整流罩壓力分布數據一般是通過計算壓力分布數值或通過風洞測壓試驗獲得的，不同的計算軟件、風洞得到的數據格式不一致。常見的格式見表1和表2。

表1 壓力分布數值計算結果

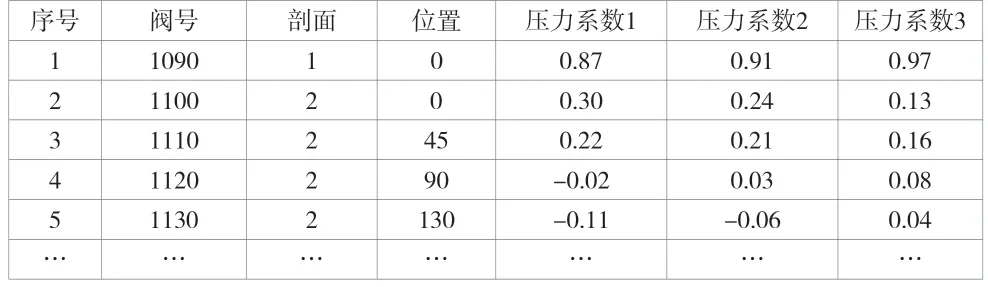
表2 風洞測壓試驗結果

表1和表2只是一些典型的數據格式，為了便于數據管理，對數據進行插值計算，統一氣動數據的格式，每個壓力點按照側滑角、攻角、馬赫數以及舵面偏角等組成數據矩陣并進行線性插值，得到整流罩在設計工況下的壓力分布，各壓力點的典型數據矩陣見表3。

表3 壓力點典型數據矩陣

表3中，“9類數據參數：2 3 2 1001”代表ID為1001的壓力點由2個側滑角、3個攻角以及2個馬赫數組成數據類型為9的數據矩陣；“6 9”為側滑角；“1 2 5”為攻角；“0.45 0.6”為馬赫數；其余數據為壓力系數。

1.4 離散氣動數據

壓力分布數值計算（CFD）得到的數據是以網格為基準而給出的，可以根據前期的劃分將CFD分為若干數據塊（包括I行×J列個數據點），代表不同的飛機部件或部件的一部分，每個數據塊可分為I個小塊，代表I行；每個小塊都包括J行數據，代表J列（如圖1所示），圖1呈現了上面描述的CFD數據的特點。每行數據包括網格坐標、網格面積以及網格3個方向的法向量和壓力系數。CFD數據自身的特點為該文的插值方法提供了數據基礎。氣動數據離散的基礎是每個數據塊可以嚴格的按I行J列進行數據排列，每行數據都包括滿足計算要求的數據。將每個氣動網格離散為多個網格，分為行的離散和列的離散，就是將每一行（列）相鄰的2個點看作一組數據的起點和終點，按照空間距離進行線性插值，得到一組全新的數據，如圖1所示。

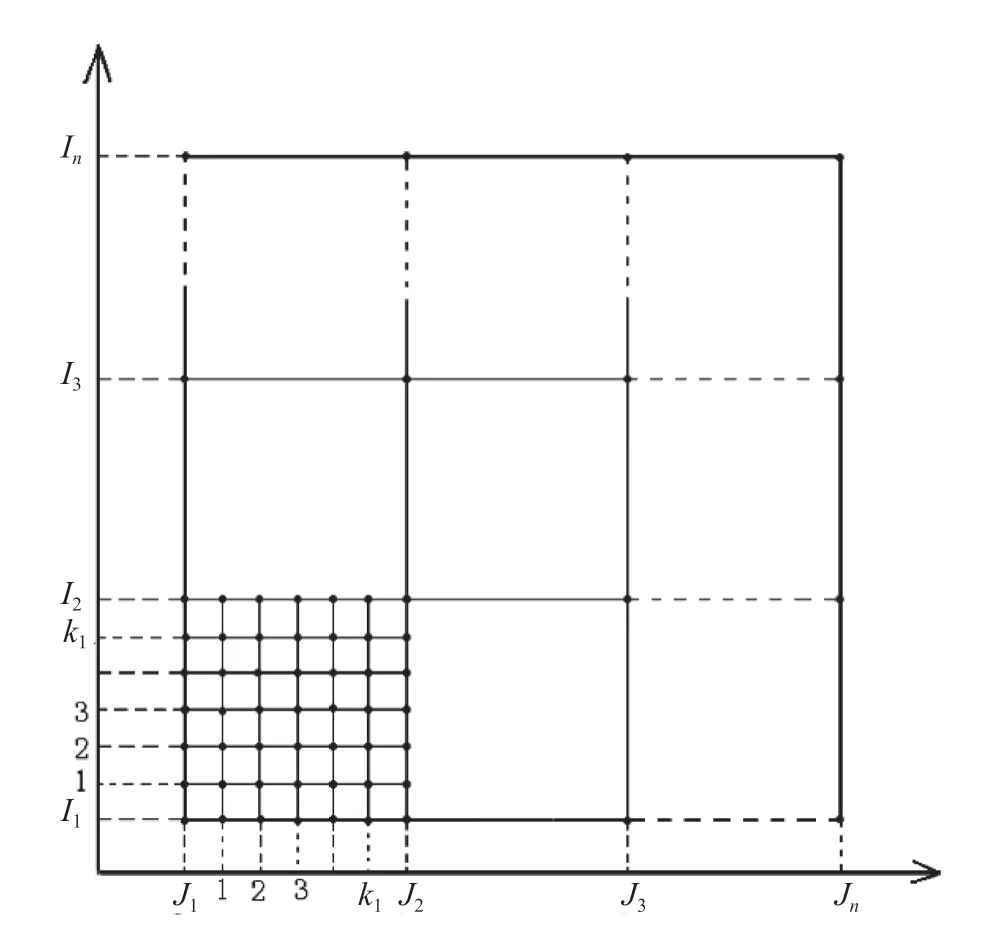
圖1 氣動網格離散示意圖

Jn代表數據塊中J列第n個壓力點，In代表數據塊中I行第n個壓力點，k1代表在每一行（列）相鄰的2個點之間的空間直線上等距離增加k1個點，以k表示k1個點中任意一個點，即k＝1，2，3，....，k1，如圖1所示，每個增加點對應的數值信息的計算方法如公式（1）～公式（8）所示。

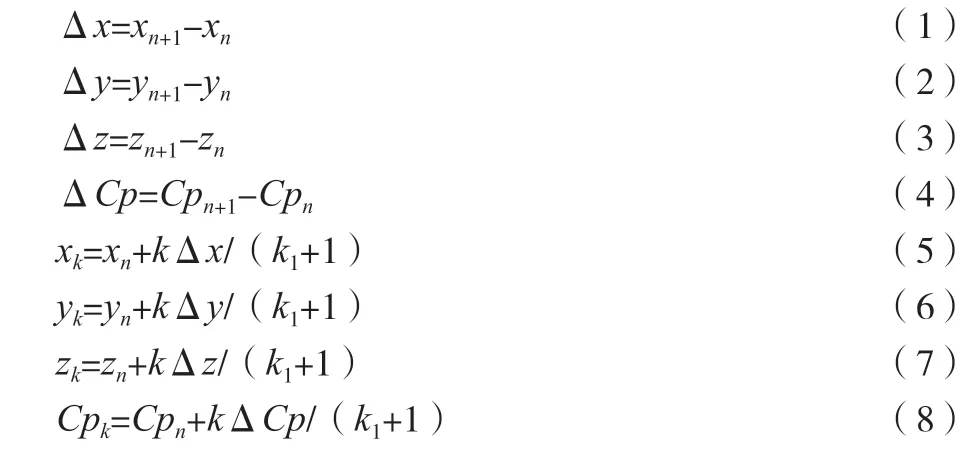
式中：xn、yn和zn為第n個壓力點的坐標；xn+1、yn+1和zn+1為第n+1個壓力點的坐標；xk、yk和zk為第k個壓力點坐標；k為插值點編號；Cpn為第n個壓力點的壓力系數；Cpn+1為第n+1個壓力點的壓力系數。

以In點為起始，位置坐標每增加（Δx、Δy、Δz）/（k1+1），壓力系數就增加ΔCp/（k1+1），直至In+1點，組成了一個In點到In+1的等差值數列，共k1+2個點，每兩個點的坐標、壓力系數差值為（Δx、Δy、Δz、ΔCp）/（k1+1）。

每行的點按上述離散方法進行離散，得到了一個全新的二維數組。列的加密和行的加密一樣，可以將加密后的I行J列數組看成一個J行I列的數組，依舊對行進行離散得到最終的數組。上述CFD數據加密方法的核心是認為行（列）相鄰點的壓力系數是線性分布的，從而進行線性加密，為下一步計算做好準備。

1.5 等效到有限元模型

需要關注的有限元模型提供的信息包括每個網格的組成節點、每個節點的坐標。每個網格的組成節點信息關系到最后結果的輸出格式（與該文無關，不再贅述）。每個節點的坐標信息是下一步計算的關鍵信息，任意節點記為節點k，坐標表述為（xk、yk、zk）。

求解任意節點坐標（xk、yk、zk）和離散后的每個壓力點坐標（xc、yc、zc）的空間距離L，如公式（9）所示。

該處遵循的是編程的循環邏輯，給出判斷標準距離L1，如果某一個壓力點和有限元節點的距離L≤L1，那么就將壓力點對應的壓力賦值到有限元節點上，依次循環，直到找出最小距離對應的壓力點。

完成上述步驟后，該文的核心算法就已經完成，可以描述為首先對CFD數據進行線性加密；其次，根據空間距離判斷，將距離任意有限元節點空間最近的CFD數據網格點的壓力系數賦值到有限元節點上。

2 驗證

上述計算方法很容易編寫成程序，為了驗證程序的可靠性和該方法的可行性，使用程序對飛機的整流罩氣動載荷進行分配，將分配結果與某數據處理軟件的處理結果進行對比，部分壓力點的對比如圖2所示，應力云圖如圖3和圖4所示，合力對比見表4。

表4 整流罩氣動載荷合力

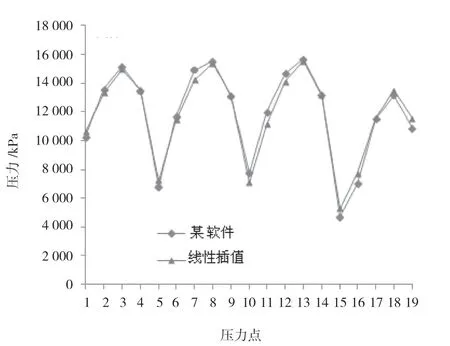
圖2 部分壓力點壓力

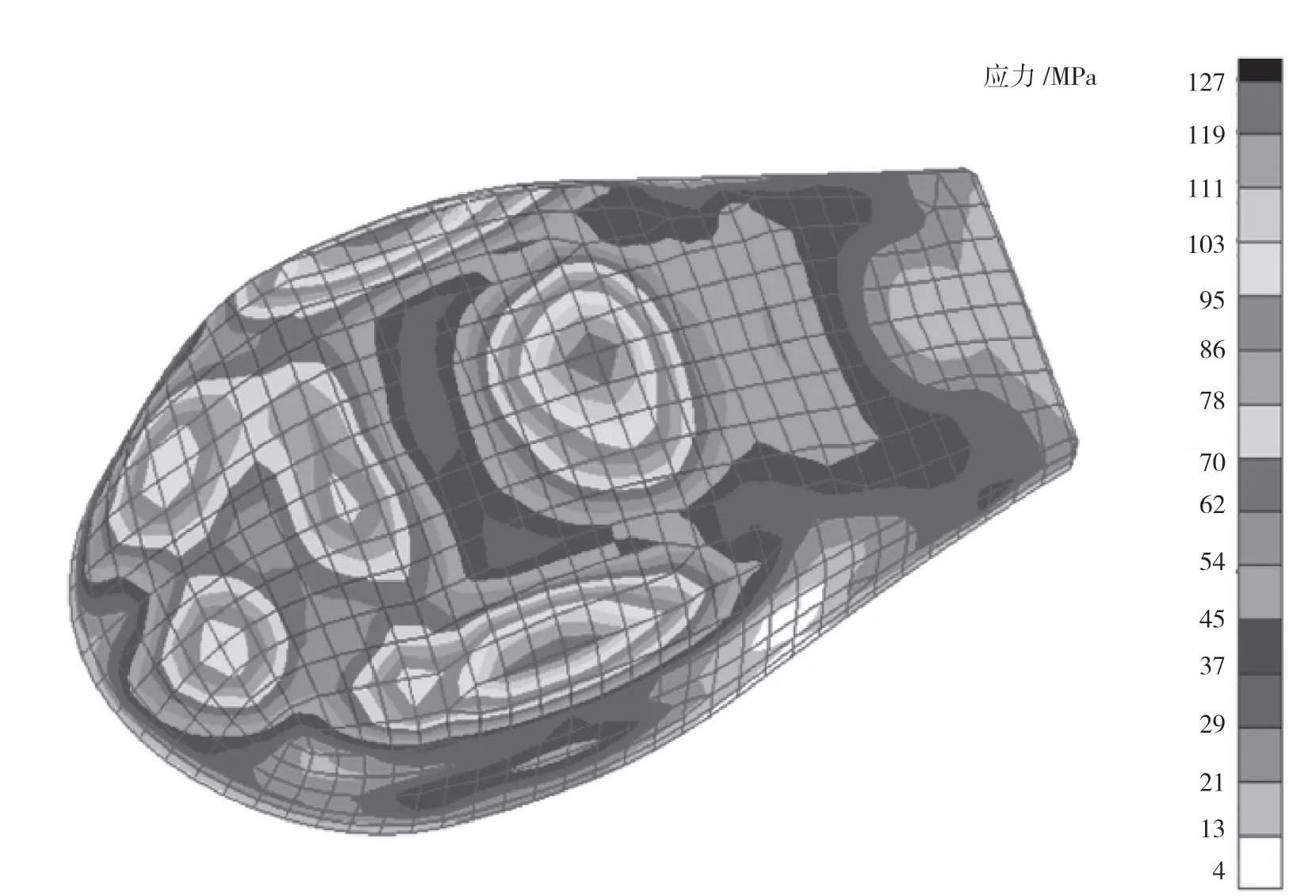
圖3 線性插值應力云圖

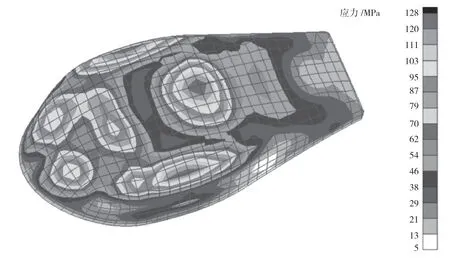
圖4 某軟件應力云圖

從上述結果可以得出：2種載荷分配方法的單點壓力平均誤差約為4%，應力分布云圖基本一致，主要力素合力誤差約為3%，近似滿足靜力等效、分布等效原則。

3 結論

對該文研究的氣動載荷分配方法進行程序化處理后，可以處理整流罩各種常用的壓力分布數值或風洞測壓氣動數據，輸出各CAE分析工具能夠讀取的載荷數據，且通用性較好，可以方便、快捷地用于類似整流罩結構的氣動載荷分配，具有一定的工程實用價值。

但同時也面臨一個問題，該方法只解決了整流罩強度分析所需要的載荷，后期還需要根據情況對整流罩罩強度試驗加載載荷劃分加載區域，將其轉化為集中力，方便人為地對其進行不斷迭代處理，下一步需要不斷完善，從而實現試驗加載載荷程序的功能。