風、浪荷載作用下海上風機單樁結構灌漿連接段疲勞性能評價

黎亞舟，王 銜, ，陳 濤，顧祥林

(1. 中交第三航務工程局有限公司，上海 200032；2. 同濟大學 工程結構服役性能演化與控制教育部重點實驗室，上海 200092)

單樁支撐結構作為最為流行的海上風電基礎形式，截止2019年，單樁結構形式占整個歐洲所有已裝機的海上風電基礎的81%[1]。單樁與上部結構連接主要的手段是灌漿連接，其技術的原理是通過在內外鋼管間的環形間隙中填充高性能灌漿料的方式來連接直徑不同的過渡段和鋼管樁。隨著7～10 MW級風電機組技術的發展，風機葉輪半徑和重量的增加對基礎支撐結構安全性能提出了更高的要求。海上風電支撐結構在20年使用壽命期間需承受高達109次風、浪荷載作用[2]，因此其疲勞性能尤為重要。

灌漿連接段最早的應用出現在20世紀70年代海洋石油燃氣平臺導管架結構中，當時的學者對灌漿連接段的軸向靜力極限承載力的關注遠高于疲勞性能，同時期只有少數學者[3-6]關注灌漿連接的軸向疲勞強度。這里以單樁支撐結構作為研究對象，其灌漿連接段主要受到彎矩作用，軸向荷載變化較小。對于灌漿連接段的彎曲疲勞性能，近20年來許多學者也進行了相關的試驗研究[7-9]，并依據相關試驗結果對灌漿連接段設計規范[10]進行了相關修訂。

基于385種工況下的廣東某實際5 MW單樁風機支撐結構在風、浪荷載作用下的動力響應分析，獲取了灌漿連接段荷載邊界條件時程。建立灌漿連接段精細化有限元子模型，將荷載邊界條件轉化為應力時程。對于剪力鍵采用“熱點應力”方法進行疲勞性能評價。對于灌漿材料，選取剪力鍵附近灌漿材料單元積分點處的第三主應力進行疲勞性能評價。采用Palmgren-Miner線性損傷累計準則和雨流計數方法進行疲勞損傷的累計。

1 某實際5 MW單樁支撐結構在風、浪荷載作用下的動力響應

圖1給出了某5 MW海上風機單樁結構示意圖及實地場地條件，其主要設計參數如表1所示。結合廣東省某地一年內的實際風、浪實測數據，運用譜表達法模擬生成了385種工況下單樁風機結構上的隨機風、浪荷載時程，主要包括風機運行氣動荷載、風機塔身風荷載、波浪荷載。為簡化計算，較為保守地將所有荷載作用在同一平面內。

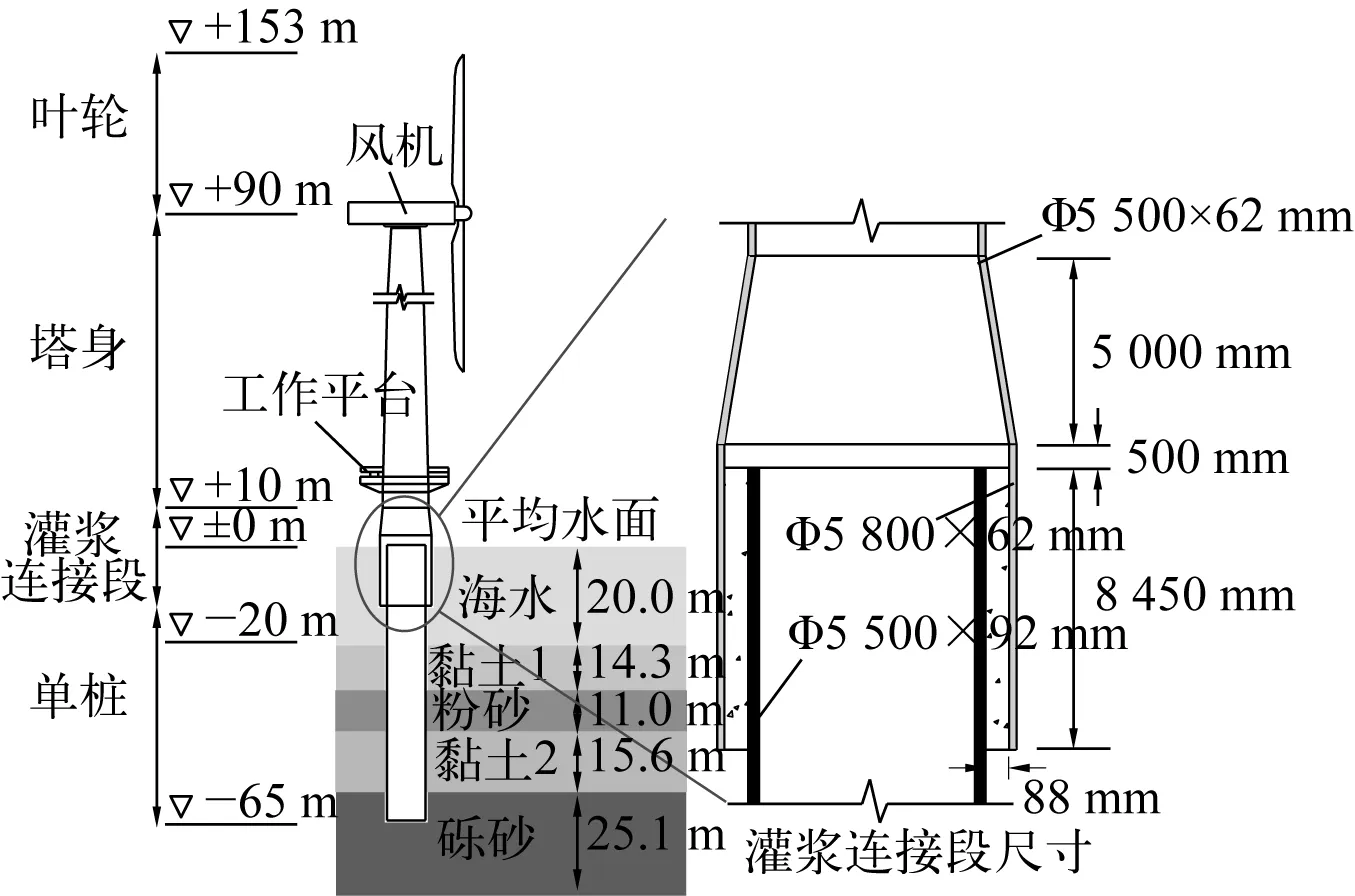
圖1 某實際5 MW單樁支撐結構及實際場地條件Fig. 1 Real 5 MW monopile structure and soil condition

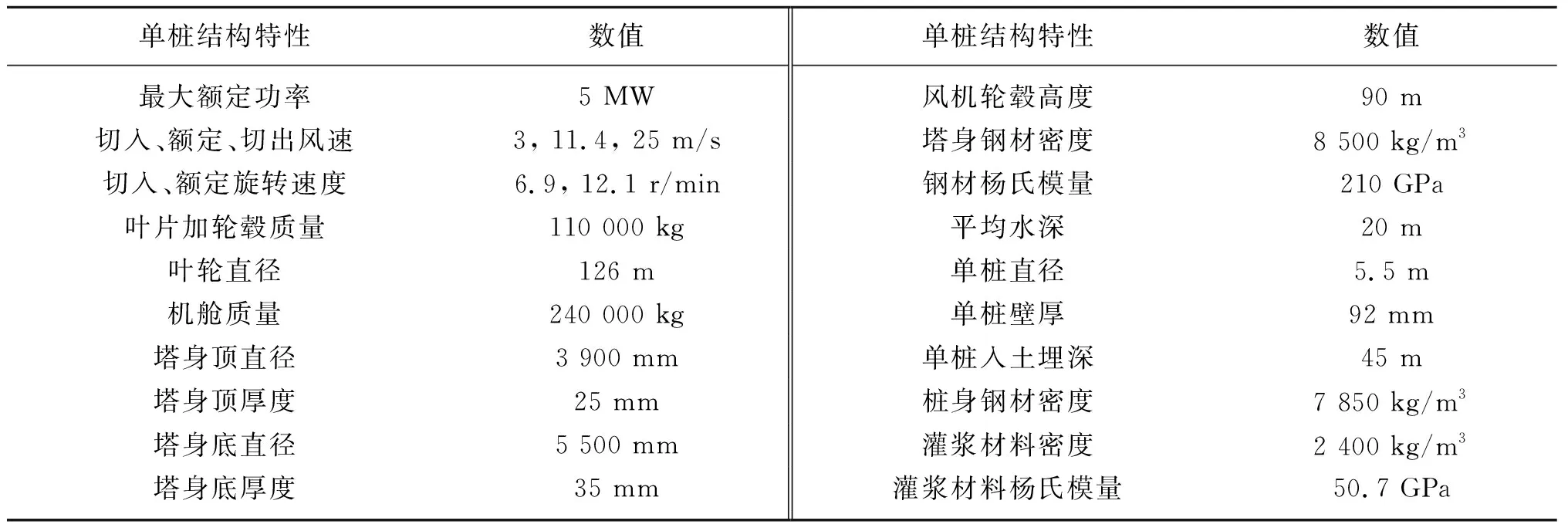
表1 某實際5 MW海上風機單樁結構設計參數

建立了綜合考慮樁—土相互作用、灌漿連接段影響以及多種工況下不同阻尼比的實際單樁支撐結構的動力響應模型。實現了385種風浪耦合工況下的單樁支撐結構的時域動力響應分析及灌漿連接段的荷載邊界條件時程的提取，如圖2所示。此部分在文獻[17]中敘述，文中不再詳述。

圖2 單樁支撐結構動力分析及荷載邊界條件提取Fig. 2 Dynamic analysis and load boundaries extraction

2 某實際灌漿連接段精細化有限元模型

采用Abaqus軟件進行建模，建立的灌漿連接段精細化有限元模型如圖3所示，詳細的建模方法可參見文獻[18]。該模型采用導管架灌漿連接段軸壓試驗以及單樁結構灌漿連接段疲勞后軸向靜力試驗的相關結果進行了驗證，詳見文獻[19]，在此都不再贅述。通過此精細化有限元模型可將灌漿連接段的荷載邊界條件時程轉化為應力的時程。

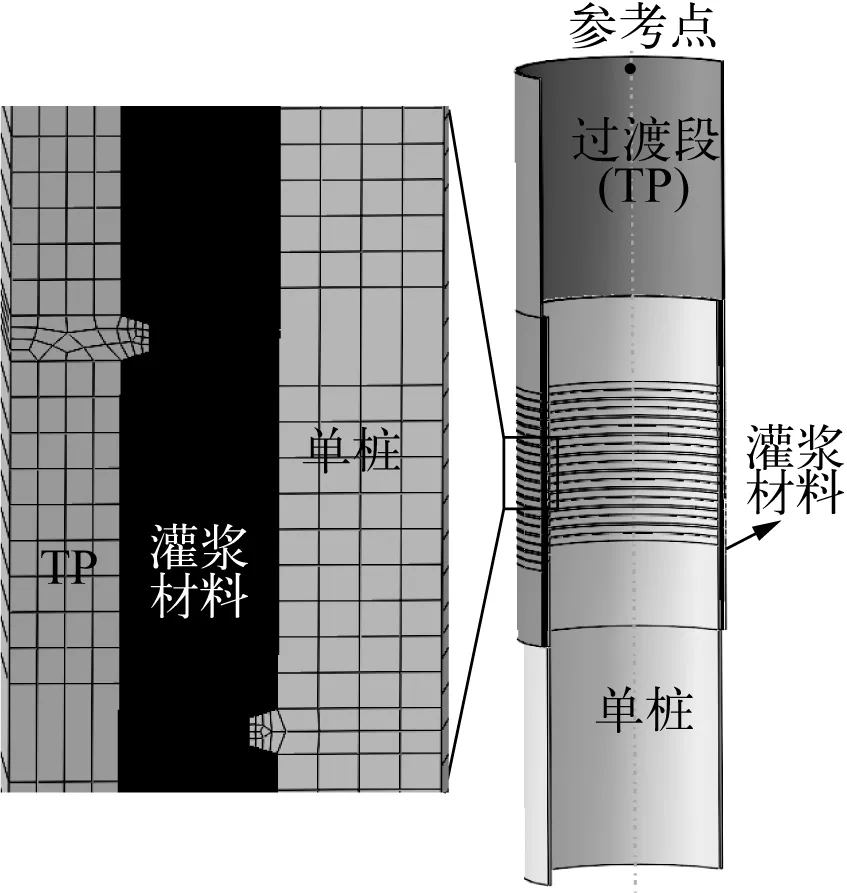
圖3 灌漿連接段精細化有限元模型Fig. 3 Refined finite element models for grouted

按照圖1中尺寸建立某實際單樁風機結構中灌漿連接段有限元模型。其中剪力鍵布置在灌漿連接段中間1/2長度內，間距s=450 mm，剪力鍵高度h=16 mm，剪力鍵寬度w=26 mm。剪力鍵的編號如圖4所示。鋼管和灌漿材料的材料屬性取某次材性試驗的實測值，如表2所示。

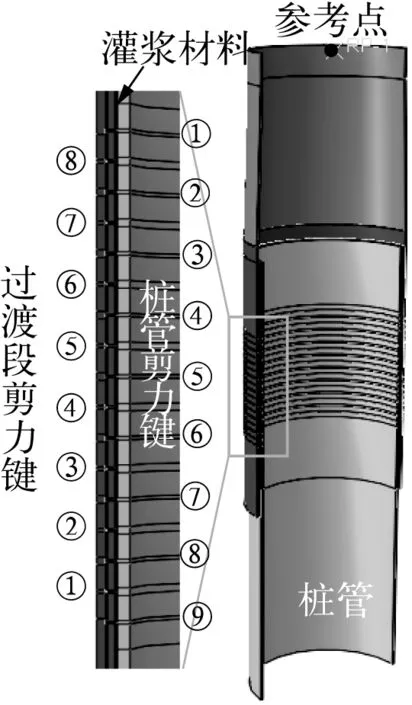
圖4 某實際灌漿段內剪力鍵編號Fig. 4 The numbers of shear keys in the real grouted connection

表2 某實際灌漿連接段材料性能參數

3 灌漿連接段疲勞性能評價方式

灌漿連接段是由鋼結構和灌漿材料組成的組合結構，故其疲勞性能評價應當分成鋼結構、灌漿材料兩部分敘述。本節將從這兩方面介紹灌漿連接段性能的評價方式，并補充介紹DNVGL-ST-0126規范[20]提出的建立在其承載力理論公式基礎上的灌漿連接段整體結構疲勞性能評價方式。

3.1 Palmgren-Miner線性損傷累計準則

Palmgren-Miner線性損傷累計準則是疲勞分析中最常見的損傷累計方法，其假定所有k種工況下的結構或構件的總損傷值D是每種工況下損傷值的累加之和，即：

(1)

其中，ni是第i種工況出現的次數，可采用文獻[21]附錄A中所述方法對數據進行過濾，并通過雨流計數法進行統計，相關介紹可參見文獻[22-23]，雨流計數法采用的是美國材料與試驗協會(ASTM)標準“E 1049-85”[24]中5.4.4節規定的；Ni是第i種工況下的疲勞壽命。一般假定構件或結構的總損傷值D低于某一特定限值時就不會發生疲勞破壞。

3.2 焊接剪力鍵的疲勞性能

灌漿連接段內通常可能出現鋼材疲勞破壞的位置為焊接剪力鍵附近，因此，采用“熱點應力”法預估此灌漿連接段內鋼管焊接剪力鍵的疲勞壽命。不同規范對于“熱點應力”的計算方式定義一般略有差異，采用DNVGL-RP-C203[25]建立焊縫處的幾何有限元模型，取出距離焊趾0.5t和1.5t(t為焊接母材厚度)位置處的“幾何應力”，通過線性插值即可得到焊趾處的“熱點應力”。

如圖5所示，平行焊縫方向的正應力可用σP表示，平行于焊縫方向的剪應力可用τP表示，而垂直于焊縫方向的正應力可用σV表示；圖中“Δ”符號代表應力分量的變化值即應力幅。距離焊趾位置0.5t和1.5t處“幾何應力”的應力幅可按下式計算：

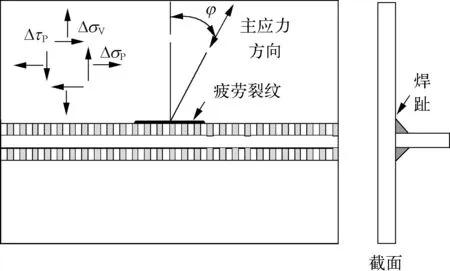
圖5 焊縫應力的示意Fig. 5 Stress components around the welded toes

(2)

其中，Δσ1表示焊縫平面內最大主應力幅，表示Δσ2焊縫平面內最小主應力幅，則有：

(3)

(4)

參數α的取值，規范[25]附錄表A-3詳細規定了焊縫的分類方法和等級評定，當考慮剪力鍵焊縫為手工焊縫這種最不利情況時，參數α取為0.90。

得到上述距離剪力鍵焊趾0.5t及1.5t處的應力分量后進行線性插值，即可以得到焊趾處(即0t處)的應力分量，計算所有應力分量的變化幅度，根據式(2)計算焊趾處的“幾何應力”(即“熱點應力”)的應力幅Δσeff_0t。

得到焊趾處的“熱點應力”的應力幅Δσeff_0t后，根據規范[25]的2.4.3節相關規定，若考慮焊接母材厚度的影響，則鋼管焊接剪力鍵的疲勞壽命與“熱點應力”的應力幅之間的關系可以用式(5)的S-N曲線表示。

(5)

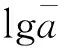
同時，規范[25]中規定，當焊接結構無法監測及維修時，式(1)中的總損傷值D的限值為1/3。

3.3 灌漿材料的疲勞性能

DNVGL海上混凝土結構設計規范DNVGL-ST-C502[26]中給出的混凝土或灌漿材料的S-N曲線，其表達式如式(6)所示。

(6)

式中：frd為材料破壞時的抗壓強度；C1為參數，在空氣中的結構取為12.0；水中受壓—壓循環時取為10.0，受拉—壓循環時取8.0。

(7)

式中：γm為材料分項系數，對有剪力鍵灌漿連接段疲勞分析時取為1.5；fcn為灌漿材料場地的抗壓強度，按式(8)計算。

(8)

其中，fcck為灌漿材料抗壓強度代表值，由150 mm直徑，300 mm高度圓柱體試塊測得；σmax為應力循環中的最大壓應力；σmin為應力循環中的最小壓應力，當為拉應力時取為0；C5為疲勞強度參數，對混凝土可取為1.0，對灌漿材料需要通過試驗確定，當無試驗時取為0.8。

如果式(6)計算所得的lgN大于式(9)中X值，則此計算值須乘以式(10)中參數C2。

(9)

C2=[1+0.2(lgN-X)]>1.0

(10)

與焊接結構的規定類似，規范[26]中也規定當焊接結構無法監測及維修時，式(1)中的總損傷值D的限值為1/3。

由于剪力鍵局部區域存在較為嚴重應力集中，灌漿連接段中的灌漿材料的裂紋一般始于剪力鍵位置。因此，將灌漿材料的疲勞性能計算位置定在如圖6所示的剪力鍵局部區域上方和下方的單元；利用單元積分點的第三主應力和上述灌漿材料的S-N曲線評價灌漿層的疲勞壽命。

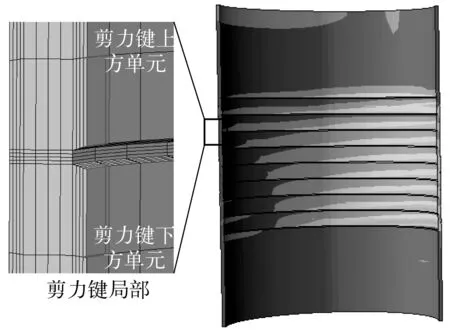
圖6 有限元模型灌漿層剪力鍵區域計算疲勞性能位置Fig. 6 Location for calculation of fatigue property of grout material

3.4 灌漿連接段的整體疲勞性能

DNVGL-ST-0126規范[20]給出了灌漿連接段的整體疲勞性能分析方法，該方法建立在其推導的灌漿連接段承載力理論公式[8,27]基礎上，定義y為某一荷載循環下，單位長度的單層剪力鍵上所受荷載FV1Shk和剪力鍵承載力設計值FV1Shk, cap的比值，即

(11)

式中：γm為材料參數，對有剪力鍵灌漿連接段疲勞分析時取為1.5。

則在此荷載循環下灌漿連接段的疲勞壽命N為

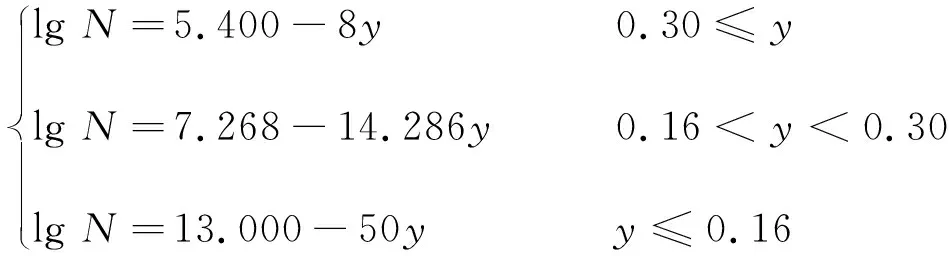
(12)

然而該疲勞壽命曲線只建立在有限的試驗數據基礎上并且保守地取為試驗數據的下包線，無法準確預測灌漿連接段疲勞壽命，后文的計算結果將進一步說明該曲線的保守性。

4 風、浪荷載作用下灌漿連接段疲勞性能評價

4.1 灌漿連接段荷載邊界條件的簡化

經過對提取的灌漿連接段實際荷載邊界條件進行統計，頂部軸力FV1最大值為6 472.6 kN，最小值為6 469.6 kN，變化范圍很小，同樣底部軸力FV2最大值為8 525.7 kN，最小值為8 522.4 kN。因此可將軸力簡化為固定值，取頂部軸力FV1為6 475 kN。采用圖4所示的半模型，頂部軸力值為3 237.5 kN，忽略灌漿連接段上部過渡段鋼管的重量，保守地將該軸力直接施加在半模型頂部的參考點上。

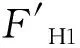
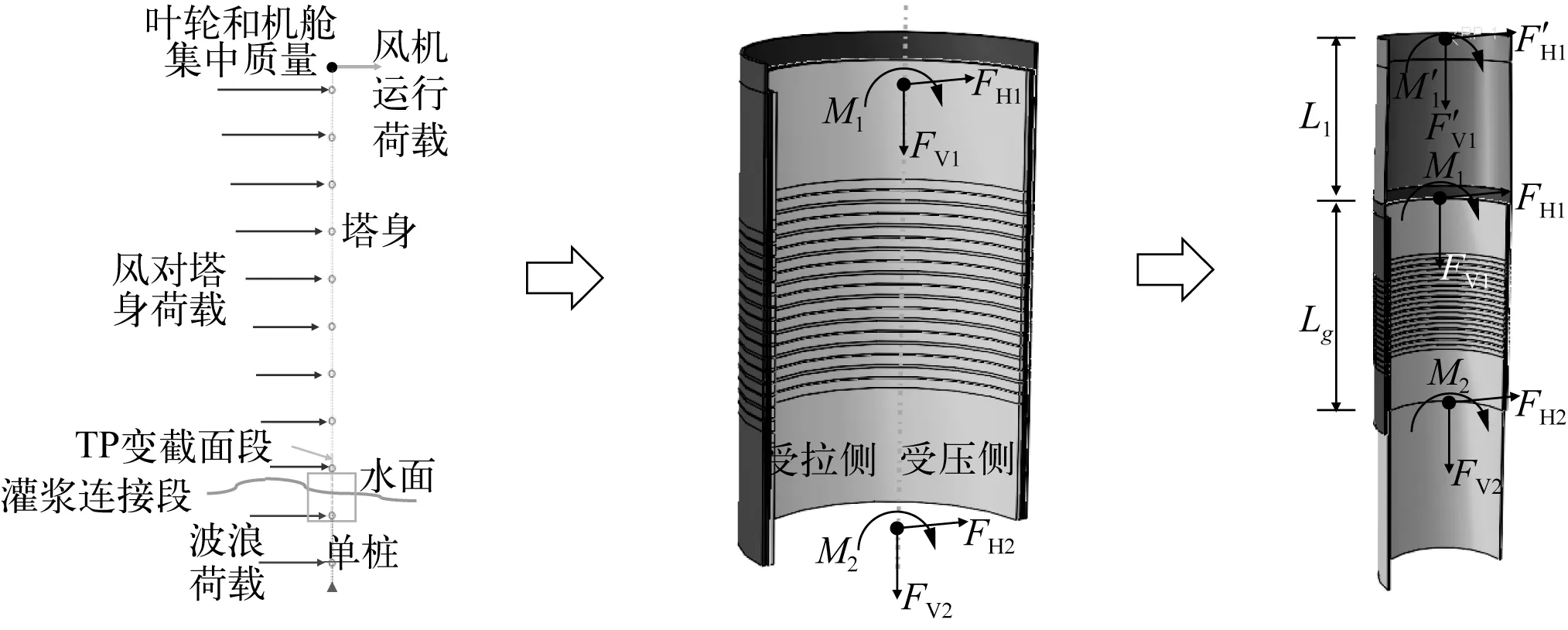
圖7 灌漿連接段邊界條件的簡化Fig. 7 Simplification of the load boundary conditions

(13)

(14)

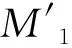
4.2 灌漿連接段精細化有限元模型確定應力分布

4.2.1 彎矩和水平力作用下的應力疊加

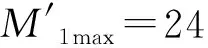
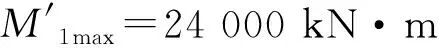
在最大彎矩荷載和水平力同時作用下樁管的最大Mises應力出現在圖4中的⑨號剪力鍵處，最大值為49.89 MPa，仍處于彈性狀態。過渡段鋼管的最大Mises應力出現在圖4的⑧號剪力鍵處，最大值為75.99 MPa，也處于彈性狀態。灌漿材料第三主應力最大值出現在樁管側⑧號剪力鍵附近，最大值為25.27 MPa，小于最大受壓強度87.6 MPa的1/3，處于彈性狀態。由于所有部件仍處于材料的彈性階段，因此可以考慮進行彎矩荷載和水平力分別作用下的疊加。

對三種工況下的應力狀態最大值位置的應力進行提取，如表3所示。

表3 某實際灌漿連接段材料性能參數

將三種工況下的樁管、過渡段、灌漿材料的最大應力值分別減去軸力和自重作用下的應力值，以彎矩和水平力共同作用下的工況作為基準，利用彎矩和水平力分別作用時兩種工況的加和減去基準值后，再除以基準值，可得到彎矩和水平力分別作用下的最大應力直接疊加產生的誤差。從表3中可知，除去重力和軸力荷載后，灌漿材料和樁管內部最大應力值直接疊加的誤差均在2%左右，而過渡段內部最大應力直接疊加的誤差也僅在8.5%以內。同時，由于三種工況是所有彎矩和水平荷載的最大包絡值，由此可以認為在此范圍內的隨機彎矩和水平力荷載作用下的應力狀態可以進行疊加。

4.2.2 彎矩和水平力單獨作用下的應力分量的提取

通過Abaqus后處理文件，分別提取除去重力和軸力荷載后，彎矩或水平力單獨作用下灌漿連接段內部的應力分量與荷載大小間的關系。由于假定水平力和彎矩荷載都只作用在灌漿連接段的對稱面上，因此應力最大的截面必然出現在對稱面上，因而只需考慮對稱面上的應力分量即可。

對于鋼管上的焊接剪力鍵，如圖8所示，按照3.2節所述的方法計算熱點應力時，需要距離焊趾0.5t和1.5t位置的應力分量，即同時提取圖8中剪力鍵焊趾上方和下方的②號、③號、⑦號和⑧號節點的應力分量，從而插值得到所需位置的應力分量。

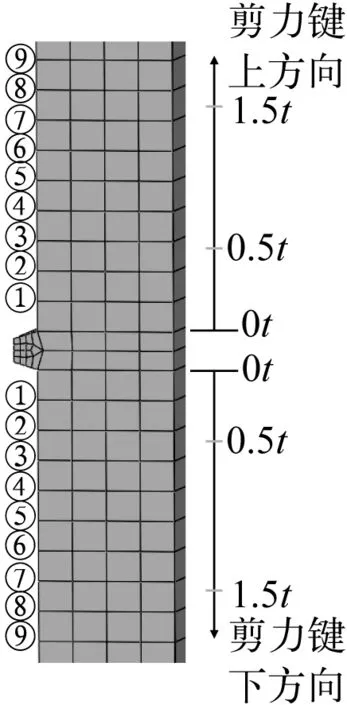
圖8 剪力鍵局部網格及應力分量提取 Fig. 8 Stress components extraction around the shear key

對于灌漿材料，如3.3節所述，提取剪力鍵上方和下方最外層單元積分點處的第三主應力分量。

考慮到灌漿連接段內剪力鍵數量較多，且需提取不同荷載水平下的應力分量，因此利用Python語言編寫Abaqus后處理程序，分別提取水平力和彎矩荷載分別作用下，灌漿連接段內剪力鍵附近鋼管應力分量和灌漿材料第三主應力隨荷載值變化的情況。

4.3 焊接剪力鍵疲勞性能評估

結合已經得到的灌漿連接段的荷載邊界條件時程，以及除去重力和軸力荷載后，水平力和彎矩荷載單獨作用下灌漿連接段內剪力鍵局部鋼管應力分量與荷載值的關系；編寫Matlab程序，通過荷載和應力的關系插值，轉化為距焊趾0.5t和1.5t位置的應力分量時程。最后通過線性插值，得到鋼管剪力鍵焊趾處熱點應力分量的時程。

值得注意的是，3.2節所述的焊接剪力鍵疲勞性能“熱點應力”評價方法相關計算時只考慮應力分量的變化幅值，而無需考慮應力分量的平均值，因此無需考慮重力和軸力荷載對應力分量平均值的影響，可直接采用除去重力和軸力荷載后的應力分量時程。

假定焊接剪力鍵為手工焊接，考慮水中并有陰極保護的S-N曲線，并將數據過濾的幅度定為“熱點應力”應力幅Δσeff_0t的1/200。若某種工況下焊趾處的損傷值為di，其持續的時間為ti，發生的概率Pi，若假定海上風機單樁支撐結構的使用壽命T為20年，則依據線性損傷累計方法，某一剪力鍵位置處的總損傷D為各種工況下損傷Di的疊加：

(15)

經過計算后所有剪力鍵的最大損傷值D為1.349 8×10-10，出現在圖4中過渡段受壓側最上方的⑧號剪力鍵上方焊趾處。此損傷值遠小于3.2節規定的限值1/3，證明灌漿連接段在假設的20年的使用壽命中，焊接剪力鍵焊趾處不會發生疲勞破壞。

4.4 灌漿材料疲勞性能評估

與焊接剪力鍵疲勞性能評估思路類似，編寫相應的Matlab程序，通過荷載和應力的關系插值，將荷載邊界條件時程轉化為剪力鍵局部灌漿材料第三主應力分量時程。

值得注意的是，與焊接剪力鍵疲勞損傷計算不同，3.3節的灌漿材料的S-N曲線相關計算時同時考慮應力分量最大值和最小值，因此需要考慮重力和軸力荷載對應力分量平均值的影響。讀取重力和軸力荷載下的應力分量，直接疊加在彎矩和水平力荷載時程計算得到的應力分量時程上。

假定灌漿材料圓柱體單軸抗壓強度為實測值87.56 MPa，并且參數C5取為0.85；材料分項系數取為1.5；在水中但只有壓—壓循環，則式(6)中參數C1取為10。同樣，將Markov過濾的幅度定為應力分量幅度的1/200，經過式(15)計算后所有剪力鍵附近的灌漿材料的最大損傷值D為0.001 54，出現在圖4中過渡段受壓側最上方的⑧號剪力鍵下方處，此損傷值大于焊接剪力鍵的最大損傷值，證明灌漿連接段在風、浪疲勞荷載下，灌漿材料疲勞起控制作用。然而灌漿材料損傷值D依舊在2‰之內，遠小于3.3節規定的限值1/3，即在假設的20年的使用壽命中，灌漿連接段不會發生破壞。

分析上述所有工況下，起控制作用的過渡段受壓側最上方的⑧號剪力鍵下方灌漿材料的損傷值Di，取出排名前十的工況，如表4所示。從表中可知，前十位的工況風速均為12 m/s，此時風速最接近于5 MW風機運行的額定風速11.4 m/s，風機以額定風速運行時產生的推力最大。將損傷值Di前五位的工況的風、浪功率譜以及單樁風機結構基頻都進行標準化處理后，繪制在圖9中。從圖中可知，Kaimal風譜峰值仍距離風機結構基頻較遠；而產生損傷值Di較大的前兩種工況的B-M海浪譜的峰值也并非最為靠近結構基頻，反而排名第三的Hs=1.25 m，Ts=5.005 s的工況的峰值頻率更加接近結構基頻，因此得出如下結論:海浪譜的峰值頻率與結構基頻越接近并不會對灌漿連接段產生越大的損傷值。

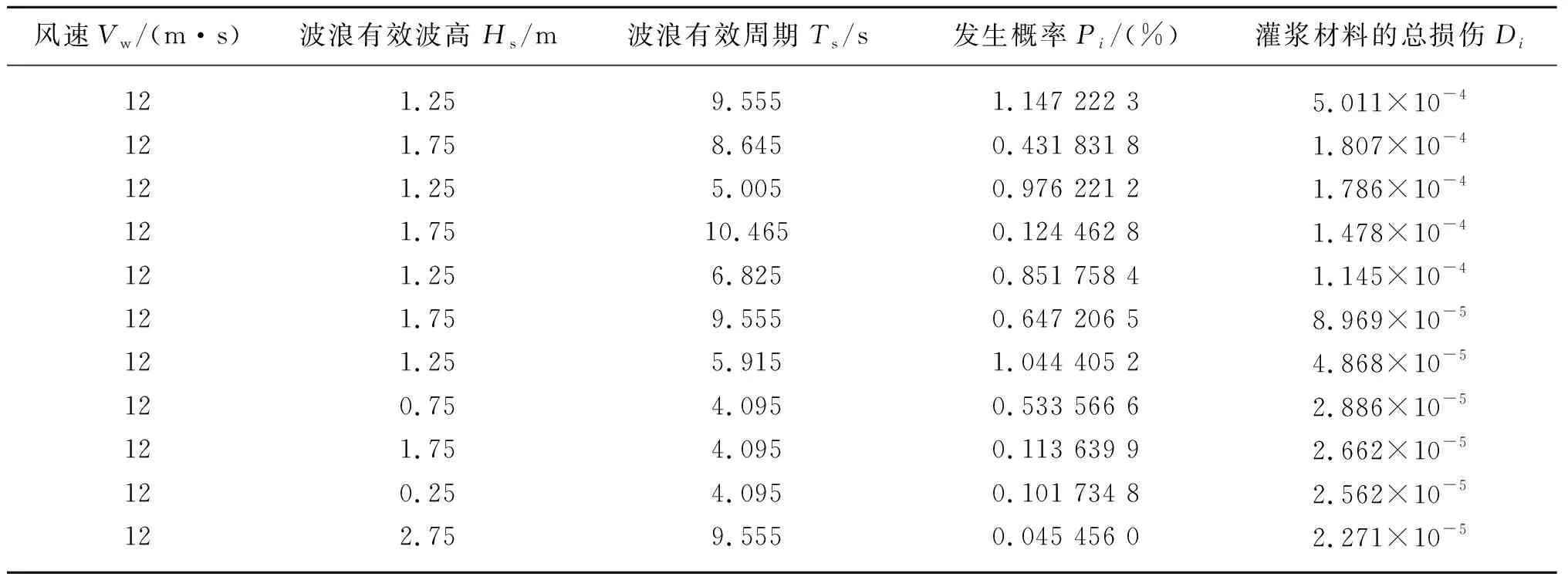
表4 過渡段受壓側最上方的⑧號剪力鍵下方灌漿材料損傷Di前十位的工況

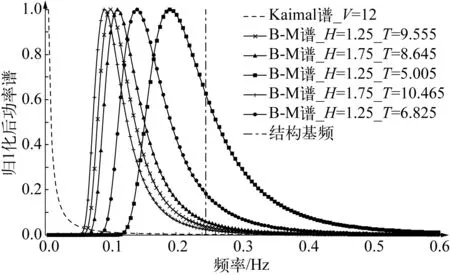
圖9 灌漿材料損傷Di的前五位不同工況下風 、浪荷載譜和結構基頻的關系Fig. 9 Wind and wave spectrum under the 5 load conditions with the largest damage values

4.5 灌漿連接段整體疲勞性能評價

依據3.4節中所述的DNVGL-ST-0126規范[20]對灌漿連接段整體疲勞性能的評價方法，進行了相關計算。

假定設計中采用的灌漿材料75 mm立方體抗壓強度為130 MPa；鋼材楊氏模量為206 GP，泊松比為0.3；灌漿材料楊氏模量為50 GPa。將數據過濾的幅度定為式(11)中y值的1/200，則經過計算后發現，排名前9的工況損傷值Di都大于1，總損傷值D更是達到38.62。說明按照3.4節所述的規范[20]對灌漿連接段整體疲勞性能的評價方法計算，灌漿連接段早已發生破壞。然而，4.3節和4.4節的相關計算證明灌漿連接段的總損傷值僅在2‰之內，由此證明規范[20]中方法的保守性，按此規范進行灌漿連接段的疲勞設計可能會造成不必要的浪費。

5 結 語

灌漿連接段的疲勞性能對于海上風機單樁支撐結構至關重要。基于385種工況下的廣東某實際5 MW單樁風機支撐結構在風、浪荷載作用下的動力響應分析，獲取了灌漿連接段荷載邊界條件時程。建立灌漿連接段精細化有限元子模型，將荷載邊界條件轉化為應力時程。由此對風、浪荷載作用下的灌漿連接段進行了疲勞性能評價，得到了如下結論：

1) 對焊接剪力鍵焊趾附近應力分量時程進行“熱點應力”法相關計算，得到在假定的海上風機20年的使用壽命中，損傷最大的剪力鍵的總損傷D為1.349 8×10-10。

2) 對剪力鍵附近灌漿材料的第三主應力時程進行相關計算，得到在假定的海上風機20年的使用壽命中，損傷最大的剪力鍵附近的灌漿材料總損傷D為1.54×10-3。由此可見，灌漿連接段的疲勞性能由灌漿材料控制。由于損傷值遠小于限值1/3，也說明在現有的荷載條件下，灌漿連接段在20年的使用壽命中不會發生破壞。

3) 分析產生損傷較大的前幾種工況進行可知，風速為12 m/s時，最接近5 MW標準風機的額定風速，此時風機運行對單樁結構的推力最大，產生的疲勞損傷也最大；同時海浪譜的峰值頻率與結構基頻越接近并不會對灌漿連接段產生越大的損傷值。

4) 采用DNVGL-ST-0126規范[20]的相關方法，對灌漿連接段整體疲勞性能進行了評價。經過相關程序計算，發現產生損傷值較大的前9種工況的Di都遠大于1，總損傷值D更是達到38.62；與1)和2)條結果比較，說明了規范[20]的整體疲勞性能評價方法的過分保守性。

文中所提出的對于風、浪荷載作用下的單樁基礎灌漿連接段的疲勞性能評價方法是具有較好地普適性的，可以推廣到其他結構形式中的灌漿連接段中。然而，計算中目前僅有一年的實際場地風、浪實測數據，用該數據推測海上風機單樁支撐結構灌漿連接段的疲勞性能可能不具有代表性，未來的工作中應采用更加豐富而全面的數據進行分析。