最優覆蓋校內巡邏車配備方案及其評估模型

王澤松，王梓天，萬后鵬，秦澤青

（1.湖北大學計算機與信息工程學院，武漢430062；2.湖北工業大學計算機學院，武漢430062）

1 問題分析

我們以某校為例，考慮該校的實際情況，同時假設該校突發事故發生現場均在圖1的道路上。該校三個重點部位的坐標分別為：（5112，4806）、（9126，4266）、（7434，1332）（見圖1紅點部位，藍色部分為水域，相鄰兩個交叉路口之間的道路近似認為是直線）。

圖1 數據生成全景圖

該校擬增加一批配有先進通訊設備的校園巡邏車。假設學校內校園巡邏車的平均速度為15Km/h，遇到緊急事故開往事故現場的平均速度為30Km/h。校園巡邏車配備及巡邏方案要盡量滿足以下要求：

D1：校園巡邏車在接到校園報警電話后四分鐘之內趕到現場的不低于90%；而趕到重點部位的時間必須在三分鐘之內。

D2：使巡邏效果更顯著。

現需要建立數學模型解決以下問題：

（1）若要求滿足D1，該校最少需配備多少輛校園巡邏車？

（2）請給出評價巡邏效果的評價指標，并給出滿足D1且盡量滿足D2條件的校園巡邏方案。

（3）你認為還有哪些因素、哪些情況需要考慮？給出相應的解決方案。

對于如何求在滿足D1條件時，校園所需配備巡邏車的最少數量，我們可先將路口與道路信息從坐標軸中提出，轉化為帶權無向圖結構，用節點表示路口，邊表示道路，各邊權重則代表著道路的長度。針對要求D1，我們通過時間與巡邏車速度的信息，將對時間的限制變成了對距離的限制，從而，問題一的概念發生了如圖2的改變。

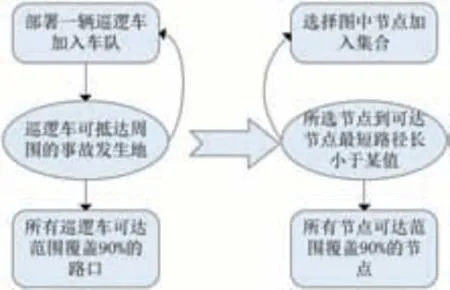
圖2 概念轉化圖

接下來，我們所需解決的，也就是“找到最少節點集，其可達覆蓋至少90%的節點”的問題。為了使巡邏效果更顯著結合我們對巡邏車在實際工作中工作方式的理解，在巡邏效果的評估上，我們給出三個參考因素。

（1）整體覆蓋率

我們認為首先應該提及的就是巡邏車隊整體的作用覆蓋率。這是由于巡邏路徑對整體作用范圍的影響是直觀的，故整體的覆蓋率可以直接體現一套巡邏方案中，策劃者對巡邏路徑所作安排的優劣。

（2）應答時效

鑒于事件的發生方式完全隨機，我們優先考慮極端情況，即突發事件發生時，巡邏車到達事發地點所需行駛的距離達到巡邏路徑上的最大值，并將此時巡邏車趕到事發地點的用時記作應答時效tmax，我們認為該數值可以反映巡邏方案對極端緊急情形的應對能力。

（3）巡邏路徑長度

基于節能環保，倡導綠色生活的宗旨，我們希望在滿足需求的情況下，巡邏車消耗最少的電量，即行駛最短的距離，因此，將巡邏路徑的總長度納入考慮因素，其可以反映巡邏方案在節能上的作用效果。在三項參考因素的基礎上，我們根據各因素的重要性為其分配權值，并融合得到評分指標γ。

2 模型的假設

根據本文提出的問題和以上的問題分析，我們做了如下模型假設：

（1）在問題一中，假設巡邏車的位置均位于交叉路口。

（2）在問題一中，假設重點部位等不在道路上的點近似到最近的交叉路口及道路上。

（3）在問題一中，經計算，圖中兩交叉路口間連線距離小于2000m的概率為99%（4分鐘內均可到達），故假設面積覆蓋率等價于交叉路口的覆蓋率。

（4）在問題二中，假設巡邏車在處理事故時耗費時間為無窮大，且事件總并發數小于等于巡邏車數量。即巡邏車到達事件處理地點后不可移動，僅能解決當前位置的事故。

（5）在問題二中，對于巡邏車路徑的移動我們假設在同類型的區域內從一個交叉路口移動到另一個交叉路口的時間相同，且由于不同區域之間距離較遠，從效率角度假設巡邏車不會跨區域進行巡邏。

3 符號說明

本文常用符號見下表，其他符號見文中說明。

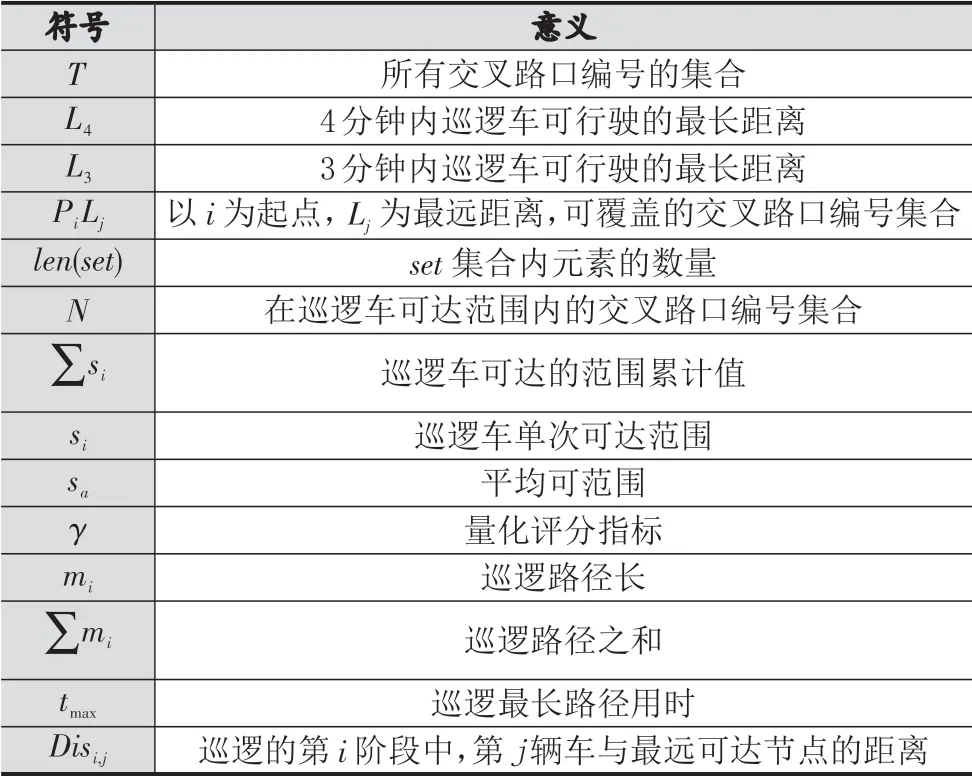
表1

4 模型的建立與求解

文獻[1]中利用了退火算法進行路徑優化調度，文獻[2]基于博弈論對巡邏策略展開了研究。不同于它們，本文采用蒙特卡洛算法進行模擬巡邏軌跡，并結合圖論算法達到模型的自優化效果。

4.1 問題一的建模與求解

問題一中需要求出滿足D1條件時，需要部署的最少巡邏車數目，為解決該問題，我們使用蒙特卡洛法與弗洛伊德法，建立了最小消耗覆蓋模型。本小節的主要內容是最小消耗覆蓋模型的建立、模型的求解與分析、問題一的回答。

（1）最小消耗覆蓋模型的建立

本模型主要采取了“覆蓋”的思想，通過將路口與道路信息轉化為圖，進而把4分鐘內“趕到現場不低于90%”轉化為“4分鐘內巡邏車活動覆蓋面積大于校園的90%”。在求解最小巡邏車數目的過程中，利用蒙特卡洛模擬算法來隨機模擬巡邏車的初始位置，再通過使用弗洛伊德算法求出任意兩節點間的最短路徑，可以得到每輛巡邏車可覆蓋的面積，經由假設3，巡邏車可達面積的覆蓋率可等價于巡邏車可達交叉路口的覆蓋率，單次蒙特卡洛模擬的簡化流程如圖3所示。

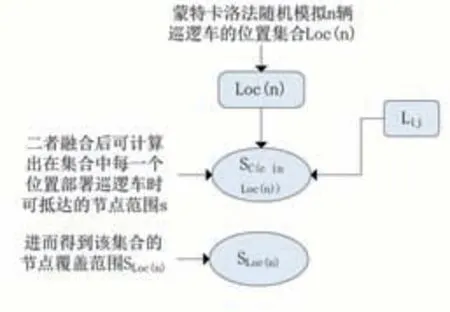
圖3 單次蒙特卡洛模擬的簡化流程

蒙特卡洛算法在大規模的隨機數列與復雜系統中的模擬有著杰出的表現，例如在電力系統中的評估[3-4]、水質概率預報[5]、證券定價[6]，等等。因此，我們認為其模擬的巡邏車初始位置與真實環境具有高度相似性。

在蒙特卡洛模擬過程中，為得到最小且符合要求的巡邏車數len(N)，我們還需要加上約束條件：

①四分鐘之內趕到現場的不低于90%：

以4分鐘內巡邏車可以行駛的距離為度量指標，利用弗洛伊德算法計算每輛巡邏車可以覆蓋的交叉路口數，使覆蓋總數大于交叉路口數的90%。

②重點部位的時間必須在三分鐘之內趕到：

以三個重點部位為圓心，以內巡邏車可以行駛的距離為度量指標。分別計算三分鐘內可以到達這三點的交叉路口集合，最終巡邏車的位置應該包含這些集合中的點。

（2）模型的求解與分析

①計算方法的設計

在求解最小消耗覆蓋模型時，我們首先將約束條件轉換為公式表達：

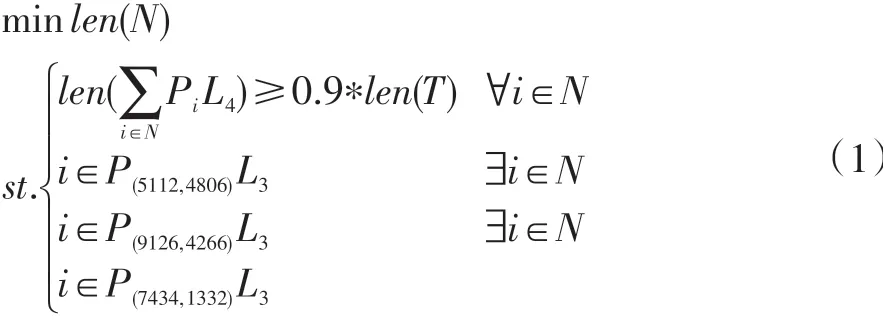
基于建模過程中提到的單次蒙特卡洛模擬，我們將其結合弗洛伊德算法，應用在圖結構上，并寫出完整算法，如圖4所示。

圖4 問題一算法流程圖

單輛巡邏車的覆蓋范圍的計算如表2所示。

表2 單車輛覆蓋范圍示例

由于約束條件的存在，我們需要針對三個重點檢測地進行特別處理，從3分鐘內可覆蓋它們的節點中進行單獨選取，以保證模擬的巡邏車位置能滿足條件，及時趕到重點地點。可及時抵達三處重點檢測地的節點編號集合如表3所示。

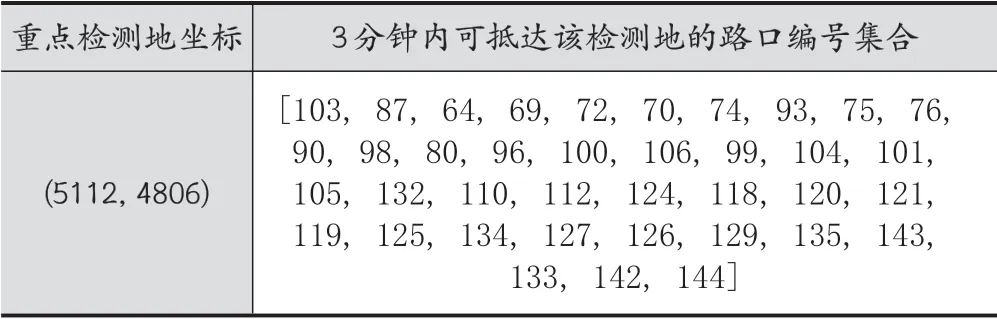
表3 可及時抵達重點檢測地的路口編號集

續表

②結果分析

最終，所用車輛最少時，巡邏車所在交叉路口的編號分別為[140，94，40，290，137，261，217，49，12，260，250，25，105，213，180，43，300，10，305，116，8]。此時蒙特卡洛模擬結果如圖5所示。圖中，紅色的點代表巡邏車所在的位置，紅色加綠色是緊急情況發生4分鐘內能覆蓋到的范圍，由圖可見，21輛巡邏車的覆蓋范圍大于90%，且可在3分鐘內前往重點地段。

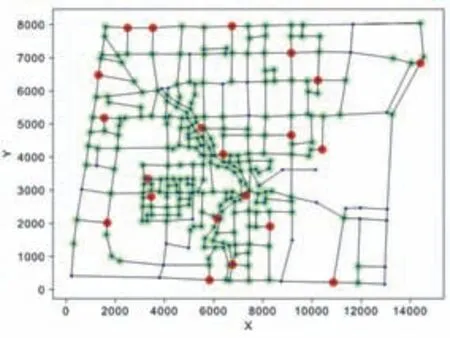
圖5 最終蒙特卡洛模擬結果

③問題一的回答

經計算得出，滿足要求D1時，該校最少需配備21輛校園巡邏車。

4.2 問題二的建模與求解

問題二要求給出評價巡邏效果的評價指標，并給出效果顯著的巡邏方案。結合我們對問題二的分析中提出的影響因素，我們建立CTL模型來幫助我們評價巡邏效果，進而計算出一個可供方案間比較的評分數值，擇出分數最高的巡邏方案進行選用。本小節的主要內容為CTL模型的建立、模型的求解與分析、問題二的回答。

（1）CTL模型的建立

在問題二的分析中我們已經提到需要考慮的三個影響因素，C（整體覆蓋率）、T（應答時效）、L（巡邏路徑長度），在它們的基礎上，我們構建CTL模型來對巡邏方案進行評估，求解評分數值γ。

下面給出C、T、L的定義與推導：

C：整體覆蓋率

根據不同點間平均路徑的差異，我們將巡邏點分為不同的區域。基于假設5，我們可知相同區域內巡邏車是同時移動的。每當所有巡邏車到達新的交叉路口時，記錄下當前的三分鐘內所有巡邏車可達位置的范圍si，取多次范圍si求和。

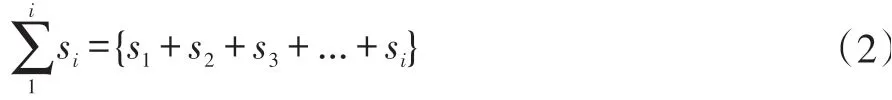
利用∑1i s i，對巡邏方案中不同階段的s i求均值得到該巡邏方案的平均覆蓋范圍s a，同時對于巡邏車的位置進行多次重置，回到起始點，且巡邏車每次從相距自身最近的三個交叉路口中選擇一個作為下次訪問的路口，保證計算的范圍具有普適性。

我們用區域里覆蓋范圍內交叉路口數除以本區域內所有路口數Ta作為整體覆蓋率。

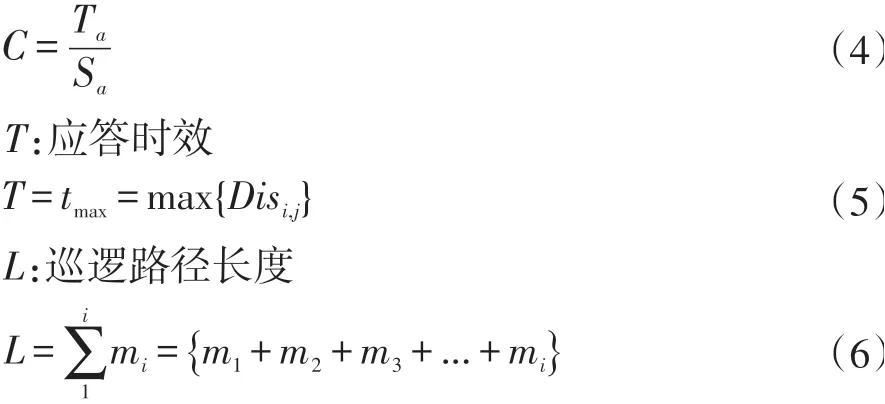
為找出三種因素中的在評價過程中的重要性關系，我們利用AHP層次分析法對這三項指標進行分析，進而得到定量的評價指標γ。

在擁有評價指標后，我們繼續使用蒙特卡洛模擬不同的巡邏方案，從中選擇覆蓋率高于90%，且γ值最小的方案。

（2）模型的求解與分析

依據節點間平均距離的差異，我們將地圖分為兩塊區域，如圖6所示。區域1代表低密度區域，也就是正方形區域，區域二代表高密度區域，也就是三角形區域。

在對三項指標進行AHP分析之后，得到的判斷矩陣如下：

對矩陣進行一致性檢驗，我們得到了指標情況CR<0.10，所以該判斷矩陣A的一致性可以接受，同時我們使用算術平均法求得權重。

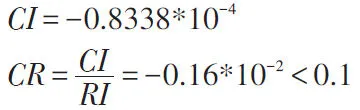
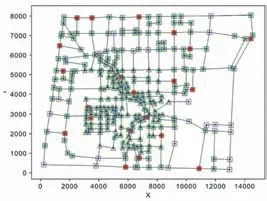
圖6 分區

根據計算的結果，我們得到定量的評價指標如下：

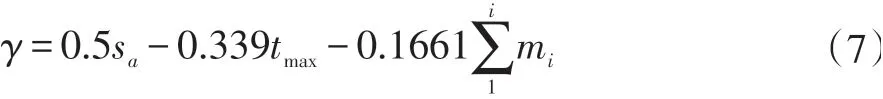
將各參數的值進行歸一化后代入計算我們就能得到量化的巡邏效果評價指標。

我們利用蒙特卡洛法進行了1000000次隨機模擬，每次巡邏車隨機移動至與當前路口相鄰的路口，我們控制每個區域里的覆蓋率大于90%，且γ值最小，計算出了最佳巡邏方案，在最佳方案下，兩區域的評分與覆蓋率如表4所示。

表4 計算結果

（3）問題二的回答

我們使用經由CTL模型生成的γ作為方案評價指標，并給出在此指標下表現最優的方案。

4.3 問題二的分析與求解

在前兩問的分析中，我們認為巡邏車處理事件的用時為無窮大，由此避免了某一巡邏階段中，單巡邏車處理了多個突發事件的情形發生；同時我們也假設了，事件總并發數不超過巡邏車數目，且僅會發生一次，解決后不再復發，從而將情況控制在了巡邏車可處理范圍內。然而在實際維護治安的過程中，處理治安事件的時間不一定為無窮大，往往巡邏車趕到目標地點后，僅花費短暫時間即可解決事件并離開；事件并發數目也不總是如我們所愿，以至于巡邏車能輕而易舉地擺平校園內的所有突發事件。

（1）對于不同用時事件進行分類處理

在考慮到巡邏車處理用時不總為無限長后，我們對事件的類型進行分類分析，對于少部分處理事件所需時間為無窮的事件，我們采用之前的分配方案，同時對于在短時內可以處理的事件我們則需對其進行新的優化處理。

為了便于分析，我們假設事件分為兩種，一種事件處理時間為無限長，巡邏車到達事件發生地點后無法移動。第二種事件處理事件為無限短，即認為巡邏車到達后事件即解決，巡邏車可立即前往一下事發地點。同時我們認為不同類型的事件發生時應存在某種特定比例。

我們用以下的情形來模擬：

車輛總數不變記為n，并發事件數q等于車輛總數也為n，當事件并發時每次出現的處理時間無限長事件數ql占全部事件數的一半，當總數為奇數時，ql向下取整。全部事件解決后車輛重新分布規劃，隨后發生新一次事件并發。我們意圖展現出在事件過量發生時整個系統具備的穩健性，我們記錄下每一次并發后所有事件解決的總范圍并要求在問題1的要求下的總巡邏范圍至少要達到總面積的60%，并以此分析出在車輛不足場景下巡邏軌跡以及巡邏點的生成規律是否受到影響。

（2）對于高事件并發數情形的應對

在前兩問的背景下，事件發生的次數我們認為不超過巡邏車輛數，并且再一次發生后事件不再更新。實際上事故可能會不斷發生，于是我們認為事故每隔一段時間會繼續發生，直至超過巡邏車可以處理的最大值。由于事件的并發數的失控，我們需要容錯率更高的部署方案，因此，巡邏車不再只部署在各交叉路口，將其轉移到事故多發地的中心加以應對，如此，巡邏車在解決事件后可迅速趕往下一處事件發生地。

我們首先將所有事件發生地點進行聚類，把各簇中心視作事件發生地。同時由于簇中心數顯著小于車輛總數，車輛可根據簇的密度前往各聚類中心。每當一次事件解決完成后，重新進行一次聚類過程直至所有的事件決完成。相較于前兩問的情況，此情況下事件發生的位置處于動態變化之中，需要對車輛的運動過程進行實時的分析。鑒于我們單次并發產生的事件數較少，經多次實驗，我們發現使用Mean-Shift算法可以得到最好的聚類效果。我們以輪廓系數作為標準評價幾種分類算法，輪廓系數定義如下：

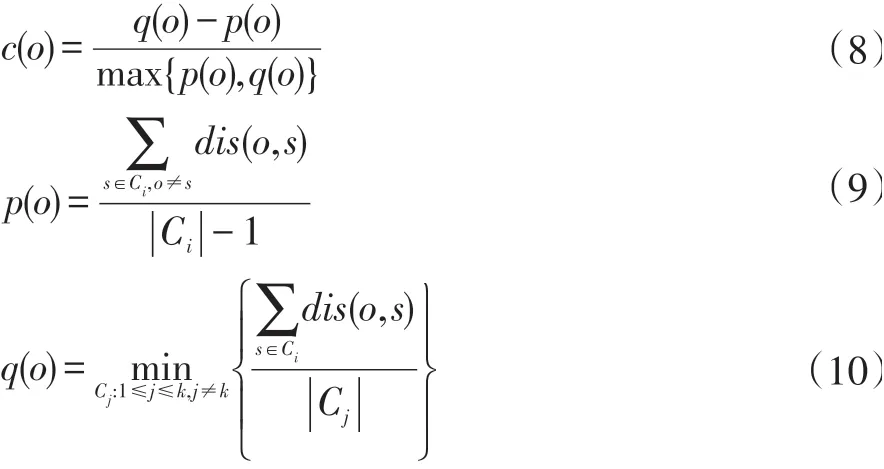
式中：

O代表C i中的對象，p（o）代表o與C i中剩余對象的均值，q（o）代表o與Ci中其他點的平均距離，c（o）代表O的輪廓系數。

最終公式如下：

各聚類方法效果如表5所示。

表5 各聚類方法效果

5 模型的評價與推廣

5.1 模型的優點

針對問題1：

我們結合了蒙特卡洛模擬和圖論中的弗洛伊德算法，用蒙特卡洛算法模擬巡邏車的初始位置與數量，以弗洛伊德算法求得的最短路徑為指標計算巡邏車在不同時間段內可覆蓋的最大范圍。最終生成了巡邏覆蓋圖清晰且直觀地展現了采取本策略可達到的預期成效。

針對問題2：

由于在實際的巡邏過程中，車輛處于運動狀態。我們選取了整體覆蓋率、應答時效和巡邏路徑這三個方面作為優化巡邏路線的三個評價指標并采取了層次分析法對其進行了附權。我們依照路口密度將校園進行了分區并求解最優，最終校園百分之九十以上的路段都會被巡邏到，發生緊急情況時可做到全覆蓋。

針對問題3：

為了設計出更符合實際場景的巡邏過程，我們將巡邏過程進行了兩方面的擴充，首先將巡邏處理的事件種類做了擴充，此外還考慮了事件并發的重復過程，使得整個模擬環境由靜態轉為動態。最終我們發現在這樣一個動態模擬的環境下，需要優先對生成的數據進行聚類分析，經多次實驗我們找到了聚類效果最好的Mean-Shift算法，實現了動態分析最優巡邏路徑。

5.2 模型的缺點

針對問題1：

部分路口之間的距離大于2000，在求覆蓋率時忽略了這些細微因素的影響，直接用交叉路口的覆蓋率代替了面積覆蓋率。

針對問題2：

層次分析法附權帶有稍許主觀色彩，在有真實數據支撐的情況下可以用熵權法來修訂參數。

針對問題3：

由于事件并發數數量的限制，聚類算法分析結果的可靠性有待提升。

5.3 模型的推廣

本模型可用來指定校園巡邏策略，可以通過圖的形式清晰直觀地展示成效。同時隨著評價體系的建立，本模型可對校園已經采取的巡邏策略進行評估，便于后期的改進。同時本模型還考慮了在處理事件類型不同且事件多次并發情況下的巡邏路徑分析策略，可為不同的事件提供不同的方案，通過在不同條件下及時進行對路徑的調整得到最佳的動態巡邏策略。