潛艇應急上浮機動不穩定性建模與仿真*

呂幫俊，陳 佳，黃 斌，彭利坤

（海軍工程大學動力工程學院，武漢 430033）

0 引言

潛艇在水下遭遇火災或艙室進水，需要快速上浮至水面狀態。一般的操縱方法是，用尾升降舵造成一定的尾傾，增加螺旋槳的轉速，同時吹除主壓載水艙使潛艇快速上浮到水面。如果潛艇上浮時躍出水面，浮心將會迅速下移，此時上層建筑內的水尚來不及排出導致重心下移滯后，因此，將會造成潛艇的短時失穩，倘若潛艇在浮至水面狀態之前已經形成了比較大的橫傾，浮至水面后極易形成危險橫傾［1］。Itard 通過自航模試驗觀察到“枯葉”現象，潛艇上浮最大橫傾角可達到60°［2］。戴余良等采用奇異性與分叉理論，分析了潛艇在左右舷對稱的情況下，應急上浮運動并不限于垂直面內，可能出現橫滾，在某種臨界條件下，該運動可能失穩而出現分叉現象［3］。Watt 等認為潛艇應急上浮過程中，造成橫傾失穩，最關鍵的因素是指揮臺圍殼受到非對稱流動的影響［4］。如何在潛艇設計階段針對此強非線性機動過程的潛艇運動狀態進行準確預報，是避免出現上浮橫搖甚至失穩問題的核心和關鍵。

從潛艇的設計和安全航行的角度出發，需要能夠精確預報潛艇在各種戰術機動，或者應急機動時的運動狀態變化情況。在應急吹除過程中，需要對極端非穩態機動過程進行計算仿真。目前有多種手段可用于潛艇應急浮起過程的運動狀態預報，自航模試驗方法是全尺度機動預報最有效的方法［4］。然而，進行這些測試與試驗，一方面需要高額的費用，另一方面，相當一部分試驗由于其高風險性，在很多國家的海軍是被禁止的。此外，由于試驗條件限制，很多試驗達不到實艇實尺度所能達到的雷諾數，尺度效應的問題不能得到有效解決。

計算機仿真提供了成本相對較低的研究方法，主要包括兩類：一類是采用計算流體力學軟件，模擬實艇或縮比模型在水中的運動，如CFD 流體計算軟件，可以同時輸出各種流動特征參數，包括壓力，速度，渦流強度，切應力，紊流程度，等［5］。分析這些流動特征可以對該問題的物理過程提供深度視角，而試驗方法中，無法得到這些細節，尤其是非穩態機動過程中測量流動區域的相關參數非常困難。另一類是采用潛艇六自由度運動微分方程和水動力模型試驗結果，進行潛艇運動仿真求解和操縱性能預報，該方法最早由Gertler 和Hagen 在1967 年提出［6］，并由Feldman 在1979 年進行了修正［7］。運動方程中的水動力和力矩都是潛艇運動狀態參數及其微分的函數，并采用一定階數的泰勒展開進行近似和簡化。由于泰勒展開式中，各項的形式都是運動參數乘以定常的水動力系數，因此，該方法也被稱為基于水動力系數的仿真方法。Feldman 修正的模型考慮了潛艇在高速大舵角回轉運動中橫向流的影響及水平面運動過程中的水動力非線性，運動過程中水動力產生的歷程效應，但該運動模型，基于來流攻角小于18°的水動力試驗數據，因此，該模型僅適用于潛艇常規操縱時的性能預報［8］。Park 等采用高階多項式，分別對潛艇大攻角拖曳水池和風洞試驗結果進行曲面擬合，取得了較高的吻合度，該模型適用于潛艇高速回轉以及應急上浮大攻角機動時的運動預報［9］。劉輝等結合大攻角及螺旋槳變負荷拘束船模水動力試驗，采用潛艇大攻角應急挽回操縱模型，較好地預報了潛艇艙室進水時成功挽回能力和運動規律［10］。

隨著現代潛艇朝著大潛深、高航速的方向發展，尤其是戰術訓練中往往需要潛艇在垂直面以高航速、大攻角作強機動，上述機動過程中，水動力的非線性、不對稱性和耦合特性，使得潛艇的空間機動呈現高維復雜非線性特征，也是目前潛艇操縱控制和運動預報領域研究的重點和難點。區別于傳統的基于攻角和漂角定義下的潛艇操縱運動水動力描述形式［11］，本文采用了潛艇大攻角操縱運動數學模型，分別結合高壓氣吹除指數模型和拉瓦爾噴管模型，對潛艇高壓氣吹除應急上浮過程的運動狀態進行了預報，并重點研究了應急上浮過程橫傾角的影響因素，為制定科學安全的潛艇應急上浮策略提供解決方案。

1 潛艇大攻角操縱運動數學模型

圖1 描述潛艇空間機動的坐標系

2 穩定性判據

為了給出大攻角強機動工況下潛艇的橫搖穩定性判據，基于上述大攻角操縱運動數學模型中的橫搖力矩方程式（4），可以得到單自由度準靜態穩定性指標［4］

3 高壓氣吹除主壓載水艙模型

高壓氣吹除主壓載水艙數學模型是進行高壓氣吹除計算最便捷而有效的手段，文獻［4］采用了指數模型對高壓氣吹除過程進行了計算，并進一步對吹除后潛艇的運動狀態進行了預報。然而，指數模型沒有考慮排水孔面積以及水艙外背壓變化等因素的影響，計算結果存在一定誤差，因此，本文將采用更為準確的拉瓦爾噴管模型［15］對高壓氣吹除過程進行計算。在此，分別給出指數模型和拉瓦爾噴管模型，用于計算和比較不同吹除模型對潛艇上浮狀態預報結果的差異。

3.1 指數吹除模型

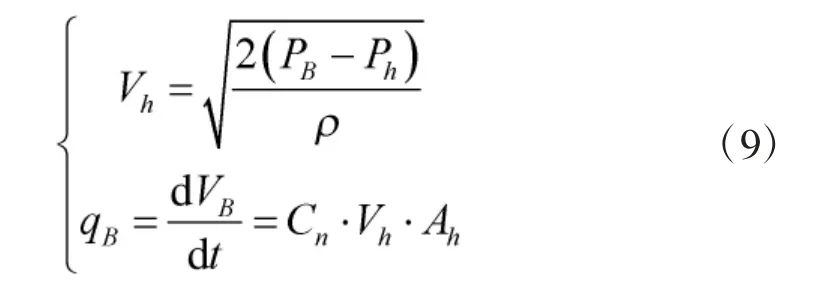
3.2 拉瓦爾噴管模型

瑞典國家哥德堡船模試驗池Bystrom 基于拉瓦爾噴管理論，分3 部分給出了高壓氣吹除主壓載水艙數學模型［15］，成為潛艇高壓氣吹除系統計算的理論基礎。

壓載水艙的排水模型

壓載水艙的壓力變化模型

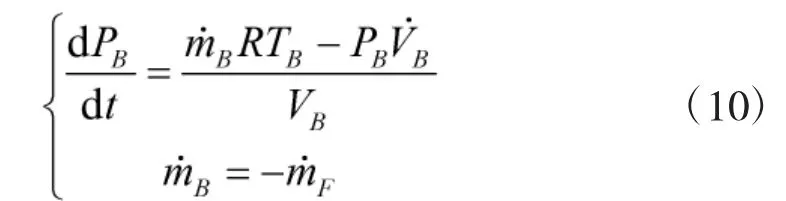
氣瓶釋放氣體流量模型

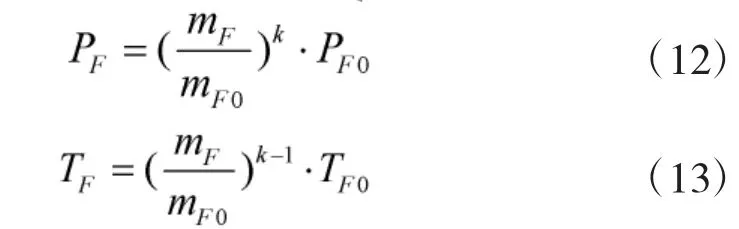
式中，Ph為壓載水艙的舷外瞬時壓力，ρ 為海水密度，Cn為損耗系數，Vh為排水速度，Ah為水艙排水孔面積，m˙F為高壓氣流量，At為噴嘴的噴口面積；Ct為閥流量系數（0≤Ct≤1），k 為等熵常數，R 為氣體常數，PF0為氣瓶中的初始壓力，mF0為氣瓶中初始質量；TF0為氣瓶初始溫度。

軟件各模塊組成如圖3 所示，其中，初始化模塊用于設定潛艇的初始航速、深度、縱橫傾角、選取的吹除模型以及水艙吹除順序、吹除延時等，高壓氣吹除模塊分別按照3.1、3.2 中的相關理論計算高壓氣吹除過程的各參數，潛艇大攻角運動模型解算模塊為整個軟件的核心，采用四階龍格庫塔數值積分算法求解潛艇操縱運動參數，并將潛艇運動參數及水艙水量、高壓氣壓力變化等狀態參數存儲為excel 表格，用于Matlab 調用進行作圖分析。

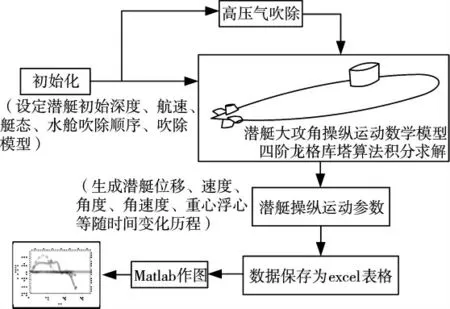
圖3 潛艇高壓氣吹除應急上浮機動仿真分析軟件組成

4 仿真平臺搭建

為了開展潛艇應急上浮過程的仿真研究，基于VC++平臺，開發了仿真軟件，界面如圖2 所示，界面上方采用曲線形式顯示潛艇深度、縱傾、橫傾、沖角、首尾升降舵及方向舵角等操縱運動參數隨時間的變化歷程，界面下方中間部分采用數值實時顯示仿真過程中潛艇運動參數變化情況，界面其余部分為航速、操舵、均衡、高壓氣吹除等控制輸入。

圖2 潛艇高壓氣吹除應急上浮機動仿真分析軟件界面

5 潛艇應急上浮過程運動仿真

5.1 吹除模型的影響

為了研究采用不同吹除模型對潛艇應急上浮橫傾角的影響，采用式（1）～式（6）給出的潛艇大攻角操縱運動數學模型進行仿真計算，同時為了驗證計算結果的準確性，采用與文獻［4］一致的初始條件和挽回控制手段：潛艇均衡好，處于無縱傾定深定常運動狀態，初始指令航速與實際航速uc=u=3 m/s，初始深度ζ=100 m。從0 時刻開始吹除，指令航速同時提高到uc=6 m/s，尾升降舵控制潛艇抬首且縱傾保持為尾傾20°。潛艇首部和尾部4 個主壓載水艙容積及容積中心縱向坐標如表1 所示。

表1 主壓載水艙容積及容積中心縱向坐標

如圖4 所示，實線和虛線分別為采用高壓氣吹除拉瓦爾噴管模型和指數模型計算得到潛艇各狀態參數變化情況，虛線所示結果與文獻［4］基本吻合，從而驗證了本文所采用仿真計算方法的正確性。從仿真結果可以看出，隨著吹除過程的進行以及潛艇的上浮，無論是橫搖角速度p 還是橫傾角φ都在逐漸增大，通過對比可以發現：

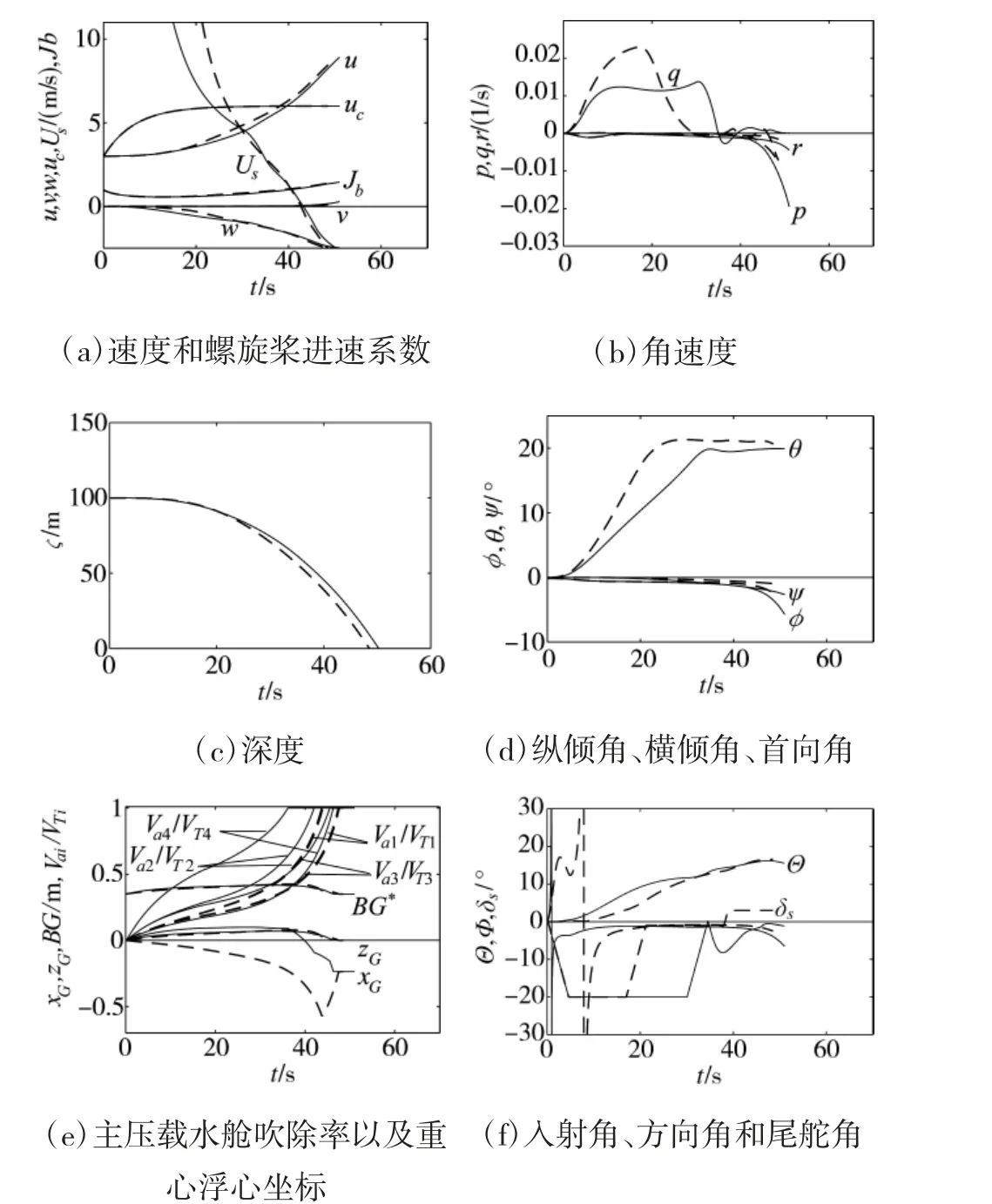
圖4 分別采用高壓氣吹除指數模型和拉瓦爾噴管模型計算得到的潛艇應急上浮時運動參數變化情況

1）指數模型計算的首部的1、2 號主壓載水艙盡管容積差別很大，幾乎同時吹空（1 號略快于2號），尾部的3、4 號主壓載水艙也有類似的結果（3號略快于4 號），這主要是因為該模型假設進入每個主壓載水艙的高壓空氣質量與該水艙的體積成正比，而不考慮水艙排水孔面積、本身容積大小，以及外部背壓對進入該水艙高壓氣流量的影響等因素，影響吹除率的最主要因素為水艙的位置布置。

2）拉瓦爾噴管模型計算得到的吹空順序為：4、2、3、1 號，尾部的4 號主壓載水艙盡管由于艇體尾傾導致排水背壓大，但此壓載水艙容積最小（僅30 m3），所以最先吹空。2、3 號主壓載水艙雖然容積相同，但尾傾使得2 號主壓載水艙排水背壓較小，所以第2排空，3 號主壓載水艙第3 排空。1 號主壓載水艙雖然在上浮過程中排水背壓最小，但體積最大（100 m3），所以1 號主壓載水艙最后排空。因此，綜合考慮水艙的容積、位置布置、艇的運動狀態等因素，拉瓦爾噴管模型的計算結果與實際情況更為符合。

3）在上述拉瓦爾噴管模型計算得到的吹空順序下，潛艇上浮初期，盡管尾升降操上浮滿舵使潛艇抬首，由于4 號主壓載水艙容積最小，排水速度快，很快產生較大的首傾力矩，導致潛艇尾傾形成相對較慢。隨著吹除過程的繼續，首部主壓載水艙的排水量逐漸增大，在上浮過程的中后期，吹除主壓載水艙形成的合力矩逐漸由首傾變為尾傾力矩，最終的合力矩大小為640 t·m，因此，該模型計算得到上浮接近水面時的最大橫傾為6.8°，而指數模型計算結果僅為2.0°。這主要是因為應急上浮過程中尾傾的形成，能將原本與負垂速（-w）方向一致的負浮力轉移了一部分到沿Gx 軸方向來使u 加速，一方面使垂速絕對值增長速度放緩，也即負攻角形成的慢且絕對值將減小，另一方面Gx 軸向速度u 的增加，進一步使攻角減小。因此，尾傾形成快有助于減小應急上浮過程的橫傾角。

5.2 初始深度的影響

為了進一步分析初始深度對潛艇上浮機動的影響，分別設定仿真初始深度為100 m 和150 m，同時吹除全部主壓載水艙，采用拉瓦爾噴管模型計算吹除過程，潛艇狀態參數變化情況如圖5 所示，可以看出，如果初始深度增加到150 m（圖中虛線），上浮時間將會大幅增加，一方面是因為上浮距離增大，另一方面是因為主壓載水艙的吹除率明顯減緩。式（7）中的靜穩性項的變化也減緩，從正值減小到0 的時刻也相較于100 m（圖中實線）吹除的情況推后約20 s，而應急上浮過程中橫傾角迅速增大主要發生在直至上浮到水面的這一階段。因此，從圖5可以看出，分別在100 m 和150 m 吹除全部主壓載水艙，直至上浮到水面狀態，產生的最大橫傾角較為接近。

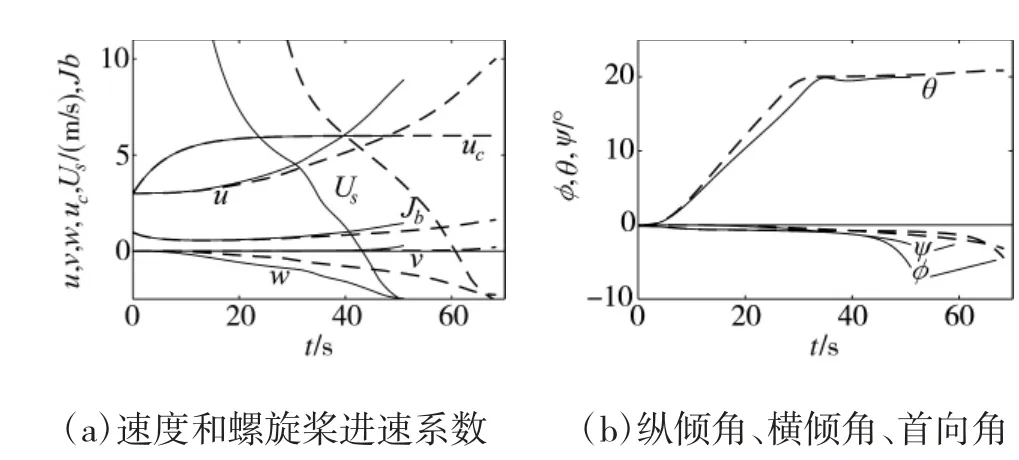
圖5 分別在100 m 和150 m 吹除主壓載水艙時潛艇狀態參數變化情況

5.3 水艙吹除順序的影響

考慮到1 號主壓載水艙位于首部，吹除時有利于尾傾形成進而抑制橫傾增大，而采取同時吹除全部主壓載水艙時，根據4.1 的仿真結果，1 號水艙將會最后吹空，沒有很好地發揮其產生尾傾力矩的效用。為了在上浮過程中較快形成尾傾，可以考慮改變水艙的吹除順序，例如，先吹除1 號主壓載水艙，延時5 s 后吹除剩余的2～4 號主壓載水艙。相應的仿真計算結果如圖6 所示，圖中實線為同時吹除，虛線為先吹除1 號主壓載水艙的情況。可以看出，潛艇尾傾形成時間大大縮短，且上浮過程的最大橫傾角也由6.8°減小到4.1°。結合4.2 可以得出，應急上浮過程的橫傾角主要由所持續的時長決定，并受水艙吹除順序的影響較大，而受初始深度的影響較小。

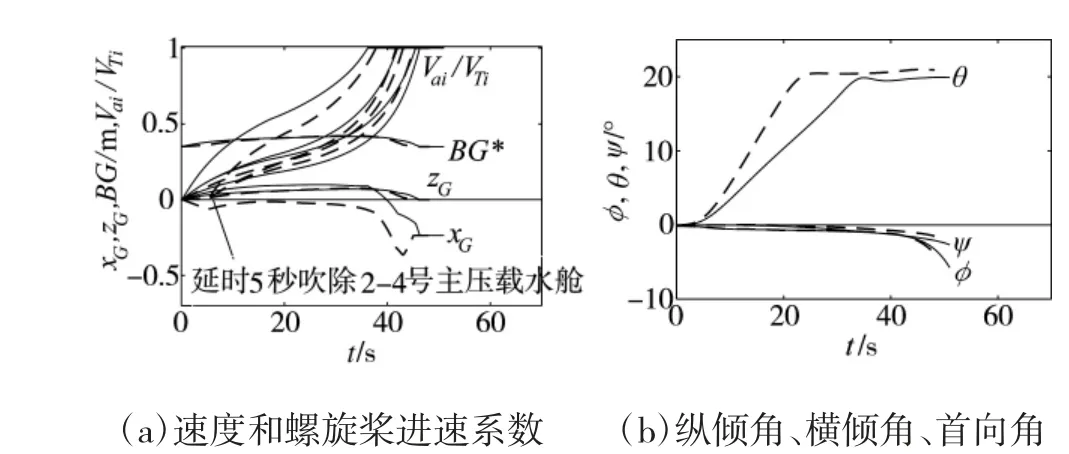
圖6 延時吹除尾部主壓載水艙時潛艇狀態參數變化情況

6 結論

本文以潛艇大攻角水動力試驗結果為基礎，對基于水流入射角和方向角定義下的潛艇大攻角操縱運動數學模型進行了數值仿真求解，采用不同初始狀態以及不同的高壓氣吹除模型，預報了潛艇應急上浮過程的運動狀態，重點分析了上述因素對潛艇應急上浮過程橫傾的影響，仿真結果表明：1）高壓氣吹除拉瓦爾噴管模型，相較于指數模型加入了水艙排水孔面積、潛艇上浮過程水艙外部背壓變化等因素的影響，更能準確計算實艇高壓氣吹除過程，從而提高潛艇應急上浮機動過程運動狀態預報的準確性；2）應急上浮過程中尾傾的形成有助于抑制大的負攻角的形成，從而有助于減小應急上浮過程的橫傾角；3）應急上浮過程中的橫傾角受水艙吹除順序的影響較大，而受初始深度的影響較小。