分組密碼算法Lattice的滑動攻擊*

潘向榮

（中國西南電子技術研究所，四川 成都 610036）

0 引 言

短波通信由于其設備質量輕、機動靈活和抗毀性強等優點，在軍事通信領域占有極其重要的地位。自動鏈路建立（Automatic Link Establishment，ALE）[1]是一種無需用戶操作即可使短波臺站尋找一個合適的頻率并建立鏈路的自動化技術，是短波通信系統中的重要組成部分。自20世紀70年代末至今，自動鏈路建立協議已經發展至第三代，即3G-ALE。與第二代ALE技術相比，3G-ALE技術提高了鏈路建立速度、信道利用率、數據吞吐率，能夠在更低信噪比下實現連接，并支持Internet協議及應用等。全球許多政府和非政府組織均在使用利用ALE技術的無線電通信技術。

SoDark族算法[2]是面向ALE應用的分組密碼算法，實現對ALE標準中協議數據單元（Protocol Data Unit，PDU）中敏感數據的機密性。SoDark族算法包括Lattice算法、SoDark-3算法和SoDark-6算法。Lattice算法應用于第二代ALE（2G ALE），分組長度為24 bit，密鑰長度為56 bit，迭代輪數8輪。3G ALE標準中使用了稱為SoDard-3的版本對26位協議數據單元（PDU）中的24位數據進行加密。SoDark-3的迭代輪數為16輪，其輪函數與Lattice算法相同。由于3G ALE還使用48位的PDU，因此SoDark-3已擴展為具有48位大小的版本，稱為SoDark-6。

Lattice算法是SoDark族算法中的基本算法。對Lattice算法的分析成果將極大地促進對SoDark族算法的成功分析，進而實現對短波通信情報信息的破譯，對獲取其語義內容具有重要意義。本文簡述了Lattice算法、SoDark族算法在短波通信系統中所起的作用及破譯SoDark族算法的意義。第1部分簡要描述Lattice算法；第2部分介紹滑動攻擊的基本原理；第3部分詳細介紹滑動攻擊對Lattice算法的攻擊；第4部分對滑動攻擊算法性能進行分析；第5部分總結全文。

1 Lattice算法介紹

Lattice算法[3]是SoDark族算法中的基本算法，分組長度為24 bit，密鑰長度為56 bit，迭代輪數8輪。Lattice加密算法的輸入包括密鑰（Key）、種子（S eed）和待加密數據3組數據。算法以每24 bit明文數據為單位分別進行加密計算。完整加密過程共包含8次迭代運算，每次迭代運算中的操作數據包括1 Byte密鑰、1 Byte種子和1 Byte源數據。每個步驟運算結果從256×8 bit的加密運算表中查詢相應行列，得到本次計算的8 bit結果。加密算法流程如圖1所示。

加密使用56 bit密鑰和64 bit種子，其中種子由TOD、頻率、Word等構成，結構如圖2所示。64 bit種子包含頻率、當前時間、日期以及wordnumber，其中TOD時間要求是非遞減的。月域由4 bit構成，1代表1月，12代表12月；日期域由5 bit構成，代表從1號～31號；粗時間域采用11 bit，代表從午夜開始的分鐘數，午夜粗時間域和精時間域都清0；精時間域采用6 bit，表示更精確的秒級時間，當時間精度大于分鐘時，精時間域默認為全1（時間質量為6或7）。采用時間同步協議獲取精確時間后，精時間域更新為獲取的精確時間。頻率域每4 bit代表一個十進制數。

Lattice加密算法流程如下。Lattice算法中使用的S盒是一個從域GF(28)到GF(28)的映射，不妨表示為f:GF(28)→GF(28)，如圖3所示。

不妨采用矢量V表示密鑰變量字節，s表示TOD或頻率種子字節。每次加密算法循環從矢量V和s中依次選取1 Byte進行計算，共包括8次循環,完成對24 bit源數據的加密。

假設A為每次加密循環共3個字節中的第1個字節，B為第2個字節，C為第3個字節，A′、B′和C′是本輪運算的輸出，則每一輪中，計算方法如下：

2 滑動攻擊的基本原理

滑動攻擊由David Wagner和Alex Biryukov于1999年提出[4]，適用于算法的迭代過程具有一定的自相似性的密碼算法。在多數情況下，滑動攻擊與迭代輪函數的具體性質和執行輪數無關。，任何可以被分解為執行若干次輪函數F的密碼算法都可以嘗試采用滑動攻擊來分析。換句話說，滑動攻擊的特點是不依賴于密碼算法的輪數，即如果采用滑動攻擊能對某密碼算法進行有效攻擊，則將該密碼算法的迭代輪數增加任意輪后所得到的新算法仍然不能抵抗滑動攻擊。由于SoDark算法的輪函數與Lattice算法的輪函數相同，只是迭代輪數是Lattice算法的2倍，因此采用滑動攻擊對Lattice算法的分析成果能極大地促進對SoDark算法的成功破譯。

用 Fr○Fr-1○Fr-2○…○F1表 示 一 個 輪 數 為 r的迭代分組密碼。滑動攻擊的基本思想[5]是將一個加密過程相對于另一個加密過程“滑動”一輪。如果明密文對(P,C)和(P*,C*)滿足條件F1(P)=P*和Fr*(C)=C*，則稱該密文對為一個滑動對（Slide pair），如圖4所示。滑動對實際上為分析者提供兩組一輪的密碼變換的輸入和輸出。

老師在鼓勵學生閱讀的同時不妨創設情境，讓幾個學生結為一個閱讀小組布置一篇有趣的文章。例如在人教版小學語文二年級上冊的課本中就有《曹沖稱象》、《狐假虎威》等我國有名的短故事，但是很少有涉及到外國寓言童話的小文章，所以老師們不妨給學生布置一些《伊索寓言》、《格林童話》等，每周選擇一個閱讀小組讓小組自行選擇一篇最近閱讀過的小故事進行小組課堂表演，利用表演的方式激發起學生的閱讀興趣。

根據滑動對的定義，滑動攻擊將按以下步驟對密碼算法進行攻擊。假設密碼算法輸入為N個比特，由于輪函數Fi與其使用的輪密鑰相關，若能選擇輪密鑰對(K,K*)使得Fi*=Fi+1，則根據生日攻擊原理，需要2N/2個明文-密文對就能找到滿足上述條件的滑動對。

假定分組密碼算法的分組長度為N，如果采用滑動攻擊能成功破譯該算法，滑動攻擊的復雜度通常接近于O(2N/2)。以色列學者Achiya Bar-On等人[6]針對采用代換-置換網絡（Substitution Permutation Network，SPN）和Feistel結構的密碼算法、GOST及其變體算法，提出了改進的滑動攻擊方法。改進后的滑動攻擊極大地降低了攻擊的時間復雜度。

3 Lattice的滑動攻擊

Lattice算法循環使用7 Byte密鑰V與8 Byte種子s，輪函數Fn+1如下：

若選擇另一個密鑰V*和種子S*，滿足：

則Fi*=Fi+1,1≤i≤7，恰好滿足對其實施滑動攻擊的條件。基于上述討論，本文分析采用滑動攻擊能有效破譯Lattice算法的可行性。下面對Lattice算法實施滑動攻擊的過程如圖5所示。

注意到輪函數F1：

使用密鑰V[0]、V[1]、V[2]，輪函數F9為：

使用密鑰 V[3]、V[4]、V[5]，若兩組明文 - 密文 對 (P,C)和 (P*,C*)滿 足 F1(P)=P*， 由 于 Fi*=Fi+1，1≤i≤7，則一定有F8*(C)=C*，也就是已知輪函數F1、F9的輸入與輸出。在已知種子s的前提下，可以計算出 V[0]、V[1]、V[2]、V[3]、V[4]、V[5]，具體計算表達式如下：

計算出的6 Byte密鑰不一定是正確的密鑰，窮舉V[6]，可得到完整的7 Byte密鑰。通過兩個明文-密文對，可驗證分析得到的密鑰是否正確。不妨假設N是明文-密文對的個數，攻擊算法的偽代碼如下：

攻擊算法成功的關鍵在于存在兩組明文-密文對(P,C)和(P*,C*)滿足F1(P)=P*。在明文隨機選取的前提下，它的概率Pr為：

4 對Lattice算法的滑動攻擊算法性能分析

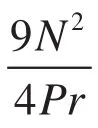
本文通過計算機仿真實現了對Lattice算法的滑動攻擊實例。本文設置Lattice算法的56 bit密鑰為C2 28 4A 1C E7 BE 2F，種子為543bd88000017550。通過使用上述滑動攻擊方法和對應的攻擊算法，分析得到Lattice密碼算法的密鑰與預置的密鑰完全一致，如圖6所示，表明本文成功地利用了滑動攻擊方法對Lattice密碼算法實施了完全破譯。

5 結 語

SoDark族分組密碼算法用于實現第二代和第三代自動鏈路建立（Automatic Link Establishment，ALE）系統所發送消息的機密性。Lattice算法是SoDark家族算法中的基本算法。本文基于滑動攻擊原理，設計了采用滑動攻擊分析Lattice算法的攻擊算法，并通過計算機仿真給出了對Lattice算法采用滑動攻擊進行密鑰恢復的實例。仿真結果表明，本文采用滑動攻擊方法對Lattice算法實施攻擊的正確性和有效性。本文的分析成果對分析具有更高輪數的SoDark-3和SoDark-6密碼算法提供了堅實基礎。在后續的研究工作中，將進一步采用滑動攻擊方法開展對SoDark-3和SoDark-6兩個密碼算法的分析。