基于大數據和Louvain算法的企業風險擔保圈構建

羅桑強巴

(四川大學計算機學院，成都 610065)

0 引言

擔保圈是企業之間互相擔保、交叉擔保和連環擔保形成的特殊利益集體[1]。擔保圈內的各家企業成了息息相關的命運共同體，只要其中一家企業陷入債務危機，其他企業將或多或少受到牽連，嚴重時可能對整個區域經濟產生巨大影響[2]。因此企業擔保圈的風險管理不僅影響企業融資，更影響著區域金融穩定。2003年的新疆“啤酒花”擔保圈事件、2004年的重慶“覃輝”擔保圈事件、2006年河北寶碩股份擔保圈事件均給當地金融生態帶來了一定程度的破壞，擔保圈的“多米諾骨牌效應”會將風險沿著擔保鏈傳遞和擴散到圈內的各個企業，各企業的風險可能會被化解，也有可能放大、轉遞和擴散，導致區域金融生態發生變化，甚至可能會發生系統性金融風險。

企業擔保圈風險監管是非常有必要和迫在眉睫的事情，但是目前現有經濟環境下，擔保是解決中小微企業融資問題的一條主要途徑，怎樣將監管力度和解決中小微企業融資難、融資貴的問題找到一個平衡點是需要研究的問題。劉悅芹等人(2015)在研究擔保圈風險中指出，目前國內擔保圈研究較為薄弱，主要存在擔保圈概貌不清，風險不明、阻斷不力等問題，并提出了基于有向遍歷算法的擔保圈繪制辦法[3]。劉錚(2019)提出了基于寬度優先搜索的擔保圈識別辦法[4]。Tan Bo(2017)提出基于知識圖譜算法的客戶關聯關系構建方法[5]。上述擔保圈的構建方法主要以監管單位或銀行收集的擔保信息數據為主，對企業的內在關系和隱性擔保關聯等未考慮完全，并以寬度優先和遍歷算法等繪制的擔保圈可能出現超級擔保圈，即包含上百家企業的超級擔保圈，且不能再對超級擔保圈進行有效的分割，風險傳導不一定會擴散至整個擔保圈，且無法精確預警需要防范風險的企業，可能發生整個擔保圈的恐慌，導致其他的金融風險出現。

1 擔保關系矩陣構建

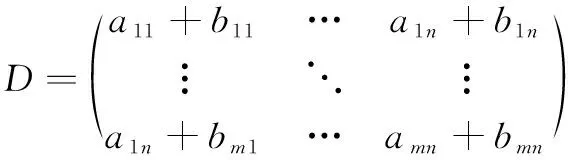
2 基于Louvain算法的風險擔保圈繪制

風險擔保圈的繪制方便了擔保圈的風險識別和企業風險傳遞的研究。本文主要通過Louvain算法對上節構建的擔保關系矩陣進行聚類，并結合擔保圈內企業的特性進行分析。基于該算法的聚類，可以從多個層次進行擔保圈的繪制，并有效引入了企業關聯關系和相同法人信息，從而更準確地刻畫企業風險擔保圈，也為下一步從時間維度進行擔保圈分析提供了思路。

Louvain 算法是Vincent D.Blondel等人在2008年提出的[5]，是常用聚類算法的一種，也是目前社區聚類算法中計算速度最快的算法，目前論文引用已達1萬多次。該算法一種基于模塊化優化的啟發式方法，通過計算模塊增量值ΔQ(delta modularity)確定節點是否加入新的社區。主要包含兩個重要的指標模塊度值Q，和模塊度增量值ΔQ，通過Q值可以確定社群的分類度，其取值范圍為[0，1]，值越大分類度越好。Louvain算法的具體公式如下：

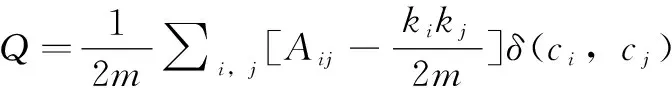
Louvain算法構建多層次企業風險擔保圈主要以迭代次數確定，具體過程如下：

輸入：擔保關系矩陣Dmn

第一步：假設每個企業單位可作為一個擔保圈，遍歷所有企業，將鄰近企業加入到擔保圈，計算ΔQ是否增加，直到所有擔保圈均無法吸收新的節點，此時得到第一層次的風險擔保圈；

第二步：將第一步劃分的擔保圈作為一個節點，分別計算節點之間的權重，重復第一步，此時得到第二層次的風險擔保圈；

第三步：在進行多輪迭代后Q值不在變化或者達到約定迭代次數，得到對應層次的風險擔保圈。

3 風險擔保圈繪制結果及分析

通過對樣本數據處理結果，風險擔保圈指標如表1。

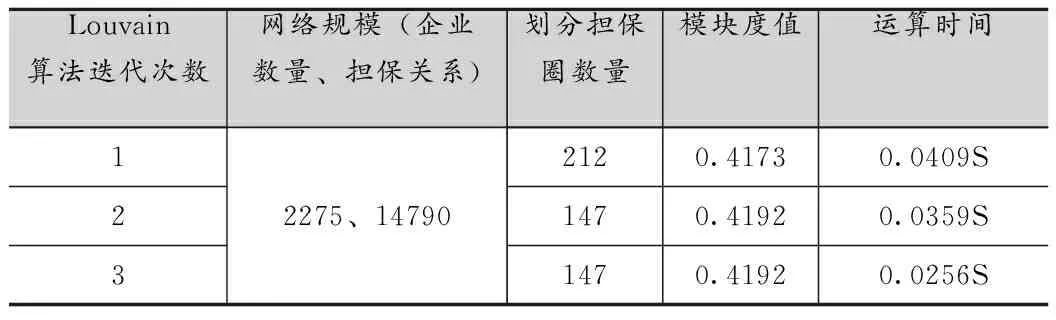
表1

4 結語

本文引入在構建擔保關系矩陣時同一法人的企業和企業隸屬關系，并提出基于Louvain算法的企業風險擔保圈劃分方法。該方法層次劃分經過質性分析能更真實地反映擔保圈，為下一步擔保圈風險分析和阻斷提供了基礎，具有一定的實際意義。