改進(jìn)的函數(shù)連接型非線性回聲對消算法
王仁杰,楊曉敏,蘆璐
(四川大學(xué)電子信息學(xué)院,成都 610065)
0 引言
近年來,通信和網(wǎng)絡(luò)技術(shù)不斷發(fā)展,使得人們對通信的質(zhì)量提出了新的要求,其中最主要的就是語音通話質(zhì)量。聲學(xué)回聲是降低語音通話質(zhì)量的重要因素之一[1]。回聲是由于麥克風(fēng)和揚聲器之間的回聲路徑的脈沖響應(yīng)耦合效應(yīng)而產(chǎn)生的。由于人耳對回聲非常敏感,延遲超過10ms的回聲就能被人耳捕捉到,超過32ms的回聲就會嚴(yán)重干擾通話質(zhì)量。因此,如何消除聲學(xué)回聲具有重要的現(xiàn)實意義。目前最普遍應(yīng)用的方法是基于自適應(yīng)濾波的回聲消除器(Acoustic Echo Cancellation,AEC)。AEC的基本原理是運用自適應(yīng)濾波算法對回聲路徑的脈沖響應(yīng)進(jìn)行估計,其本質(zhì)是一個系統(tǒng)辨識的問題。然而當(dāng)回聲路徑存在非線性的特性時,傳統(tǒng)的自適應(yīng)濾波算法,比如最小均方算法(Least Mean Square,LMS)、歸一化最小均方算法(Normalized Least Mean Square,NLMS)的性能會出現(xiàn)明顯的下降。因此,如何對回聲路徑中的非線性特性建模,提出有效的非線性回聲對消方法具有重要意義[4]。
目前的非線性回聲對消的方法中,具有代表性的有以下兩種。文獻(xiàn)[1]中提出了一中基于函數(shù)連接的非線性自適應(yīng)濾波算法用于回聲對消(Split Functional Link Adaptive Filter,SFLAF)。該方法的特點是對輸入信號進(jìn)行非線性擴(kuò)展,具體地說,是通過三角函數(shù)函數(shù)連接擴(kuò)展,將未經(jīng)過變換的信號和經(jīng)過變換的信號分別用兩個濾波器進(jìn)行濾波,以此達(dá)到同時對回聲路徑的線性和非線性特性建模的目的。文獻(xiàn)[2]將回聲路徑中的非線性變換設(shè)定為一種sigmoid變換,在進(jìn)行濾波之前對sigmoid的參數(shù)進(jìn)行估計,并結(jié)合RLS的快速收斂和強(qiáng)跟蹤能力,能快速使得估計值收斂到真實值。
受以上方法的啟發(fā),本文結(jié)合以上兩種方法,對函數(shù)連接型自適應(yīng)回聲對消器做出改進(jìn):其中在文獻(xiàn)[1]中的SFLAF的線性濾波器中引入文獻(xiàn)[2]的RLS-sigmoid算法,將回聲路徑中的非線性變換設(shè)定為sigmoid類型的變換。對非線性變換的參數(shù)進(jìn)行估計,進(jìn)一步增強(qiáng)了算法的非線性建模能力,提升了回聲對消的效果。
1 SFLAF算法
1.1 函數(shù)連接型自適應(yīng)濾波器FLAF
圖1給出了一個函數(shù)連接型濾波器FLAF的結(jié)構(gòu)。FLAF包括兩個階段:輸入信號的非線性擴(kuò)展以及后續(xù)的線性自適應(yīng)濾波。假設(shè)在n時刻,F(xiàn)LAF接收到的輸入信號向量為x(n)=[x(n),x(n-1),…,x(n-L+1)],其中L表示輸入向量的長度。FLAF利用函數(shù)擴(kuò)展塊(Functional Expansion Block,F(xiàn)EB)對其進(jìn)行處理。FEB由一系列的函數(shù)組成,它們可以是正交基函數(shù)的完備集,滿足Stone-Weierstrass近似定理[5]。FEB將輸入信號進(jìn)行擴(kuò)展,映射到更高的維度,從而可以提高對系統(tǒng)的非線性建模能力。而所謂的函數(shù)連接(Functional Link),本質(zhì)上是就是FEB這個函數(shù)集合中的函數(shù)算子[6]。
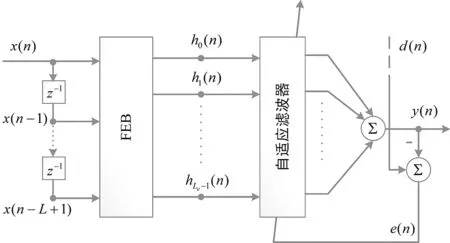
圖1 FLAF結(jié)構(gòu)示意圖


(1)
其中,0≤i≤L-1,L是輸入向量原有的長度。
而對于長度為L的輸入向量,經(jīng)過FEB處理后,最終得到擴(kuò)展向量hn。

=h0(n),h(n),…,hLe-1(n)〗T
(2)
其中,Le代表擴(kuò)展后向量的長度,易得,Le=LQ。
FEB中函數(shù)集合的選擇對FLAF的性能有重要的影響,需要根據(jù)具體的應(yīng)用場景和處理的信號而定。這些滿足Stone-Weierstrass近似定理的基函數(shù),可以是正交多項式的子集,例如切比雪夫[7]、勒讓德[10]和三角函數(shù)多項式[11];也可以是近似函數(shù),例如sigmoid函數(shù)和高斯函數(shù)。這其中,三角函數(shù)多項式由于在均方意義上能最好的表征任何的非線性函數(shù),并且相較于冪級數(shù)多項式計算復(fù)雜度也較低,因此也被運用的最為廣泛[8]。
考慮輸入向量x(n)中的第i個元素,0≤i≤L-1,一般的三角函數(shù)FEB可以表示為:

(3)
其中1≤p≤P,P是三角函數(shù)連接擴(kuò)展的階數(shù)。而0≤j≤Q,在這種情況下,F(xiàn)EB中函數(shù)的個數(shù)Q=2P+1。1代表線性的元素,即沒有通過三角函數(shù)變換,和輸入向量中元素完全一樣的元素。因此,這種情況下得到的擴(kuò)展向量同時包含了線性和非線性的元素。
最后,只需要對擴(kuò)展向量進(jìn)行簡單的線性濾波就可以完成整個FLAF過程。濾波器的目標(biāo)就是在越小的誤差范圍內(nèi)準(zhǔn)確的對非線性建模。線性濾波器的權(quán)值向量記作w(n)=[w0(n),w1(n),…,wLe-1(n)]T,期望信號記作d(n),則FLAF的誤差信號表示為:
e(n)=d(n)-y(n)
=d(n)-hT(n)w(n)
(4)
可以看出,e(n)的最小化取決于對權(quán)值向量w(n)的估計。我們可以采用任意一種基于梯度下降法的自適應(yīng)算法來更新權(quán)值向量[9]。
1.2 分裂函數(shù)連接型自適應(yīng)濾波器SFLAF
分裂型FLAF(Split Functional Link Adaptive Filter,SFLAF)的結(jié)構(gòu)如圖2所示。所謂分裂,就是將經(jīng)過FEB擴(kuò)展后的信號中的線性元素和非線性元素解耦合,分別通過兩個并行的自適應(yīng)濾波器,用總體誤差分別對兩個濾波器的權(quán)值向量進(jìn)行更新。這其中,線性濾波器接收未經(jīng)過函數(shù)變換的輸入向量,旨在估計回聲路徑;而非線性濾波器接收經(jīng)過三角函數(shù)變換的向量,旨在對回聲路徑中的非線性變換建模[1]。
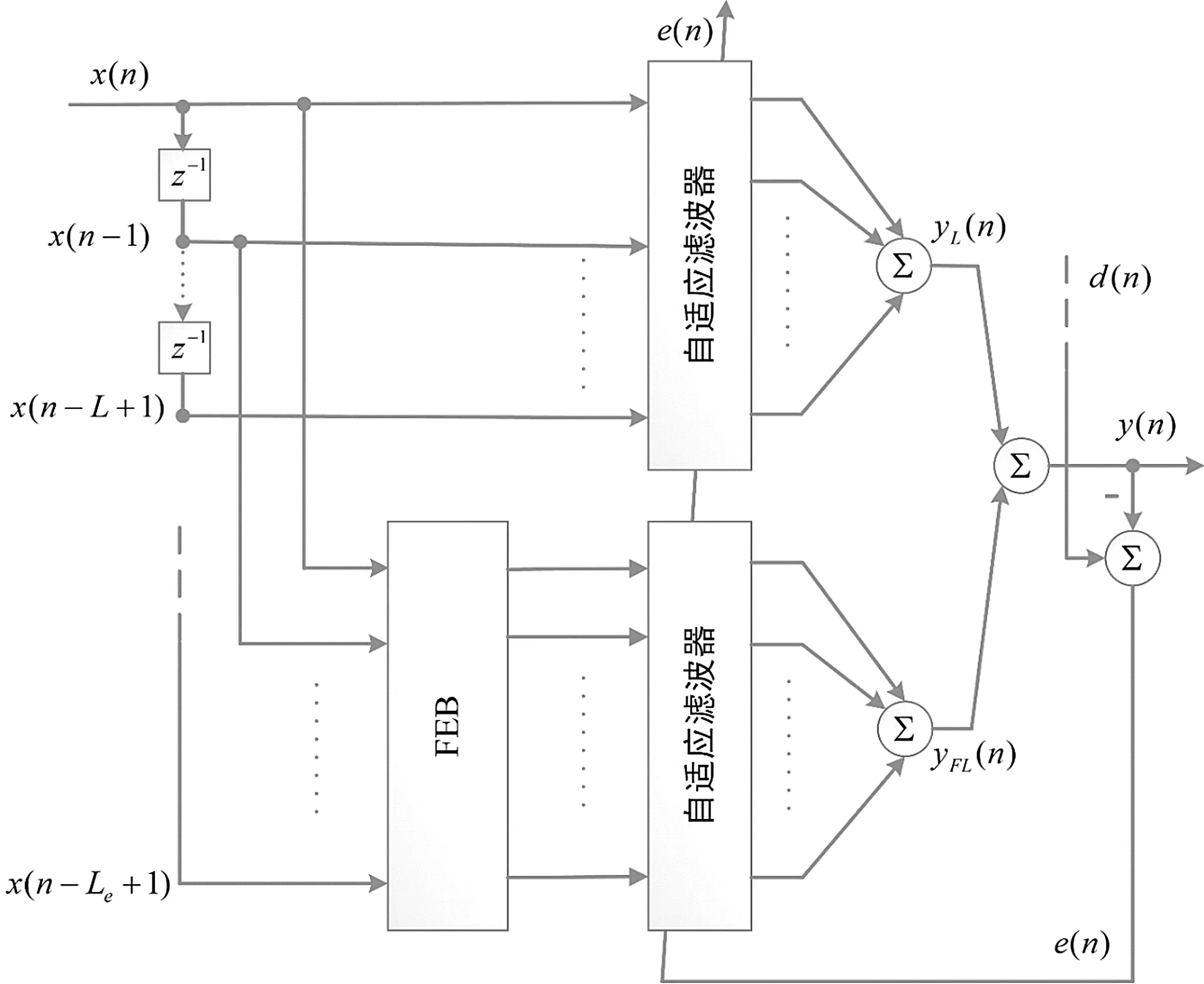
圖2 SFLAF結(jié)構(gòu)示意圖
SFLAF的輸出信號由線性濾波器和非線性濾波器的輸出信號疊加而成:
y(n)=yL(n)+yFL(n)
(5)
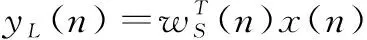
2 SFLRLS-sigmoid算法
文獻(xiàn)[2]提出了一種對回聲路徑中的非線性特性進(jìn)行建模的有效方法:其將非線性畸變建模為sigmoid函數(shù),并通過對其參數(shù)的估計來擬合非線性。其結(jié)構(gòu)如圖3所示。該算法分別用最小均方算法LMS和遞歸最小二乘算法RLS(Recursive Least Square,RLS)來更新sigmoid變換的參數(shù)和濾波器的權(quán)值向量。得益于RLS算法快速的收斂速度和跟蹤能力,能快速使得估計值收斂到真實值。

圖3 RLS-sigmoid結(jié)構(gòu)示意圖
受此啟發(fā),我們將RLS-sigmoid算法引入到SFLAF的線性分支中,新的算法記作Split Functional Link RLS-sigmoid,SFLRLS-sigmoid。算法結(jié)構(gòu)如圖4所示。

圖4 提出的SFLRLS-sigmoid算法結(jié)構(gòu)示意圖
首先對長度為L的輸入信號x(n)分別進(jìn)行sigmoid變換和函數(shù)擴(kuò)展。輸入信號x(n)通過(6)中的sigmoid變換:
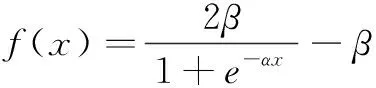
(6)
其中,α和β是sigmoid變換的兩個參數(shù)。得到xS(n)=[f(x(n)),f(x(n-1)),…,f(x(n-L+1))]。同時,輸入信號x(n)通過三角函數(shù)連接進(jìn)行函數(shù)連接擴(kuò)展,得到擴(kuò)展后的輸入信號xFL(n)=[φ1(x(n)),φ2(x(n)),…,φ2P(x(n))]。
接著,分別將xS(n)和xFL(n)通過自適應(yīng)濾波器:yS(n)=wST(n)xS(n),yFL(n)=wFLT(n)xFL(n);其中,wS(n)和wFL(n)為對應(yīng)濾波器的權(quán)值。然后得到總體的濾波輸出:y(n)=yS(n)+yFL(n)。將近端麥克風(fēng)拾取到帶回聲的近端信號d(n)與總體濾波輸出y(n)相減后再回送給遠(yuǎn)端,回送信號為總殘差信號e(n)=d(n)-y(n)。
利用殘差信號e(n)對下一次迭代的sigmoid變換的參數(shù)按照如下方法進(jìn)行更新:

(7)
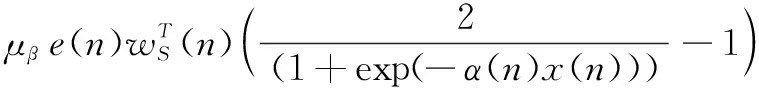
(8)
其中,α(n)和β(n)是在n時刻對α和β的估計值,μα和μβ是兩個步長參數(shù)[2]。wS(n)利用遞歸最小二乘算法(RLS)更新:
P(0)=δ[-1]I
(9)

(10)
wS(n+1)=wS(n)+k(n)e(n)
(11)
P(n+1)=λ-1P(n)-λ-1k(n)xT(n)P(n)
(12)
其中,矩陣P(n)是逆相關(guān)矩陣,I是單位矩陣,k(n)是增益向量,λ和δ分別是遺忘因子和正則化參數(shù)[9]。wFL(n)利用歸一化最小均方算法(NLMS)更新:
(13)
其中,μFL和σ分別是步長和正則化參數(shù),‖·‖為二范數(shù)運算。
3 實驗與分析


圖5 回聲路徑的脈沖響應(yīng)
按照以上實驗條件,用本文方法與現(xiàn)有的兩種方法進(jìn)行回聲消除實驗,各種算法的參數(shù)具體取值如表1所示。圖6給出了本文方法和文獻(xiàn)[2]對sigmoid非線性變換的參數(shù)α和β的估計值的迭代曲線。可以看出,兩種方法都能收斂到真實的參數(shù)值,而SFLRLS-sigmoid的收斂速度更快。

表1 實驗各算法的最優(yōu)參數(shù)近似取值

圖6 sigmoid參數(shù)α和β學(xué)習(xí)曲線
選擇回聲返回?fù)p失增強(qiáng)(Echo Return Loss Enhancement,ERLE)作為性能指標(biāo):
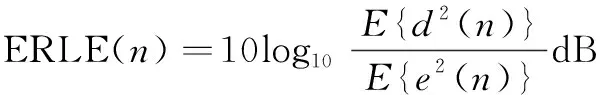
其中,E{·}表示求期望運算。圖7給出了3種方法的ERLE對比曲線。可以看出,由于RLS-sigmoid能準(zhǔn)確估計sigmoid非線性變換的參數(shù)值,其效果要優(yōu)于SFLAF。而本文方法在RLS-sigmoid的基礎(chǔ)上與SFLAF結(jié)合,進(jìn)一步加快了sigmoid非線性變換參數(shù)值的收斂過程。因此,相較于文獻(xiàn)[1]、[2]的方法,本文方法的收斂速度更快,并且收斂穩(wěn)定后的ERLE值也更大。
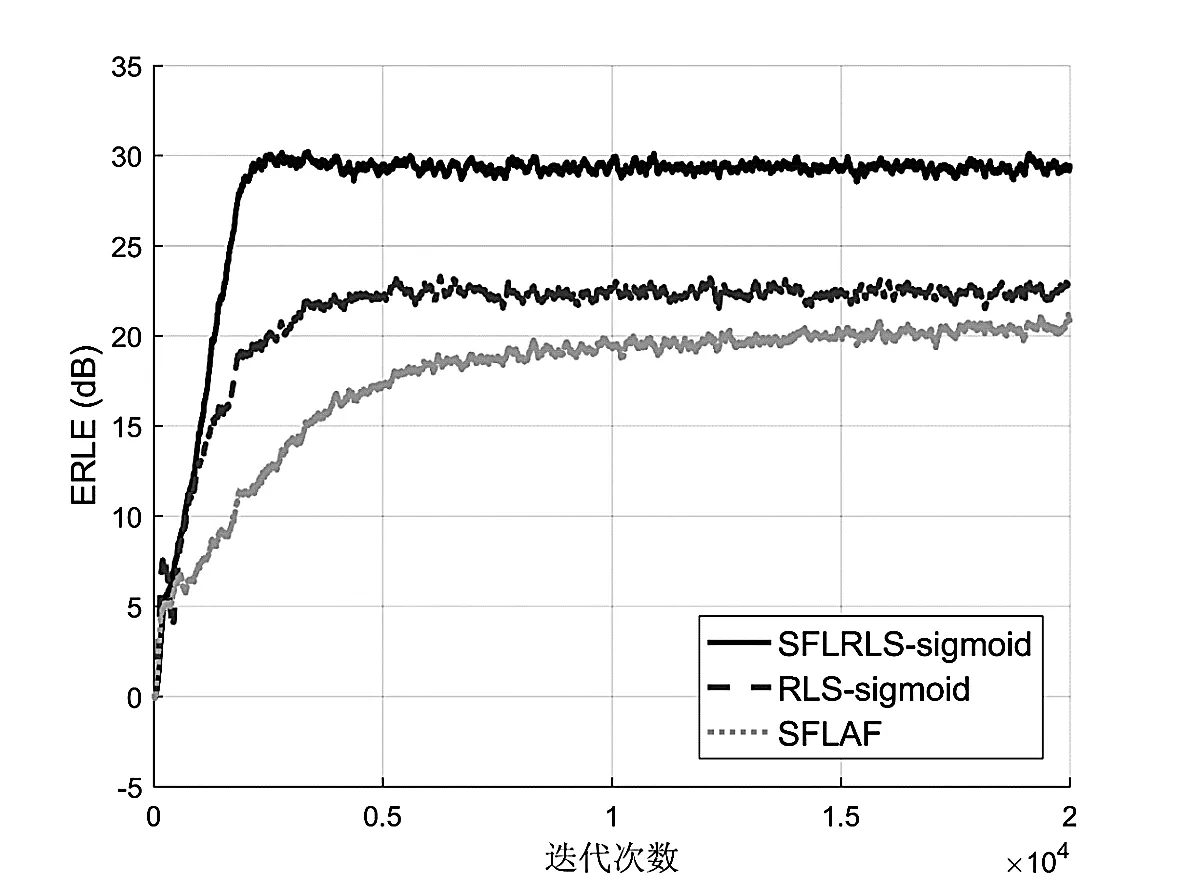
圖7 回聲對消的ERLE對比曲線
4 結(jié)語
本文提出了一種改進(jìn)的基于函數(shù)連接的非線性回聲對消方法SFLRLS-sigmoid,通過實驗證明,這兩種方法的結(jié)合與它們各自單獨作用相比較,進(jìn)一步提升了對回聲路徑的非線性特性的建模能力,收斂速度更快,回聲對消的效果更好。

