多因素觀測來源不確定的多目標跟蹤算法*

王 穎

（商丘職業技術學院機電系，河南 商丘 476000）

0 引言

傳統多目標濾波器在跟蹤前需要建立目標與觀量的關聯［1-3］，因此，該類濾波器難以應用于目標數目時變的目標跟蹤場景，且計算復雜度隨虛警增多呈指數增長。基于有限集統計學［4］的概率假設密度（PHD）［5］濾波器繞過了復雜的數據關聯，因此，受到了目標跟蹤領域越來越多學者的關注［6-9］。線性高斯噪聲動態系統下，高斯混合PHD（GMPHD）給出了PHD 濾波器的一種閉合解［10］。

GMPHD 濾波器具有目標狀態提取簡便和計算復雜度低等優點，被廣泛應用于目標跟蹤領域［11-13］。針對雜波環境下雜波和目標觀測來源不確定的目標檢測和跟蹤問題，Baisa 等［14］提出一種基于GMPHD 的多目標多類型濾波（MTMTF）算法。該算法采用目標分類更新策略，克服了GMPHD 濾波器更新步中不同類型目標觀測的相互干擾。然而，MTMTF算法只能處理雜波與目標觀測的歸屬不確定性問題，無法解決近鄰目標觀測來源不確定的問題。標準Bayes 濾波框架下，Aoki 等［15］從理論上分析了雜波環境下，源于近鄰目標的觀測不確定性和觀測-目標間關聯等問題。然而，文獻［15］僅僅從理論上給出了近鄰目標觀測不確定性的分析與證明，沒有給出具體的實現。針對由不精確檢測導致的觀測來源不確定問題，Yazdian-Dehkordi 等［16］提出一種多掃描懲罰GMPHD（NSP-GMPHD）濾波器。借助于目標前N 個時刻的狀態估計，NSP-GMPHD 濾波器從當前時刻后驗強度中估計不同目標的狀態。密集雜波跟蹤場中，多掃描推測技術的引入使得NSP-GMPHD 濾波器的計算效率很低。基于權重指數衰減函數和多幀技術，Zhang 等［17］提出一種狀態精度和計算效率均衡的GM-PHD（IUMF-GMPHD）濾波器。通過利用前一時刻目標的權值，權重指數衰減函數，可以有效地解決由近鄰目標觀測不確定性導致的目標權值失衡問題，以及雜波與目標量測觀測來源不確定問題。然而，多幀技術的引入同樣使得IUMF-GMPHD 濾波器的計算代價較高。此外，含有多類型觀測來源不確定的密集雜波多目標跟蹤環境下，IUMF-GMPHD 濾波器的狀態估計精度仍相對較低。

通過改進GMPHD 濾波器，提出一種多因素觀測來源不確定的多目標跟蹤算法。通過引入標記和權重向量作為目標的輔助參量，結合高斯分量合并策略、目標狀態估計策略和高斯分量優化策略，本文算法能夠提高多因素觀測來源不確定跟蹤環境下目標狀態估計精度和濾波迭代效率。

1 基于隨機有限集的GMPHD 濾波器

預測步：假設k-1 時刻后驗強度由高斯混合表示為

其中，ps，k為存活概率，第i 個高斯分量的預測均值和預測協方差分別為

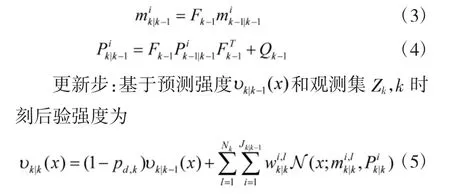
其中，等式右側第1 項為漏檢項后驗強度，第2 項為觀測更新項后驗強度。

2 觀測來源不確定的GMPHD 算法

目標觀測來源不確定主要由3 種因素所導致。1）雜波因素。未知目標-觀測關聯條件下，濾波器通常難以有效地區分雜波和源于目標的觀測。2）低檢測概率因素。低檢測概率的目標跟蹤環境下，源于目標的觀測可能難以被傳感器探測到。3）多目標相互近鄰因素。當目標相互近鄰時，濾波器難以區分源于不同目標的觀測，將導致目標狀態更新錯誤和目標分量錯誤合并。

2.1 高斯分量合并策略

2.2 目標狀態估計策略

當傳感器的檢測概率較低時，場景中所有真實目標難以被傳感器全部探測。采用不完整觀測集更新預測強度后所得到的后驗強度的精度相對更低，因此，部分目標狀態難以從低精度后驗強度中估計。為了從低精度后驗強度中正確地估計目標狀態，提出一種新的目標狀態估計策略。

2.3 高斯分量優化策略

3 實驗結果與分析

采用本文算法分別對NSP-GMPHD［16］和IUMFGMPHD［17］濾波器進行改進，得到Novel-NSPGMPHD 和Novel-IUMF-GMPHD 濾波器。基于OSPA 距離［18］和運算時間，將改進后的濾波器與原始濾波器進行性能對比，其中，OSPA 距離的兩個參數分別為p=1 和c=200。實驗結果為200 次Monte-Carlo 仿真實驗的平均值。目標存活概率ps，k=0.99，分量數目截取閾值=4，存活比率閾值μs=0.4，新生比率閾值μn=0.6，元素數目閾值ρTH=5，狀態抽取閾值=0.5。狀態噪聲服從零均值、標準差為0.5的高斯分布，觀測噪聲服從零均值、標準差為49 的高斯分布。

實驗1：雜波和近鄰目標因素引起的觀測來源不確定

實驗場景為一個［-700 m，700 m］×［-700 m，700 m］二維監視區域，其中該區域中含有3 個相互交叉的目標。圖1 給出了實驗場景的100 s 仿真示意，其中雜波數目服從均值為10 的均勻分布和檢測概率pd，k=0.95。

圖1 目標軌跡和觀測

圖2 給出了100 次Monte-Carlo 實驗的OSPA距離和運算時間的結果對比。Novel-NSP-GMPHD和Novel-IUMF-GMPHD 濾波器具有較小的OSPA距離的原因為：高斯分量合并策略的應用，極大地避免了基于近鄰目標觀測相互干擾的觀測來源不確定所導致的高斯分量合并錯誤；目標狀態估計策略的引入，較好地改善了由低檢測概率引起的觀測來源不確定所導致的目標狀態漏估計。由于高斯分量優化策略能夠有效地降低濾波迭代中后驗強度內無效分量的比重，因此，Novel-NSP-GMPHD和Novel-IUMF-GMPHD 濾波器的迭代效率均高于NSP-GMPHD 和IUMF-GMPHD 濾波器的迭代效率。良好的濾波性能表明，本文算法能夠有效地解決多因素觀測來源不確定下的多目標跟蹤問題。

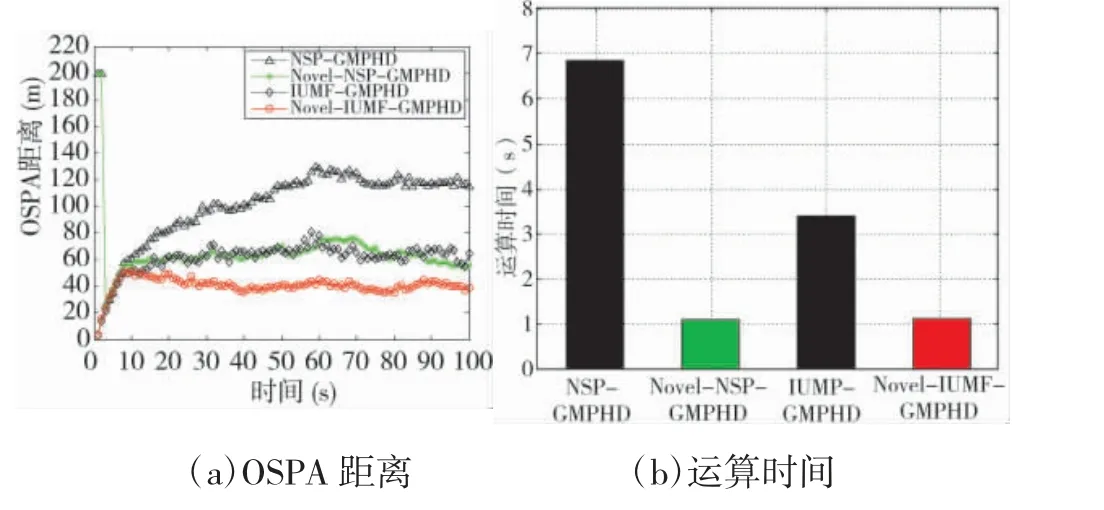
圖2 各濾波器100 次Monte-Carlo 結果對比

實驗2：不同檢測概率環境下的多因素觀測來源不確定

圖3 為檢測概率對各濾波器性能影響的結果對比，其中雜波數目服從均值為8 的均勻分布且其他場景參數與實驗1 相同。相較于NSP-GMPHD 和IUMF-GMPHD 濾 波 器，Novel-NSP-GMPHD 和Novel-IUMF-GMPHD 濾波器，在各個檢測概率處均具有較小的OSPA 距離和較少的運算時間。得益于高斯分量優化策略能較好地控制分量數目，兩個改進濾波器的運算時間幾乎不隨檢測概率的變化而變化。該組實驗結果表明：在高斯分量合并和優化策略的協助下，目標狀態估計策略，能夠改善由低檢測概率引起的觀測來源不確定所導致的目標漏估計及計算效率問題。

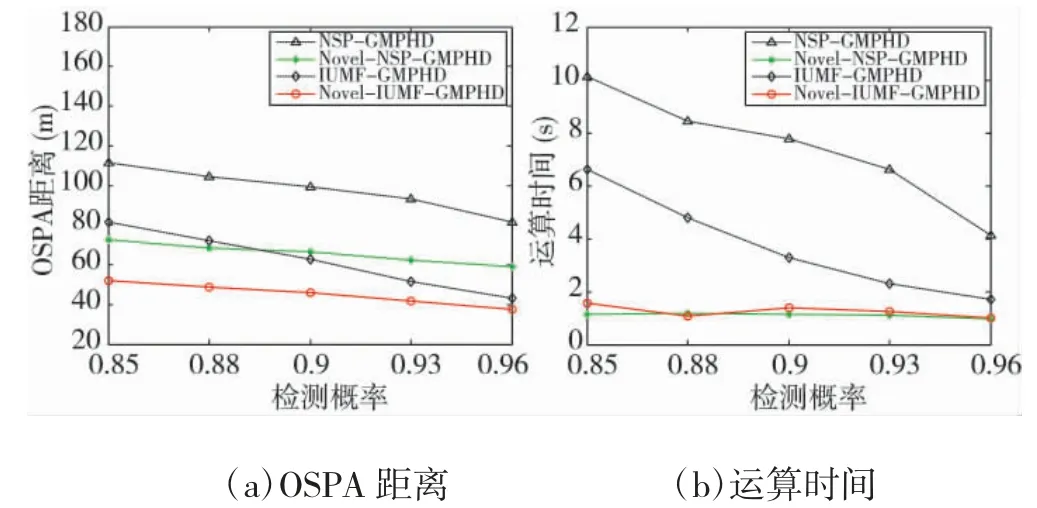
圖3 檢測概率對各濾波器性能影響對比

實驗3：不同雜波數目環境下的多因素觀測來源不確定

圖4 給出了各濾波器在不同雜波均值場景下的結果對比，其中檢測概率pd，k=0.93 且其他場景參數與實驗1 相同。 相較于NSP-GMPHD 和IUMF-GMPHD 濾 波 器，Novel-NSP-GMPHD 和Novel-IUMF-GMPHD 濾波器總體上具有較小的OSPA 距離和較少的運算時間。該組實驗結果表明：基于目標狀態估計策略和高斯分量優化策略的輔助，高斯分量合并策略，能夠提高由雜波和近鄰目標所導致的觀測來源不確定下的目標狀態估計精度和計算效率。

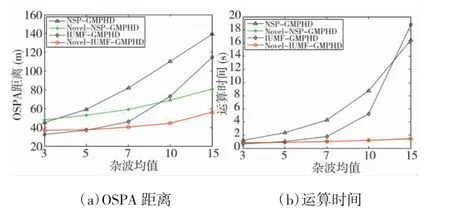
圖4 雜波數目對各濾波器性能影響對比

實驗4：分量數目截取閾值對濾波算法性能的影響

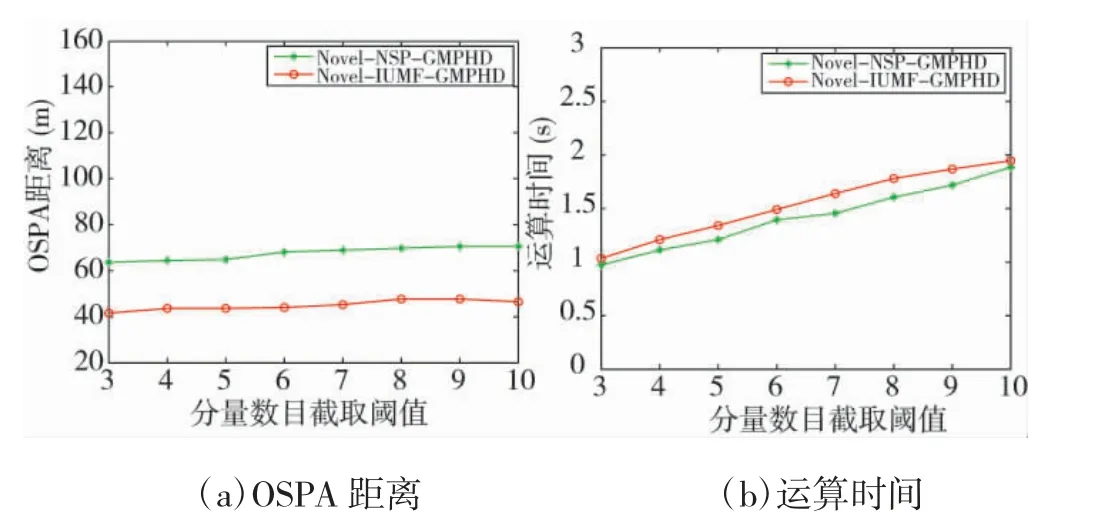
圖5 分量數目截取閾值對本文算法的影響

4 結論

本文提出一種針對多因素觀測來源不確定的多目標GMPHD 濾波器。通過迭代地傳遞目標標記、目標權重向量和目標后驗強度，高斯分量合并策略，能夠有效地避免由雜波和近鄰目標引起的觀測來源不確定所導致的高斯分量合并錯誤，目標狀態估計策略，改善了由低檢測概率引起的觀測來源不確定所導致的目標漏估計，高斯分量優化策略通過減少后驗強度中無效的高斯分量，以降低濾波器的計算代價。實驗結果表明，本文算法能夠有效地改善多因素觀測來源不確定環境下的目標狀態估計精度和濾波迭代效率。