模糊云資源調度問題的RIOPSO 算法

李成嚴，宋 月，馬金濤

哈爾濱理工大學 計算機科學與技術學院，哈爾濱 150080

云資源調度是云計算中的核心內容，文獻[1]為了使完工時間最短，建立了相應的云計算調度模型。文獻[2]在調度過程中，保證服務質量的前提下，使云服務提供商獲取最大的利益。文獻[3]為了使能源消耗最小，建立了實時調度系統。以上這些研究中，使用的都是確定的執行時間。但是由于任務執行的不可預見性，在任務執行完成之前，執行時間只能是一個估計的值，這就導致任務的執行時間具有不確定性，因此本文在建立云資源調度模型時，對任務執行時間具有不確定性的情況進行了考慮。在解決實際問題時，數學模型可以分為三類，分別為確定性的數學模型、隨機性的數學模型和模糊性的數學模型，對于不確定的需要估計的問題，就需要模糊數學模型進行解決。文獻[4]使用模糊遺傳系統對疾病的診斷時間進行了時間復雜度的分析，文獻[5]研究了云環境下基于模糊神經網絡算法的作業調度。在本文中，使用三角模糊數對不確定的任務執行時間進行表示[6]，建立了模糊的云資源調度模型。

云資源調度問題是一個NP 完全問題[7]，沒有有效的多項式算法。為解決云資源調度問題，國內外學者常常采用智能優化算法來實現上述目標。智能優化算法包括遺傳算法（genetic algorithm，GA）[8]，粒子群算法（particle swarm optimization，PSO）[9]和蟻群算法（ant colony optimization，ACO）[10]等。相比于GA 算法，PSO 算法在處理和實現上不存在重疊和突變現象，因此PSO 算法在求解云資源調度問題時比GA 算法速度快。相比于ACO 算法，PSO 算法更容易獲取初始解，可以更有效地對云資源調度問題進行優化。綜合考慮，由于PSO 算法在分布式環境中計算速度較快，處理時間較短，本文使用了一種基于粒子群的優化算法對云資源調度問題進行求解。

在PSO 算法尋求最優解的過程中，存在收斂精度不高，容易陷入局部最優解，容易產生早熟收斂的問題，針對以上缺點和不足，本文提出了一種混合粒子群優化算法（re-randomization inertia weight orthogonal initialization particle swarm optimization，RIOPSO）。采用重新隨機化[11]的方法使粒子群能夠充分搜索解空間，避免粒子陷入早熟。采用實時更新慣性權重[12]的方法，控制粒子在搜索過程中的速度，防止陷入局部最優。本文還采用正交矩陣對粒子種群進行初始化[13]，使粒子群獲得有序的初始解，在粒子初始探索解空間時能夠更有效率。本文同時使用以上三種優化方法，使PSO 算法在搜索過程中，得到的解的質量更高，同時增強粒子的搜索能力，從而得到最優解。

1 相關工作

1.1 多目標問題

多目標問題（multi-objective problem，MOP）往往由于多個目標之間相互沖突，而無法獲得使每一個目標都達到最優狀態的最優解[14]。針對這一問題，將求解算法分為以下三種方式：

（1）基于帕累托支配的多目標進化算法[15]。由于目標函數的增多，最優解解集有時過于龐大，導致以該方法求解多目標問題時，容易產生消息溢出的問題[16]。

（2）基于性能指標的多目標進化算法[17]。在使用性能指標作為算法的進化的參考信息時，對于性能指標的計算過于復雜，導致運行時間較長[18]。

（3）基于分解的多目標進化算法[19]。將對多目標問題求解轉化為對多個單目標協同求解，引入分解的思想，將復雜的多目標問題簡單化。該算法求解效率高，解集性能較優。Zhang 等[20]提出的多目標進化算法（multi-objective evolutionary algorithm based on decomposition，MOEA/D）效果尤為顯著。

相比于其他兩種算法，基于分解的多目標進化算法，對于處理組合優化問題，有著較強的搜索能力。云資源調度的優化目標包括使總完成時間最短，使資源的消耗最少，滿足QoS 等，本文的主要研究目標是在有限資源下，使云資源調度能夠在時間-成本約束下完成調度目標。因此本文利用MOEA/D算法的分解思想，使用妥協模型，對時間和成本約束下的目標評價函數進行權重分解，根據權重占比，同步優化時間和成本的目標函數。

1.2 算法與性能指標

為了驗證本文提出的RIOPSO算法在求解多目標云資源調度的問題時，收斂性和多樣性都能夠得到保證，本文將使用NSGA-Ⅰ算法[21]、NSGA-Ⅱ算法[22]、NSGA-Ⅲ算法[23]和MOEA/D 算法[24]四種主流算法與本文提出的RIOPSO 算法進行對比實驗。

隨著多目標優化算法的提出，如何評價算法的優劣也成為一個重要的研究方向，在多目標優化算法解決多目標問題時，可以使用性能指標對算法性能進行量化比較。常用的性能指標可以分為：準確性度量指標、多樣性度量指標和綜合度量指標三類。

在上述算法求解多目標云資源調度問題時，使用兩個綜合度量指標，反向世代距離（inverted generational distance，IGD）[25]和超體積（hypervolume，HV）[26]指標，準確性度量指標覆蓋率（coverage-metric，CMetric）[27]指標，對算法的性能進行量化，并且通過量化后的性能對上述算法進行對比評價。

本文使用模糊數學模型，對不確定執行時間的多目標云資源調度問題進行求解。并且對如何能夠高效地找到最佳調度方案提出了優化算法。

2 模糊云資源調度問題

2.1 云資源調度模型

在云資源調度中，任務需要根據可行性算法在虛擬機上執行，并且每個任務只能在一個虛擬機上執行，但是虛擬機可以根據需要執行多個任務。現在有m個任務TASK={Task1,Task2,…,Taskm}，有n個虛擬機VM={Vm1,Vm2,…,Vmn}，虛擬機個數n遠小于任務個數m。

由于云資源調度中虛擬機和任務之間存在一對多的關系，可以將它們之間的映射關系表現為圖1 的形式。從圖中可以看出，每個任務只能在一個虛擬機上執行，每個虛擬機可以執行多個任務。如圖1 所示，代表一種調度方案Rk。

圖1是在云資源調度模型中用到的一些基本定義。

定義1timeij表示任務i在虛擬機j上執行的時間，其計算公式如下：

其中，taskSizei表示第i個任務的大小，vmSpeedj表示第j個虛擬機的處理速度，均在給定的范圍內隨機生成。

定義2vmTimej表示在虛擬機j上的任務執行時間，其計算公式如下：

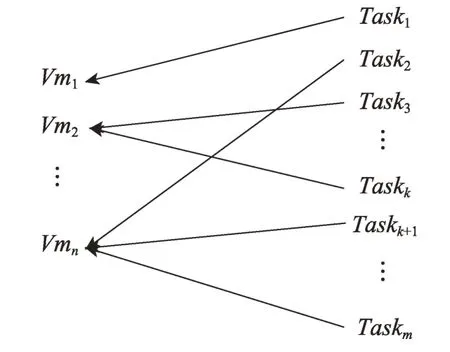
Fig.1 Task-VM mapping relationship圖1 任務-虛擬機的映射關系

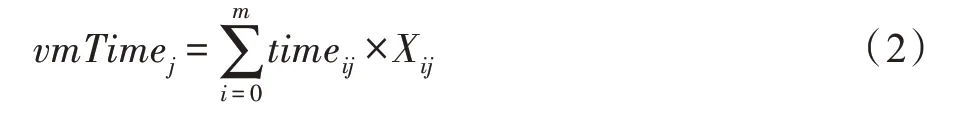
其中，Xij表示任務i是否在虛擬機j上執行，如果任務i在虛擬機j上執行，那么Xij=1，否則Xij=0。

定義3vmCostj表示在虛擬機j上的任務執行成本，其計算公式如下：

其中，costj表示單位時間內虛擬機j的執行成本，虛擬機執行成本由虛擬機的處理速度經過規則運算得到。

定義4Time(Rk)表示調度方案Rk的總的執行時間，由于任務的并發性，調度方案的總的執行時間就是執行時間最長的虛擬機的執行時間，其計算公式如下：

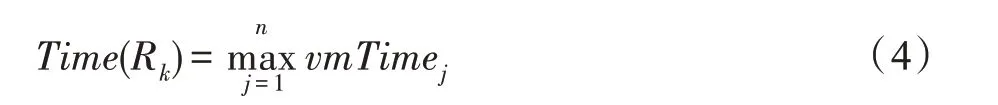
定義5Cost(Rk)表示調度方案Rk的總的執行成本，調度方案總的執行成本就是所有任務執行消耗的成本的和，其計算公式如下：

在求解最優調度方案時只考慮時間因素，那么時間約束函數為：

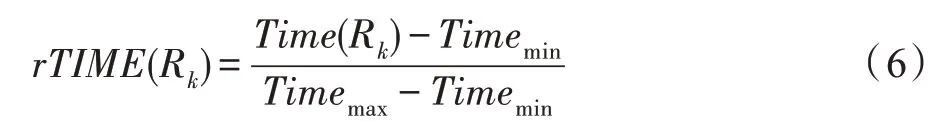
其中，Timemin、Timemax代表任務在虛擬機上執行的最短時間和最長時間。

如果只考慮成本因素時，成本約束函數為：

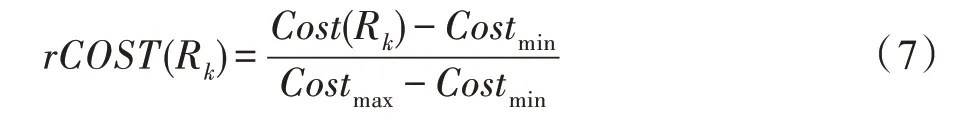
其中，Costmin、Costmax為任務執行所需的最低成本和最高成本。

由于只考慮時間因素或成本因素，考慮因素過于單一，并不能得到一個使得云資源提供者和云資源消費者都滿意的方案。文獻[28]提到，云資源提供者想要以較低的成本提供服務，而云資源消費者想要以較快的時間執行完任務。因此通過綜合考慮，為了達到能夠使云資源提供者和云資源消費者都能滿意的目的，提出時間-成本約束條件，將時間因素（6）和成本因素（7）通過式（8）將多目標問題轉化為單目標的問題。評價函數為：

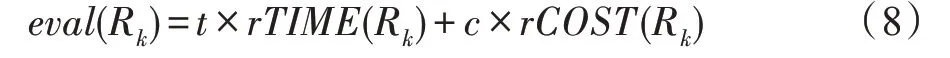
其中，t代表時間因子，c代表成本因子，本文通過改變t和c的值，來決定調度方案中時間因素和成本因素所占的比例，進一步控制時間和成本對于評價函數的影響。

時間-成本條件約束下的云資源調度模型為：

根據調度模型P，對每一種調度方案進行評價，得到最小的評價函數值，對應的調度方案就是最優調度方案。

2.2 模糊云資源調度模型

根據式（1）得到的是任務在虛擬機上執行的確定的時間。但是由于在實際執行過程中，任務的執行具有不確定性，本文使用三角模糊數對任務執行時間進行不確定表示。

使用三角模糊數給出任務執行時間的模糊范圍，通過式（10）和式（11）對任務在虛擬機上的執行時間的波動范圍進行上下范圍的判定。

任務執行時間的模糊下限：

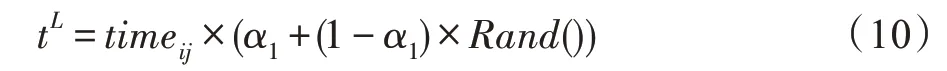
任務執行時間的模糊上限：

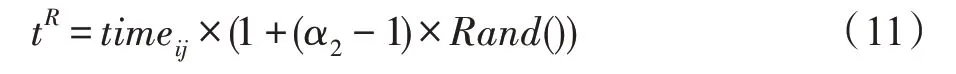
其中，Rand()表示在（0,1）中的隨機數，α1和α2分別表示上、下界的模糊系數。將任務的執行時間進行模糊之后，表示為，其中tL代表任務執行的樂觀時間，tM代表任務執行的最可能時間，tR代表任務執行的悲觀時間。

根據三角模糊數的線性特征和可分解性，使用模糊后的執行時間計算相應的評價函數值，將式（9）轉換為式（12）：

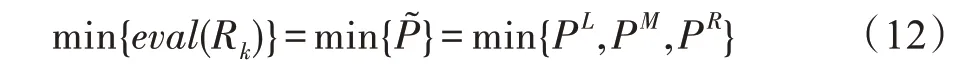
文獻[29]提出了一種判別規則，通過計算三角模糊數的平均值和標準差，判定誰的模糊性能更好。如果一個模糊數具有較高的平均值和較低的標準差，則認為該模糊數排序更高。

根據上述方法，可將確定的云資源調度模型轉化為不確定任務執行時間的模糊云資源調度模型。調度的目標轉化為對評價函數的平均值和標準差的計算，然后根據三角模糊數的加法運算和數乘運算，利用三角模糊數的特性，得出不確定任務執行時間下的云資源調度的問題模型，如式（13）所示。

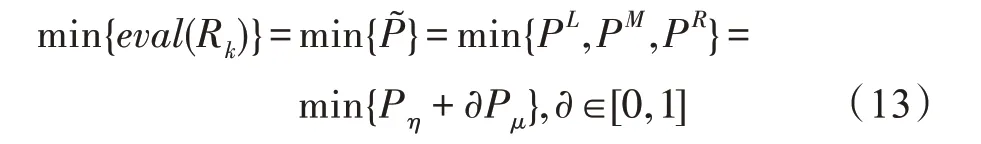
其中，Pη為模糊數的平均值，Pμ為標準差，?是對不確定度的加權系數。

3 RIOPSO 算法

3.1 PSO 算法分析

PSO 算法是模擬鳥類覓食行為的一種進化算法，通過迭代的方式，以個體最優尋找全局最優，從而得到最終的結果。本文使用不確定執行時間下的粒子群優化算法，對云資源調度問題進行求解。最優調度方案的判斷是通過評價函數的取值進行評價的。表1 是PSO 算法中需要用到的參數的定義。

Table 1 Parameter list表1 參數列表

在PSO 算法中，粒子可以模擬鳥類的覓食行為，在G維空間中進行尋優。在粒子群中有N個粒子，其中第i個粒子的位置為：

速度為：

粒子在迭代過程中通過對表1 中的速度的更新來進行位置的更新。

粒子群在尋優的過程中，通過比較評價函數的值找到個體最優和全局最優，之后對速度和位置進行迭代更新，其中在第k次迭代時，第i個粒子的個體最優值為pBesti，全局最優值為gBestk。粒子i的速度更新公式為：

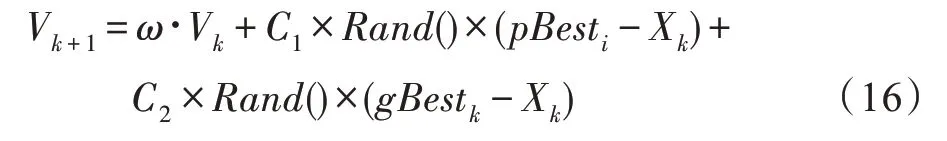
粒子的位移更新公式為：

如何使用PSO 算法解決云資源調度的問題，首先將PSO 算法中的粒子與云資源調度中的任務和虛擬機進行對應。粒子解空間的維數取決于云資源調度中的任務數。每一維的取值范圍就是云資源調度中被分配到的虛擬機數，即每一維的解對應的就是虛擬機的編號。粒子每一次的迭代更新的過程，粒子的位置就會發生相應的進化，就會產生一個新的進化粒子，產生一個如圖1 所示的新的任務和虛擬機之間的對應關系，一個新的調度方案。

對一個任務數為8，虛擬機數為3 的云資源調度來說，使用的PSO 算法中，粒子群中相應的粒子有8維，每一維的取值可以是0、1、2。對于任務和虛擬機之間的對應關系，表2 為粒子的一種可能表示方式。

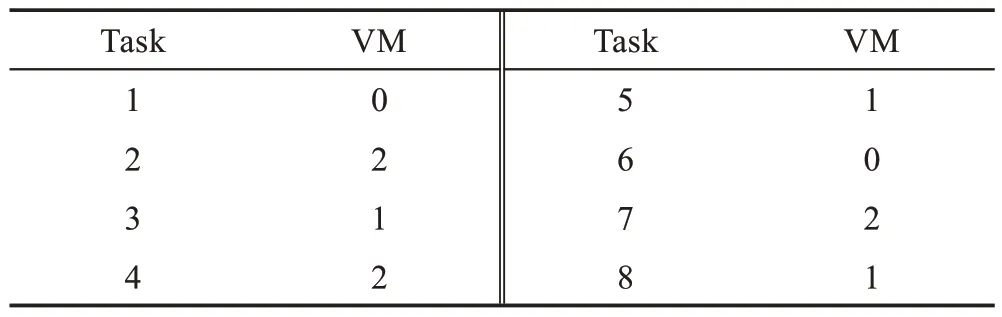
Table 2 Expression of a particle表2 某一粒子的表示

3.2 正交初始化

在PSO 算法中，粒子的尋優過程需要通過迭代來進行。粒子群的初始狀態對之后的尋優過程有著直接的影響，在粒子搜索的初始階段，初始解越有序越利于之后的粒子迭代搜索。在種群初始化時，要盡可能保證粒子均勻分布在解空間中，這就使得在初始化階段要滿足粒子具有各個方向的解。在PSO算法中，隨機初始化種群，并不能保證粒子能夠均勻分布在解空間中，有可能使粒子集中在一個區域，或者使粒子的相似程度過高，都不利于之后的尋優過程。在本文中使用正交矩陣初始化種群的方法，使整個種群均勻分布在可行解空間中。

當系統有Ele種元素，且每種元素都有Lev種水平，那么一共會有LevEle個組合數產生。如果在實驗中將這LevEle個組合全部進行實驗，當Lev和Ele很大時，會產生許多相似的組合，用這些組合做的實驗達不到好的效果，擬合度過高。因此構建正交矩陣G=Lrow(LevEle)，初始化種群，能夠篩選出均勻分布在解空間中的粒子，使用較少的組合進行實驗，從而使得粒子種群減小。這樣使用了較少的粒子，卻能夠達到更好的效果。其中，row 代表一共有多少組水平組合數，row 遠小于LevEle。

對任務數為4，虛擬機數為3 的云資源調度問題，使用正交初始化粒子種群的方式進行舉例。如果將每一個任務在每一個虛擬機上都執行，那么需要進行34=81 次的實驗。但是如果采用正交初始化的設計，只需要進行9 次實驗，就能夠找到代表性的解。而且隨著虛擬機數量和任務數量的增多，正交初始化就更能顯示出“均勻分散，齊整可比”的特點。

表3 就是使用正交矩陣，初始化虛擬機數為3，任務數為4 的云資源調度的分配方案。

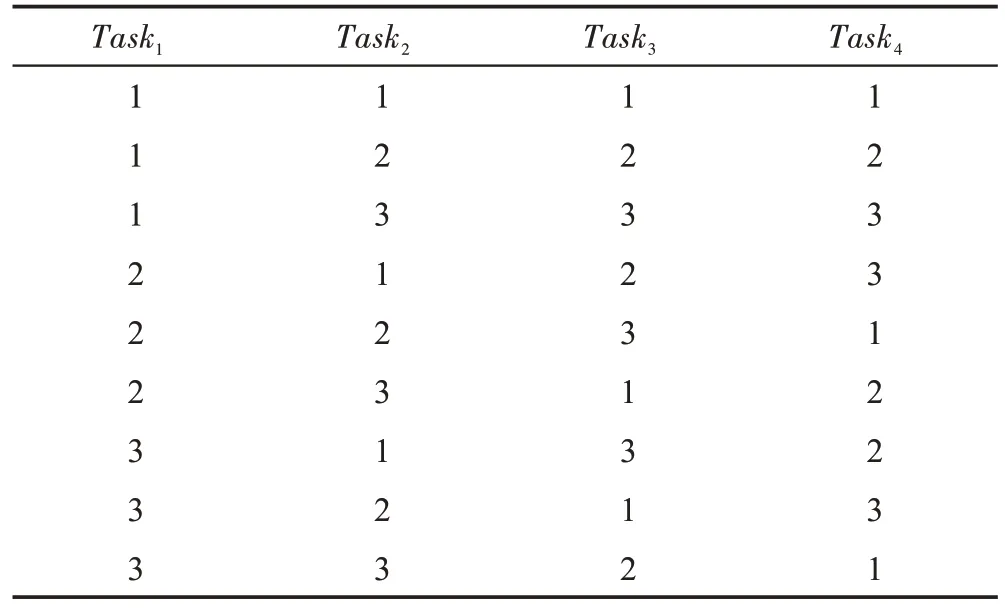
Table 3 Orthogonal initial population表3 正交初始種群

從表3 可知，使用正交矩陣初始化種群，只需9個初始解就可以均勻分布在解空間中。每一行代表一種調度方案，列數代表任務數，每一個數字代表執行任務選擇的虛擬機編號。

對于構建正交矩陣，首先需要確定基本列，然后根據基本列構建非基本列，基本列和非基本列的和就是需要構建的正交矩陣的列數，也就是一共需要被執行的任務數。基本列J滿足式（18），下面是創建正交矩陣的偽代碼。

算法1

步驟1構建基礎列

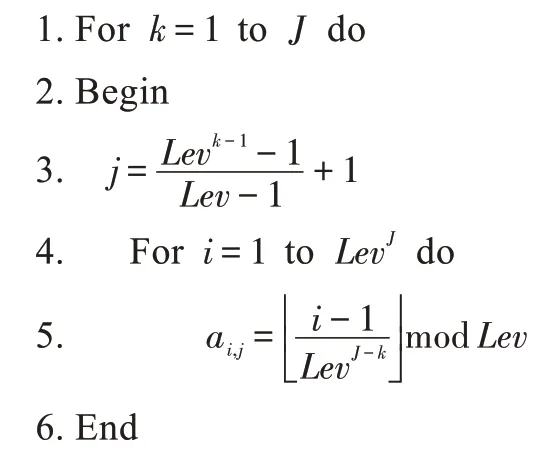
步驟2構建非基礎列

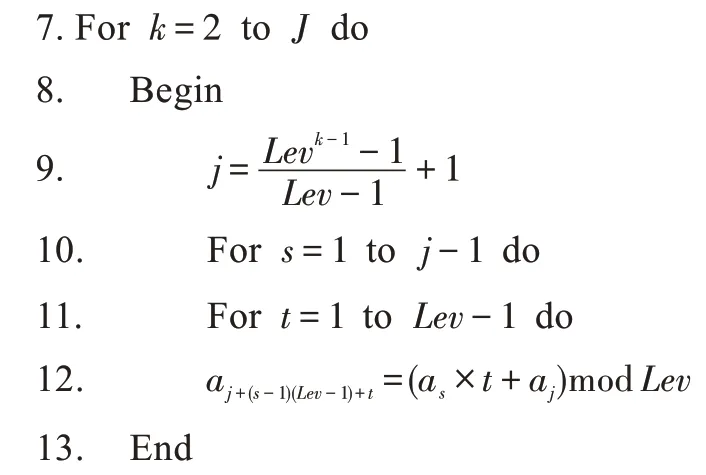
步驟3將ai,j進行加1

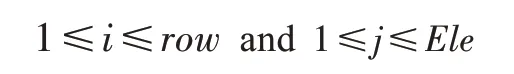
創建基本列和非基本列之后，已經將一個完整的正交矩陣構建完成，但是最終想要得到的是適合粒子群初始化的矩陣，就要對創建出來的矩陣進行列的取舍。算法2 得到最終的矩陣。

算法2

這樣就構建了用來初始化種群的正交矩陣。

3.3 重新隨機化

根據PSO 算法容易陷入局部最優的缺點，采用能夠使粒子跳出局部最優的重新隨機化的方法對粒子尋優能力進行優化，使粒子在解空間中能夠探索的范圍更大，尋優效率更高。通過計算方差的方式對粒子進行迭代更新，確保粒子能夠獲得更優的解。

根據式（19）得到適用于粒子種群的方差值，然后根據得到的方差對粒子群進行迭代更新。

在式（19）中，k代表當前迭代次數，A表示重新隨機化的有效初始值，S代表坡度，它控制粒子的搜索范圍。在搜索過程中，第一部分稱為大范圍搜索，即廣泛搜索，此時方差曲線的坡度較大，使得粒子能夠在遠離全局最優粒子gBest的搜索空間進行隨機搜索。第二部分稱為小范圍搜索，即精細搜索，此時方差曲線的坡度較小，粒子在靠近全局最優粒子gBest周圍進行隨機搜索。兩部分結合起來能夠使得最后粒子收斂到最優解，從而使得粒子能夠在全局范圍內進行搜索，跳出局部最優，搜索到最優解。M是對應方差曲線坡度中點的迭代次數，兩部分通過中間點M進行分割，中間點M決定廣泛搜索和精細搜索的搜索時間。

3.4 更新慣性權重

粒子在解空間中尋優時，粒子的收斂速度影響粒子在搜索過程中是否能收斂到當前最優狀態。粒子的慣性權重值是PSO 算法中的重要參數，通過調整粒子在每一次迭代過程中的慣性權重，來控制粒子的收斂速率。當粒子的慣性權重較大時，粒子搜索范圍增大，收斂速率過慢，不易得到精確的解；當慣性權重較小時，粒子的搜索范圍減小，收斂速度過快，容易陷入局部極值。根據粒子收斂過程中的這一特性，本文使用實時更新慣性權重的方式，和重新隨機化相結合，使粒子能夠探索到整個解空間的同時，控制粒子的收斂速率。

根據粒子在每一次迭代過程中評價函數的變化，對慣性權重值進行更新。當迭代之后的粒子的評價函數值變小，那么該粒子的慣性權重值將增加或者保持不變；如果該粒子的評價函數值變大，那么將對該粒子的慣性權重值進行減小。對應公式為式（20），對第i個粒子的慣性權重值進行實時更新。

其中，ωi(k)表示當前第i個粒子的慣性權重值，取值范圍為（0,1），S代表期望的評價函數值的范圍，ΔJi(k)代表該粒子當前評價值與前一個狀態評價值的差值。

在重新隨機化和更新慣性權重之后速度的更新由式（16）變為式（21）。

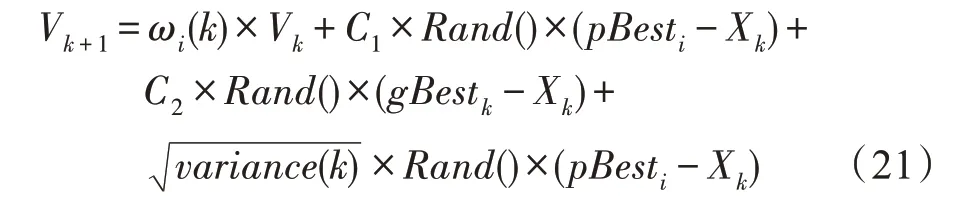
粒子的位置更新公式為：

其中，variance(k)就是重新隨機化中的方差，取值由式（19）決定。ωi(k)就是每一個粒子在每一次更新中的慣性權重值，取值由式（20）決定。

RIOPSO 算法的流程圖如圖2 所示。

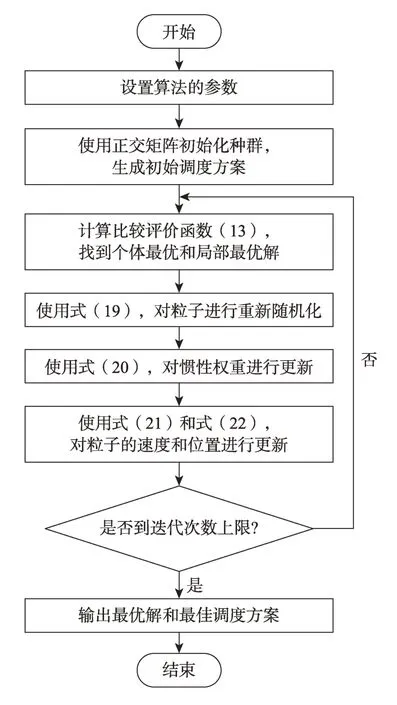
Fig.2 Algorithm flowchart圖2 算法流程圖

4 仿真實驗

4.1 數據的生成與參數的選擇

為了分析和比較本文提出的模型和算法的性能，在云計算仿真平臺Cloudsim 上進行仿真實驗。時間和成本對實驗的結果都有影響，本文將式（8）中的時間因子t和成本因子c都設置為0.5。本文采用文獻[30]的數據生成方法產生數據集，使生成的任務大小和虛擬機處理速度分別在范圍[3 000,130 000]和[300,1 300]之內。根據得到的任務的大小和虛擬機的處理速度，使用2.1 節中的計算方式，就可以得到任務在虛擬機上的執行時間和執行成本。

在RIOPSO 算法中，粒子群的速度、位置和慣性權重值的更新都是根據評價函數的取值是否變化，來進行迭代更新的。在參數設置中，個體學習因子C1和群體學習因子C2的取值，對實驗結果有所影響。當C1=1，C2=0 時，說明當前的粒子只受其個體最優值pBest影響，對當前的全局最優粒子的學習能力為0；而C1=0，C2=1 時，說明當前粒子的更新只受全局最優gBest的影響，對該粒子個體的學習能力為0。在本文中將個體學習因子C1和群體學習因子C2均設置為0.5。

本文實驗中各項參數設置如表4 所示。

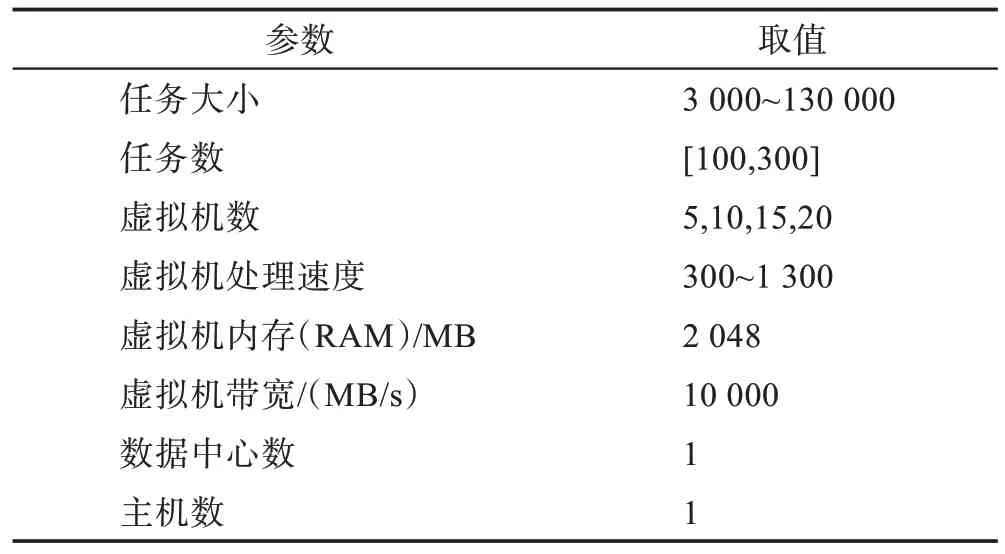
Table 4 Setting of experimental parameters表4 實驗參數的設置

在本文進行的實驗中，除算法改進策略不同外，均使用相同的數據集和實驗參數，在同一模型和同一環境下對云資源調度問題進行求解。

4.2 算法性能指標評價分析

使用算法NSGA-Ⅰ、NSGA-Ⅱ、NSGA-Ⅲ和MOEA/D 與本文提出的RIOPSO 算法求解云資源調度的問題。

（1）NSGA-Ⅰ算法。非支配排序遺傳算法，與遺傳算法相比在選擇算子執行之前，根據個體間的支配關系進行了分層。

（2）NSGA-Ⅱ算法。帶有精英保留策略的快速非支配多目標優化算法，采用了擁擠度比較的策略，是一種基于帕累托最優解的優化算法。

（3）NSGA-Ⅲ算法。在NSGA-Ⅱ算法的基礎上，提出一種參考點的選擇操作，代替NSGA-Ⅱ算法中的擁擠距離的選擇操作。

（4）MOEA/D 算法。一種基于分解的多目標進化算法。

使用上述算法解決云資源調度問題時，分別計算此時的IGD、HV 和C-Metric，以此量化各個算法的性能。

（1）IGD 是算法的綜合性能評價指標，對帕累托前沿上的解與算法獲得的解的最小距離進行計算。IGD 的值越小，說明算法得到的解分布越均勻，同時收斂性越好。

（2）HV 對非支配解覆蓋解空間的大小進行度量，HV 的值越大，證明該算法解的質量越高。

（3）C-Metric的計算基于帕累托解集的支配關系，該性能指標通過兩組帕累托前沿計算收斂性能。例如C(A,B)=1 表示B中的所有個體均被A中的支配，而C(A,B)=0 則表示B中的個體沒有被A支配。

表5 所示為五種算法的性能對比結果。性能指標結果使用均值進行記錄。

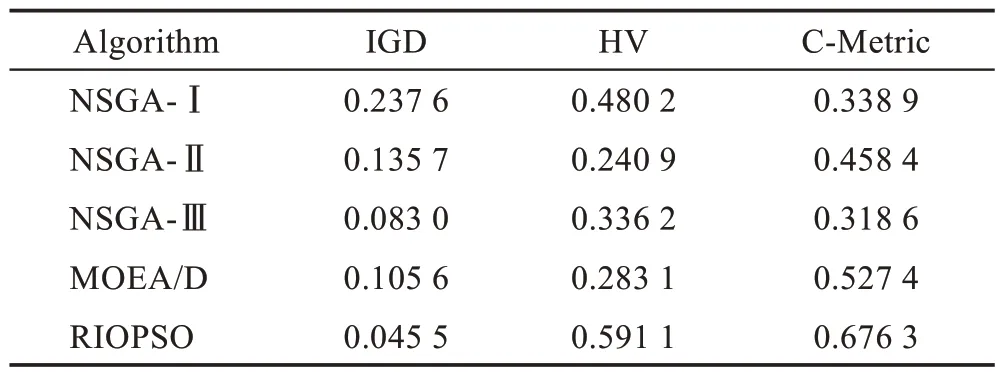
Table 5 Performance comparison of five algorithms表5 五種算法性能對比

從表5 中可以看出，RIOPSO 算法在IGD 性能比較中，具有最小的IGD 值，說明RIOPSO 算法獲得的解集分布均勻，能夠使種群更好地收斂到近似帕累托前沿面，綜合性能較好。通過超體積指標HV 看出，RIOPSO 算法獲得的非支配解與參考點之間構成的目標區域空間最大，相對于其他四種算法也具有最好的求解性能。從C-Metric 覆蓋率來看，RIOPSO算法中支配關系均少于其他幾種算法，這是由于RIOPSO 算法使用正交初始化的策略，在初始階段就獲得了較高質量的解集，從而獲得收斂性能更好的最優解。

綜上所述，使用本文算法改進策略在求解云資源調度問題時能夠在提高解質量的同時，使算法的綜合性能更好。

4.3 模型對比

由于在實際生活中，云資源調度的過程中存在任務執行的異步性和不確定性，本文使用三角模糊的方法，對問題模型進行了處理，使結果更加貼近實際。下面本文將對執行時間確定和不確定兩種情況的實驗結果進行比較。將每一個確定的執行時間進行三角模糊表示時，要對執行時間模糊之后的數進行左右范圍的確定，設置式（10）和式（11）中的參數α1=0.9,α2=1.2。相同的任務規模通過評價函數的平均值進行比較。圖3 為確定模型和模糊模型的對比結果。通過圖像可以看出，使用模糊模型，評價函數的值將會比確定模型下的評價函數的值高，這意味著對于不確定因素的考慮是很有必要的。如果忽略這些不確定的因素，將會導致實際效果和理論估計效果產生偏差而降低系統的效率。

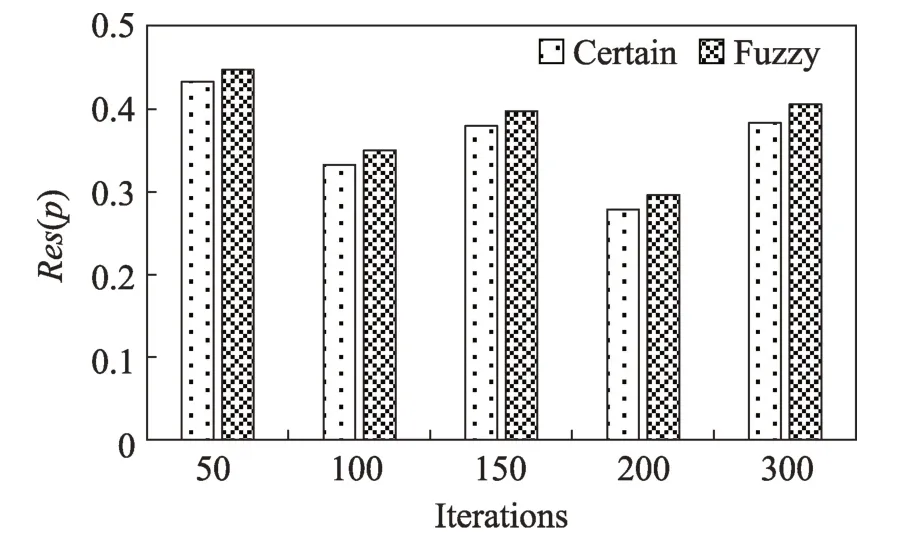
Fig.3 Model comparison圖3 模型對比

4.4 算法性能對比

為了分析本文提出的改進策略的具體優勢，將本文提出的RIOPSO 算法與其他三種算法進行對比分析。其中SPSO（re-randomization particle swarm optimization）算法使用了重新隨機化的策略[31]，沒有對問題的初始條件進行改進。SWPSO（re-randomization inertia weight particle swarm optimization）算法將重新隨機化和實時更新慣性權重進行結合[32]，初始化種群時使用的是隨機方法。OPSO（orthogonal initialization particle swarm optimization）算法使用正交初始化種群的方式[33]對PSO 算法進行優化。

為了能夠更直觀地看到本文算法的效率和更好的尋優能力，將本文提出的RIOPSO 算法，同上述提到的SPSO、SWPSO、OPSO 算法進行對比分析，在任務規模為100、200、300，虛擬機個數為5 的情況下，對四種算法分別進行尋優測試，并且進行記錄，實驗結果如圖4～圖6 所示。其中橫縱坐標分別代表迭代次數和算法對應的評價函數值。

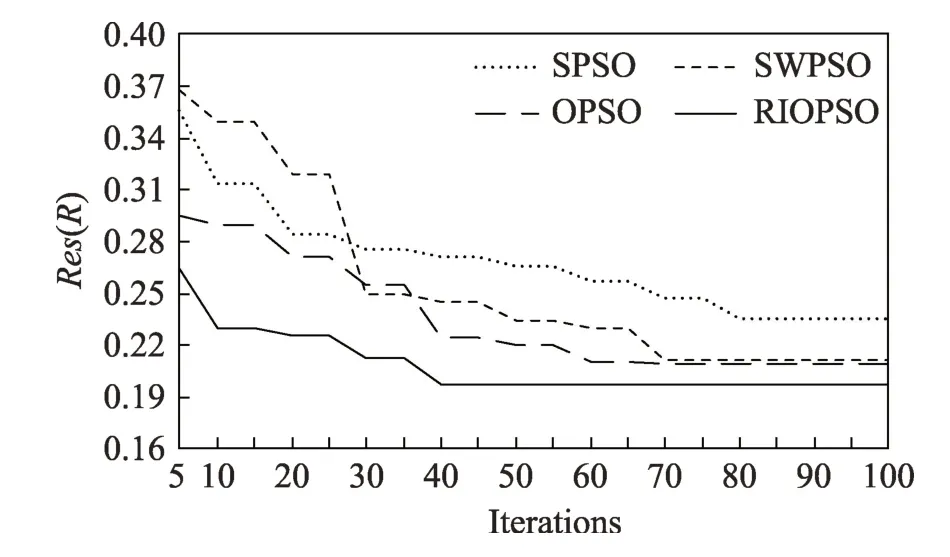
Fig.4 Comparison of algorithm optimization capabilities(100 tasks)圖4 算法尋優能力對比（100 個任務）

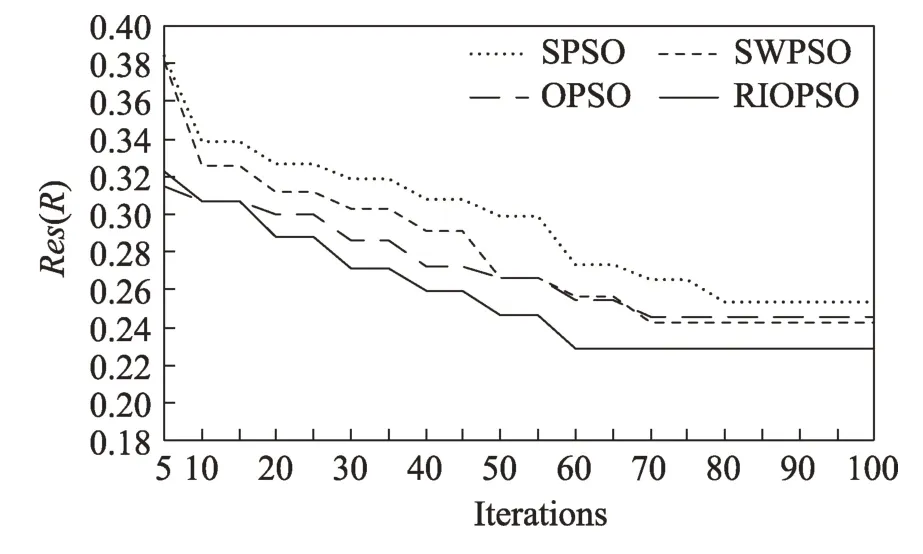
Fig.6 Comparison of algorithm optimization capabilities(300 tasks)圖6 算法尋優能力對比（300 個任務）

由圖4～圖6 可以發現OPSO 算法和RIOPSO 算法的初始評價函數均優于其他兩種算法，這是因為初始解的質量高，相應的也就提高了粒子群的搜索效率，證明了正交初始化策略的有效性。但是從迭代曲線中看出，由于粒子在搜索最優解的過程中可能會陷入局部最優狀態，OPSO 算法并不一定能獲得優于其他三種算法的解。相對比SPSO 算法，SWPSO算法和RIOPSO 算法在控制粒子搜索范圍的基礎上增加了對粒子搜索速度的控制，這使得粒子在搜索過程中能夠跳出局部最優，更好地收斂到全局最優解。從圖中還可以發現，無論是在大規模任務還是小規模任務中，綜合了以上三種策略的RIOPSO 算法，都能夠使用較少的迭代次數得出優于其他三種算法的解，減少了算法的運行迭代時間。因此RIOPSO 算法能夠具有尋優速度快，尋優能力強，尋優效果好的特點。

為了驗證在相同的任務數，不同的虛擬機數的情況中，RIOPSO 算法的能力，在4 個不同的數據集上進行了多次測試，任務和虛擬機的個數分別為（100,5），（100,10），（100,15），（100,20），實驗結果取平均值后如圖7 所示。其中橫坐標表示任務數為100 時對應的虛擬機的數目，縱坐標表示評價函數值。

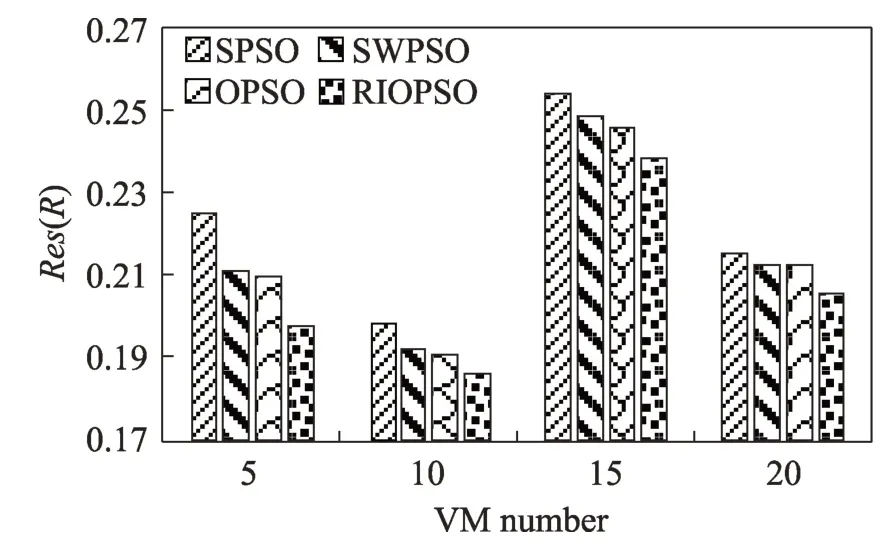
Fig.7 Comparison of optimization capabilities under same task scale圖7 相同任務規模下的尋優能力對比

通過圖7 可以看出，在相同任務數，不同虛擬機數的情況下，RIOPSO 還能夠搜索到比以上三種算法更優的解，得到更優的調度方案。

根據圖7中各個算法的評價函數值，建立了SPSO算法、SWPSO 算法、OPSO 算法的評價函數值大于RIOPSO 算法的評價函數值的相對差值百分比圖像。如圖8 所示，橫坐標代表虛擬機個數，縱坐標代表相對差值百分比。從圖中可以看出，無論虛擬機規模是多是少，相比于其他三種算法，RIOPSO 算法的尋優能力提升最高，進一步證明RIOPSO 算法的有效性。

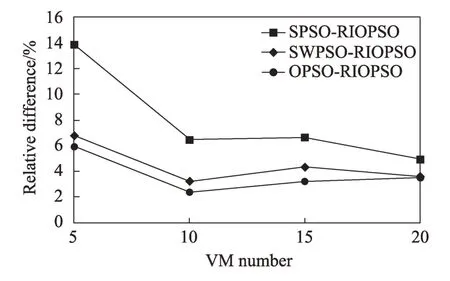
Fig.8 Comparison chart of algorithm optimization ability improvement圖8 算法尋優能力提升對比圖

在時間因子t和成本因子c均為0.5 時，使用以上四種算法對不同任務規模的調度模型進行多次實驗，對得到的調度方案中的任務運行總時間和任務運行總成本，分別計算取平均值，運行的虛擬機個數均為5。圖9 所示為四種算法運行的任務執行總時間，圖10 所示為任務執行的總成本。橫坐標均為任務規模，縱坐標分別為得到的調度方案中的任務總的執行時間和執行成本。

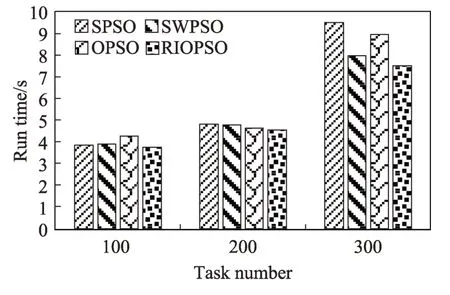
Fig.9 Total time of task execution圖9 任務執行總時間

從圖中可以看出，無論是任務執行的總時間還是任務運行的總成本，RIOPSO 算法都能夠得到最小的值。滿足關于得到最小執行時間和最少執行成本的雙目標的需要。

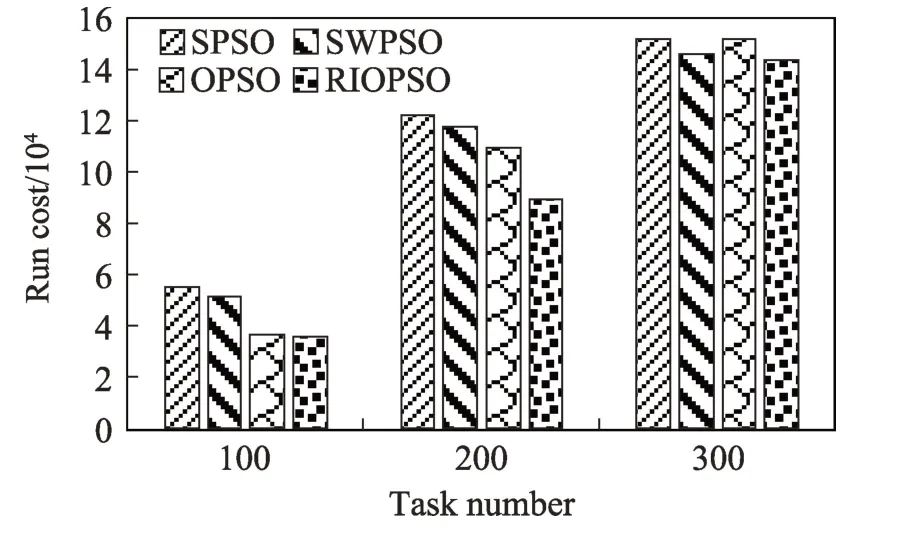
Fig.10 Total cost of task execution圖10 任務執行總成本

通過以上實驗得出，本文提出的RIOPSO 算法在尋優能力和尋優效率方面優于其他三種算法，并且在求解最優的云資源調度方案方面，能夠使任務的執行時間更短，執行成本更低，從整體上提高了云資源調度的綜合性能。

5 結束語

本文將降低任務的總完成時間和總執行成本作為主要目標，考慮不確定因素對任務的執行時間的影響，使用模糊的云資源調度模型，提出了一種改進的混合PSO 算法對云資源調度問題進行求解。在本文提出的RIOPSO 算法中，使用到了三種切實可行的策略：粒子群的正交初始化、粒子的重新隨機化、慣性權重的更新。三種策略分別在尋找最優解，跳出局部最優，提高粒子的收斂能力方面得到了很好的實驗效果。使用模糊模型使云資源調度更貼近實際應用。使用RIOPSO 算法對模糊云資源調度方面進行尋優，使得任務的執行時間更短，執行成本更低。相比較于單一的SPSO、OPSO、SWPSO 算法，使用RIOPSO 能夠得到更優的解，也更符合實際中的應用。