面向連續參數的多粒度屬性約簡方法研究

吳 將，宋晶晶,2+，程富豪，王平心，楊習貝,4

1.江蘇科技大學 計算機學院，江蘇 鎮江 212100

2.數據科學與智能應用福建省高校重點實驗室，福建 漳州 363000

3.江蘇科技大學 理學院，江蘇 鎮江 212100

4.江蘇科技大學 經濟管理學院，江蘇 鎮江 212100

粗糙集理論[1]最早是由波蘭學者Pawlak 提出的，這一理論近年來在數據挖掘、人工智能、決策分析等領域[2-4]受到了廣泛關注。在粗糙集理論與方法中，屬性約簡問題[5-10]一直是眾多學者關注的焦點。作為一種特征選擇機制，約簡的目的是獲得滿足給定約束條件的最小屬性子集，進而達到降低不確定性、提升學習器泛化性能等目的。在數據分析中，屬性約簡中的約束條件往往可以通過一些度量準則進行構造，如近似質量、條件熵等[6,8]。

經典粗糙集方法僅能處理符號型數據，但在解決實際應用問題時，連續型數據是廣泛存在的。因此已有諸多學者構建了很多拓展的粗糙集模型以用于分析及處理連續型數據：如基于高斯核函數的模糊粗糙集[10]和基于鄰域關系的鄰域粗糙集[5]。這兩者均可以視作是使用參數化的方法構造二元關系及相應的粗糙集模型。但值得注意的是，利用這些參數化粗糙集進行屬性約簡問題的研究時，會帶來諸如參數計算量過大等一系列問題。鑒于此，已有學者將參數視為粒度的表現形式[11-13]，對多粒度環境下的屬性約簡問題進行了初步探索。然而，已有的研究成果仍然存在一些可以提升的空間：（1）在多個參數所對應的多粒度結構下進行約簡求解時，一種常用的策略是針對于每一個參數，分別求解約簡。顯然，當參數體量較大時，這一過程會帶來較高的時間消耗。（2）在多個不同的參數下，可以得到多個約簡，當參數之間差異性較小時，這些約簡結果有可能存在較大的差異性。換言之，單個約簡一般只能表示某個粒度意義下滿足約束條件的最小屬性子集，而對于其他相鄰參數所對應的粒度，約簡的結果有可能大相徑庭。因此，多參數意義下的多個約簡結果并不具有普適性。

為了解決上述問題，本文從連續參數的視角出發，提出了多粒度屬性約簡的一種新模式，主要包括兩部分內容：首先在一個連續參數區間內，構造了多粒度屬性約簡的約束條件，然后利用前向貪心搜索策略，設計了求解多粒度約簡的算法。與多個參數意義下分別求解約簡的模式不同，連續參數下多粒度屬性約簡的目的不是分別針對每個參數進行約簡求解，而是根據多粒度約束條件求得一個約簡，進而有望降低約簡求解的時間消耗。

1 基礎知識

1.1 鄰域粗糙集

在粗糙集中，決策系統可以表示為一個二元組DS=，其中，U={x1,x2,…,xn} 是所有樣本構成的非空有限集合，稱為論域；AT是所有條件屬性的集合；d是決策屬性，用以描述樣本的標記。U/IND(d)={X1,X2,…,Xk}表示由決策屬性d所誘導出論域上的劃分，?Xp∈U/IND(d)，Xp表示具有相同標記的樣本所構成的第p個決策類。

在粗糙集理論中，信息粒化[14-19]的進程一般是通過利用條件屬性所提供的信息來構建二元關系，進而能夠對論域中的樣本進行區分。以鄰域粗糙集模型為例，可以通過在論域上使用鄰域關系[5]來進行信息粒化，鄰域關系的定義如下所示。

定義1給定決策系統DS=與半徑δ，?B?AT，鄰域關系可以定義為：

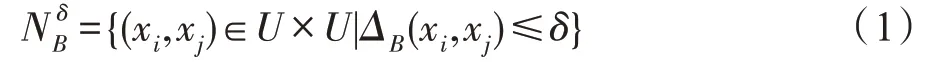
其中，ΔB(xi,xj)表示利用條件屬性子集B所提供的信息得到的樣本xi與xj之間的距離。

使用如式（1）所示的鄰域關系對論域進行信息粒化可得到所有樣本的鄰域，?xi∈U，xi的鄰域可以表示為δB(xi)={xj∈U|ΔB(xi,xj)≤δ}，δB(xi)中的樣本被視作與xi是不可區分的，而δB(xi)之外的樣本則被視作與xi是可區分的。因此，每個樣本的鄰域即表示了一個信息粒，所有樣本的信息粒的合集就是信息粒化的結果。一般來說，如果半徑δ較小，那么利用式（1）將會得到較細的信息粒化結果；反之，將會得到較粗的信息粒化結果。為了量化地描述信息粒化結果的粗細程度，可以使用如下定義所示的粒度概念。

定義2[13]給定決策系統DS=與半徑δ，?B?AT，粒度可定義為：

其中，|X|表示集合X的基數。

因為式（1）所示的鄰域關系滿足自反性，所以在定義2中，有成立。在特殊情況下：（1）當鄰域關系為ω={(xi,xi)∈U×U:?xi∈U} 時，可得到最細的信息粒，此時粒度取最小值1/|U|；（2）當鄰域關系為η={(xi,xj)∈U×U:?xi,xj∈U}時，可得到最粗的信息粒，此時粒度取最大值1。

定義3[8-9]給定決策系統DS=與半徑δ，?B?AT，d關于B的下近似集和上近似集可分別定義為：

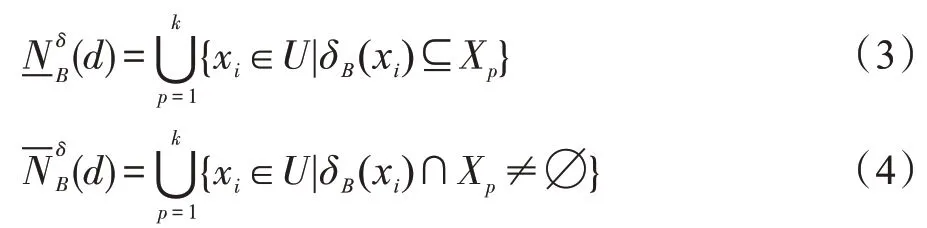
作為粗糙集理論中屬性約簡中常用的度量準則，近似質量的形式化描述如定義4 所示。

定義4[20]給定決策系統DS=與半徑δ，?B?AT，d關于B的近似質量可以定義為：

條件熵作為另一種常用的度量，它能反映條件屬性相對于決策屬性的鑒別能力。根據實際應用的不同，條件熵有很多定義的形式[17-19]，其中一種具有單調性的條件熵定義如定義5 所示。

定義5[21]給定決策系統DS=與半徑δ，?B?AT，d關于B的條件熵可以定義為：

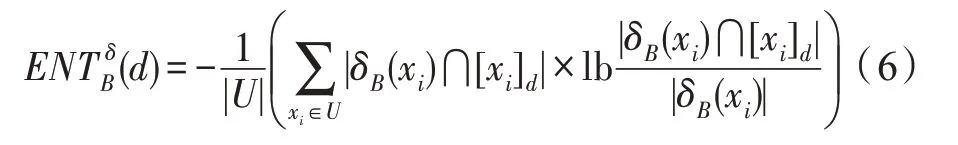
其中，[xi]d表示與樣本xi屬于同一決策類的樣本的合集。

條件熵的值越小，則條件屬性相對于決策屬性的鑒別能力越強。

1.2 多粒度屬性約簡

屬性約簡是粗糙集理論研究中的一個核心問題，其本質是去除條件屬性中的冗余和不相關屬性，以得到滿足給定約束條件的最小屬性子集。為了更深入地理解屬性約簡的本質，Yao 等人[6]從粒計算角度出發，給出了屬性約簡的形式化方法。但由于Yao等人提出的屬性約簡定義只適用于描述單個粒度下的約簡，而單粒度約簡無法為參數化粒度的選擇提供有力的支撐，且無法展現不同粒度所對應約簡的性能的變化趨勢[11]，因此，Jiang 等人[12]采用鄰域的方法，給出了一種多粒度屬性約簡的形式化描述方法，如定義6 所示。

定義6[12]給定決策系統DS=，一組半徑{δ1,δ2,…,δs}和關于δt(1 ≤t≤s)的約束條件，?B?AT，B={B1,B2,…,Bs}被稱為一個關于φ的多粒度約簡，?Bt∈B，當且僅當：

（1）Bt滿足約束條件；

顯然，定義6 所示的多粒度約簡是多個單粒度約簡的合集。其中，φ代表度量準則，可表示由近似質量構造的約束條件或者由條件熵構造的約束條件。當使用近似質量構造的約束條件時，為，此時每一單粒度約簡是一個能夠保證當前粒度下近似質量不會被降低的最小屬性子集Bt；當使用條件熵構造的約束條件時，φδt為，此時每一單粒度約簡是一個能夠保證當前粒度下條件熵不會被升高的最小屬性子集Bt。

目前，前向貪心搜索策略在約簡的求解問題中受到眾多學者的青睞，這一方法在每次迭代的過程中將屬性重要度最大的屬性加入到約簡集合中，直至所選擇的屬性子集滿足約束條件。鑒于此，可以采用如定義7 所示的形式對候選屬性進行評估。

定義7給定決策系統DS=與半徑δ，?B?AT，?ai∈AT-B，屬性ai相對于B的屬性重要度可定義為：

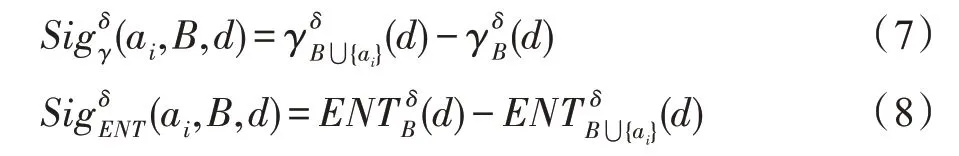
式（7）表示利用近似質量計算屬性重要度，若加入ai后近似質量的值越大，則說明ai的重要度越高；式（8）表示利用條件熵計算屬性重要度，若加入ai后條件熵的值越小，則說明ai的重要度越高。

實際上，定義6 所示的多粒度約簡是多個單粒度約簡的合集，因而多粒度約簡求解可通過重復單粒度約簡求解過程來實現。采用前向貪心搜索策略，運用定義7 所示的屬性重要度，可設計出如算法1 所示的多粒度約簡求解過程。

算法1離散參數下的多粒度約簡合集求解算法

利用算法1 求解多粒度約簡的時間復雜度為O(s×|U|2×|AT|2)，主要是因為：（1）在單個粒度下計算鄰域的時間復雜度為O(|U|2×|AT|2)，而在最壞的情況下，每個條件屬性都需要被評估且加入約簡集合中，即AT中沒有冗余的屬性，則單粒度下求解約簡的時間復雜度為O(|U|2×|AT|2)；（2）對于求解s個粒度下的約簡是將單粒度求解約簡的過程重復s次，因此求解多粒度約簡的時間復雜度為O(s×|U|2×|AT|2)。

2 連續參數意義下多粒度屬性約簡

不難發現，算法1 所示的多粒度約簡求解過程是在離散化參數的基礎上實現的，這種重復求解單個參數所對應約簡的策略，當參數體量過大時會導致求解約簡的時間消耗急劇增加。鑒于此，本文將提出一種基于連續參數的多粒度屬性約簡框架：給定參數區間[δ1,δs]，設計相應的約束條件求得約簡，期望用此約簡結果表示在整個區間[δ1,δs]下求得的各個多粒度約簡，而不再針對連續參數中的每一個參數進行求解約簡得到的多粒度約簡結果。

在連續參數下多粒度求解約簡的過程中，如何設計和求解約束條件φ是一個關鍵問題。從算法1中可以看出，多粒度約簡合集的求解是通過重復求解單粒度約簡來實現的。針對連續參數下約簡求解問題，在仔細分析粒度的公式（定義2）的基礎上，可以觀察到，對于給定的參數區間[δ1,δs]，利用最小參數δ1可獲得一個最細粒度，利用最大參數δs可獲得一個最粗粒度。因此，本文將使用最細粒度和最粗粒度下度量準則的融合策略來進行屬性約簡。

定義8給定決策系統DS=與一個半徑區間[δ1,δs]，?B?AT，B被稱為條件屬性AT的一個關于φ在連續參數下的約簡，當且僅當：

（1）B滿足約束條件；

（2）?B′?B,B′不滿足約束條件。

在定義8 中，與定義7 類似，其中，φ代表度量準則，可表示由近似質量構造的約束條件或者由條件熵構造的約束條件。但與定義7 不同，當使用由近似質量構造的約束條件時，且”，即定義8 給出的約簡是一個能夠保證在連續參數上，利用δ1和δs計算出的近似質量不會降低的最小屬性子集B；當使用由條件熵構造的約束條件時，為“且”，即定義8 給出的約簡是一個能夠保證在連續參數上，利用δ1和δs計算出的條件熵不會增大的最小屬性子集B。

運用定義8 和以上對約束條件的構造，可設計出如算法2 所示的連續參數下多粒度約簡求解算法。

算法2連續參數下的多粒度約簡求解算法

算法2 的時間復雜度為O(|U|2×|AT|2)。對于計算連續參數下的約簡，只需執行一次算法2，但對于算法1 而言，需要針對s個參數進行約簡的求解，此時算法1 將被執行s次。顯然，當s>1 時，算法2 求解多粒度約簡的時間復雜度小于算法1 求解多粒度約簡的時間復雜度，因此從這一角度來看，采用算法2 有望降低求解多粒度約簡的時間消耗。

3 實驗分析

為了驗證算法2 的有效性，在連續參數下求解多粒度的約簡，本文參考了文獻[7]中選取半徑區間的方法并使用了該文獻實驗的8 組數據。數據的基本描述如表1 所示。

文獻[7]在選取半徑和半徑區間的過程中，使用了100 個不同半徑δ=0.01,0.02,…,1.00，并計算了相應的近似質量。對于每一個數據集，選擇了近似質量大于0.1 的半徑區間，這主要是因為在粗糙集理論中，較小的近似質量對刻畫確定性的意義不大。使用該方法選取各個數據集的10 個半徑和半徑區間，具體描述如表2 所示。

值得注意的是，在連續參數下求得的一個多粒度約簡是保持近似質量不會降低或條件熵不會增大的最小屬性子集。但是，經過大量實驗發現，連續參數下求解多粒度約簡的約束是很嚴格的，不利于冗余屬性的刪除，故可通過控制閾值的方式來控制約簡的約束條件[19]。為了能夠更有效進行實驗對比分析，閾值ε的取值分別為5%和10%。故本次實驗中約簡的約束條件為：當使用由近似質量構造約束條件時，形如“且”；當使用由條件熵構造的約束條件時，形如“且”。為了驗證新提出算法的有效性，實驗采用了五折交叉驗證的方法。在上述的8 組數據集中，利用五折交叉驗證，分別計算了離散參數下和連續參數下求得約簡的時間消耗與約簡中屬性所提供的分類精度，其中在計算分類精度時使用的方法分別為K最近鄰算法（K-nearest neighbor，KNN）與支持向量機（support vector machine，SVM）。

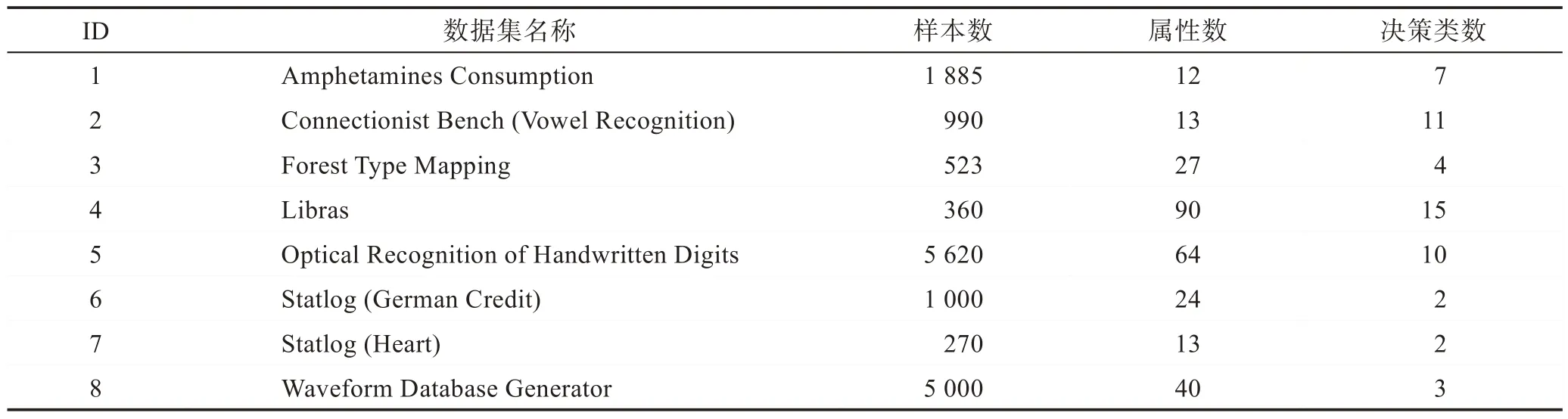
Table 1 Description of data sets表1 數據集描述

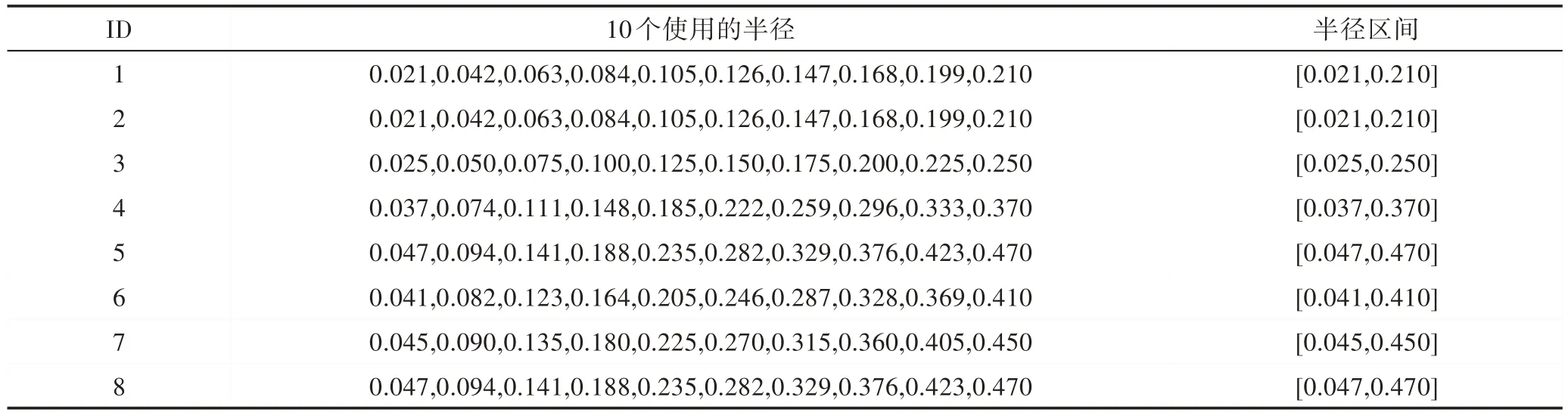
Table 2 Used radii and radii interval for data sets表2 數據集使用的半徑和半徑區間

3.1 時間消耗對比

觀察表3，不難得出以下結論：

（1）無論是使用算法1 還是算法2，相較于使用條件熵作為度量準則，在使用近似質量作為度量準則時，計算約簡的時間消耗較高。通過觀察實驗結果，認為主要是因為在使用近似質量作為度量時，約簡集合中包含屬性個數往往比使用條件熵時所求得的約簡集合中包含的屬性個數更多，此時帶來了屬性評估及屬性選擇迭代次數的增多。

（2）使用算法2 計算約簡的時間消耗顯著低于使用算法1 計算約簡的時間消耗。這是因為當給定10個半徑時，算法1 需要重復10 次前向貪心搜索策略，從而獲得多粒度下的約簡合集。然而，在連續參數下求解約簡只需要執行1 次就可以得到多粒度約簡結果。以“Amphetamines Consumption（ID：1）”數據集為例，使用近似質量作為度量時，約束條件的閾值為5%和10%的算法1 計算多粒度的約簡合集消耗的時間為34.975 7 s 和34.335 6 s，約束條件的閾值為5%和10%的算法2 計算多粒度約簡消耗的時間分別為7.796 5 s 和7.559 6 s。很明顯，算法1 的時間消耗大于算法2 的時間消耗。

（3）當約束條件的閾值設置為5%時，計算約簡的時間消耗一般要高于約束條件的閾值為10%時計算約簡的時間消耗。這是因為相對于閾值為5%的約束條件而言，閾值為10%時的約束更為寬松，因而約簡求解時屬性評估及屬性選擇的迭代次數減少了，帶來了更低的時間消耗。以“Statlog（German Credit）（ID：6）”數據集為例，在算法2 中使用條件熵作為度量時，約束條件的閾值為5%計算約簡的時間消耗為4.313 6 s，而約束條件的閾值為10%計算約簡的時間消耗為4.136 4 s。

3.2 分類精度對比

通過表4 和表5 展示的結果，不論采用KNN 分類器還是SVM 分類器，不難得出以下結論：

（1）無論是使用近似質量還是條件熵作為度量準則時，在大多數情況下，算法2 求得約簡中屬性所提供的分類精度比算法1 求得約簡中屬性所提供的分類精度高。這說明算法2 的連續參數下求得的多粒度約簡能夠帶來更好的分類性能。以“Libras（ID：4）”數據集為例，使用近似質量作為度量準則并將約束條件的閾值設為10%，采用KNN 分類器，算法1 求得約簡中屬性所提供的分類精度為0.715 8，算法2 求得約簡中屬性所提供的分類精度為0.775 0；采用SVM 分類器，算法1 求得約簡中屬性所提供的分類精度為0.443 6，算法2 求得約簡中屬性所提供的分類精度為0.602 8。

（2）在大多數情況下，約束條件的閾值為5%和10%求得約簡中屬性所提供的分類精度相差甚微。以“Forest type mapping（ID：3）”為例，算法2 使用近似質量作為度量準則時，使用KNN 分類器，約束條件的閾值為5%和10%求得約簡中屬性所提供的分類精度分別為0.858 5 和0.858 5。

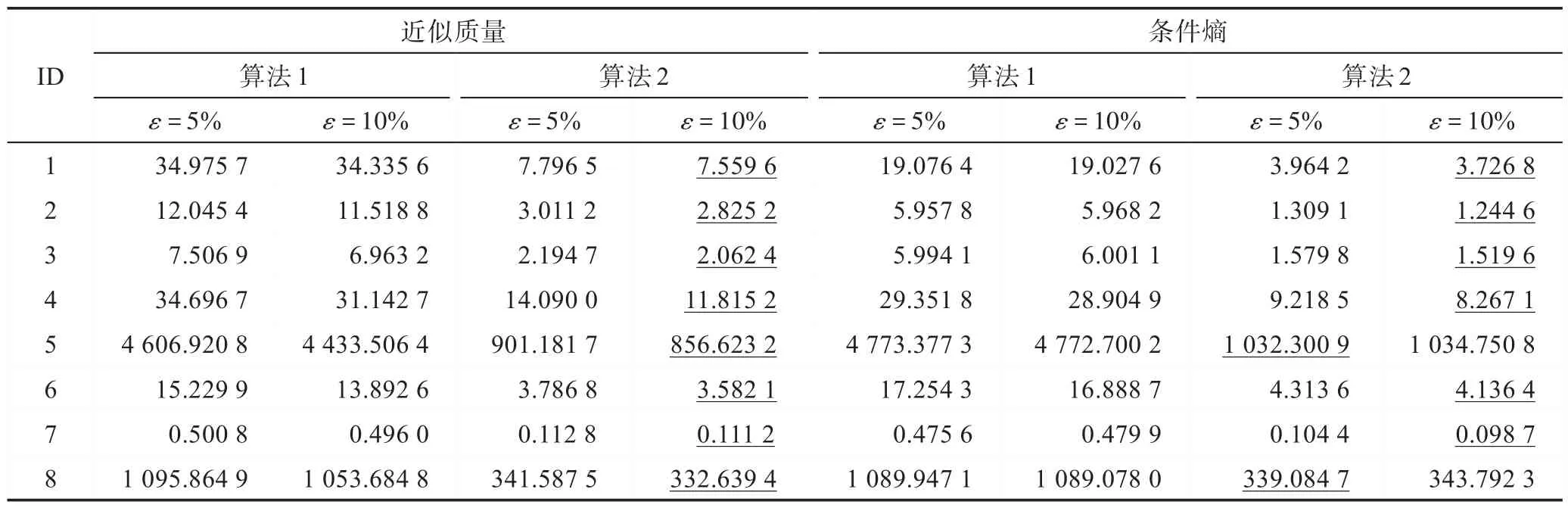
Table 3 Comparison of elapsed time of obtaining reduct表3 求解約簡的時間消耗對比 s

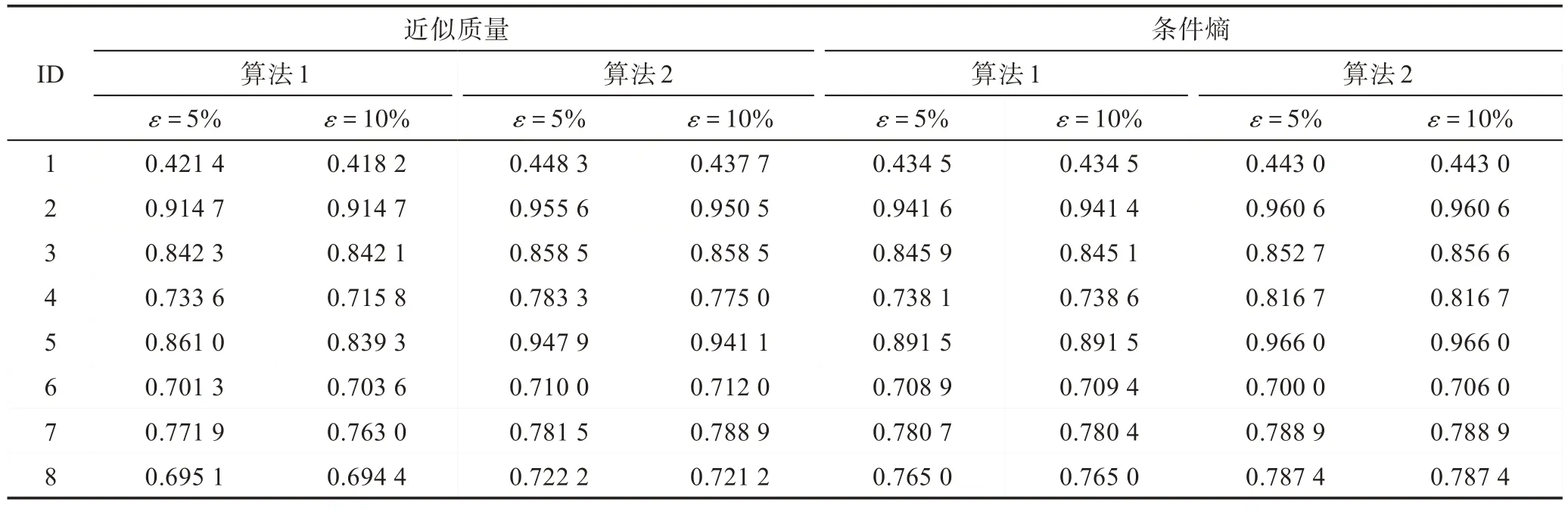
Table 4 Comparison of classification accuracies based on KNN表4 KNN 分類器下的分類準確率對比

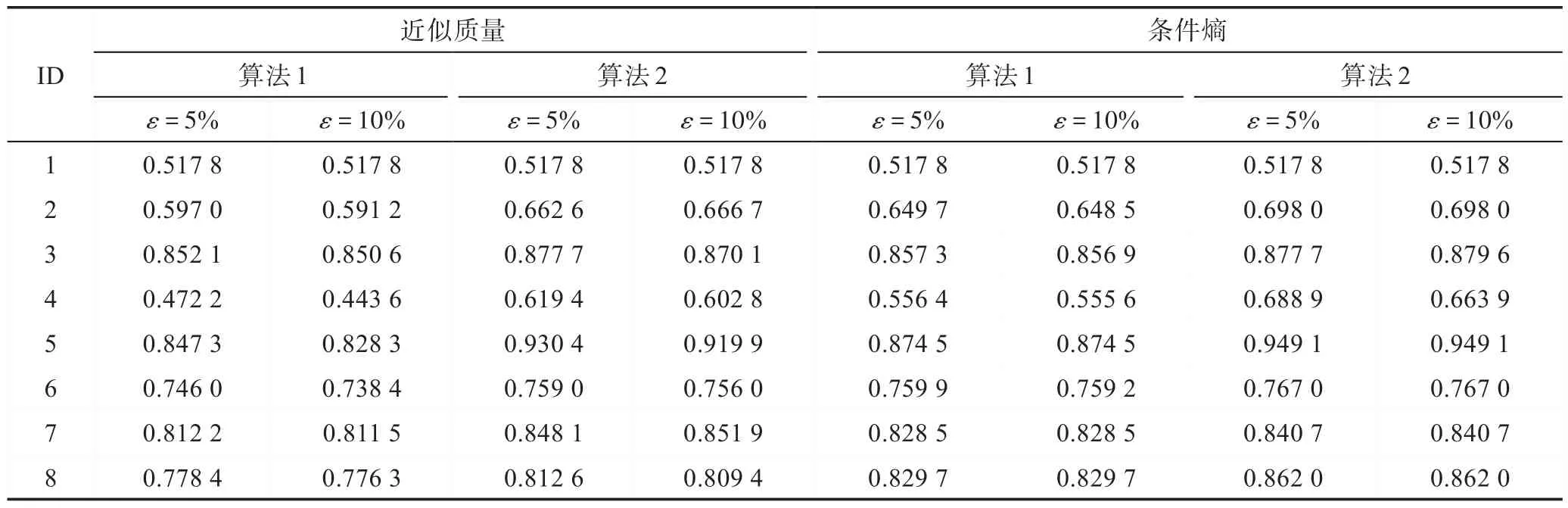
Table 5 Comparison of classification accuracies based on SVM表5 SVM 分類器下的分類準確率對比

4 結束語

與傳統約簡求解方法不同，為了降低多粒度約簡求解的時間消耗，本文提出了一個面向連續參數的多粒度屬性約簡框架。首先構造了連續參數下求解約簡的約束條件，然后利用前向貪心搜索策略，設計了求解連續參數意義下多粒度約簡的算法，最后將新提出的算法與離散參數意義下約簡的求解方法進行了對比。實驗結果表明，所提算法不僅能夠有效地降低約簡求解的時間消耗，而且所求得的約簡亦能夠提供滿意的分類性能。在本文工作的基礎上，可就以下的問題展開進一步的探討：

（1）文中僅使用近似質量和條件熵作為度量準則，未來工作中可以進一步考慮其他度量方式，如鄰域鑒別指數[8]、決策錯誤率[20]等。

（2）本文僅使用了鄰域粗糙集模型來構建連續參數下多粒度求解約簡的方法，可以將連續參數的思想拓展引入到其他的粗糙集模型，如模糊粗糙集模型。