基于鯨魚優(yōu)化算法的區(qū)域水資源優(yōu)化配置研究
田林鋼,楊 丹
(華北水利水電大學(xué),鄭州450046)
1 研究背景
水資源是人類賴以生存的重要資源,在人類的生產(chǎn)生活中發(fā)揮著重要的作用,是國(guó)家可持續(xù)發(fā)展的基礎(chǔ)[1-3]。隨著社會(huì)的不斷進(jìn)步和經(jīng)濟(jì)的快速發(fā)展,水資源需求與供給的矛盾日趨嚴(yán)重,水資源短缺與水環(huán)境惡化等問(wèn)題已經(jīng)成為社會(huì)發(fā)展的制約因素[4-7]。為解決區(qū)域水資源短缺問(wèn)題,通過(guò)水資源優(yōu)化配置,對(duì)區(qū)域有限的、不同形式的水資源進(jìn)行科學(xué)合理分配,實(shí)現(xiàn)水資源可持續(xù)利用和社會(huì)可持續(xù)發(fā)展。
目前國(guó)內(nèi)水資源優(yōu)化配置研究受到學(xué)術(shù)界的廣泛關(guān)注,研究方法正逐步趨于成熟[8,9]。沙金霞等應(yīng)用粒子群算法實(shí)現(xiàn)了引大濟(jì)湟工程受水區(qū)在不同規(guī)劃水平年下的水資源優(yōu)化配置[10];曾萌等運(yùn)用魚群算法解決了廣東省的水資源分配問(wèn)題[11];潘俊等以沈陽(yáng)市為實(shí)例分析,使用遺傳算法對(duì)水資源量進(jìn)行優(yōu)化配置[12];劉玒玒等運(yùn)用蟻群算法實(shí)現(xiàn)了黑河流域的水資源配置[13]。這些算法均在水資源優(yōu)化配置中得到應(yīng)用,但存在收斂速度較慢,易陷入局部最優(yōu)等問(wèn)題。鑒于此,本文將鯨魚優(yōu)化算法與水資源優(yōu)化配置問(wèn)題相結(jié)合,該算法具有收斂速度快、收斂精度高和全局尋優(yōu)能力強(qiáng)等特點(diǎn)[14]。以河南省某縣為例,以經(jīng)濟(jì)效益、社會(huì)效益和生態(tài)效益最優(yōu)為目標(biāo),構(gòu)建水資源優(yōu)化配置模型,利用鯨魚優(yōu)化算法求解出該縣不同規(guī)劃年(2025年和2030年)的水資源優(yōu)化配置方案,以期實(shí)現(xiàn)該區(qū)域水資源合理開發(fā)利用,使該區(qū)域的經(jīng)濟(jì)社會(huì)得到協(xié)調(diào)發(fā)展。
2 鯨魚優(yōu)化算法
鯨魚被認(rèn)為是世界上最大的哺乳動(dòng)物,成年鯨魚可以達(dá)到30 m 長(zhǎng),180 t 重。研究表明,鯨魚大腦的特定區(qū)域內(nèi)有著類似于人類的梭形細(xì)胞,這些細(xì)胞負(fù)責(zé)人類的判斷、情感和社會(huì)行為。換言之,梭形細(xì)胞使鯨魚區(qū)別于其他生物[15]。2016年,澳大利亞學(xué)者Seyedali Mirjalili 和Andrew Lewis 提出了一種新型群體智能優(yōu)化算法——鯨魚優(yōu)化算法(Whale Optimization Algorithm,WOA)[16]。該算法受座頭鯨捕食行為的啟發(fā),對(duì)座頭鯨群體的收縮包圍、螺旋式位置更新和隨機(jī)捕獵機(jī)制進(jìn)行模擬,其數(shù)學(xué)模型包括環(huán)繞式捕食、泡泡網(wǎng)捕食和搜索捕食3 個(gè)階段。
2.1 環(huán)繞式捕食
在環(huán)繞式捕食中,座頭鯨能識(shí)別獵物的位置并對(duì)其進(jìn)行包圍。假設(shè)當(dāng)前最優(yōu)位置為目標(biāo)獵物位置,在定義了最優(yōu)位置之后,其他鯨魚個(gè)體會(huì)朝著最優(yōu)位置不斷更新它們的位置。其位置更新的表達(dá)式為:
式中:t為當(dāng)前迭代次數(shù)和為系數(shù)向量為當(dāng)前鯨群個(gè)體的最優(yōu)位置為當(dāng)前鯨群個(gè)體的位置。
的計(jì)算公式為:

2.2 泡泡網(wǎng)捕食
根據(jù)座頭鯨的泡泡網(wǎng)捕食行為,建立如下兩種機(jī)制的數(shù)學(xué)模型。
(1)收縮包圍機(jī)制:該行為是通過(guò)減小參數(shù)來(lái)實(shí)現(xiàn)的。隨著的減小而減小,即的取值范圍是[-a,a]。當(dāng)?shù)娜≈捣秶冢?1,1]時(shí),鯨魚個(gè)體的新位置可以定義在當(dāng)前鯨群個(gè)體位置和最優(yōu)位置之間的任意位置。
(2)螺旋式位置更新機(jī)制:首先計(jì)算鯨魚個(gè)體和獵物(當(dāng)前最優(yōu)位置)之間的距離,然后在鯨魚個(gè)體和獵物(當(dāng)前最優(yōu)位置)的位置之間建立一個(gè)螺旋數(shù)學(xué)模型,以模擬座頭鯨的螺旋形運(yùn)動(dòng)。其數(shù)學(xué)模型為:
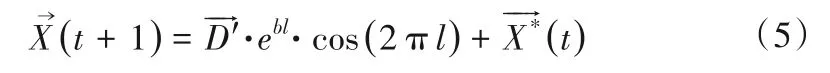
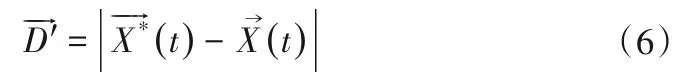
座頭鯨在收縮包圍獵物的同時(shí),也沿著螺旋形路徑運(yùn)動(dòng)。為了模擬這種行為,假設(shè)收縮包圍機(jī)制和螺旋式位置更新機(jī)制的更新概率相同,均為50%。其數(shù)學(xué)模型為:
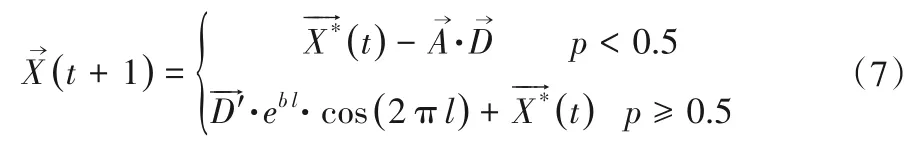
式中:p為[0,1]之間的隨機(jī)數(shù)。
2.3 搜索捕食
搜索捕食是通過(guò)的大小來(lái)搜索獵物的。在搜索捕食過(guò)程中,鯨魚個(gè)體會(huì)根據(jù)彼此的位置進(jìn)行隨機(jī)搜索獵物。因此,設(shè)定迫使鯨魚個(gè)體遠(yuǎn)離獵物,搜索其他更合適的獵物。這種機(jī)制以增強(qiáng)算法的搜索捕食能力,使該算法能進(jìn)行全局搜索。其數(shù)學(xué)模型如下:
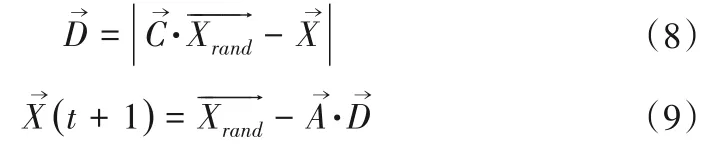
3 實(shí)例分析
3.1 研究區(qū)概況
某縣位于河南省西北部,地勢(shì)西高東低,自西向東傾斜,縣域面積805 km2,屬暖溫帶大陸型季風(fēng)氣候,年平均降雨量575.10 mm。由于該縣經(jīng)濟(jì)在快速發(fā)展階段,水資源的開發(fā)利用呈快速增長(zhǎng)趨勢(shì),導(dǎo)致整個(gè)區(qū)域水資源量短缺,供需矛盾突出,以及經(jīng)濟(jì)發(fā)展與水資源協(xié)調(diào)不夠等一系列水資源問(wèn)題。因此,對(duì)該區(qū)域的水資源進(jìn)行合理配置,實(shí)現(xiàn)不同水源和用水部門之間的供需水量平衡。
3.2 供需水量預(yù)測(cè)
該縣供水水源主要包括地表水(沁河水、黃河水、南水北調(diào)水以及其他地表水)、地下水和再生水,不同水平年的可供水量預(yù)測(cè)結(jié)果見表1。
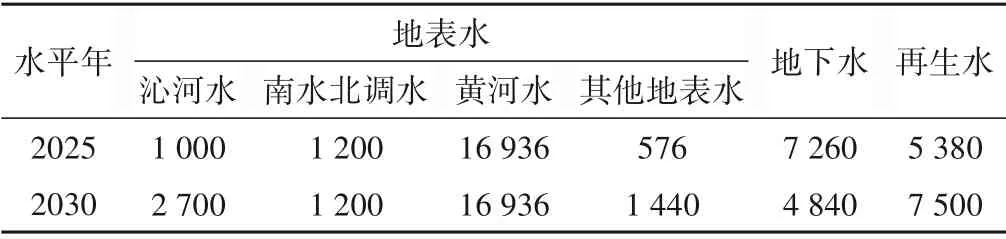
表1 不同水平年的供水量預(yù)測(cè)結(jié)果 萬(wàn)m3Tab.1 Prediction results of water supply in different level years
該縣用水部門主要包括生活用水、農(nóng)業(yè)用水、工業(yè)用水、第三產(chǎn)業(yè)用水和生態(tài)用水。以2017年為現(xiàn)狀基準(zhǔn)年,采用定額法預(yù)測(cè)2025年與2030年該縣各用水部門的需水量,具體結(jié)果見表2。
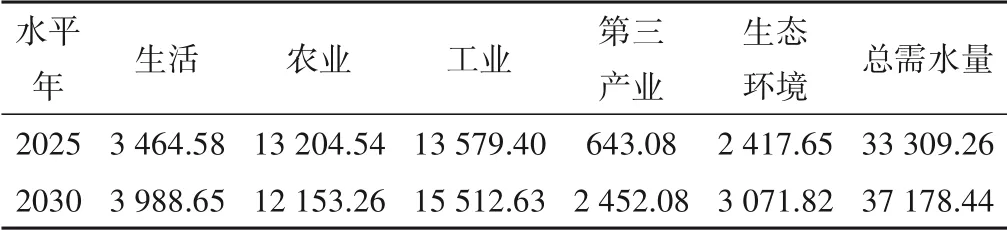
表2 不同水平年的需水量預(yù)測(cè)結(jié)果 萬(wàn)m3Tab.2 Prediction results of water demand in different level years
3.3 水資源優(yōu)化配置模型
3.3.1 目標(biāo)函數(shù)
(1)經(jīng)濟(jì)效益目標(biāo)。以區(qū)域供水經(jīng)濟(jì)效益最大來(lái)表示:
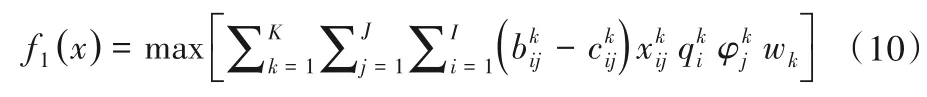
(2)社會(huì)效益目標(biāo)。以區(qū)域總?cè)彼孔钚?lái)表示:
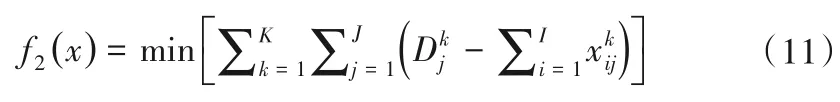
(3)生態(tài)效益目標(biāo)。以區(qū)域重要污染物化學(xué)需氧量(COD)排放總量最小來(lái)表示:
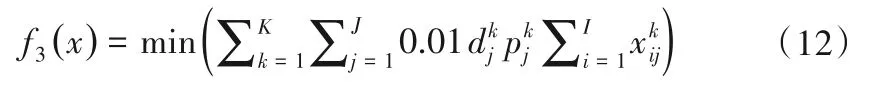
3.3.2 約束條件
(1)供水能力約束。k子區(qū)i水源向所有用戶的供水總量應(yīng)不大于其可供水量:

(2)需水能力約束。水源向用戶所分配的水量應(yīng)介于用戶需水量上下限之間:

式中:L(k,j)、H(k,j)分別為k子區(qū)j用戶需水量的上限、下限。
(3)廢水污染物質(zhì)量濃度約束。k子區(qū)j用戶排放的廢水中重要污染物(COD)的濃度應(yīng)在國(guó)家允許的排放指標(biāo)內(nèi),且排放的重要污染物總量應(yīng)不超過(guò)該區(qū)域的最大允許排放量:
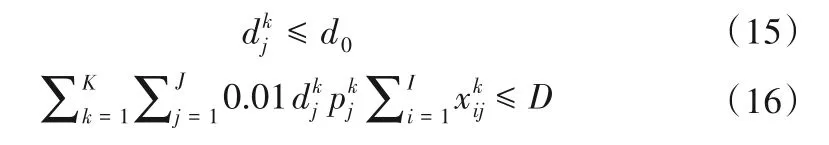
式中:d0表示在各行業(yè)中國(guó)家標(biāo)準(zhǔn)規(guī)定所排放的重要污染物(COD)質(zhì)量濃度,mg/L;D表示區(qū)域內(nèi)最大允許排放重要污染物的總量。
(4)變量非負(fù)約束。

3.3.3 模型參數(shù)確定
(1)權(quán)重確定。采用層次分析法和熵權(quán)法組合賦權(quán),確定經(jīng)濟(jì)、社會(huì)和生態(tài)環(huán)境3 個(gè)效益目標(biāo)權(quán)重,分別為0.47、0.30、0.23。
(2)供水效益系數(shù)。基于居民生活用水優(yōu)先序最高的原則,結(jié)合某縣及周圍地區(qū)的實(shí)際情況,生活供水效益系數(shù)取0.05 萬(wàn)元/m3。2025年農(nóng)業(yè)供水效益系數(shù)0.002 6 萬(wàn)元/m3,工業(yè)供水效益系數(shù)取0.018 2 萬(wàn)元/m3,第三產(chǎn)業(yè)供水效益系數(shù)取0.200 0 萬(wàn)元/m3;2030年農(nóng)業(yè)供水效益系數(shù)0.004 5 萬(wàn)元/m3,工業(yè)供水效益系數(shù)取0.025 0 萬(wàn)元/m3,第三產(chǎn)業(yè)供水效益系數(shù)取0.153 8 萬(wàn)元/m3。由于城市生態(tài)環(huán)境與居民生活密切相關(guān),故取生態(tài)供水效益系數(shù)等于生活供水效益系數(shù),取0.05 萬(wàn)元/m3。
(3)供水費(fèi)用系數(shù)。費(fèi)用系數(shù)參考該縣水價(jià)及稅費(fèi)征收標(biāo)準(zhǔn),確定生活用水費(fèi)用系數(shù)2.35 元/m3、農(nóng)業(yè)用水費(fèi)用系數(shù)0.40元/m3、工業(yè)用水費(fèi)用系數(shù)2.90 元/m3、第三產(chǎn)業(yè)用水費(fèi)用系數(shù)3.60 元/m3、生態(tài)用水費(fèi)用系數(shù)2.35 元/m3。
(4)供水次序系數(shù)。供水次序系數(shù)反映k子區(qū)i水源相比于其他水資源優(yōu)先使用程度的一種度量。水源供水次序系數(shù)參考下式確定[17]:
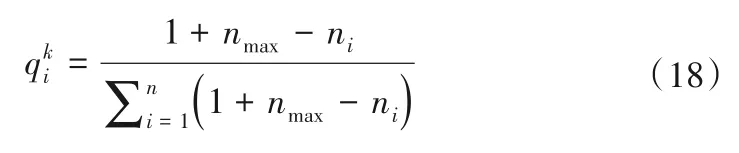
式中:ni為i水源供水次序序號(hào);nmax為最大水源供水序號(hào)。
基于某縣各供水水源的實(shí)際情況及各用水部門用水的重要程度,確定某縣水源的供水次序?yàn)椋浩渌乇硭⑶吆铀⒛纤闭{(diào)水、黃河水、地下水、再生水。由上式確定各水源供水次序系數(shù)分別為:0.29、0.24、0.19、0.14、0.10、0.05。
(5)用水公平系數(shù)。參考某縣各用水部門的重要程度,得到各用水部門的先后次序?yàn)椋荷钣盟⑸鷳B(tài)用水、工業(yè)用水、第三產(chǎn)業(yè)用水和農(nóng)業(yè)用水。參照供水次序系數(shù)的計(jì)算公式,計(jì)算得到各用戶的用水公平系數(shù)分別為0.33、0.27、0.20、0.13、0.07。
(6)鯨魚優(yōu)化算法參數(shù)設(shè)置。鯨魚種群數(shù)目N=150,最大迭代次數(shù)tmax=900。
3.3.4 模型求解過(guò)程
在建立以經(jīng)濟(jì)、社會(huì)和生態(tài)效益為目標(biāo)函數(shù)的水資源優(yōu)化配置模型和確定相關(guān)參數(shù)后,利用鯨魚優(yōu)化算法對(duì)模型進(jìn)行求解,具體求解步驟如下:
(1)隨機(jī)產(chǎn)生N只鯨魚作為初始種群,初始化算法參數(shù)和最大迭代次數(shù)tmax。
(2)以河南省某縣為例,根據(jù)經(jīng)濟(jì)、社會(huì)和生態(tài)環(huán)境3 個(gè)目標(biāo)函數(shù)確定的權(quán)重,將多目標(biāo)問(wèn)題轉(zhuǎn)換為單目標(biāo)問(wèn)題,然后計(jì)算每只鯨魚個(gè)體的適應(yīng)度值,找到當(dāng)前適應(yīng)度值最佳的鯨魚個(gè)體。
(3)進(jìn)入算法主循環(huán)過(guò)程,當(dāng)p<0.5 時(shí),若利用公式(1)和(2)更新當(dāng)前鯨魚個(gè)體位置;若利用公式(8)和(9)更新鯨魚個(gè)體位置。當(dāng)p≥0.5 時(shí),利用公式(5)和(6)更新鯨魚個(gè)體位置。
(4)計(jì)算更新后每只鯨魚個(gè)體的適應(yīng)度值,找到全局最優(yōu)的鯨魚個(gè)體。
(5)判斷算法是否滿足終止條件,若滿足,則輸出最優(yōu)鯨魚個(gè)體的位置及其對(duì)應(yīng)的適應(yīng)度值;否則,令t=t+1,轉(zhuǎn)到步驟(3)繼續(xù)進(jìn)行算法迭代。
3.4 結(jié)果與分析
通過(guò)結(jié)合某縣的實(shí)際情況,以及水資源優(yōu)化配置模型的相關(guān)參數(shù),利用Matlab 軟件求解出該縣不同水平年的水資源優(yōu)化配置結(jié)果。具體計(jì)算結(jié)果和供需平衡關(guān)系見表3和表4。
(1)配水量分析。分析表3和表4可以看出,2025年某縣各用水部門按配水比例依次排序?yàn)楣I(yè)、農(nóng)業(yè)、生活、生態(tài)、第三產(chǎn)業(yè),該順序與2025年某縣各用水部門預(yù)測(cè)需水量的結(jié)果一致。2030年各用水部門排序結(jié)果與2025年相同,符合該縣地區(qū)的實(shí)際情況。從配水比例看,2030年相比于2025年,農(nóng)業(yè)配水有所減少,生活、生態(tài)、工業(yè)和第三產(chǎn)業(yè)配水增加,該結(jié)果符合需水預(yù)測(cè)結(jié)果。
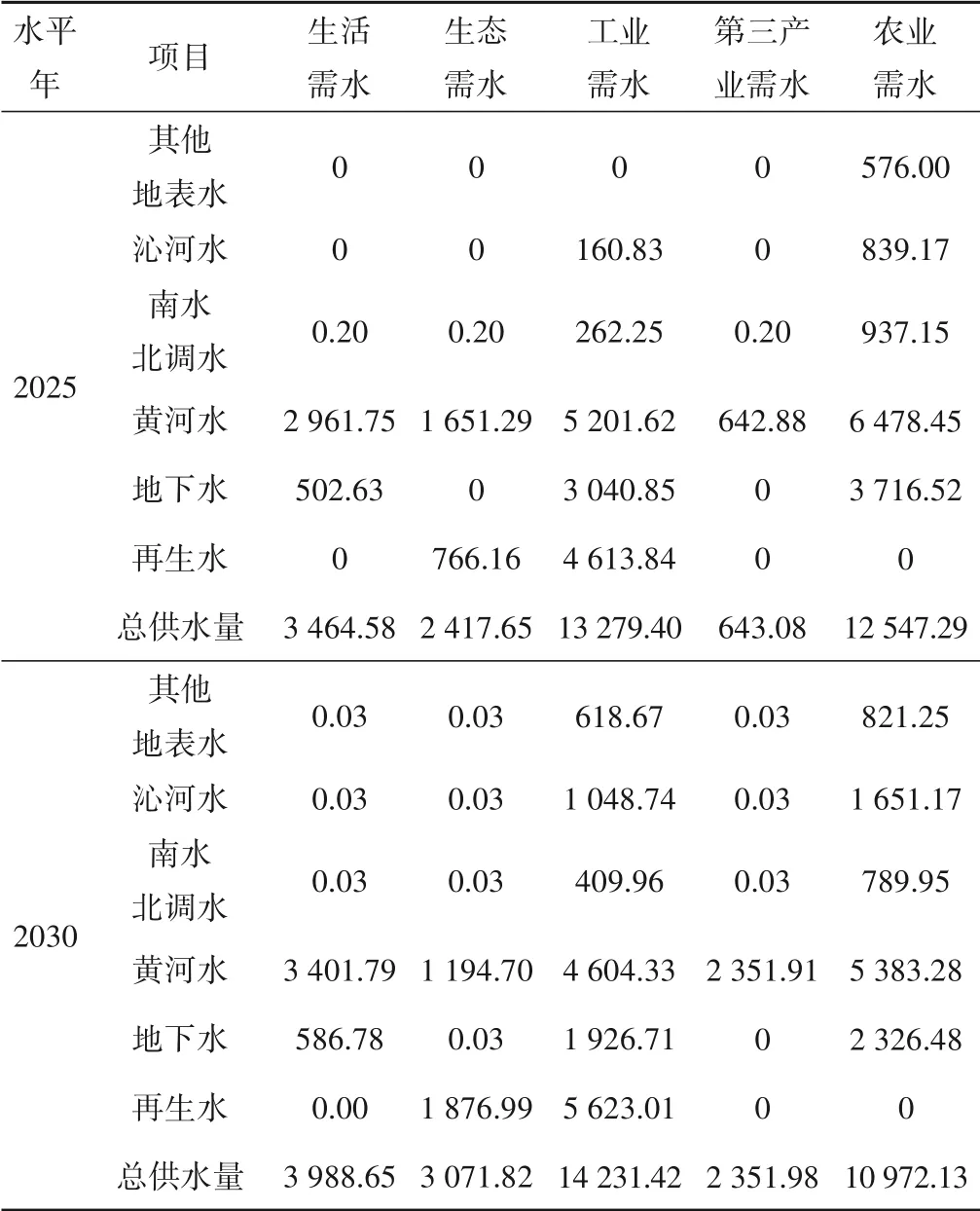
表3 不同水平年的水資源優(yōu)化配置結(jié)果 萬(wàn)m3Tab.3 Results of water resources optimization in different level years
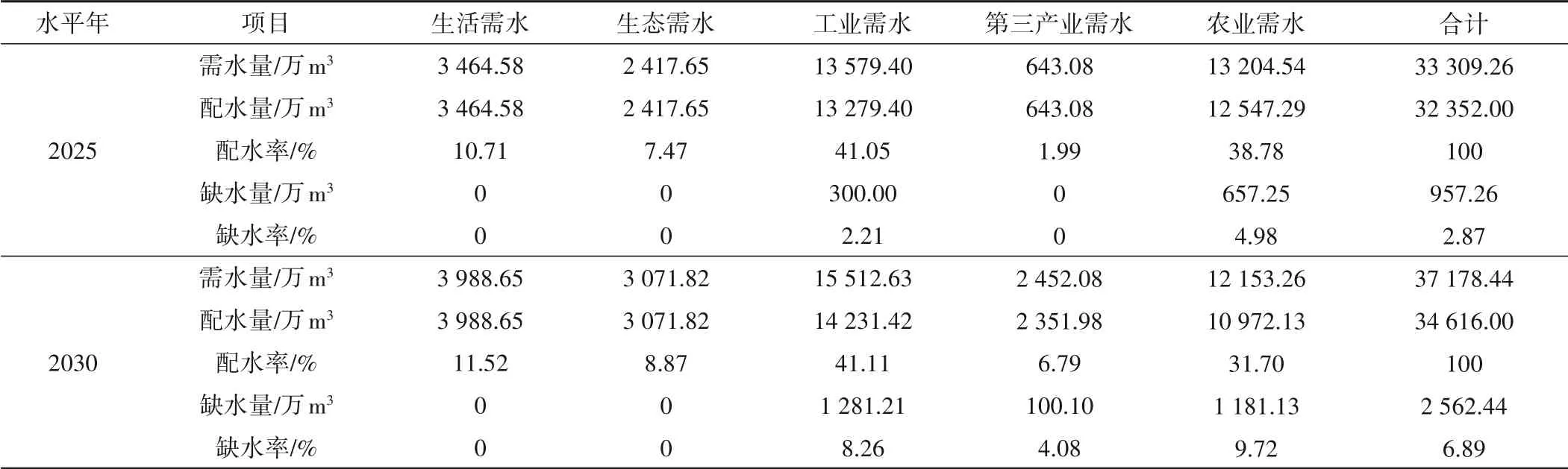
表4 不同水平年的供需平衡關(guān)系表Tab.4 Balance of supply and demand in different level years
(2)缺水量分析。將某縣水資源優(yōu)化配置結(jié)果和需水量預(yù)測(cè)結(jié)果進(jìn)行對(duì)比,可知該配置方案充分滿足生活需水、生態(tài)需水,允許生產(chǎn)部門少量缺水,符合可持續(xù)發(fā)展原則與用戶用水公平原則。該地區(qū)的缺水情況主要集中于生產(chǎn)部門,在生產(chǎn)用水部門配水中,綜合考慮經(jīng)濟(jì)、社會(huì)和生態(tài)效益,盡量保證工業(yè)與第三產(chǎn)業(yè)生產(chǎn)用水的基本需求,允許少量缺水,但由于農(nóng)業(yè)部門用水公平系數(shù)較低,相較于其他兩個(gè)生產(chǎn)部門出現(xiàn)缺水情況較為嚴(yán)重。總體來(lái)看,在經(jīng)濟(jì)、社會(huì)和生態(tài)環(huán)境綜合效益最大的前提下,該區(qū)域不同水平年的缺水率都控制在10%以內(nèi),表明建立的水資源優(yōu)化配置模型和設(shè)置的參數(shù)是合理的。
4 結(jié) 語(yǔ)
本文以經(jīng)濟(jì)、社會(huì)和生態(tài)環(huán)境目標(biāo)函數(shù)及相應(yīng)的約束條件建立河南省某縣的水資源優(yōu)化配置模型,并運(yùn)用鯨魚優(yōu)化算法對(duì)模型進(jìn)行了求解。研究結(jié)果表明2025年和2030年該縣的水資源量可充分滿足生活需水和生態(tài)需水,只在生產(chǎn)用水部門存在少量缺水,缺水率在10%以內(nèi),基本滿足未來(lái)用水需求,配置方案科學(xué)合理,可為該縣未來(lái)的水資源規(guī)劃和管理提供科學(xué)合理的依據(jù)。運(yùn)用的鯨魚優(yōu)化算法克服了傳統(tǒng)優(yōu)化算法收斂速度慢等問(wèn)題,在求解水資源優(yōu)化配置問(wèn)題上表現(xiàn)出較好的適應(yīng)性和有效性,在水資源優(yōu)化配置方面具有良好的應(yīng)用前景。

