級間導葉數對水輪機模式液力透平性能的影響

李延頻，蔣雨煊，張自超，陳金保，陳德新

（1.華北水利水電大學電力學院，鄭州450000；2.武漢大學動力與機械學院，武漢430072）

0 引 言

液力透平作為一種能量回收裝置，廣泛用于工業、電力、農業等領域，通過將來流的動能轉化成機械能，從而實現對液體能量的回收。現階段，液力透平的結構形式主要包水輪機模式，反轉泵模式和專用液力透平。針對不同能量等級的回收，液力透平又有單級和多級液力透平之分，提高液力透平性能對提高能源利用率有現實意義［1］。

對于液力透平，導葉是關鍵的過流部件，關于導葉的研究，楊軍虎［5］采用CFD 軟件對首級導葉數為7，9，11 的3 種液力透平進行數值模擬，發現效率隨導葉片數增多而提高，且較無導葉時透平最高效率點的流量增加、壓頭降低，導葉數為11 時其變化幅度值最小。YABIN T［6］從理論上分析了影響多級能量回收水輪機性能的主要因素，發現轉輪導葉出口段邊緣圓弧半徑是影響水輪機水力效率的決定性因素。紀運廣［7］在液力透平轉輪進口處添加導葉減少了水力損失從而使得效率得到提高，同時基于CFD 軟件對不同導葉開度下的液力透平內部流場進行了分析。史廣泰［8］研究了首級導葉數對液力透平機組工作穩定性的影響，發現首級導葉數增加，葉輪內部的最大脈動幅值減小，對尾水管的脈動幅值影響較小。Timoshevskiy M［9］對高壓水輪機導葉縮尺模型的二維水翼繞流紊流結構的試驗研究結果進行了分析研究。通過上述研究可以發現，導葉對透平的性能影響顯著，但這些研究都僅針對于單級液力透平，而對于多級液力透平而言，級間導葉的損失也占很大一部分［10］。王亞猛［11］對多級水輪機模式液力透平同徑正反導葉進行研究，發現優化級間導葉后對整個液力透平水力效率得到了提高。

現階段，大多數對于液力透平導葉的研究僅針對于首級導葉，對多級液力透平級間導葉的研究較少。為研究級間導葉對多級水輪機模式液力透平的性能影響，本文以一臺二級水輪機模式液力透平為研究對象，選取導葉數不同的五種新型空間導葉，分析導葉數對水輪機模式液力透平的水力特性和壓力脈動影響，為多級水輪機模式液力透平級間導葉的優化提供參考。

1 液力透平的主要參數

本文選取一種以超低比轉速混流式轉輪為的二級液力透平進行研究，其中兩級轉輪結構相同，進水室采用蝸殼進水室，首級導葉選取徑向導葉，級間導葉采用新型空間導葉，具體如圖1 所示；出水室采用環形出水室；部件的基本參數如表1 所示，液力透平結構具體如圖2所示。

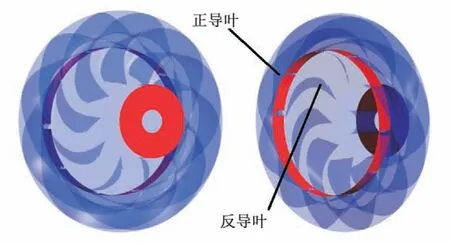
圖1 新型空間導葉結構圖Fig.1 Structure of new space guide vane

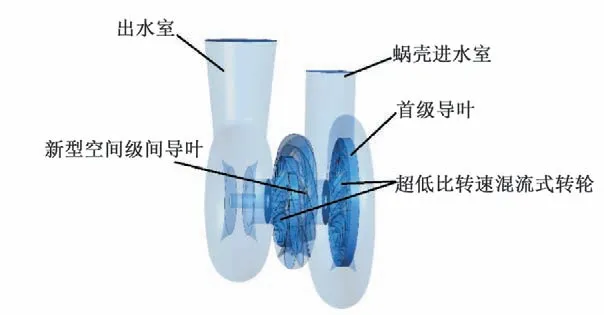
圖2 T模式液力透平Fig.2 T-type hydraulic turbine

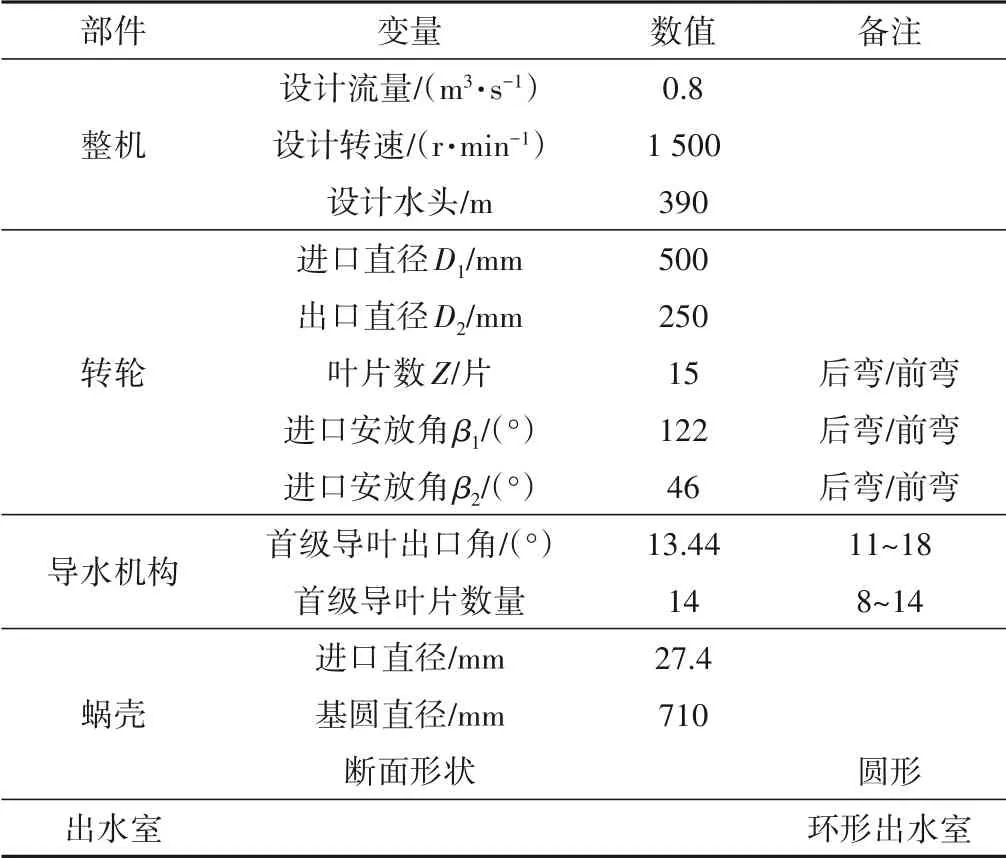
表1 各部件設計參數Tab.1 Design parameters of various components

2 定常計算

2.1 網格劃分與數值模擬計算

基于ICEM，采用非結構化網格中八叉樹的方法對液力透平三維模型進行網格劃分。同時，保證網格質量在0.3 以上，對模型進行網格無關性驗證，當網格數在550 萬個左右時，效率和水頭浮動均在0.5%以內，具體如圖3所示。

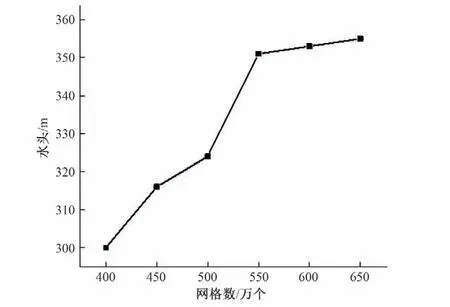
圖3 計算域網格劃分無關性驗證Fig.3 Verification of grid independence in computational domain

數值模擬方面，運用CFD-fluent 軟件對模型進行全流道定常計算，數值計算求解方法采用有限體積法，假設為不可壓縮三維流動，且滿足連續性方程和動量方程，選用標準k-ε湍流模型，收斂精度設為10-4。液力透平進口邊界設置為速度進口，出口設置為無壓力出口，所有壁面的邊界條件選擇為wall，設置為固定壁面，滿足無滑移條件，各部件交界面設置為interface。

2.2 實驗驗證

為了驗證數值計算的準確性，對采用新型空間導葉數為10的模型進行性能實驗，具體試驗示意圖如圖4 所示。實驗結果如圖5 顯示，可以看出，試驗和數值模擬得到性能曲線趨勢一致，由于數值模擬沒有考慮機械損失，還忽略了平衡孔泄露損失，所以計算結果偏大。在最高效率點，采用相對誤差值計算，水頭誤差為3.1%，效率誤差為6.57%，可見本文所采用的數值計算方法能較好的預測透平性能。

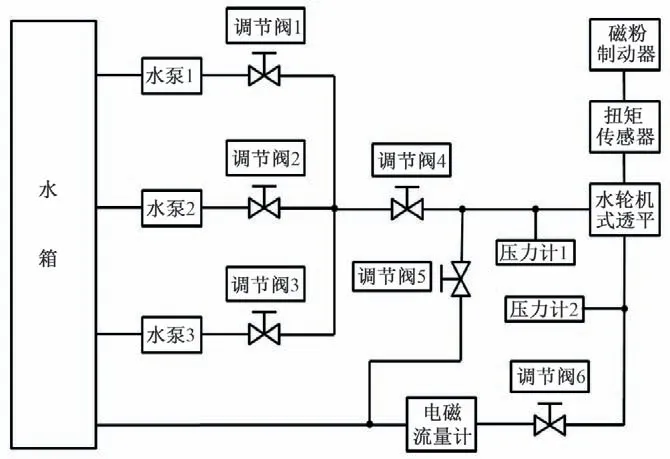
圖4 液力透平試驗臺Fig.4 Hydraulic turbine test bench

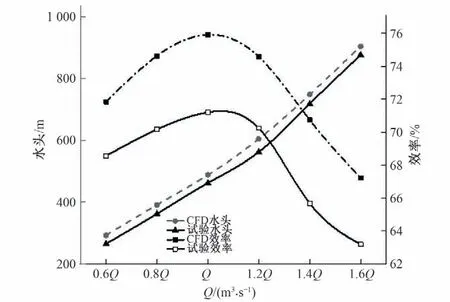
圖5 效率最優的模型透平試驗外特性和數值模擬外特性對比Fig.5 Comparison of external characteristics of model turbine test and numerical simulation with optimal efficiency

2.3 流量-效率、流量-可利用水頭外特性分析

選取導葉數分別6、8、10、12、13 的新型空間導葉，通過CFD-fluent 計算得到在0.6Q、0.8Q、Q、1.2Q、1.4Q、1.6Q工況下，得到整個T 模式液力透平的效率和可利用水頭變化如圖6所示。

如圖6所示，隨著導葉數的增加，液力透平效率先增大后減小，在導葉數為12 時，效率最高。同時，5 種不同導葉數下，液力透平均在額定工況處達到效率最高。轉輪和新型空間導葉損失計算結果如圖7顯示，新型空間導葉數增加，轉輪的水頭損失下降。因此分析原因為隨著導葉數增加，導葉對水流的導控能力增強，導葉間水流流態變好，導葉和轉輪的損失都逐漸減小，但當數量達到一定數時，導葉的摩擦損失增加，損失開始增大，效率有所降低。同時導葉數增加，總可利用水頭均呈現增加趨勢，原因為導葉數增加，導葉摩擦損失和整個裝置的總可利用水頭也逐漸增加。

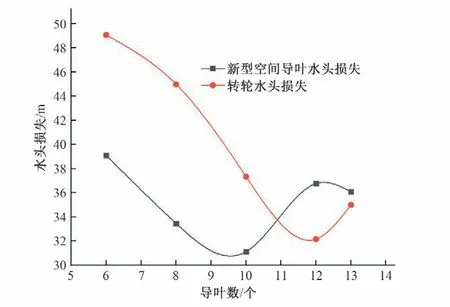
圖7 新型空間導葉和轉輪水頭損失Fig.7 Head loss of new space guide vane and runner

2.4 內部流態

外特性中可利用水頭和效率的變化是由內部流態的變化引起的，導葉數變化會引起導葉內靜態壓力，流線等內部能量特性發生變化，靜態壓力越大，對應的能量損失以越大，內部流態穩定性就越小；流線直接反映出液流在流道中的流態好壞。

2.4.1 新型空間導葉內部靜壓力特性分析

對于五種方案進行定常計算，得到壓力云圖如圖8 所示。隨著導葉數的增加，壓力逐步上升，反導葉高壓區范圍擴大，從導葉數為10 開始，高壓區延伸到過渡段和正導葉處，隨后呈梯度減小，在正導葉出口處壓力降到最低。但對所接轉輪的內部壓力分布幾乎沒有影響，分析原因可能為導葉數增加，導葉導控能力增加，液體所流流道面積減小，流速增加，壓力上升，這與導葉數增加可利用水頭增加的規律相符。

圖8 不同導葉數壓力云圖Fig.8 Pressure nephogram with different number of guide vanes

2.4.2 流線分布

對于5 種方案進行定常計算，得到不同導葉數內部流線圖如圖9 所示。導葉數增加，對新型空間導葉內部流態沒有顯著影響，除導葉數為12 和13 時反導葉處出現少量漩渦，其余無明顯區別，但對所接轉輪中內部流態影響顯著。導葉數增加，所接轉輪內部流線逐漸變好，導葉數最高13 時，轉輪進口幾乎沒有渦流，原因為導葉數增加，控制液流能力增強，使之更能夠以符合轉輪所需液流方向進入下級轉輪。

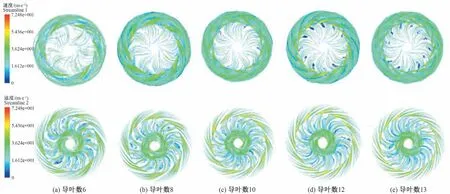
圖9 不同導葉數內部流線分布Fig.9 Internal streamline distribution with different number of guide vanes

3 壓力脈動分析

3.1 監測點布置及計算設置

透平內部的壓力脈動是造成裝置振動的主要因素之一，而透平內部的壓力脈動主要是由過流部件之間的動靜干涉產生的。數值結果顯示，轉輪和級間導葉的損失占到整體損失的50%以上，為了研究不同級間導葉數對透平內部壓力脈動的影響，本文選取兩級轉輪和新型空間導葉作為脈動研究對象，分別在首級轉輪，二級轉輪和新型空間導級間導葉內布置壓力監測點，并在額定流量工況下進行非定常計算，具體壓力監測點的布置方式如圖10所示。

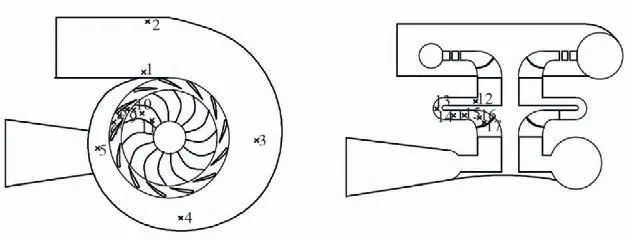
圖10 監測點的選取Fig.10 Selection of monitoring points

為了消除靜壓對結果的干擾，引入壓力系數Cp對壓力脈動結果進行分析。Cp表達式如下：

式中：P為瞬時壓力為采用時間內的平均壓力；ρ為液體密度；U為葉輪出口圓周速度。

3.2 轉輪內壓力脈動分析

3.2.1 一級轉輪內部壓力脈動

通過數值計算得到不同級間導葉數下一級轉輪內部壓力脈動頻域圖和最大脈動壓力值表如圖11 和表2 所示。可以看出，不同導葉數下，沿著流動方向，監測點壓力脈動主頻幅值均呈現減小的趨勢，越靠近轉輪出口，幅值越小，這是因為在進口接近耦合面，動靜干涉較為強烈，越遠離進口所受動靜干涉越小。同時，隨著導葉數增加，一級轉輪內部進出口壓力脈動變化幅值不明顯，但有增大趨勢，靠近進口處的監測點9和靠近出口處的監測點11 主頻幅值均增加，這是因為級間導葉數增多，反導葉進口處過流面積越小，導葉進口處流道內流速增大，一級轉輪所受的動靜干涉也就越強烈，主頻幅值隨之增加。

圖11 一級轉輪內壓力脈動頻域圖Fig.11 Frequency domain diagram of pressure fluctuation in primary runner

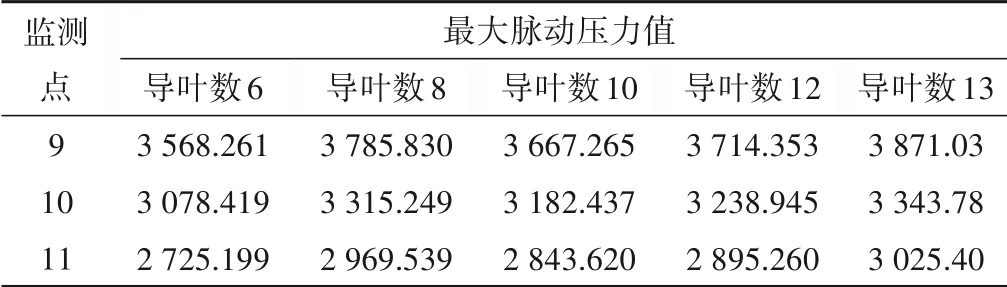
表2 一級轉輪內最大脈動壓力值 kPaTab.2 Maximum pulsating pressure value in the primary runner

3.2.2 二級轉輪內部壓力脈動

通過數值計算得到二級轉輪內部壓力脈動頻域圖和最大脈動壓力值表如圖12 和表3 所示。可以看出，不同新型空間導葉數下，沿流動方向，壓力脈動主頻幅值和最大脈動幅值均呈現減小趨勢。原因為二級轉輪進口處與級間導葉連接，級間導葉和轉輪動靜干涉，產生的壓力脈動幅值變大，距離進口越遠，受干涉強度越小，壓力脈動幅值也就越小。還可以看出，隨著新型空間導葉數的增加，轉輪進口處的脈動幅值總體為減小趨勢，說明級間導葉數增加，正導葉內流道減小，級間導葉內對束流能力增強，對應圖9 可以看出，隨著級間導葉數增加，二級轉輪進口的液力流態變好，從而轉輪進口處脈動幅值減小；同時，二級轉輪出口的主頻幅值和最大脈動幅值變化不明顯，級間導葉數對二級轉輪的影響主要體現在轉輪進口處，可見，適當增加導葉數可以減小二級轉輪進口處壓力脈動幅值。

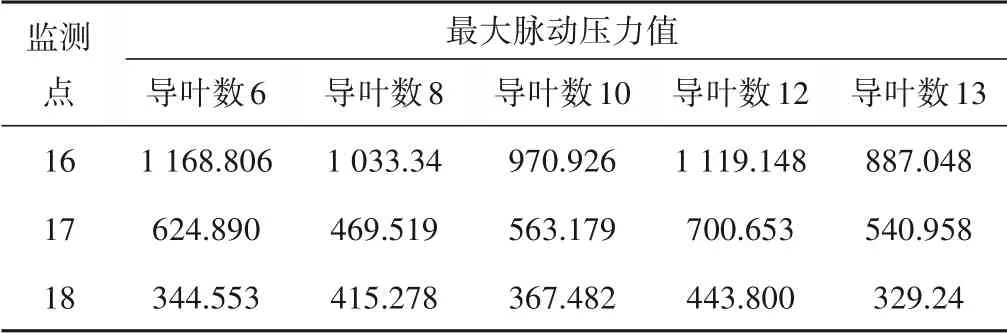
表3 二級轉輪內最大脈動壓力值 kPaTab.3 Maximum pulsating pressure value in the secondary runner

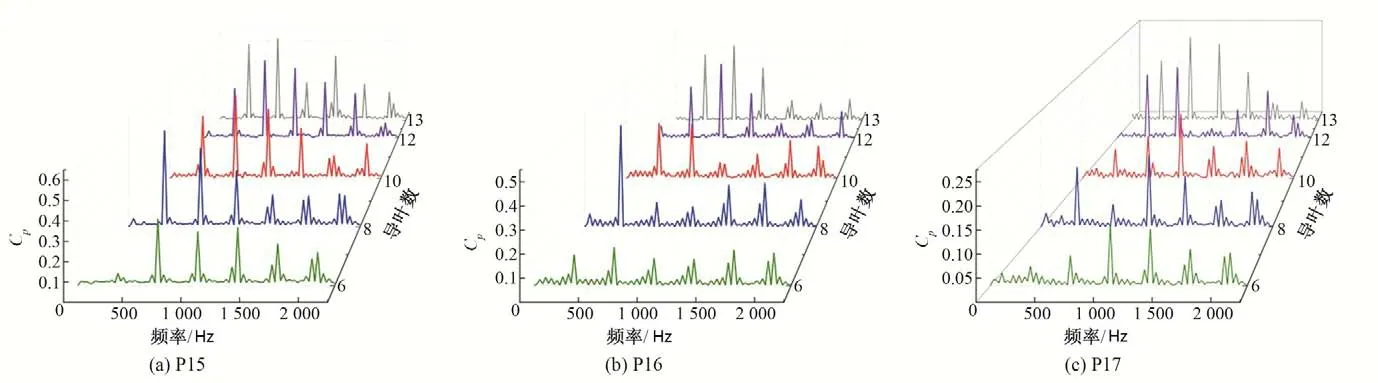
圖12 二級轉輪內壓力脈動頻域圖Fig.12 Frequency domain diagram of pressure fluctuation in secondary runner

同時，對比一級轉輪內部脈動幅值變化，級間導葉數增加，對二級轉輪內部壓力脈動幅影響更為顯著。

3.3 級間導葉壓力脈動分析

圖13 為將數值計算進行傅里葉變換得到的級間導葉內各檢測點的壓力脈動頻域圖，表4為通過數值計算的方法得到級間導葉內各檢測點處的最大脈動壓力值。

結合圖13 和表4 可以看出，不同級間導葉數下，沿液體流動方向，壓力脈動主頻幅值均逐漸減小，但級間導葉數增加，反導葉進口和正導葉出口處的壓力脈動主頻幅值均增大，因為導葉數增加，流道面積減小，流道內流速和壓力值上升，結合圖8壓力云圖可以看出，正導葉和反導葉處壓力值上升，脈動強度也跟著上升，可以看出，導葉數為8 時，正導葉導葉出口處脈動幅值最小，但是反導葉進口處脈動幅值大，導葉數為10時，反導葉進口處壓力脈動幅值最小，且正導葉出口處僅比導葉數為8時脈動幅值打，可見，在一定參數范圍內，適當增加導葉數能降低導葉內部自身的壓力脈動幅值。

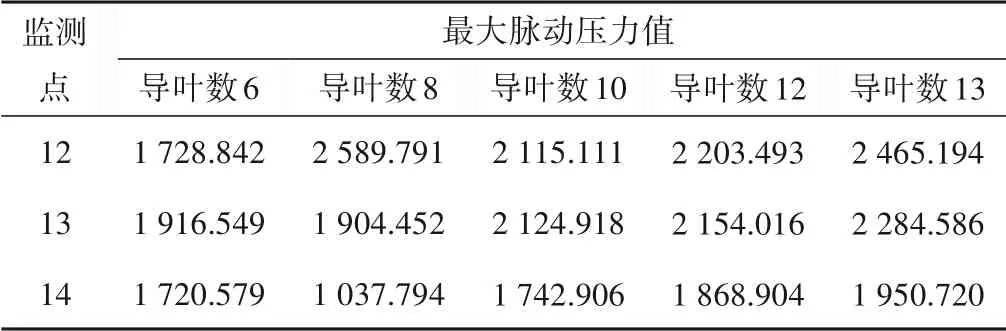
表4 級間導葉內最大脈動壓力值 kPaTab.4 Maximum pulsating pressure value in the interstage guide vane

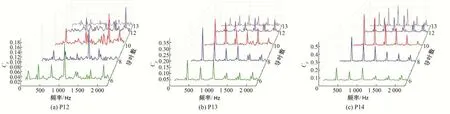
圖13 級間導葉內壓力脈動頻域圖Fig.13 Frequency domain diagram of pressure fluctuation in interstage guide vane

4 結 論

（1）新型空間級間導葉數增加，整個T模式液力透平效率先增加后減小，最高效率出現在導葉數為12 時；可利用水頭為逐漸增加的趨勢；不同流量工況下，導葉數增加，效率也為先增大后減小，可利用水頭逐漸增加，五種模型的最優效率和可利用水頭均出現在額定工況附近。

（2）新型空間導葉數增加，導葉內部靜態壓力值，流線均發生變化。導葉數增多，正導葉處逐漸出現高壓區，反導葉處高壓區面積增大；同時，級間導葉數增加所接轉輪進口流線變優，但是反導葉處出現漩渦，當導葉數為12 時，靜壓和流態處于較優狀態。

（3）新型空間導葉數增加，一級轉輪內部脈動幅值增加、二級轉輪內部壓力脈動主頻幅值減小，新型空間導葉自身內部壓力脈動幅值增加。但是一級轉輪和導葉內部脈動幅值增加幅度小于二級轉輪內部脈動減小幅值，因此，在一定透平結構參數下，適當的增加新型空間導葉數能減小透平內部壓力脈動幅值。

（4）綜合上述研究可知，級間導葉數對水輪機式多級液力透平水力性能和壓力脈動特性影響較大，綜合其水力特性和壓力脈動特性，對于本文中的液力透平，推薦最佳級間導葉數為12。