月牙肋岔管有限元結構計算基本原則與方法

申 艷，黃永松，馮浩文

（華北電力大學可再生能源學院，北京102206）

1 問題的提出

由于具有受力明確合理、設計方便、水流流態好、水頭損失小、結構可靠、制作安裝容易等特點，在國內外大中型常規和抽水蓄能電站地下埋管中，月牙肋岔管被廣泛應用。但由于埋藏式月牙肋岔管體形及作用機理復雜，用傳統的解析方法難以得到理想的計算結果。有限單元法是隨著電子計算機的發展而迅速發展起來的一種現代計算方法，它能夠模擬復雜的體形和邊界條件，且計算精度可靠，是一種有效的結構數值分析手段。有限單元法在方案優化、敏感性分析、計算精度以及研究成本等方面較其他的分析方法有明顯的優勢。因此，鋼岔管設計宜采用三維有限元法進行結構分析。

岔管有限元結構分析的專業性較強，對分析人員的力學基礎、研究對象的作用機理和程序熟練程度有較高的要求。在分析過程中，單元類型的選擇、網格密度的選取、模型范圍的選取、悶頭及支撐的模擬方式、邊界約束條件等因素對計算結果和分析結論都有一定的影響。因此，有必要對上述各種因素進行系統地分析與評估，提出一套適合埋藏式月牙肋岔管有限元結構計算的基本規定。

2 月牙肋鋼岔管有限元結構計算的基本規定

2.1 單元類型的選擇

在進行單元類型對有限元計算成果影響分析時，根據月牙岔管的受力特點，對管殼和肋板采用不同單元型式進行研究。月牙肋岔管是一個復雜的空間三維結構，通常可以采用殼單元或實體單元進行模擬。其中殼單元可簡化模擬厚度方向尺度遠小于整體結構尺寸的模型，一般認為某一方向尺度（厚度方向）小于整體結構尺寸的1/10，且沿厚度方向的應力可忽略的特征的結構。月牙肋岔管的肋板是岔管的加強構件，通常可以采用殼單元或實體單元進行模擬。由于肋板厚度較厚，且在進行肋板應力分析時，肋板厚度方向的應力也需要被關注，故通常在進行有限元結構分析時采用精度較高的八節點實體單元來模擬肋板。

2.1.1 管殼單元

為研究管殼單元類型對計算結果的影響，以圓管段為例分別采用殼單元和實體單元模擬進行有限元結構計算，埋管狀態采用點點接觸模擬圍巖的作用，將結果與解析解進行對比分析。分析表明：當采用4 節點殼單元或8 節點實體單元模擬管殼，采用點點接觸單元模擬圍巖的作用，單元網格尺寸與主管半徑的比值為0.1 時，兩種類型的單元均能較好地反應鋼管在明管狀態和埋管狀態下的應力狀態，計算成果基本相同，且與理論計算結果也基本一致，管殼采用殼單元和實體單元的計算精度均能滿足工程要求。

2.1.2 肋板單元

為研究肋板單元類型對計算結果的影響，以豐寧抽水蓄能電站鋼岔管為例，保持鋼岔管體形及管殼有限元網格不變，肋板按實體單元和殼單元分別建立有限元模型并進行結構計算。分析表明：

肋板的單元類型對管殼和肋板的應力都有一定的影響。無論明管狀態還是埋管狀態，單元類型對靠近肋板的管殼影響較大。殼單元與實體單元相比，局部膜應力相對差別均在8%以內，而局部膜應力+彎曲應力則差別較大，差值一般在±（10%～50%）范圍，明管狀態最大差別可達79%，埋管狀態下最大也達69%。對遠離肋板的管殼的影響較小，無論是局部膜應力還是彎曲應力，殼單元與實體單元相比差別均較小，相對差別一般不足3%。造成以上結果的原因，主要是兩種單元在模擬肋板平面內的剛度時有較大差別所致。

肋板的單元類型對肋板的應力影響程度與管殼相比要大些。明管狀態下在兩種類型單元的計算結果最大差別為5.4%，出現在部位為肋板腰部斷面內側；埋管狀態下，兩種類型單元的計算結果最大差別為6.8%，出現部位為肋板腰部斷面外側。

由于肋板沿板厚方向承受拉應力，因此肋板Z向應力也是值得關注的。然而，采用殼單元無法模擬肋板厚度方向受力特點，難以較全面反應肋板的應力狀態，而實體單元能較好的模擬肋板的應力狀態，因此建議肋板采用實體單元模擬。

2.1.3 網格密度

有限元分析結果的精度與離散模型的網格密度密切相關。模型網格過稀，會對計算精度甚至計算結果產生不利影響，模型網格過密，又會導致有限元模型的規模過大，影響有限元分析的效率。如何在保證計算精度的前提下，劃分合理密度的有限元網格，提高計算效率，是需要關注的問題。為說明不同網格密度對月牙肋鋼岔管有限元結構計算精度的影響，分別選擇對稱“Y”形鋼岔管和非對稱“Y”形鋼岔管進行分析，對稱“Y”形鋼岔管以豐寧鋼岔管為例，非對稱“Y”形鋼岔管以引子渡2 號鋼岔管為例。為研究網格密度對計算結果的影響，對同樣的鋼岔管模型，單元尺寸（C）與公切球半徑（R）的比值分別取0.26、0.2、0.13、0.1、0.07 進行計算分析，關鍵點的位置示意見圖1，關鍵點Mises 應力相對誤差與網格密度的關系曲線見圖2～圖9。通過圓管段的有限元計算結果與解析解計算結果進行對比可知：采用殼單元簡化模擬管殼，采用點點接觸單元模擬圍巖的作用，當C/R=0.1 時，能夠較好地反應鋼管明管狀態和埋管狀態下的受力情況，有限元的計算結果與解析解十分接近，明管的計算誤差不超過0.3%，埋管的計算誤差不超過1.3%。由于岔管應力計算沒有解析解，本文假定認為網格密度最大的C/R=0.07 方案的計算結果最接近于理論解，應力相對誤差是其他方案的應力值相對于網格密度最大的C/R=0.07 方案的應力值而言的。

圖1 關鍵點位置示意圖Fig.1 Schematic diagram of the locations of key points

圖2 關鍵點中面Mises應力相對誤差與網格密度的關系曲線（對稱鋼岔管明管狀態）Fig.2 Relationship between mean surface Mises stress relative error and grid density at Key points（Open pipe state of symmetric Bifurcation pipe）

圖3 肋板關鍵點Mises應力相對誤差與網格密度的關系曲線（對稱鋼岔管明管狀態）Fig.3 Relationship between Mises stress relative Error of Key floor points and Grid Density（With symmetric Bifurcation pipe open pipe state）

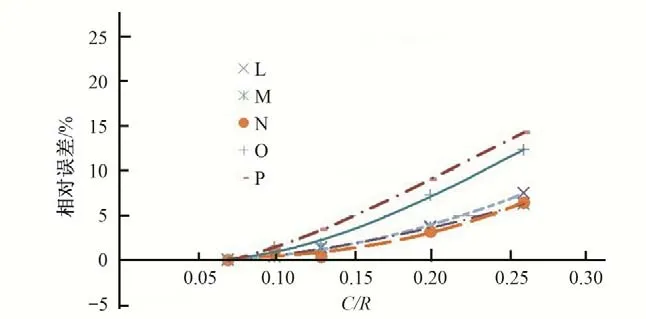
圖4 關鍵點中面Mises應力相對誤差與網格密度的關系曲線（對稱鋼岔管埋管狀態）Fig.4 Relationship between mean surface Mises stress relative error and grid density at Key points（Buried state of symmetric Bifurcated steel tubes）

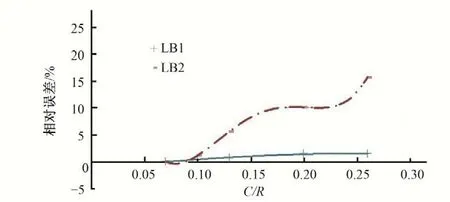
圖5 肋板關鍵點Mises應力相對誤差與網格密度的關系曲線（對稱鋼岔管埋管狀態）Fig.5 Relationship between Mises stress relative Error of Key floor points and Grid Density（Buried state of symmetric Bifurcated steel tubes）

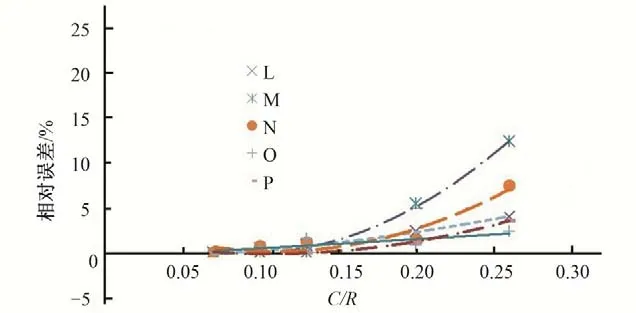
圖6 關鍵點中面Mises應力相對誤差與網格密度的關系曲線（卜形鋼岔管明管狀態）Fig.6 Relationship between mean surface Mises stress relative error and grid density at Key points（Asymmetric Y bifurcation pipe state）

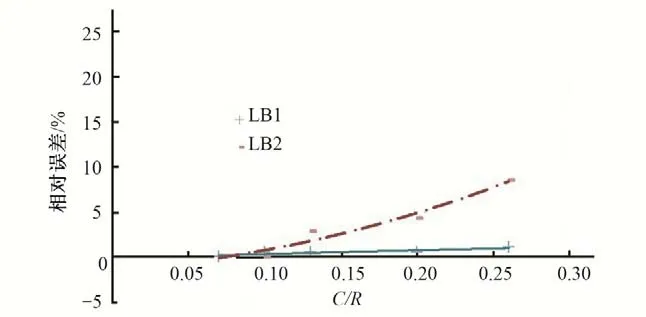
圖7 肋板關鍵點Mises應力相對誤差與網格密度的關系曲線（卜形鋼岔管明管狀態）Fig.7 Relationship between the Mises stress relative error of key floor points and grid density（Asymmetrical Y bifurcation pipe open pipe state）

圖8 關鍵點中面Mises應力相對誤差與網格密度的關系曲線（卜形鋼岔管埋管狀態）Fig.8 Relationship between mean surface Mises stress relative error and grid density at Key points（Asymmetric Y bifurcation pipe state）

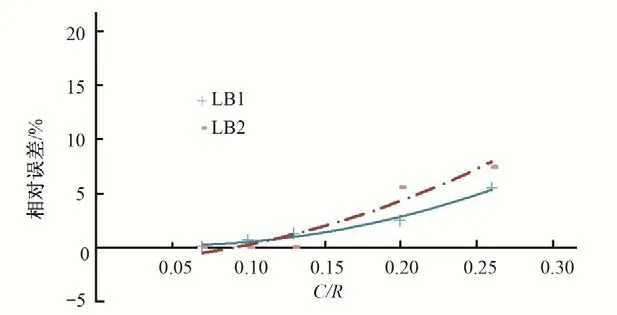
圖9 肋板關鍵點Mises應力相對誤差與網格密度的關系曲線（卜形鋼岔管埋管狀態）Fig.9 Relationship between the Mises stress relative error of key floor points and grid density（Asymmetrical Y bifurcation pipe open pipe state）

計算成果表明：對于鋼岔管有限元計算而言，單元尺寸越小，結果會越精確，計算的相對誤差越小。隨著單元尺寸的縮小，應力值的相對誤差下降很快，但當單元尺寸C/R小于0.1后，隨著單元尺寸縮小，應力值的誤差降低變得緩慢。無論是明管狀態還是埋管狀態，當C/R小于0.1時，計算誤差相對較小，一般不超過2%，在有限元結構計算時，建議網格密度參數C/R的比值在0.08～0.10之間選取，既能保證計算精度，又不至于模型的規模太大而影響計算分析效率。

2.2 模型范圍

為研究模型范圍對計算結果的影響，分別以豐寧抽水蓄能電站對稱“Y”形鋼岔管，和引子渡2號鋼岔管非對稱Y形鋼岔管為例進行說明。對同樣的鋼岔管模型，支管的長度（L）與主、支管半徑（R）的比值分別取1.0、2.0、3.0、4.0、6.0 進行計算分析，關鍵點的位置示意見圖1，關鍵點Mises應力與模型范圍的關系曲線見圖10～圖17。計算結果表明：模型范圍參數L/R從1～6之間變化時，明管狀態下，對稱鋼岔管肋板及腰線折角M、L 點的應力對模型范圍較為敏感；非對稱Y形鋼岔管支管轉折點J、M、N、O 的應力對模型范圍較為敏感。埋管狀態下，受圍巖的約束，特征點的Mises 應力變化較小，表明埋管狀態下的計算結果對模型范圍不敏感。

圖10 關鍵點中面Mises應力與模型范圍的關系曲線（豐寧鋼岔管明管狀態）Fig.10 Relationship between Mises stress on the midface of key points and model range（Open pipe condition of Fengning steel bifurcation pipe）

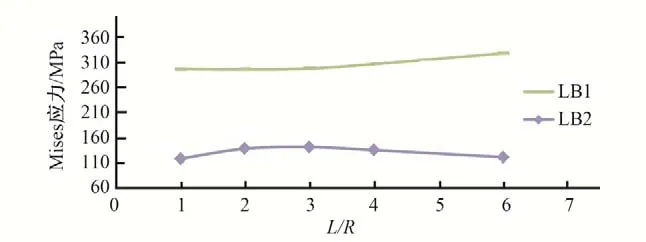
圖11 肋板關鍵點Mises應力與模型范圍的關系曲線（豐寧鋼岔管明管狀態）Fig.11 Relationship between Mises stress on key floor points and model range（Open pipe condition of Fengning steel bifurcation pipe）

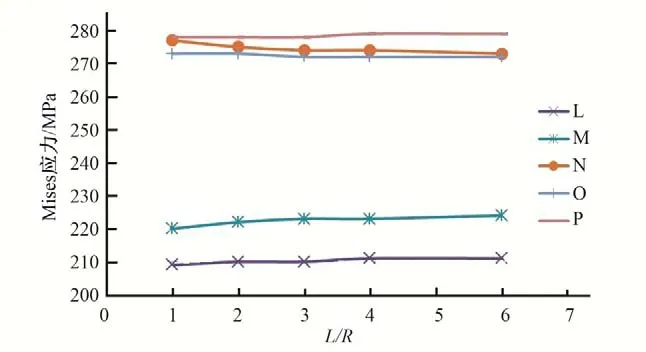
圖12 關鍵點中面Mises應力與模型范圍的關系曲線（豐寧鋼岔管埋管狀態）Fig.12 Relationship between Mises stress on the midface of key points and model range（Buried state of Fengning steel bifurcation pipe）

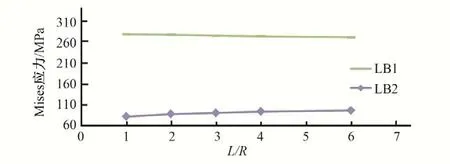
圖13 肋板關鍵點Mises應力與模型范圍的關系曲線（豐寧鋼岔管埋管狀態）Fig.13 Relationship between Mises stress on key floor points and model range（Buried state of Fengning steel bifurcation pipe）

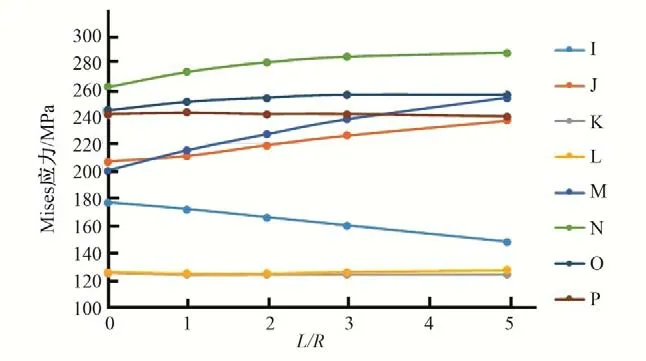
圖14 關鍵點中面Mises應力與模型范圍的關系曲線（引子渡2號鋼岔管明管狀態）Fig.14 Relationship between Mises stress on the midface of key points and model range（Open pipe condition of Yinzidu No.2 steel bifurcation pipe）

圖15 肋板關鍵點Mises應力與模型范圍的關系曲線（引子渡2號鋼岔管明管狀態）Fig.15 Relationship between Mises stress on key floor points and model range（Open pipe condition of Yinzidu No.2 steel bifurcation pipe）

圖16 關鍵點中面Mises應力與模型范圍的關系曲線（引子渡2號鋼岔管埋管狀態）Fig.16 Relationship between Mises stress on the midface of key points and model range（Buried state of Yinzidu No.2 steel bifurcation pipe）

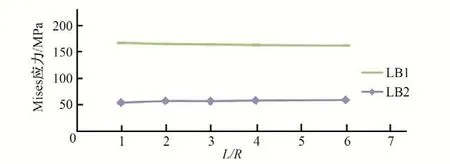
圖17 肋板關鍵點Mises應力與模型范圍的關系曲線（引子渡2號鋼岔管埋管狀態）Fig.17 Relationship between Mises stress on key floor points and model range（（Buried state of Yinzidu No.2 steel bifurcation pipe）

計算范圍對計算成果影響主要體現在兩方面，一是計算邊界約束對鋼岔管主體的影響，二是由于鋼岔管體形復雜，在內水壓力作用下，沿鋼岔管軸線會產生不平衡力，如果模型范圍選取過大，會導致計算結果誤差增大。因此，在明管狀態下，鋼岔管計算范圍受上述兩個因素影響，不宜過大，通過計算分析，L/R在3～4 范圍內選取比較合適。對埋管狀態，由于受到圍巖的約束，這種不平衡力對計算成果的影響較小，以計算邊界約束條件的影響為主，因此，在選擇有限元模型范圍時，建議主、支管的長度（L）與主、支管半徑（R）的比值取3～4為宜。當岔管公切球與支管直徑相差較大時，宜對支管長度適當延長。

2.3 水重及結構自重的影響

通過對豐寧岔管水壓試驗工況下是否考慮水重及結構自重的有限元計算結果對比分析可知：

（1）無論是否考慮水重及結構自重，岔管的應力分布規律基本相同。相比較而言，是否考慮水重及結構自重，對肋板應力分布的影響較為明顯。

（2）當試驗壓力采用7.3 MPa 時，水重和結構自重所占比重較小，是否考慮水重及結構自重，特征點的應力相差通常不超過10%；當試驗壓力采用3.7 MPa 時，水重和結構自重所占比重適中，是否考慮水重及結構自重，特征點的應力相差通常不超過20%；當試驗壓力采用1.0 MPa 時，水重和結構自重所占比重較大，是否考慮水重及結構自重，特征點的應力相差甚至超過了30%；水重及結構自重對計算結果的影響程度與水重及結構自重在荷載中所占的比例有關，所占比例小影響就小，所占比例大影響就大。

（3）采用有限元進行岔管水壓試驗工況下的結構計算時，考慮水重和結構自重比較容易實現，建議在有限元計算中按實際情況考慮水重和結構自重。

2.4 悶頭的模擬方式

在進行水壓試驗工況的結構計算時，需要考慮悶頭的作用，通常有兩種模擬方式：①按水壓試驗的實際情況，在有限元網格劃分時考慮悶頭；②采用簡化的邊界條件進行模擬，具體來說：在主管管口施加軸向約束，在兩支管管口施加軸向節點拉力，其節點力的合力與其悶頭上所受壓力相等。簡化的模擬方式相對于模擬悶頭的實際情況的相對誤差一般不超過5%，但在支管過渡錐的相對誤差較大，M 點的相對誤差甚至超過了10%。建議在進行水壓試驗工況的結構計算時，按悶頭的實際情況模擬悶頭的作用。

2.5 支撐的模擬方式

通過對豐寧岔管水壓試驗工況下不考慮支撐和模擬支撐的有限元計算結果對比分析可知：

（1）從上半部分的應力分布規律來看，是否考慮支撐對應力部分影響較小；從下半部分的應力云圖以及支墩處節點的應力可以看出，由于考慮支撐的模型同時考慮了結構自重、水重以及支墩的作用，部分支墩處的節點呈現一定的彎曲作用和應力集中，但總體的應力水平不高。

（2）支撐的模擬對各個特征點應力有一定的影響，當具體到每個特征點，其影響程度有所不同，是否考慮支撐的相對誤差一般不超過5%，但是在支管過渡錐的特征點的相對誤差超過了10%。

（3）由于在內水壓力作用下，肋板處于偏心受彎的受力情況，是否考慮支撐、水重、結構自重對于肋板的應力影響較為明顯；以豐寧為例，在水壓試驗工況下，肋板的應力水平不高，是否考慮支撐對肋板特征點計算相對偏差超過20%。

（4）由于是否考慮支撐對個別部位應力的影響較大，建議在進行水壓試驗工況結構計算時，建議盡量按照實際情況模擬支撐的作用。

2.6 約束條件

通過對豐寧岔管運行工況下，不同約束條件下的有限元計算結果對比分析可知：

（1）無論是在明管狀態還是埋管狀態，全約束和平動3自由度約束的計算結果幾乎一致，可見是否約束岔管端部邊界的旋轉自由度對計算結果影響可以忽略。

（2）在明管狀態下，對比平動3自由度約束以及法向約束的計算結果可知，如果只是約束法向的自由度而不約束平面內的自由度，特征點的計算結果相差一般在5%以內，也有個別特征點如肋板、肋旁管壁，支管轉折點等部位相差超過了10%，邊界約束條件的影響不可以忽略。

（3）在埋管狀態下，對比全約束、平動3自由度、法向約束等3 種不同約束條件下的計算結果可知：由于圍巖的約束作用較強，岔管端部的約束條件對岔管的計算結果影響很小，一般不超過1%。

（4）基于以上幾點，并考慮到明管狀態的分析需要，建議在進行岔管有限元結構計算時，模型端部的約束條件選取全約束或平動3自由度約束。

3 結 論

（1）在月牙肋岔管有限元結構計算中，為保證計算精度單元建議按照以下原則進行選擇：肋板選擇8節點實體單元模擬；管殼選擇4節點殼單元模擬；埋管狀態下，鋼襯與圍巖的聯合承載選擇點點接觸單元進行模擬。

（2）對于岔管有限元計算而言，單元尺寸越小，結果會越精確，計算的相對誤差越小。隨著單元尺寸的縮小，應力值的相對誤差下降很快，但當單元尺寸縮小到一定程度后，應力值的相對誤差下降變成緩慢。無論是明管狀態還是埋管狀態，當單元尺寸與公切球半徑的比值建議在0.08～0.10之間選擇，計算相對誤差相對較小，可以滿足工程計算精度的要求，也不至于使網格過密而影響計算分析效率。

（3）在選擇有限元模型范圍時，為了減小約束端的局部應力影響，主、支管的長度（L）與主、支管半徑（R）的比值建議在3～4 范圍選擇。當公切球與支管直徑相差較大時，宜對支管長度適當延長。

（4）水重及結構自重在荷載中所占的比例大小決定水重及結構自重對計算結果的影響程度；采用有限元進行岔管水壓試驗工況下的結構計算時，考慮水重和結構自重比較容易實現，建議在有限元計算中按實際情況考慮。

（5）通過對實際悶頭和簡化模擬兩種方式的對比分析可知，簡化的模擬方式相對于模擬悶頭的實際情況的相對誤差一般不超過5%，但是在支管過渡錐的相對誤差較大，M 點的相對誤差甚至超過了10%。因此，在進行水壓試驗工況的有限元結構計算時，建議按照水壓試驗的實際情況，在有限元網格劃分時考慮悶頭。

（6）通過對豐寧岔管水壓試驗工況下不考慮支撐和模擬支撐的有限元計算結果對比分析可知，是否考慮支撐的相對誤差一般不超過5%，但是在支管過渡錐的特征點以及肋板特征點，計算相對誤差較大；另外，在支撐部位也會引起局部的彎曲應力和應力集中。因此，在進行水壓試驗工況的有限元結構計算時，建議按照支撐的實際情況，在有限元結構計算中予以考慮。

（7）約束條件不同對明管狀態下的影響要大于埋管狀態，考慮到明管狀態的分析需要，建議在進行岔管有限元結構計算時，模型端部的約束條件選取全約束或平動3自由度約束。