預應力錨索的張拉次序對閘墩應力及變形的影響研究

王己海，費文平

（1.四川大學水力學與山區(qū)河流開發(fā)保護國家重點實驗室，成都610065；2.四川大學水利水電學院，成都610065）

0 引 言

預應力閘墩是保證大型泄水建筑物安全的重要結構，這種采用預應力錨索與閘墩結合的技術能夠有效改善閘墩的應力狀態(tài)，確保在弧門推力的作用下閘墩結構的安全可靠。在預應力錨索與水推力的共同作用下，閘墩結構的應力與變形狀態(tài)變得更加復雜，很難從理論上對應力與變形進行計算分析，而對預應力錨索影響閘墩應力與變形的可能因素成為了主要的研究方向。

多年以來，國內外的學者與工程師對改善預應力閘墩的應力與變形的可能因素做了許多研究，并取得了一定的成果。國際上，預應力閘墩最早在20 世紀50年代末期應用于突尼斯的梅列格溢洪道上。在20 世紀60年代，美國在哥倫比亞河修建瓦那龐溢洪道工程時，采用了14束每束張拉力為2 900 kN 的錨索錨固［1］。隨著有限元方法及計算機技術的發(fā)展，數值模擬技術得到了迅猛發(fā)展，國際上出現大量的商業(yè)數值模擬軟件。其中較為著名的通用大型有限元軟件有ANSYS、ABAQUS、MSC.NASTRAN 和MSC.MARC 等［2-4］。在國內，在閘墩結構優(yōu)化方面，朱暾等［5］提出了閘墩頸部開槽結構，該型式可以顯著提高混凝土的抗裂能力，改善閘墩的應力分布狀態(tài)；胥潤生［6］提出“深槽+錨孔”的結構方式，大大節(jié)省了錨索數量，優(yōu)化了施工步驟；中國水電院提出了一種新的簡支傳力梁結構，使錨索預應力通過傳力梁的支座傳給錨塊，并將預應力轉移到弧門推力作用線附近，使預應力總噸位與弧門推力之比接近1.0。在錨索設計方面，郭宏磊等［7］通過有限元及彈性理論為基礎并結合模型試驗，對錨固區(qū)的開裂部位及應力分布規(guī)律進行研究，提出了一種新型錨塊形式；楊曉紅等［8］對預應力閘墩主錨索的布置方式進行了研究；張發(fā)明等［9］提出了有關預應力錨索設計參數的優(yōu)化方法；李守巨對閘墩裂縫的形成機理及加固措施等進行研究，并提出了合理的預應力錨索加載方案和錨索布置形式；二灘水電站采用了新型的閘墩預應力錨固技術-U 形錨固式［10］；馬吉明等［11］等提出了一種新型的無黏結彎曲預應力錨索結構。

綜上所述，目前對預應力閘墩的研究主要是從改變閘墩的結構設計或預應力錨索的形式、空間布置、加載分級等角度出發(fā)，幾乎沒有考慮過錨索張拉順序對預應力閘墩結構的影響，在施工中也常常被忽略。但隨著預應力閘墩布置錨索數量越來越多，布置形式越來越復雜，錨索的張拉次序將成為影響閘墩結構安全的重要因素。

為了弄清不同錨索張拉次序對閘墩結構的影響，本文提出了一種能夠有效改善閘墩結構受力狀態(tài)的預應力錨索張拉方式——交錯式對稱張拉法。以四川某水庫2 號溢流壩段為例，建立閘墩計算模型，擬從數值仿真的角度分析主、次錨索不同的張拉次序對閘墩結構的影響，并從主、次錨索作用方式的角度對改變錨索張拉次序對閘墩產生影響的機理進行探討。

1 預應力閘墩的模擬方法

1.1 預應力混凝土的模擬

對于有限元建立預應力混凝土結構模型一般有兩種方法。一種是直接用荷載代替力筋影響作用于結構，即為等效荷載法；另一種用不同的有限元單元分別模擬鋼筋和混凝土，可以獲得詳細的預應力混凝土結構力學行為，即為實體力筋法［12］。

等效荷載法將預應力筋與混凝土形成一個整體，無法反映出預應力混凝土結構真正的變形行為；不考慮預應力筋的布置導致張拉的具體過程無法模擬，力筋處的混凝土受力結果也不能保證其可靠性［12］。

實體力筋法將混凝土和錨索分別采用不同的單元模擬，錨索的預應力可以采用降溫法和初應變法進行施加。降溫法需要設置相關單元的實常數，并可以模擬預應力的損失狀態(tài)。初應變法一般不考慮預應力加載過程產生的損失［12］。

本次建模采用實體力筋法建立預應力閘墩模型，并采用降溫法來模擬預應力的施加。

1.2 本構模型

1.2.1 預應力錨索的本構模型

將預應力錨索視為線彈性材料，即假定錨索在加載或卸載中，應力-應變呈線性關系（以錨索的彈性模量E為斜率的直線），其表達式為：

式中：σ為應力；ε為應變；E為錨索的彈性模量。

1.2.2 混凝土的本構模型

將混凝土視為理想彈塑性材料，采用Drucker-Prager 材料模型，即采用Drucker-Prager 準則判別混凝土是否進入塑性狀態(tài)，并采用相關聯的流動法則［13］，其表達式如下：

式中：I1和J2分別為應力張量的第一不變量和應力偏張量的第二不變量，其中參數α和k可以用混凝土的黏聚力C和內摩擦角φ來表示：

1.3 錨索張拉次序的方法

根據預應力閘墩錨索張拉的基本原則：預應力錨索采用分批、分級對稱張拉的方式進行，先張拉次錨索、后張拉主錨索，先張拉監(jiān)測錨索、后張拉非監(jiān)測錨索［14］。本文根據這一基本原則，對預應力錨索的張拉次序擬定兩種不同的張拉形式，分別為行列式對稱張拉、交錯式對稱張拉。

在對稱張拉的基礎上，取對稱區(qū)域的左上角1/4 為例，采用依次張拉的方式對錨索進行張拉［如圖1，左上角1/4 區(qū)域的張拉順序為1→2→3→5→7→9（行式張拉法）或為2→5→9→1→3→7（列式張拉法）］，這種方式為行列式對稱張拉法。

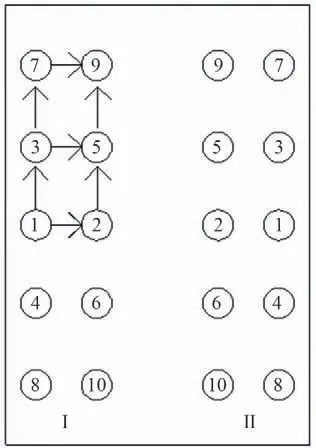
圖1 行列式對稱張拉法示意圖Fig.1 Sketch of determinant symmetric tension method

在對稱張拉的基礎上，取對稱區(qū)域的左上角1/4 為例，采用跳序張拉的方式對錨索進行張拉，張拉的次序為交錯式（如圖2，左上角1/4 區(qū)域的張拉順序為1→2→4→6→7→9），這種方式為交錯式對稱張拉法。

圖2 交錯式對稱張拉法示意圖Fig.2 Sketch of staggered symmetrical tension method

2 工程概況

四川某水庫工程溢流壩段為混凝土重力壩，由5 孔開敞式實用堰組成，建基面高程為336.00 m，最大壩高39.80 m，堰頂高程為350.00 m，閘墩采用預應力閘墩。孔口凈寬14 m，中墩厚為5 m，邊墩厚為4.5 m，每個閘孔設有弧形工作閘門。工作門孔口尺寸為14 m×22 m（寬×高），采用弧形閘門液壓啟閉。該水庫溢流壩段從左至右有1～5 個閘孔，對應閘孔底板分縫為4 個壩段，其中：1號溢流壩段為閘孔1+閘孔2的左側段；2號溢流壩段為閘孔2 右側段+閘孔3 左側段；3 號溢流壩段為閘孔3 右側段+閘孔4左側段；4號溢流壩段為閘孔4右側段+閘孔5。

預應力錨索布置分別為：主錨索單邊閘墩布置2排，內側立面為5 層放射狀布置，外側立面為7 層放射狀布置，總共12 束。單根錨束預應力4 000 kN（永存錨固力），設計張拉力5 000 kN，超張拉力5 500 kN。水平向布置14 根次錨索，單束永存錨固力2 000 kN，設計張拉力2 350 kN，超張拉力2 585 kN。在正常蓄水位350.00 m 情況下，弧門總推力50 000 kN，分攤到兩側的弧門支座推力F均為25 000 kN。

2號溢流壩段預應力錨索采用后裝后張法無黏結預應力施工，分主錨索和次錨索。主錨索順流向、呈放射狀布置，每束主錨索由32 根鋼絞線構成；次錨索垂直于流向水平布置，每束次錨索由14根鋼絞線構成。主錨索張拉力端設在錨塊下游位置，補償張拉力端設在上游預留孔位置，次錨索錨固于錨塊兩側。其中主錨索分為兩組，第一組錨索中心距閘墩迎水面60 cm，共7 束，從上到下編號分別為A1～A7（B1～B7），第二組錨索中心距閘墩迎水面120 cm，共5 束，從上到下編號分別為A8～A12（B8～B12）；次錨索共14束，編號為C1～C14。主錨索剖視圖如圖3，次錨索剖視圖如圖4。

圖3 主錨索布置圖Fig.3 Layout of main anchor cable

圖4 次錨索布置圖Fig.4 Layout of sub-major anchor cable

根據上述錨索布置形式，分別采用行列式對稱張拉與交錯式對稱張拉的方式擬定如下4種張拉方案，其中方案一、二采用行列式對稱張拉法，方案三、四為交錯式對稱張拉法。（根據對稱性以下方案只列出非對稱部分錨索張拉次序）

方案一：

主錨索的張拉次序為：A10→A9→A8→A4→A3→A2→A1

次錨索的張拉次序為：C7→C6→C4→C5→C3→C2→C1

方案二：

主錨索的張拉次序為：A4→A10→A3→A9→A2→A8→A1

次錨索的張拉次序為：C7→C6→C4→C5→C3→C2→C1

方案三：

主錨索的張拉次序為：A4→A10→A3→A8→A1→A9→A2

次錨索的張拉次序為：C7→C3→C5→C6→C4→C1→C2

方案四：

主錨索的張拉次序為：A10→A3→A8→A1→A4→A9→A2

次錨索的張拉次序為：C7→C3→C2→C6→C4→C1→C5

3 不同錨索張拉次序對閘墩結構的影響

本文以四川某水庫溢流壩段2 號溢流壩段為例，采用上述兩種不同的錨索張拉次序方式，擬定4種錨索張拉次序方案，針對2 號溢流壩段的閘墩兩側閘門關閉工況，對不同的錨索張拉次序對閘墩結構的影響進行分析。

3.1 計算模型

根據該水庫2 號溢流壩段設計參數為依據，擬定閘墩兩側閘門關閉的工況施加水荷載、重力荷載以及弧門水推力，建立如圖5 所示有限元模型。該模型利用ANSYS 軟件建模，其中混凝土采用三維實體單元和理想彈塑性材料并采用Drucker-Prager屈服準則，錨索采用桿單元和線彈性材料，模型結構部分共有節(jié)點10 089 個，單元數8 484 個。計算模型具體數值參數如表1所示。

圖5 預應力閘墩的數值模型Fig.5 Numerical model of prestressed gate pier

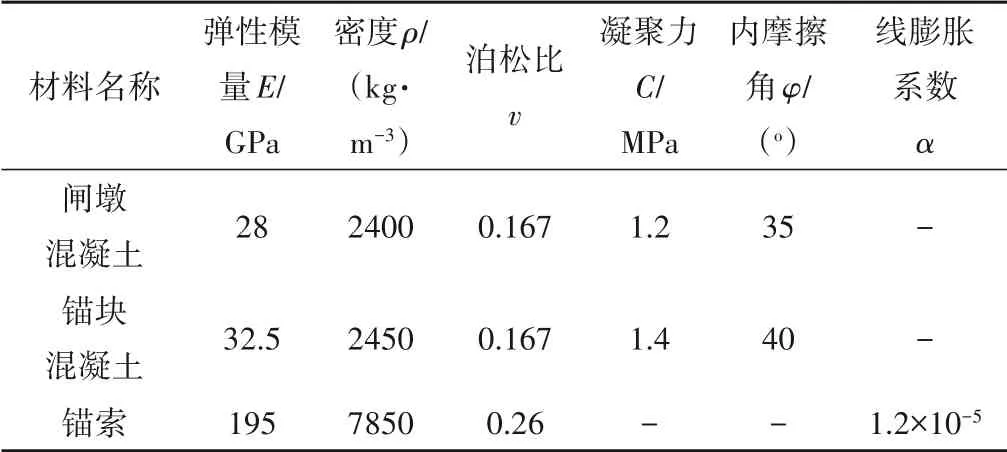
表1 數值計算參數表Tab.1 Parameters for numerical modelling

3.2 不同的錨索張拉次序對錨索應力的影響

圖6～圖8為不同張拉方案下錨索最大應力的變化。圖6為錨索施壓后次錨索最大應力值。圖7～圖8 為錨索施壓后主錨索最大應力值。

圖6 不同方案下次錨索C1～C14的應力變化Fig.6 Stress variation of sub-major anchor cable C1～C14 under different schemes

從圖6 中可以看出，各錨索在不同張拉方案下的最大應力值沒有明顯變化。除了C5 號和C12 號錨索在方案四下的最大應力值比其他方案下的最大應力值大了1%左右，其他次錨索在不同張拉方案下的最大應力值基本一樣，說明改變張拉次序對次錨索的應力影響不大。

從圖7 中的A1～A12 號錨索可以看出，方案一與方案二的不同編號的錨索之間應力值變化不大，但方案一比方案二的同一編號錨索的應力大，而方案三與方案四的不同編號的錨索之間應力值變化較大，方案三與方案四相同編號錨索的應力相差不大。而圖中A8～A12 號錨索，方案一與方案二的不同編號的錨索之間應力值變化較大，且方案一比方案二相同編號錨索的應力值更小，而方案三與方案四的不同編號的錨索之間應力波動不大，方案三與方案四相同編號錨索的應力相差不大。

從圖7～圖8 中可以看出，采用行列式對稱張拉法（方案一、方案二）與采用交錯式對稱張拉法（方案三、方案四）在同一編號主錨索的應力值上有明顯變化，同時不同主錨索之間的應力分布規(guī)律也有變化，說明改變張拉次序對主錨索的應力有較大的影響。

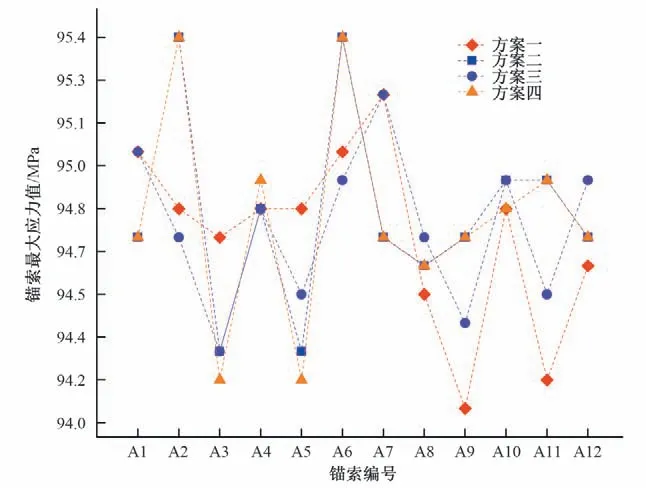
圖7 不同方案下主錨索A1～A12的應力變化Fig.7 Stress variation of main anchor cable A1～A12 under different schemes

圖8 不同方案下主錨索B1～B12的應力變化Fig.8 Stress variation of main anchor cable B1～B12 under different schemes

對比圖7 與圖8，閘墩兩側相對應編號的錨索應力值基本相同，且在同一側的錨索中上下對稱的錨索應力值相差并不大。不同方案下，錨索應力值的區(qū)別主要是非對稱區(qū)域錨索不同張拉次序引起的。

3.3 不同的錨索張拉次序對閘墩應力的影響

圖9為預應力錨索張拉施壓后方案一與方案三閘墩內部的應力等值線圖，等值線的序號后為其所代表的應力數值。從圖9 中不同方案下閘墩的應力等值線圖可以看出，盡管采用了相同的有限元計算模型并施加了相同的荷載，僅在改變錨索的張拉次序的情況下，錨索對混凝土的預壓效果卻產生了差別。以閘墩錨塊為例，方案一的最大拉應力值為2.16 MPa；方案三的最大拉應力值為1.05 MPa。從整體的范圍來看，采用交錯式對稱張拉的方式張拉后，預壓區(qū)內混凝土的拉應力大部分減小到0.5 MPa 以內，而采用行列式對稱張拉的方式張拉后，仍有很大范圍的混凝土拉應力超過1 MPa。同時，方案一的預壓效果主要集中在錨固兩端，對中間部位的混凝土預壓效果較差。而方案三的應力分布更加分散，預壓效果得到了一定的改善。

圖9 方案一與方案三預壓后閘墩內的σ1等值線圖（單位：Pa）Fig.9 Contours of σ1 in the gate pier prestressed by scheme 1 and scheme 3

圖10～圖11 為預應力錨索張拉施壓后，方案二與方案四的主、次錨索錨定面上應力等值線。圖10為次錨索錨定面的應力等值線圖，從圖10 中可以看到，方案二和方案四的應力值與應力分布并沒有明顯的差別，最大拉應力值均在1.05 MPa 左右。圖11 為主錨索錨定面的應力等值線圖，從圖11 中可以看到，方案二的最大應力值和方案四的最大應力值差別明顯變大，方案二的最大拉應力值達到了1.66 MPa，同時有一定范圍的混凝土拉應力超過了1 MPa。方案四的拉應力值明顯更小，最大值為0.78 MPa 左右。同時可以看出，在錨定面上應力主要集中在錨索范圍的邊緣區(qū)域，對于采用兩種不同的張拉次序在次錨索錨定面上應力沒有明顯差別，且應力分布規(guī)律基本相同，而主錨索錨定面上應力出現了明顯變化，方案二的最大應力值比方案四的最大應力值大一倍左右，且方案二的拉應力區(qū)（等值線G所對應的區(qū)域）主要在布置錨索區(qū)域邊緣，方案四的拉應力區(qū)（等值線H所對應的區(qū)域）主要在布置錨索區(qū)域的兩側。

圖10 方案二與方案四預壓后次錨索錨定面上σ1等值線圖（單位：Pa）Fig.10 Contours of σ1 on the anchoring surface of sub-major anchor cable by scheme 2 and scheme 4

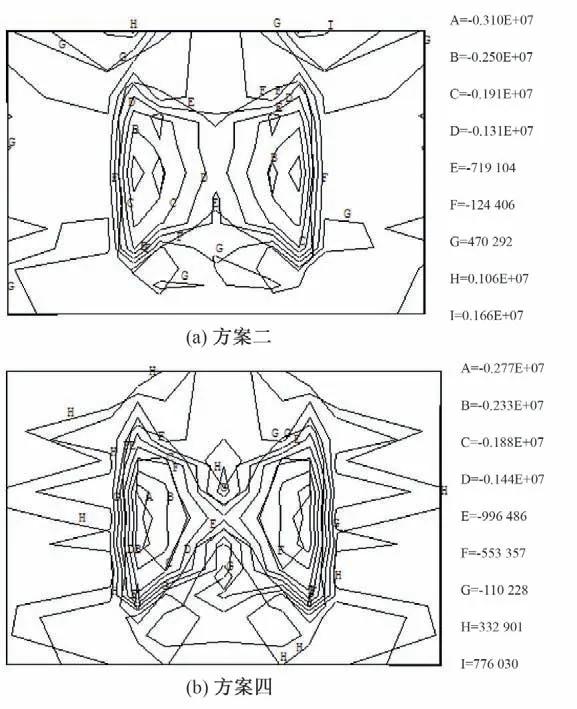
圖11 方案二與方案四預壓后主錨索錨定面上σ1等值線圖（單位：Pa）Fig.11 Contours of σ1 on the anchoring surface of major anchor cable by scheme 2 and scheme 4

圖12為不同方案典型部位的應力值變化圖，根據錨索張拉后閘墩應力分布情況選取典型部位，比較不同方案下的應力值變化。選取應力分布比較集中的部位分別為，閘墩主錨索上游錨固端（節(jié)點號：58208）；閘墩錨塊主錨索錨定面上部（節(jié)點號：53562）；閘墩錨塊主錨索錨定面下部（節(jié)點號：58147）；閘墩錨塊次錨索錨固端上部（節(jié)點號：235650）；閘墩錨塊次錨索錨固端下部（節(jié)點號：235715）。從圖12中不同方案下節(jié)點的應力值變化可以看出，次錨索錨固端上下部位應力值完全一樣，不同方案之間的應力變化不大，變化值都在0.2 MPa 以內；而主錨索上游錨固端的應力值與次錨索錨固端的應力呈現一種對稱分布。在主錨索錨定面下部區(qū)域不同方案的應力值并沒有明顯變化。但是在主錨索錨固端的上部可以看出應力值發(fā)生了顯著改變，從方案二到方案三應力值有一個明顯的下降，說明相比行列式對稱張拉法來說，交錯式對稱張拉法能夠明顯改善閘墩錨塊上部的應力狀態(tài)。

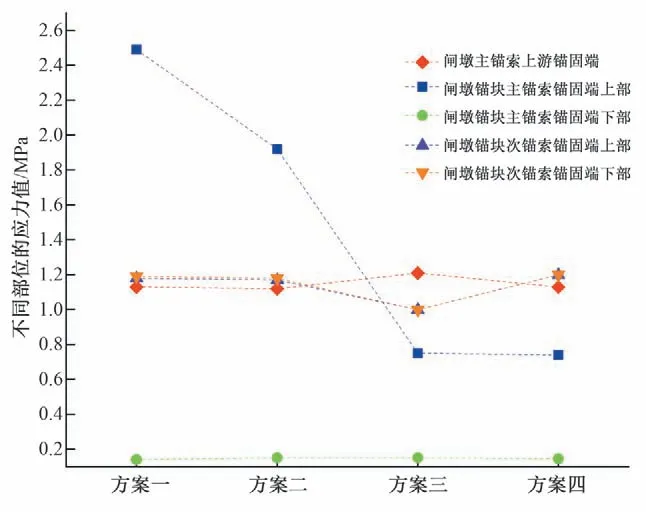
圖12 不同方案下典型部位應力變化Fig.12 Stress changes of typical parts under different schemes

3.4 不同的錨索張拉次序對閘墩變形的影響

圖13～圖15 為不同方案典型部位的位移值隨荷載步的變化圖。根據閘墩位移變化的變化情況選取典型部位，選取主錨索錨固端的中心部位作X向位移分析；選取錨塊主錨索錨定面的下部作Y向位移分析；選取次錨索錨固端的中心部位作Z向位移分析。從圖13～圖15 中可以看到，采用不同張拉次序方案在張拉的過程中閘墩的位移會發(fā)生改變，但是在張拉完成時所有方案的位移值都相同。說明改變錨索張拉次序只會影響張拉過程中閘墩的變形，對閘墩的最終變形影響較小。

圖13 不同方案閘墩X向的位移變化Fig.13 X-direction displacement change of pier in different schemes

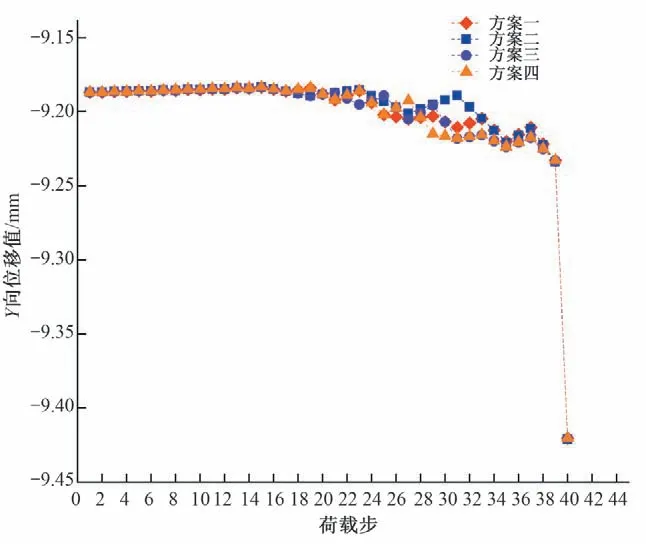
圖14 不同方案閘墩Y向的位移變化Fig.14 Y-direction displacement change of pier in different schemes

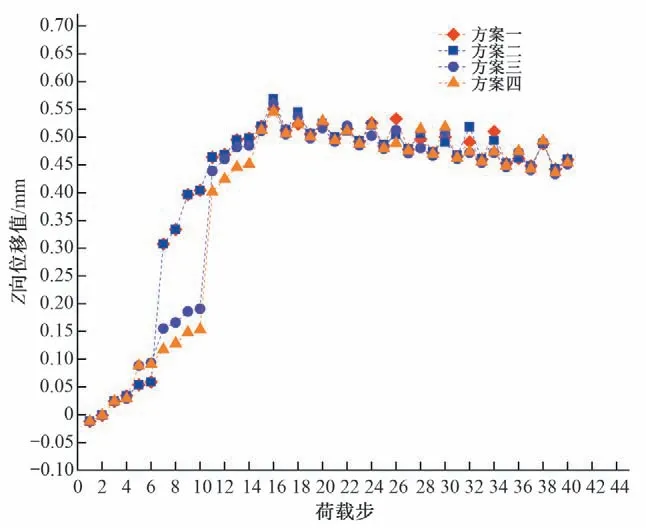
圖15 不同方案閘墩Z向的位移變化Fig.15 Z-direction displacement change of pier in different schemes

3.5 不同的錨索張拉次序對閘墩的應力與變形影響機制的探討

通過上述有限元計算結果可以看出，預應力錨索采用交錯式對稱張拉方式可以使閘墩混凝土的拉應力分布更均勻，從而降低拉應力的最大值，改善閘墩的受力狀態(tài)。結合錨索的應力分布和混凝土的應力與變形變化，對閘墩的影響有以下認識：

（1）改變錨索的張拉次序可能會改變錨索的應力大小，對主錨索而言效果更為明顯，次錨索改變并不明顯。考慮到主、次錨索的布置和作用，推測這種改變效果的差異可能是與錨索的作用點和施加的荷載大小有關。閘墩上主錨索是沿弧門推力方向平行布置，作用點接近弧門推力作用線方向，主要承擔弧門推力。次錨索一般垂直于主錨索布置方向，主要抵消荷載產生的次生拉應力對錨塊的不利影響［15］。在預應力閘墩結構中，主錨索承擔主要的外荷載，張拉力會較大，而次錨索承擔的荷載更小，張拉力也會更小。因此，改變張拉次序對次錨索的影響相對更小。

（2）錨索張拉次序的改變會改變錨索與混凝土的受力狀態(tài)。預應力結構是在結構受到荷載作用之前，對混凝土預壓來發(fā)揮混凝土抗壓強度高的優(yōu)勢，使混凝土處于彈性工作狀態(tài)。相比行列式對稱張拉的方式，交錯式對稱張拉會使錨索來承擔更多的拉應力，從而降低混凝土的拉應力。這樣的應力分布更能充分發(fā)揮兩種材料的特性，錨索可以承受很大的拉應力，而混凝土則要避免受拉。同時，在交錯式對稱張拉后的閘墩，只有小部分的拉應力偏大，且均在1 MPa 左右作用在混凝土集中受壓區(qū)的邊緣，范圍很小。這種應力分布符合結構要求，且對閘墩受力狀態(tài)得到極大的改善。

（3）錨索張拉次序的改變對閘墩最終變形的影響較小。這可能是在錨索預應力、水壓力及結構自重的共同作用，結構絕大部分處于彈性狀態(tài)，在總荷載不變的情況下，錨索張拉次序的改變，只是改變了荷載施加的順序，而對閘墩最終變形的影響較小。

4 結 論

本文以四川某水庫閘墩為例建立預應力閘墩的有限元計算模型，利用兩種不同類型的張拉方式得到了預應力錨索應力、閘墩混凝土應力與預應力錨索張拉次序之間的關系，對比研究后發(fā)現交錯式對稱張拉的這種方式能夠明顯改善結構的受力狀態(tài)。同時，通過對主、次錨索的作用方式和錨索應力、混凝土應力與變形對比，探討了改變錨索次序對閘墩受力影響的作用機理，得到結論如下。

（1）通過改變錨索張拉次序的方法可以有效改善閘墩的受力狀態(tài)。改變預應力閘墩錨索的張拉次序會改變預應力錨索與閘墩混凝土之間的應力分配，從而改善閘墩的受力狀態(tài)。

（2）計算結果表明，采用交錯式對稱張拉法張拉預應力錨索會使錨索承擔的拉應力變大，混凝土承擔的拉應力變小，減輕應力集中的影響。

（3）改變錨索的張拉次序對閘墩的最終變形影響較小。在張拉過程中改變錨索張拉的次序，會導致張拉過程中閘墩變形的改變。但在所有錨索張拉完成后，閘墩的荷載保持一致，最后的變形相差不大。

（4）當閘墩采取無黏結直錨索布置時，采取交錯式對稱張拉的方式會使預應力閘墩的受力更加合理，對拉應力區(qū)的預壓效果更好。但對改變預應力錨索張拉次序對閘墩結構影響的機理還需要進一步深入研究，同時，隨著彎曲錨索的應用，U 形錨索的使用頻率增加，交錯式對稱張拉法同樣對U 形錨索的施工與設計提供了新的思路。