LabVIEW 與 MATLAB 聯合編程在制冷系統故障診斷中的應用

任正雄 韓華 崔曉鈺 卿紅 葉暉云

摘要：制冷系統作為建筑的主要能耗設備，其故障的及時診斷與糾正有助于提高能源利用率，減少對環境的影響。缺乏診斷平臺是制約制冷系統故障智能診斷推廣應用的重要因素之一。基于 MATLAB 軟件強大的數據處理能力和LabVIEW 軟件便捷的虛擬儀器開發功能，進行聯合編程，實現優勢互補，并將粒子群優化（PSO ）算法引入最小二乘支持向量機（LSSVM ），作為故障診斷的內核，建立了制冷系統故障診斷平臺。對離心式冷水機組七類典型故障的診斷實驗結果表明：該聯合編程方法可行，可以實現界面友好、功能豐富、方便快捷的制冷系統故障診斷;所建立的 PSO?LSSVM 模型總體診斷正確率高達99.70%，正常和每類故障的診斷正確率均在99%以上。該平臺具有一定的開放性和擴展性，后續可以根據需要對診斷算法及其他功能模塊進行更改或添加，也可增加不同算法之間的比較分析或集成診斷，改善其靈活性，推進其推廣應用。 LabVIEW 軟件的采用，也為故障檢測與診斷嵌入系統控制提供了可能。

關鍵詞：制冷系統;故障檢測與診斷;最小二乘支持向量機;參數優化;軟件編程

中圖分類號： TB69??? 文獻標志碼： A

Application of LabVIEW and MATLAB hybrid programming to fault diagnosis of refrigeration system

REN Zhengxiong，HAN Hua ，CUI Xiaoyu，QING Hong，YE Huiyun

（School of Energy and Power Engineering/Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in PowerEngineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract：Refrigeration system is the major energy consumption equipment in the building. Timely diagnosis? and? correction? of? faults? is? helpful? to? improve? energy? efficiency? and? reduce? the environmental impact. The lack of fault diagnosis platform is one of the major factors that limited the popularization and application of intelligent fault diagnosis of refrigeration system. Hybridprogramming was adopted by combined MATLAB and LabVIEW with powerful data processing capability and convenient virtual instrument development capability， respectively. Besides，? the introduction of particle swarm optimization （PSO） algorithm into the least squares support vector machine （LSSVM） was used as a fault diagnosis kernel to establish a refrigeration system fault diagnosis platform. Diagnostic experiments on seven types of typical faults in the centrifugal chiller showed that the hybrid programming method was feasible and could realize the fault diagnosis of refrigeration system with a friendly interface and abundant functions in a convenient manner. The diagnosis accuracy of PSO-LSSVM model was as high as 99.70%， and the accuracy of normal and each fault exceeded 99%. The platform is open and extensible for the modification and integrationof diagnostic? algorithms? and? other? functional? modules? as? required. Comparative? analysis? or integrated? diagnosis? can? be? included? as? well. The? adoption? of LabVIEW? also? provides? the possibility of embedding fault diagnosis into system control.

Keywords：refrigeration? system; fault? detection? and? diagnosis; least? squares? support? vector machine; parameter optimization; software programming

故障檢測和診斷（fault detection and diagnosis， FDD ）技術在核反應堆、國防、化工、航空航天等多個領域得到了廣泛應用，并取得良好的經濟和社會效益[1?4]。但是該技術在制冷系統的實際應用還沒有得到充分開發，目前大部分在制冷系統中應用的 FDD 功能依然采用低效能的專家系統進行經驗診斷[5]。隨著人工智能的發展，一些 FDD 研究通過采用機器學習或深度學習方法已經得到高精度、高性能的新模型，例如：神經網絡[6]、最小二乘支持向量機[7]等，但是由于FDD 開發人員面臨著多種技術和市場壁壘等問題，基本上沒有出現適合這些模型的商業軟件。

為了推進 FDD 技術在制冷系統中的實際應用，本文提出將粒子群優化（ particle swarm optimization ，PSO ）與最小二乘支持向量機（least squares support vector machine ，LSSVM ）相結合的診斷策略[8]，并基于 LabVIEW 與 MATLAB軟件聯合編程，初步開發一套制冷系統 FDD 平臺。利用 LabVIEW 軟件的可視化編程功能對主界面、圖形顯示和各種模塊進行綜合設計，并將 MATLAB 軟件強大的數值運算能力用于 FDD 模型訓練和故障診斷，通過聯合編程實現高性能故障診斷模型的便捷應用[9?10]。采用離心式冷水機組的故障模擬數據進行實驗驗證，檢測 PSO?LSSVM 模型的診斷性能，并評估聯合編程的可行性及平臺的各項功能。

1故障診斷模型

1.1最小二乘支持向量機

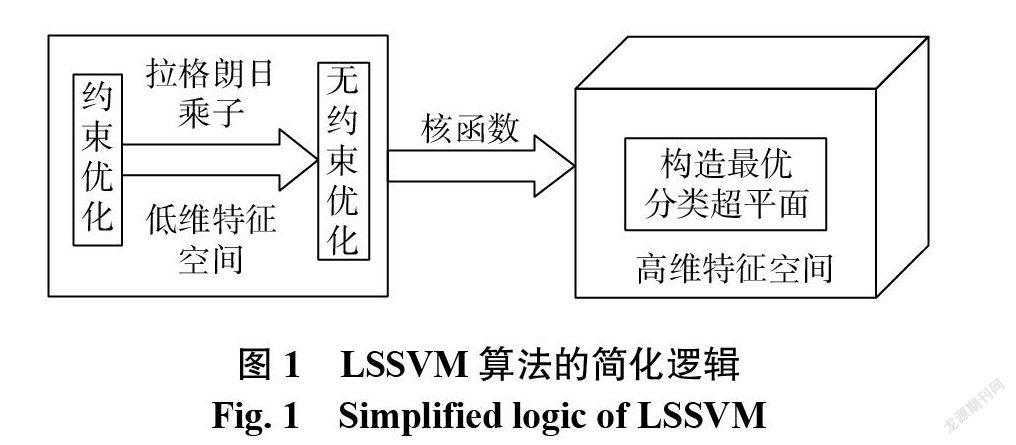
LSSVM 算法是支持向量機（ support vectormachine， SVM ）算法的改進[11]，該算法在制冷系統故障診斷中表現優異。LSSVM 算法的簡化邏輯如圖1所示。該算法通過在低維特征空間中引入拉格朗日乘子，將約束優化問題轉變成無約束優化問題，先在運算更簡便的低維特征空間完成計算，然后通過核函數將輸入空間映射到高維特征空間，最后在高維特征空間構造出最優分類超平面。

最小二乘支持向量機算法的分類優化問題表達式為

式中： w 為權向量;i為松弛因子，可以度量一個數據點對模式可分的理想條件下的偏離程度; b 為偏置值;yi為輸出數據（制冷系統故障類別）;xi 為輸入數據（表征制冷系統故障狀態的參數）;牽（x）為非線性映射函數; n 為樣本點數目;γ為正則化因子，屬于可調參數，用于調節 LSSVM 置信范圍和經驗風險的比例，實現結構風險最小化。

當γ取值較小時，表示對超出誤差范圍的樣本點的懲罰程度不足，模型的復雜性低而經驗風險高，會造成機器的欠學習現象;反之，當γ取值較大時，對訓練樣本點誤差的懲罰加大，則會出現過學習現象[12]。因此，γ過大或過小都會使模型的泛化性能變差。

引入拉格朗日乘子αi（ i =1，2，3，···，n ）進行無約束優化，進而提高運算速度。采用核函數進行高維映射，利用Karush?Kuhn?Tucker （ KKT ）[13]優化條件及 Mercer 條件[14]求解，得出分類模型為

式中：sgn（u）為符號函數，當 u ≤0，則sgn（u）=?1，當 u >0，則sgn（u）=1;K （x， xi）為滿足 Mercer 條件的核函數。

本文選取高斯徑向基核函數（ radial basis function，RBF ）[15]，即

K （x， xi）= exp （?）

式中：σ為核參數，它決定了數據映射到新的特征空間后的分布，σ越大，支持向量越少，σ越小，支持向量越多，支持向量的個數影響訓練與預測的速度，從而影響模型的泛化性能。

1.2粒子群優化算法

PSO 是一種基于種群的搜索算法，每個個體在多維搜索空間中被視為無體積的粒子（一個點），粒子運動情況如圖2所示。每個點都具有特定位置和速度，按照一定慣性運動。解空間中存在個體最優和種群最優，每個粒子都會受到自我認知和群體的影響，并根據式（4）、（5）更新速度和位置，不斷改變運動方向并向最優位置運動，經過多次迭代后即可尋得最優解。

式中：i =1，2，…，N，N 為群體中粒子總數;下標“i”表示第i個粒子;下標“d ”表示粒子的第 d 維，即優化的第d 個參數; t 為迭代次數;pid （t）為第i個粒子在迭代到第 t 代前搜索到的最優位置;pgd（t）為整個群體搜索到的最優位置;c1、c2均為加速因子，分別代表粒子向自身學習的成分和向群體學習的成分，本文取c1=1.5， c2=2;r1（t）、r2（t）均為服從（0，1）區間上均勻分布的隨機數;vid為速度，被限制在區間[ Vmin， Vmax]內（ Vmin、 Vmax 分別為最小和最大速度），避免因粒子速度過大而跳過最優解或速度過小導致粒子的全局搜索能力降低;w 為慣性權重，用來平衡算法的局部搜索能力與全局搜索能力。

式中：tmax為最大迭代次數;wmax、wmin分別為 w 的最大值和最小值。

1.3 PSO?LSSVM 模型

LSSVM 的建模過程中需要設定兩個關鍵參數的值：核參數σ和正則化因子γ，統稱為超參數，它們直接影響 LSSVM 模型的泛化性能和魯棒性。采用 PSO 算法進行超參數優化，通過迭代選擇最優超參數，提高模型分類正確率和故障診斷性能。優化過程需要確定超參數的表示方法和粒子適應度函數。需要優化的超參數有兩個，因而搜索空間的維數為2（d =2）。每個粒子表示為 Xi=（σ，γ），粒子群 p1優化參數σ，粒子群 p2優化參數γ[16]。適應度用于評價粒子所處位置的優劣。適應度函數f（x）越小，適應能力越強。本文采用訓練樣本的均方根誤差（ MSE ）?e作為適應度函數，即

式中：yib為訓練樣本的真實標簽;yb為訓練樣本的預測標簽。

根據以上分析，可建立 PSO?LSSVM 模型。圖3為基于 PSO?LSSVM 算法的制冷系統故障診斷框架。

PSO?LSSVM 模型故障診斷過程為：

（1）數據預處理。導入數據，將數據分為訓練集和測試集兩部分，實驗數據之間可能存在數量級的差異，影響模型的診斷性能，需要對數據進行歸一化處理。

（2）優化超參數。

步驟1：初始化群體大小，設置最大迭代次數和粒子的速度和位置;

步驟2：構建 LSSVM模型;

步驟3：根據式（7）計算每個粒子的適應度;

步驟4：更新個體極值和全局極值;

步驟5：根據式（4）、（5）更新每個粒子的速度和位置，根據式（6）更新慣性權重;

步驟6：重復步驟2～6，直到滿足終止條件;

步驟7：終止算法，給出最優超參數。

（3）訓練和測試。利用最終得到的超參數訓練 LSSVM 模型，通過交叉驗證進行評估。將測試集導入模型中，得到故障診斷結果，進而分析模型性能。

2聯合編程與 FDD 平臺設計

MATLAB 軟件具有強大的科學計算功能和大量穩定，可靠的工具箱，其在故障診斷中應用較廣，可有效實現各種數據挖掘及智能算法。但 MATLAB 環境界面不夠友好、易用，因此，引入擅長虛擬儀器設計的 LabVIEW 以彌補其不足，并為 FDD技術與系統控制相結合提供可能。

LabVIEW 與 MATLAB 數據互通的方法有多種[17]，本文采用 MATLAB Script 節點[18]進行聯合編程。 LabVIEW 與 MATLAB 數據轉換流程如圖4所示。MATLAB Script 節點（以下稱腳本節點）的作用是直接調用已安裝的 MATLAB 程序，并在 LabVIEW 環境下運行已建立的 PSO?LSSVM 模型。該方法容易實現，打開腳本的速度快，能夠滿足多輸入多輸出，一次處理的信息量大，方便快捷。

在聯合編程過程中，所有的數據交互均需通過腳本節點實現。圖5以其中一個節點為例，闡釋聯合編程方法。主要步驟為：

（1）在 LabVIEW環境中找到腳本節點（圖5中的 A 部分），并在框圖中進行設置。算法可以從 MATLAB 中導入，也可以直接在節點中編寫;

（2）設置節點的輸入和輸出。輸入為模型訓練數據（condata），輸出為模型訓練仿真后得到的結果;

（3）運行程序。腳本節點開始調用 MATLAB 程序，將輸入數據分配給 PSO?LSSVM 模型，并運行程序。訓練和仿真完成后，將結果傳輸并分配給節點的輸出：混淆矩陣（ConfMat ）和正確率（Accu ）;

（4）在 LabVIEW軟件中，將腳本節點的輸出可視化，根據用戶需求進行進一步分析，如圖5中的 B 部分所示。同時，設計多個子 VI（virtual instrument）以實現多種功能并簡化程序框圖。

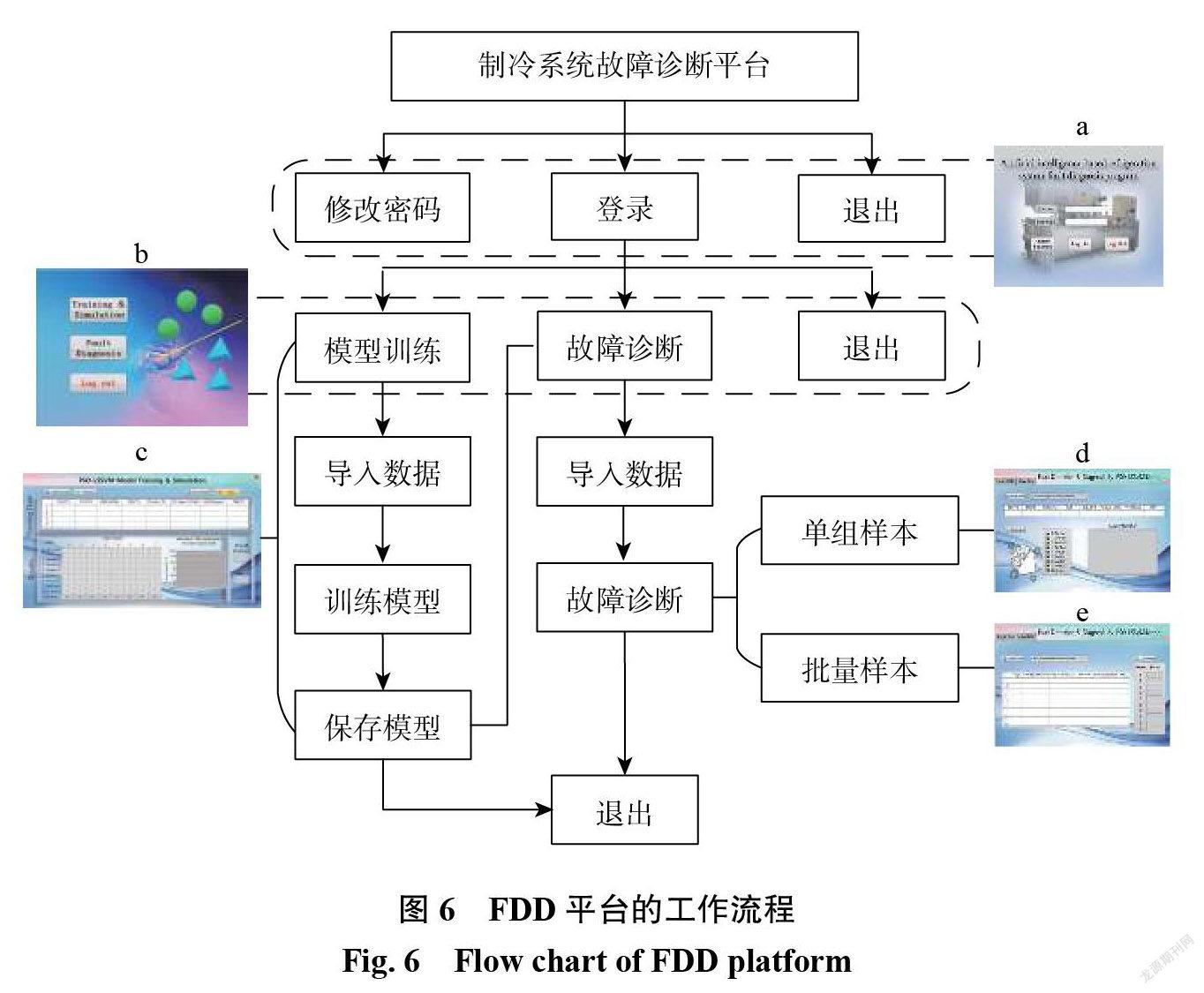
基于此聯合編程思想，初步搭建了一個制冷系統 FDD 平臺。開發環境為：Windows 10操作系統， MATLAB 9.4（ R2018a）、 LabVIEW2018。圖6為該平臺的工作流程。不同功能模塊對應不同的界面窗口，包括登錄模塊 a、功能選擇模塊 b、模型訓練模塊 c 和故障診斷模塊 d 和 e。平臺整合了用戶管理，并將 PSO?LSSVM 模型訓練與故障診斷分開，用戶可以根據不同需求進入不同模塊。模型訓練模塊可以展示訓練結果并保存模型;故障診斷模塊根據數據量不同分為單組樣本診斷與批量樣本診斷，既保證功能完善，又實現可視化，提高效率。

3實驗驗證

將 PSO?LSSVM 模型嵌入 FDD 平臺中進行實驗，通過平臺的分析運算功能評估模型的性能，同時采用該模型運行平臺的各模塊，進一步驗證平臺設計優劣以及通過聯合編程思想推進制冷系統 FDD 技術實際應用的可行性。

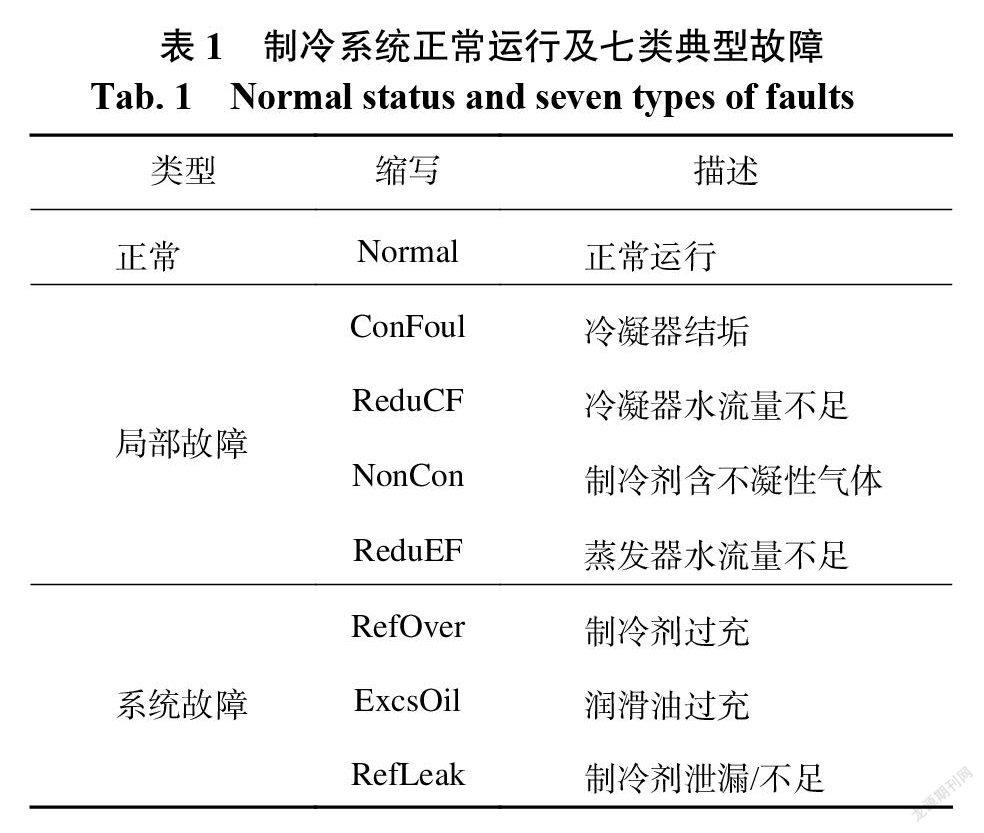
首先，從美國采暖制冷與空調工程師學會（ ASHRAE ） RP?1043離心式冷水機組故障模擬實驗數據庫[19]中，隨機抽取8000個樣本用于模

型訓練，4000個樣本用于模型測試，抽取1個樣本和10個樣本分別用于單組樣本和批量樣本故障診斷。數據共有八類，包含正常運行和七類典型故障，如表1所示。

在平臺的模型訓練模塊（圖6c）中訓練 PSO?LSSVM 模型，運行結果如圖7所示。界面上直觀展示了模型的混淆矩陣、性能直方圖、每類故障的診斷正確率、整體診斷正確率和耗時。可見，模型訓練時間為2580 s，所有類別的總體診斷正確率達到99.70%，正常和每類故障的診斷正確率均在99%以上，而ConFoul和ReduCF的診斷正確率甚至高達100%。從圖7中的性能直方圖可看出，系統故障的診斷正確率較高，但都低于局部故障的，原因在于系統故障對制冷系統的參數影響范圍較大且較為復雜，易與其他故障混淆，難以被正確檢測和識別，從而影響整體診斷正確率。

依托較高性能的 PSO?LSSVM 模型對平臺的故障診斷及其他模塊進行測試。圖8（a）為用于診斷單組樣本的界面，上部是診斷數據信息，下部是診斷結果，以亮燈并發出報警鈴的形式展示，并在右側顯示相應故障的征兆、帶來的影響及可能的維修建議。圖8（b）為批量樣本故障診斷的結果，主要展示數據信息及相應的診斷結果，點擊故障，同樣可以展示該故障的相關信息。

此外，采用120?ton 螺桿冷水機組的故障模擬實驗研究[20]的實際運行數據對該平臺的診斷性能做進一步驗證。由于條件限制，該研究只模擬了 Normal、RefLeak、RefOver三類，包括兩類故障系統故障，運行結果分別如圖9、10所示。 FDD 平臺可以較好地處理實際數據，對于不同類型冷水機組的數據，PSO?LSSVM 模型依然有較好的診斷性能，總體診斷正確率為98.23%。從性能直方圖中可以看出，RefOver的診斷正確率達到100%，平臺各功能模塊均可正常運行。

綜上所述，PSO?LSSVM 模型的診斷性能優良，依托 FDD 平臺可以方便、快捷地實現各種功能，且直觀易操作，達到了設計要求。如果模型預先進行線下訓練，則可實現在線診斷，且準確、高效。

4結論

本文基于 LabVIEW 與 MATLAB 聯合編程的 MATLAB Script 節點技術，開發了一套界面友好、體現人機交互的制冷系統 FDD 平臺，可以方便、快捷地實現故障診斷，并在相對直觀、美化的界面展示結果。充分利用并發揮了 MATLAB 軟件強大的數據處理功能，以及 LabVIEW 軟件的圖形化編程特點和圖像處理功能。該平臺集成了用戶權限管理、數據讀取、模型訓練及保存、多樣化結果展示、故障診斷及報表存儲等功能。

作為診斷內核的 PSO?LSSVM 模型，可在較短時間內完成訓練，實現制冷系統七類典型故障的檢測與診斷，總體診斷正確率高達99.70%，正常和每類故障的診斷正確率均在99%以上，性能優良。采用另一臺不同類型冷水機組故障模擬實驗數據再次進行驗證的結果顯示，平臺各功能模塊均可正常運行，診斷結果較佳。

另外，該平臺亦具有一定的開放性和擴展性。在后續的開發中，可以根據需要對診斷算法及其他功能模塊進行更改或添加，也可增加不同算法之間的比較分析或集成診斷，改善其靈活性，并實現操作界面及結果展示的中英文語言切換，推進其推廣應用。 LabVIEW 軟件的采用，為 FDD 技術嵌入系統控制提供了可能。

參考文獻：

[1] 許明軒.飛機航電系統故障分析方法與故障診斷技術研究[J].中國設備工程， 2018（14）：96-97.

[2] 許偉， 馮武衛， 袁躍峰， 等.船用機械設備故障診斷系統研究與開發[J].機電工程 ， 2014， 31（10）：1291-1295， 1323.

[3] 張霄，錢玉良， 邱正， 等.基于蜻蜓算法優化 BP 神經網絡的燃氣輪機故障診斷[J].熱能動力工程， 2019， 34（3）：26-32.

[4] 杜奕， 唐洪， 丁家滿， 等.一種基于概率盒?PSO?SVM的滾動軸承故障診斷方法[J].上海理工大學學報 ， 2018， 40（1）：76-83.

[5] GRANDERSON J， SINGLA R， MAYHORN E， et al.Characterization? and? survey? of? automated? fault detection? and? diagnostics? tools[R]. Berkeley，? CA： Lawrence Berkeley National Laboratory， 2017.

[6] LIANG Q Q， HAN H， CUI X Y， et al. Comparativestudy? of? probabilistic? neural? network? and? backpropagation network for fault diagnosis of refrigerationsystems[J]. Science and Technology for the Built Environment， 2018， 24（4）：448-457.

[7] HAN H，? CUI X Y，? FAN Y Q，? et al. Least squaressupportvector machine （LS-SVM）-based chiller fault diagnosis? using? fault? indicative? features[J]. Applied Thermal Engineering， 2019， 154：540-547.

[8] 趙莉華， 張亞超， 金陽， 等.基于 LabVIEW 和Matlab虛擬實驗室的實現[J].實驗室研究與探索 ， 2014， 33（4）：62-64，67.

[9] 裴鋒 ， 楊萬生. LabVIEW 與 MATLAB 混合編程[J].電子技術應用， 2004， 30（3）：4-6.

[10]李建強， 張瑩瑩， 牛成林.基于 PSO?LSSVM 模型的火電廠煙氣含氧量預測[J].熱能動力工程 ， 2018，33（7）：49-55.

[11] SUYKENS J A K， VANDEWALLE J. Least squaressupport vector machine classifiers[J]. Neural Processing Letters， 1999， 9（3）：293-300.

[12] CHAMKALANI A， ZENDEHBOUDI S， BAHADORIA， et al. Integration of LSSVM technique with PSO to d etermine? asphaltene? deposition[J]. Journal? of? Petro- leum Science and Engineering， 2014， 124：243?253.

[13]吳崇明， 王曉丹， 白冬嬰， 等.利用 KKT 條件與類邊界包向量的 SVM 增量學習算法[J].計算機工程與設計， 2010， 31（8）：1792-1794， 1798.

[14] FLETCHER R. Practical methods of optimization[M].Chichester： Wiley， 1987.

[15]顧燕萍， 趙文杰， 吳占松.最小二乘支持向量機魯棒回歸算法研究[J].清華大學學報：自然科學版 ， 2015， 55（4）：396-402.

[16]鄭含博， 王偉， 李曉綱， 等.基于多分類最小二乘支持向量機和改進粒子群優化算法的電力變壓器故障診斷方法[J].高電壓技術， 2014， 40（11）：3424-3429.

[17]黃世奎 ， 彭宇寧 ， 謝樹平 ， 等. LabVIEW 與Matlab/Simulink 混合編程方法及應用[J].實驗室研究與探索， 2009， 28（7）：67-71.

[18]王后能， 宋杰. LabVIEW 嵌入Matlab腳本節點的電機轉速控制系統仿真[J].武漢工程大學學報， 2015， 37（8）：69-74.

[19] COMSTOCK? M? C，? BRAUN? J? E. Development? ofanalysis tools for the evaluation of fault detection and diagnostics in chillers[R]. West Lafayette， IN： PurdueUniversity， 1999.

[20] FAN? Y? Q，? CUI? X? Y，? HAN? H，? et? al.Chiller? faultdetection anddiagnosis by knowledge transfer based on? adaptive? imbalanced? processing[J]. Science? and? Technology for the Built Environment， 2020， 26（8）：1082-1099.