鉆孔承壓水頭簡易測量與承壓水Q-S曲線的關(guān)系

陳新攀

(紫金礦業(yè)集團(tuán)股份有限公司，福建 廈門市 361006)

礦產(chǎn)資源多深埋于地下，其開發(fā)和利用與地下水密切相關(guān)。地下水賦存于含水層中。巖層按其滲透性可分為透水層和不透水層。飽含水的透水層是含水層，不透水層稱為隔水層[1]。礦床開采涉及的地下水屬性通常包括水量、水質(zhì)、水位（水壓）等特征。規(guī)范中對地質(zhì)勘查階段的水文地質(zhì)孔要求全部開展分層靜止水位觀測工作，對單一含水層（組）的鉆孔全部需測定終孔穩(wěn)定水位[2]。

在地質(zhì)勘查工作中，在井巷施工的鉆孔常見地下水涌出孔口的現(xiàn)象，但常由于壓力表安裝不便或圍巖破碎導(dǎo)致地下水從井管周圍滲出，導(dǎo)致無法用壓力表進(jìn)行水壓測定。本文結(jié)合多年的一線工作經(jīng)驗(yàn)以及水力學(xué)基本知識，對采用多組承壓水頭與流量數(shù)據(jù)推測穩(wěn)定承壓水頭法進(jìn)行了分析，以期為鉆孔涌水的處理提供解決方法。

1 鉆孔承壓水頭簡易測量

在地質(zhì)勘查過程中，特別是井巷內(nèi)施工的鉆孔，常見地下水涌出的現(xiàn)象。鉆孔承壓水頭的測量通常采用壓力表測壓法，而實(shí)際過程中，由于鉆探施工對孔口附近的地面破壞較大，關(guān)閉水閥，回壓地下水時(shí)，大量的地下水容易從破碎地面或套管縫隙中涌出，造成測得的水壓值偏小，誤差較大。

水文地質(zhì)工作者一般采用接桿測流量和桿長法測得多組流量和桿長值，再通過圖解法簡單計(jì)算穩(wěn)定水頭。由于接桿測流量對水壓的影響相對較小，對地面和套管止水的要求相對較低，具有較強(qiáng)的操作性，特殊情況下常替代壓力表測量法。具體操作如下。

（1）根據(jù)鉆孔水文編錄求得孔口出水位置與承壓含水層頂板距離Z0，測得穩(wěn)定后的流量Q0；

（2）接一根鉆桿，桿長L1，則孔口位置計(jì)為Z1=Z0+L1，測得穩(wěn)定后的流量Q1；

（3）接第二根鉆桿，桿長L2，則孔口位置計(jì)為Z2=Z0+L1+L2，測得穩(wěn)定后的流量Q2；

（4）接第三根鉆桿，桿長L3，則孔口位置計(jì)為Z3=Z0+L1+L2+L3，測得穩(wěn)定后的流量Q3。

其中，穩(wěn)定的流量Q為孔口流量與孔口周圍滲水量的總和，穩(wěn)定時(shí)間與穩(wěn)定流抽水試驗(yàn)的要求一致。

機(jī)臺塔高通常最多只允許續(xù)接至3 根鉆桿，實(shí)際操作中為了擬合計(jì)算準(zhǔn)確性，通常需接2 根或3根桿。測得多組Z、Q數(shù)據(jù)，以一次函數(shù)關(guān)系進(jìn)行擬合，求得Q為0 時(shí)的Z值，此時(shí)，Z值表示測壓管內(nèi)流量為0 的位能，即為承壓水終孔穩(wěn)定水頭值。

2 承壓水Q-S 曲線關(guān)系

2.1 裘布依井流理論與承壓水Q-S 曲線關(guān)系

根據(jù)裘布依完整井承壓水井流理論，對裘布依完整井承壓水公式進(jìn)行變形整理，可得到承壓水公式為：

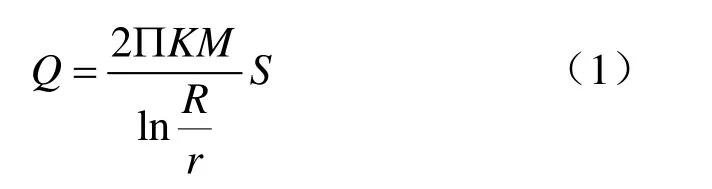
式中，Q為流量，m3/d；K為承壓含水層的滲透系數(shù)，m/d；M為承壓含水層厚度，m；r為抽水井井徑，m；S為抽水井水位降深，m；R為承壓水或潛水的影響半徑（實(shí)際計(jì)算中以抽水井中心至降深為0 位置的距離為影響半徑；但裘布依井流理論的影響半徑實(shí)質(zhì)上是含水層的補(bǔ)給半徑，在此邊界上始終保持常水頭[3]，因此理論曲線計(jì)算時(shí)R值為定值），m。

式（1）中K、M或H、r和R均為固定值，Q、S為未知值，則式（1）中Q與S呈Y=aX的正比例函數(shù)關(guān)系，a為常數(shù)。《專門水文地質(zhì)學(xué)》中對穩(wěn)定流抽水試驗(yàn)承壓水（或厚度很大、降深相對較小的潛水井流）完整井Q?S關(guān)系概化為Q=aS的正比例函數(shù)關(guān)系[4]。

因此，接桿測量位置高程Z和流量Q關(guān)系為：

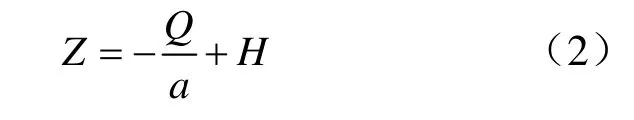
式中，H為總水頭。兩組及以上的Q、Z值即可求得該二元一次式，即求得終孔穩(wěn)定水頭H值，如圖1 所示。

2.2 伯諾里能量方程與承壓水Q-S 關(guān)系

滲流的基本理論中，根據(jù)伯諾里能量方程可得出任一點(diǎn)處液體的總水頭為：

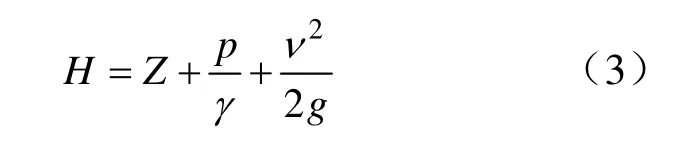
式中，Z為位置水頭，代表單位重量液體所具有的位能，m；P為滲流壓強(qiáng)，m；γ為水的容重；ν為水流的實(shí)際速度，m/s；為單位重量液體所具有壓能；為測壓水頭，為動能，m。

假定鉆孔揭露完整承壓水含水層過程極速，則揭露前后地下水的伯諾里能量方程可概化為如下。

（1）鉆孔揭露之前，承壓含水層各位置的測壓管水頭大小相同，承壓水近似不流動或動能近似為0。

（2）揭露后，地下水從鉆孔四周的承壓含水層向孔內(nèi)流動，并逐漸向上運(yùn)移至流速為0 的位置水頭Z處，承壓含水層也逐漸重新達(dá)到平衡，各位置測壓管水頭均相同。

（3）當(dāng)孔口低于流速為0 的位置水頭Z處時(shí)，地下水從鉆孔內(nèi)涌出，此時(shí)，降深為S，地下水涌出量為Q，整個(gè)地下水系統(tǒng)能量方程可重新定義（見圖2）：地下水從影響半徑R處（斷面1）運(yùn)移至井徑r邊緣（斷面2）處，該過程損失了水頭hw1-2值，剩余總水頭值H2；地下水由井徑r邊緣（斷面2）進(jìn)入井內(nèi)部，繼而向上運(yùn)移至出水口位置（斷面3），出水口孔壁壓力為0，則由斷面1 至斷面3 的伯諾里能量方程可表達(dá)為：

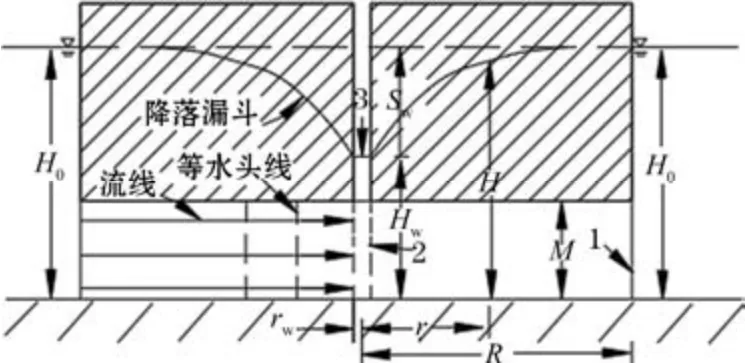
圖2 承壓水完整井流伯諾里能量方程示意圖

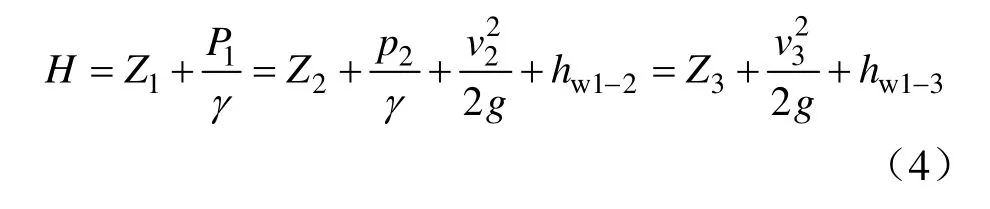
代入Q=Av（A為過水?dāng)嗝婷娣e），得：

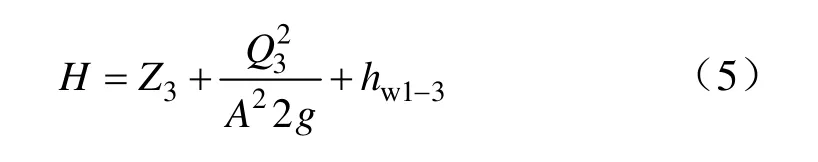
經(jīng)變換得：

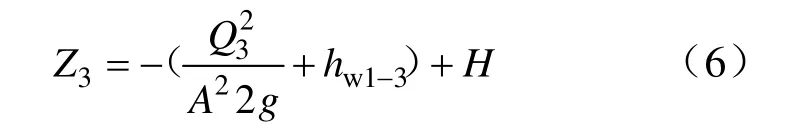
由式（5）可知，位置水頭Z與流量Q2成反比，Z與水頭損失hw1-3成反比。由于動能轉(zhuǎn)化為位能的轉(zhuǎn)化比極小（v=1 m/d≈0.028 cm/s，流速水頭等于3.9×10?7cm）[5]，因此，地下水從斷面1 到斷面3的能量轉(zhuǎn)換為以水頭損失為主。承壓水完整井中，當(dāng)流量Q接近0 時(shí)，降深接近0，水頭損失亦越少；反之亦然。總體上，位能Z與Q2及能量損失hw成反比，呈現(xiàn)出的二元函數(shù)特征，由于能量損失hw和流量、Z的數(shù)學(xué)關(guān)系十分復(fù)雜，其函數(shù)關(guān)系難以定義，在實(shí)際運(yùn)用過程中，需要通過經(jīng)驗(yàn)公式進(jìn)行簡化。

2.3 抽水試驗(yàn)規(guī)程中的Q-S 關(guān)系

《水利水電工程鉆孔抽水試驗(yàn)規(guī)程》中規(guī)定，當(dāng)抽水試驗(yàn)關(guān)系曲線Q-S呈曲線時(shí)，可采用一個(gè)高次方多項(xiàng)式表示，且通常采用4 組Q-S抽水試驗(yàn)數(shù)據(jù)進(jìn)行簡化計(jì)算，如下式：

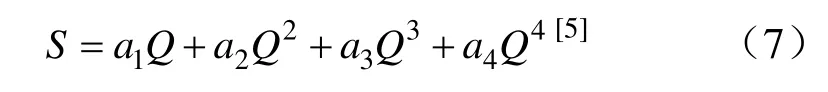
式中，a1、a2、a3和a4均為待定系數(shù)，且采用插值均差法求Q—S多項(xiàng)式及其待定參數(shù)。代入S=H?Z，得：

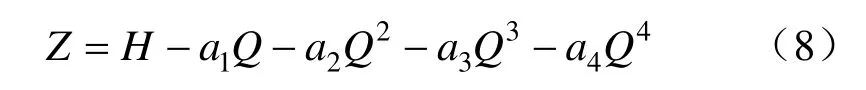
2.4 幾種擬合法分析

（1）根據(jù)裘布依完整井承壓水井流理論，承壓水鉆孔出水流量Q和位置高程Z關(guān)系式可表示為：，Q與Z呈一次函數(shù)關(guān)系。

（2）根據(jù)伯諾里能量方程，位能Z與流量Q的關(guān)系式可以表示為：與Q、Z呈較為復(fù)雜的關(guān)系。

（3）根據(jù)《水利水電工程鉆孔抽水試驗(yàn)規(guī)程》（SL320-2005）相關(guān)經(jīng)驗(yàn)公式顯示，Z=-a1Qa2Q2-a3Q3-a4Q4+H。

分析上述3 種函數(shù)關(guān)系可知，伯諾里能量方程從水力學(xué)基本原理角度對鉆孔承壓水涌水位能與流量關(guān)系進(jìn)行了分析，裘布依完整井承壓水井流理論則在穩(wěn)定流理論的前提下對Q和Z關(guān)系進(jìn)行了探討，而 《水利水電工程鉆孔抽水試驗(yàn)規(guī)程》中的公式則是一種具體的Z?Q關(guān)系曲線的經(jīng)驗(yàn)公式。

同時(shí)，規(guī)程的經(jīng)驗(yàn)公式中，當(dāng)除去a2、a3和a4時(shí)，可簡化為Z=H?a1Q，該式與裘布依完整井承壓水井流公式一致，可見，后者為前者的簡化版。結(jié)合圖1 可知，Z?Q擬合曲線，可簡化為Z與Q的高次方多項(xiàng)式，并且這個(gè)多項(xiàng)式以Z?Q的一次函數(shù)關(guān)系為上限，分布于該一次函數(shù)的左下方。因此，Z?Q一次函數(shù)擬合計(jì)算時(shí)所得Z值為其理論的最大值。

2.5 誤差分析

（1）實(shí)際抽放水過程中，在井管內(nèi)測得的水位降深還包括另外兩個(gè)部分，一是水以高速穿過濾水管時(shí)的水頭損失，二是井管內(nèi)部水向上運(yùn)動到水泵進(jìn)水閥時(shí)的水頭損失[6]。因此，實(shí)際測得的降深值往往小于理論的水頭損失，這將導(dǎo)致擬合的Z值偏小。此外，水井結(jié)構(gòu)，成井工藝及水井附近地下水三維流動都會對Q?S曲線產(chǎn)生影響[6]。

（2）Q?Z擬合過程中，Q、Z表征的狀態(tài)與穩(wěn)定流抽水試驗(yàn)要求一致，必須達(dá)到穩(wěn)定狀態(tài)的流量，而實(shí)際測量流量時(shí)，往往接桿后地下水整個(gè)流態(tài)未達(dá)穩(wěn)定狀態(tài)就測量流量，所測得的Q值往往偏大，導(dǎo)致擬合的Z值偏小。

3 結(jié)論

在鉆孔施工過程中，對于無法直接采用壓力表測量承壓水頭的鉆孔，可以采用接鉆桿測得多組流量和桿長值，再通過Z?Q一次函數(shù)和Z?Q高次方多項(xiàng)式擬合，其中，一次函數(shù)擬合結(jié)果宜作為最大的控邊值，該方法具有一定的可操作性，在一定情況下可以替代壓力表測量法擬合計(jì)算穩(wěn)定水頭。