疊箱式模塊化建筑內力計算方法研究

赫連光澤，周學軍，王振

(山東建筑大學 土木工程學院，山東 濟南 250101)

0 引言

模塊化建筑是一種集成化程度較高的裝配式建筑，已經成為新型建筑技術的主要發(fā)展方向之一[1]。疊箱式模塊化建筑是由若干個模塊單元堆疊而成的裝配式建筑，每個模塊單元均在工廠進行內部墻板、屋面板、管線、管道安裝，完成安裝后運輸至施工現(xiàn)場，通過角件等節(jié)點連接構造進行連接裝配，主要受力體系為柱承重的鋼框架體系。由于模塊單元之間多采用角件連接，其連接為半剛性連接[2]，同時節(jié)點區(qū)域存在多梁多柱并存的問題。因此，普通框架計算模型簡化分析方法不能直接運用到疊箱式模塊化建筑的結構性能分析。

許多學者提出半剛性連接框架的有限元分析方法，通過分析節(jié)點柔性連接以及構件幾何非線性特性研究了半剛接的框架內力，但計算以及模型建立較為復雜。查曉雄等[3]通過有限元分析軟件ABAQUS對六層集裝箱模型進行數(shù)值模擬，推導了摩擦系數(shù)和阻尼比之間的關系，得到了各層的等效阻尼比。左洋等[4]基于蒙皮理論分析箱體側壁波紋板的剛度問題，進而推導出單個集裝箱的剛度，并且利用有限元軟件驗證了公式的正確性。CAO等[5]利用有限元軟件分析多層集裝箱結構在水平荷載作用下的穩(wěn)定性、位移變形能力以及內部構件的應力，對集裝箱結構提出利用加強帶固定的設計建議。

文章通過結構力學方法，以多層箱式模塊化建筑為例，在已知半剛性節(jié)點的初始轉動剛度前提下，分析了疊箱式模塊化建筑的簡化計算模型，推導其在豎向荷載和水平荷載作用下的簡化計算公式，并對比驗證了簡化計算模型與數(shù)值模擬結果。

1 疊箱式模塊化建筑豎向荷載作用下簡化計算方法

1.1 彎矩分配法在疊箱式模塊化建筑上的應用

目前，隨著有限元方法的迅速發(fā)展，對結構進行計算方法簡化研究具有重要意義，設計人員可以根據(jù)簡化計算結果對有限元模型的合理性進行驗證，并選擇合理的結構設計方案[6]。疊箱式模塊化建筑受到豎向荷載作用時的變形如圖1所示。

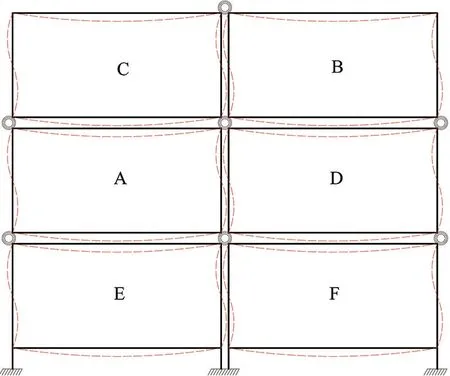
圖1 疊箱式模塊化建筑豎向荷載下變形圖

由于模塊單元之間半剛性節(jié)點的存在，相鄰模塊單元因發(fā)生變形而產生彎矩，普通框架彎矩分配法中將單個桿件視為基本構件的假定不再適用于疊箱式模塊化建筑。參考彎矩分配法計算框架結構在豎向荷載作用下內力的思路，采用平衡條件剖析法[7]，計算模塊單元內力時，對其余模塊單元內部梁柱節(jié)點附加剛臂約束，將疊箱式模塊化建筑每個模塊單元視為基本構件，分配彎矩，再將半剛性連接節(jié)點處的彎矩在模塊單元內部進行分配。

1.1.1 模塊單元固端彎矩

模塊單元豎向集中荷載作用下的計算簡圖如圖2所示，以集中荷載作用下的單個模塊單元為例，通過位移法可求解模塊單元A的固端彎矩[8]。由位移法計算模塊單元固端彎矩，其計算過程由式(1)～(4)表示為

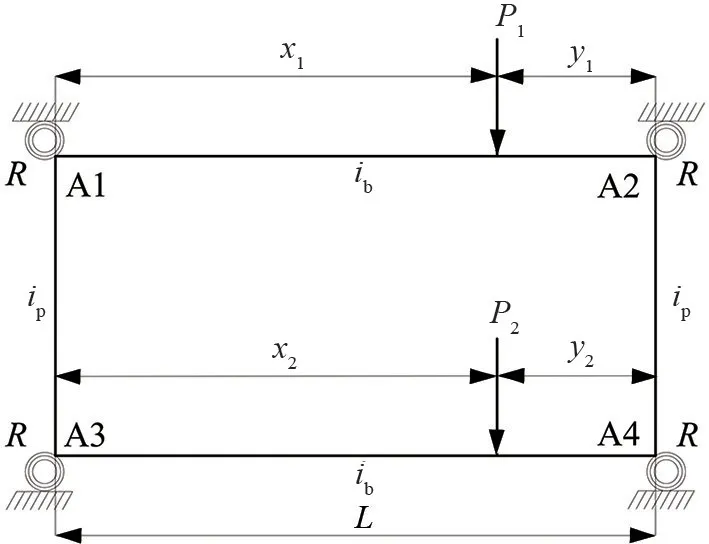
圖2 模塊單元豎向集中荷載作用下計算簡圖

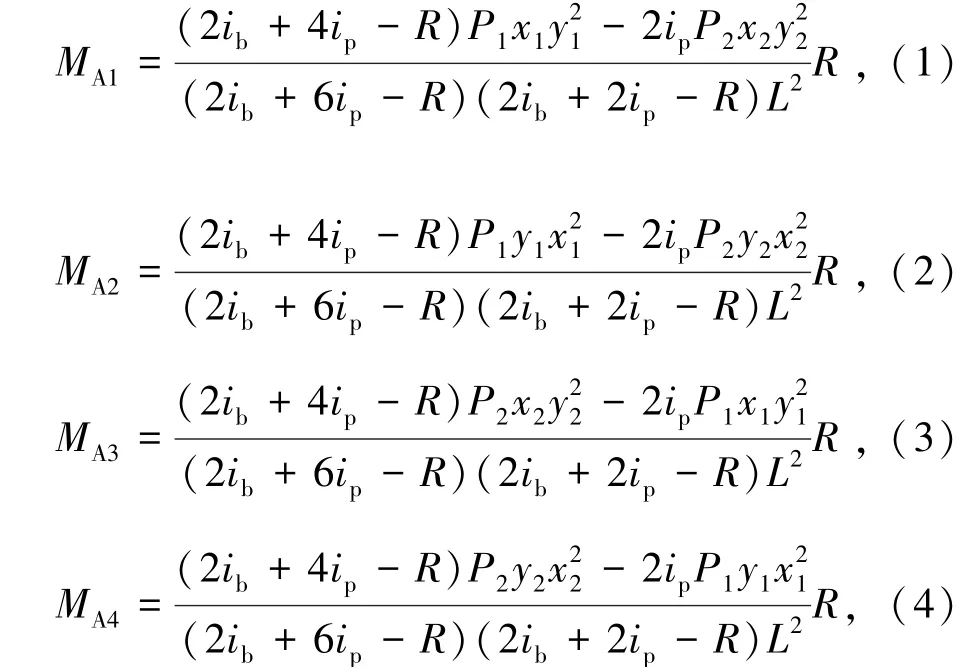
式中MA1、MA2、MA3、MA4分別為模塊單元節(jié)點A1、A2、A3、A4的固端彎矩，kN·m；P1、P2分別為作用在梁A1A2和梁A3A4的集中力，kN；R為半剛性節(jié)點的轉動剛度，(kN·m)/mrad；ib為模塊單元梁的線剛度，kN·m；ip為模塊單元柱的線剛度，kN·m。

簡化式(1)～(4)的計算結果，最終得到模塊單元固端彎矩的表達式，由式(5)～(8)表示為

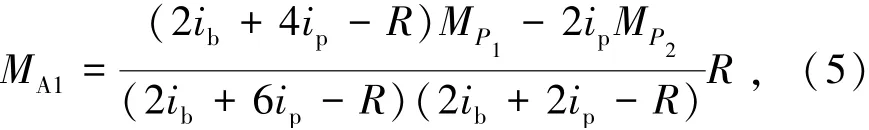
式(5)～(8)同樣適用于均布荷載及其他荷載作用下模塊單元固端彎矩的計算，只需將M P1、M′P1、M P2、M′P2換成相應荷載作用在兩端剛接梁的固端彎矩。

1.1.2 模塊單元的轉動剛度

計算模塊單元轉動剛度時，考慮了半剛性連接節(jié)點的影響，在模塊單元梁柱接觸處施加附加剛臂約束。模塊單元梁柱線剛度如圖3所示，R為半剛性節(jié)點初始轉動剛度；與半剛性連接框架相同，θAM(M＝1，2，3，4)為AM處假設節(jié)點為鉸接時節(jié)點轉角；θrAM(M＝1，2，3，4)為半剛性節(jié)點的節(jié)點轉角。

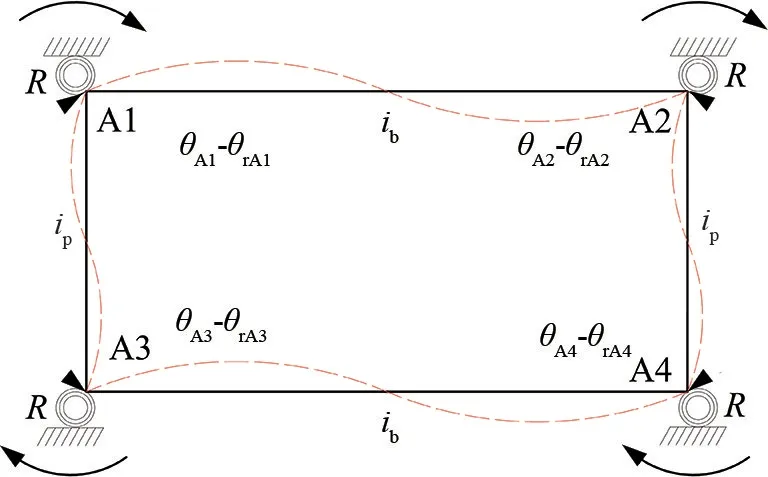
圖3 模塊單元添加剛臂約束計算簡圖

以A1節(jié)點為例，梁A1A2、柱A1A3的轉角位移方程由式(13)～(14)表示為

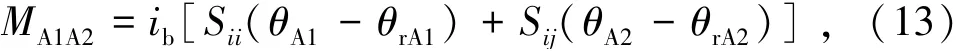
由于模塊單元梁的軸力很小，可以忽略不計，所以穩(wěn)定函數(shù)取值為S ii＝4、S ij＝2。

同理，可以得到模塊單元其他構件轉角位移方程。由A1、A2、A3、A4等4個節(jié)點彎矩平衡，得到4個節(jié)點彎矩平衡方程，由式(17)～(20)表示為

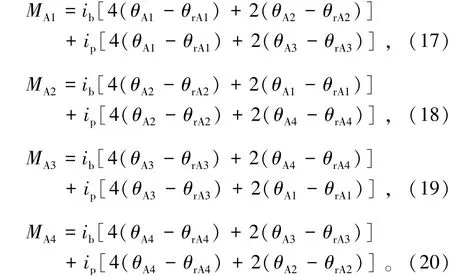
聯(lián)立(17)～(20)，根據(jù)轉動剛度的定義，轉動剛度矩陣由式(21)[10]表示為

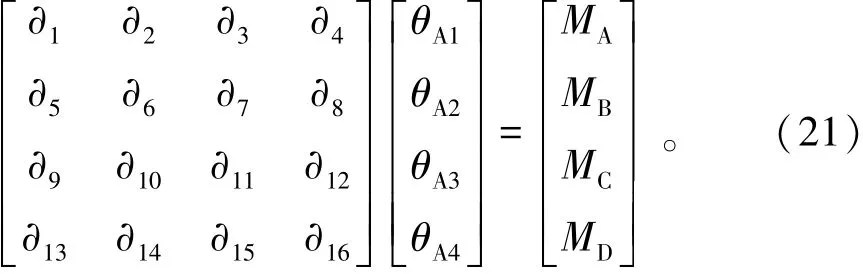
模塊單元在A1、A2、A3、A4點的轉動剛度分別為SA1＝?1、SA2＝?5、SA3＝?9、SA4＝?13，其中?M(M＝1，5，9，13)有且僅有梁柱線剛度和半剛性節(jié)點轉動剛度組成。

1.1.3 分配系數(shù)

疊箱式模塊化建筑結構計算簡圖如圖4所示，以模塊單元A、B、C、D公共節(jié)點處為例，模塊單元A在A2處分配系數(shù)μ可由式(22)[10]表示為

圖4 疊箱式模塊化建筑結構計算簡圖

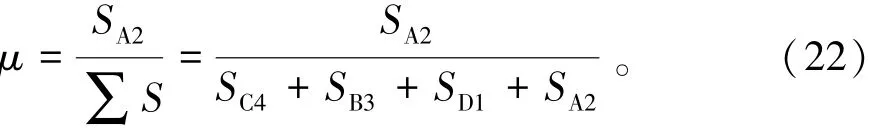
1.1.4 傳遞系數(shù)

以圖2中模塊單元A為例，節(jié)點A1的彎矩會向A2、A3、A4傳遞。傳遞系數(shù)可由式(23)～(25)[10]表示為

1.2 基于分層法的計算模型簡化

對分析疊箱式模塊化建筑采用的分層法做如下假定:(1)在豎向荷載的作用下，疊箱式模塊化建筑的側移可以忽略不計，用彎矩分配法計算；(2)每層模塊單元梁上的豎向荷載對其他層的模塊單元梁及非相鄰模單元柱的內力影響忽略不計，把多層模塊化建筑分成一層一層單獨計算。采用分層法計算每層疊箱式模塊內力時，可只考慮該層疊箱式模塊，在同層模塊之間進行力矩分配即可。由上述假定，多層疊箱式模塊化結構在豎向荷載作用下可分層計算。

1.3 算例1

采用彎矩分配法求解模塊單元內力，由于模塊單元層之間節(jié)點處的連接方式一致，模塊建筑整體進行了規(guī)則化設計，模塊單元之間的傳力方式相同，內力值的大小僅由固端彎矩、轉動剛度、彎矩分配系數(shù)、彎矩傳遞系數(shù)決定。對雙層模塊單元的內力傳遞方式及簡化計算方法進行研究，計算簡圖如圖5所示，模塊單元梁、柱幾何性質為Ib＝2.31×10－4m4、Ic＝4.77×10－5m4、轉動剛度R＝39.60(kN·m)/mrad。

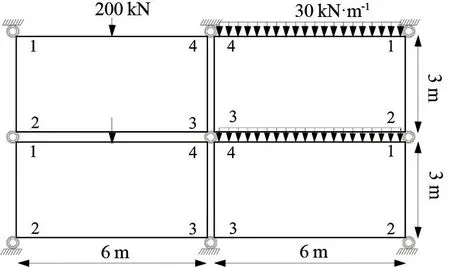
圖5 雙層模塊單元計算簡圖

根據(jù)《歐洲規(guī)范3:鋼結構設計 第1.1部分:一般規(guī)則和建筑物規(guī)則》(Eurocode 3:Design of steel structures-Part 1.1: General rules and rules for buildings，EC3:1.1)[11]，半剛性節(jié)點在彈性階段內的連接剛度進行二分之一折減，則計算時所采用的連接剛度Rk＝R/2＝19.8(kN·m)/mrad。通過式(5)～(8)計算一層模型固端彎矩，根據(jù)轉動剛度的剛度矩陣即式(21)計算轉動剛度，進而得到彎矩分配系數(shù)和彎矩傳遞系數(shù)，整理計算模型彎矩計算系數(shù)見表1，表中WL和WR分別代表左側節(jié)點和右側節(jié)點。根據(jù)分層法的假定，把多層模塊化建筑分成獨立層單獨計算，基于結構力學基本理論計算獨立層梁柱彎矩，然后疊加兩層柱端彎矩，最終彎矩分布如圖6所示。

表1 彎矩計算系數(shù)表

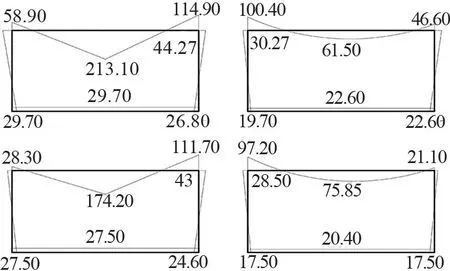
圖6 內力簡化計算結果圖/(kN·m)

利用通用結構分析與設計軟件Midas Gen建立有限元分析模型，對算例中的模塊單元進行數(shù)值模擬計算[12]。在有限元模型中，疊箱式模塊化建筑的梁與柱均采用一般梁單元進行模擬。該單元使用一般的三維梁－柱公式，能夠考慮包括雙軸彎曲、扭轉、軸向變形、雙軸剪切變形等效應；模塊單元之間采用彈簧單元模擬連接節(jié)點，該彈簧能夠約束相鄰模塊單元的平動位移并具有相應的轉動剛度和轉動能力。模塊單元的彎矩內力數(shù)值模擬結果如圖7所示。

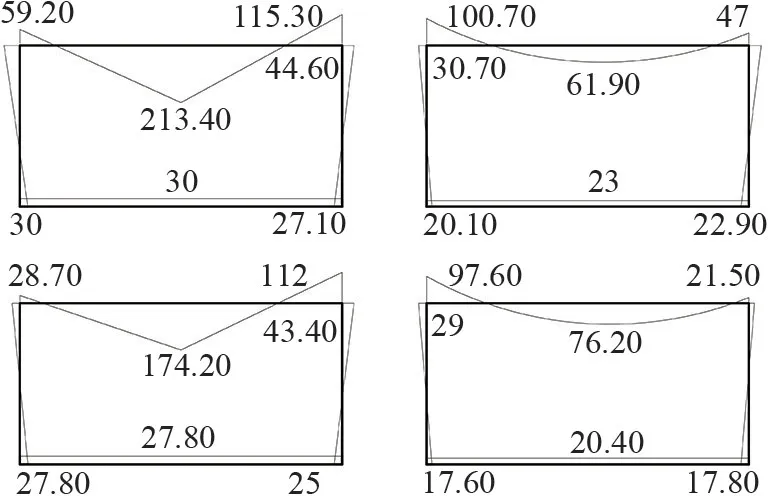
圖7 基于Midas Gen的數(shù)值模擬結果圖/(kN·m)

通過對比彎矩內力簡化計算結果(如圖6所示)和數(shù)值模擬結果(如圖7所示)可發(fā)現(xiàn)，構件的彎矩內力簡化計算結果和數(shù)值模擬結果較吻合，誤差很小，說明采用簡化計算方法與有限元數(shù)值模擬方法對模塊單元進行彎矩內力計算的結果一致性較高，簡化計算方式較合理。

2 疊箱式模塊化建筑水平荷載作用下簡化計算方法

2.1 D值法在疊箱式模塊化建筑上的應用

計算結構的位移時需要計算結構抗側剛度[13]，疊箱式模塊化建筑柱子的抗側剛度及反彎點位置與模塊單元柱兩端轉角有關[14]。對比普通框架D值法推導疊箱式模塊化建筑柱抗側剛度D，做以下假定:(1)水平荷載作用下模塊內單元梁柱節(jié)點與相臨的模塊單元節(jié)點轉角相同。(2)水平荷載作用下上下模塊單元柱的弦轉角及線剛度相同。根據(jù)以上兩個假定，可以將模塊單元之間的半剛性連接節(jié)點簡化為鉸接節(jié)點如圖8所示。通過對D值和反彎點的修正，可求出疊箱式模塊化建筑在水平荷載作用下的層間位移和內力。

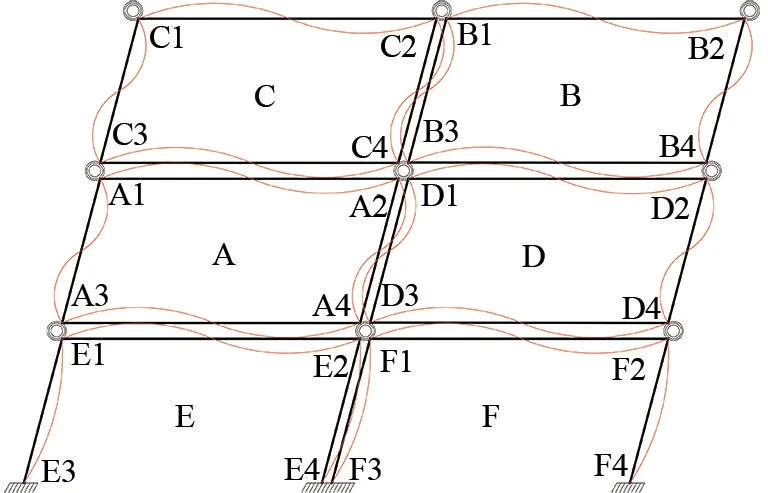
圖8 疊箱式模塊化建筑水平荷載作用下變形圖

2.1.1 一般層模塊單元柱抗側剛度修正

以一般層模塊單元A為例，如圖9所示，其梁柱轉角位移方程由式(26)和(27)[10]表示為

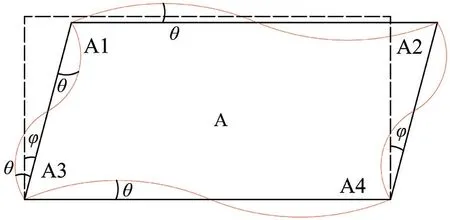
圖9 一般層模塊單元水平荷載作用下變形圖

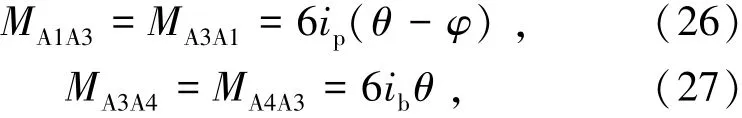
式中θ為節(jié)點轉角；φ為柱弦轉角，φ由式(28)表示為

式中Δ為柱側移，m；h為柱高度，m。

若使節(jié)點A1、A3力矩平衡，則應滿足的條件由式(29)和(30)表示為

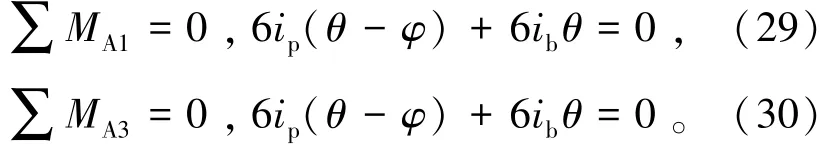
由此推導模塊單元梁柱線剛度比，由式(31)和(32)表示為

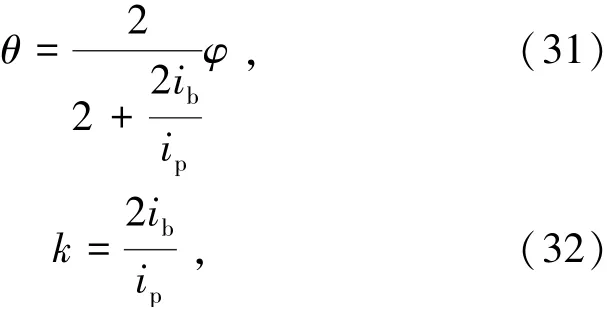
式中k為梁柱線剛度比。

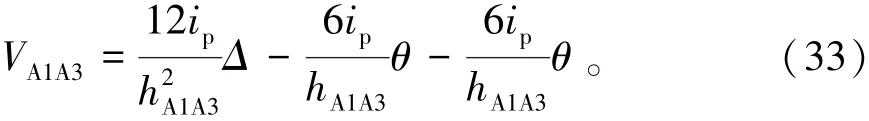
聯(lián)立(28)～(33)得

式中α為抗側剛度修正系數(shù)，

當Δ＝1時，就是考慮兩端有轉角的側移剛度DA1A3，由式(35)表示為

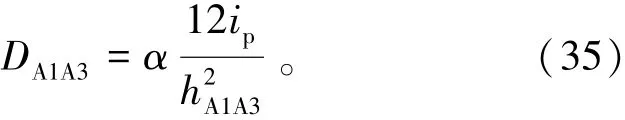
2.1.2 底層模塊單元柱抗側剛度修正

以底層模塊單元E為例，如圖10所示，其梁柱轉角位移方程由式(36)和(37)表示為[10]

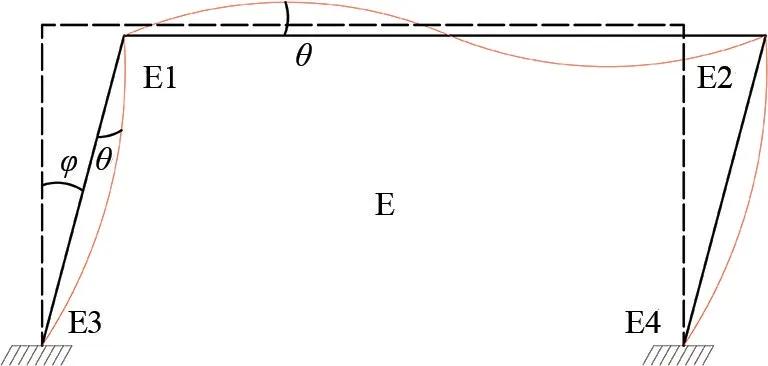
圖10 底層模塊單元水平荷載作用下變形圖

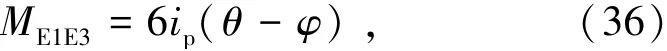
若使節(jié)點E1力矩平衡，由式(38)表示為

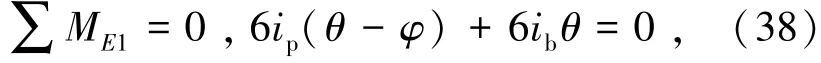
則

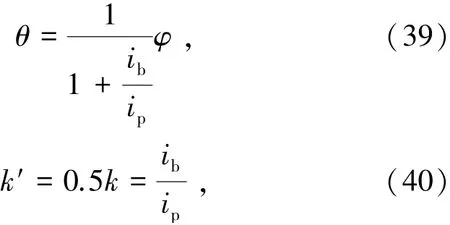
式中k′為底層梁柱線剛度比。

模塊單元柱剪力VE1E3由式(41)表示為

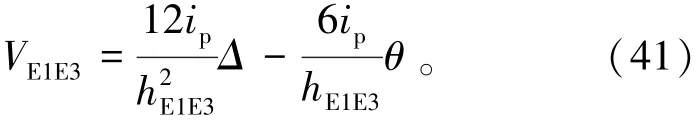
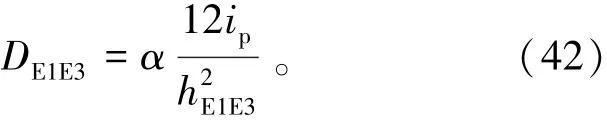
2.1.3 疊箱式模塊化建筑的反彎點高度

一般框架結構梁的線剛度和層高會有所變化，影響其柱反彎點高度[15]。對于疊箱式模塊化建筑，模塊單元在工廠中加工預制工業(yè)化程度極高[16]。在同一建筑中模塊單元的橫梁線剛度不變，層高保持固定的模數(shù)，所以為了方便簡化模塊化結構的計算，可認為疊箱式模塊化建筑中上、下模塊單元柱端轉角相同，即反彎點位于模塊單元柱的中點。

2.1.4 疊箱式模塊化建筑側移計算

水平荷載作用下的普通框架結構變形包括總體剪切變形和總體彎曲變形[17]。對于疊箱式模塊化建筑，除以上兩種變形外，還包括模塊單元節(jié)點連接處的水平滑動變形。由于節(jié)點連接處的角件和連接板均為工廠預制，現(xiàn)場進行可靠連接安裝時，具有較大的抗剪剛度，故節(jié)點連接處的水平滑動變形可以忽略。因此，疊箱式模塊化建筑的側移計算與普通框架一致，只需用式(35)～(43)替換普通框架的D值即可。

2.2 算例2

根據(jù)D值法對3層兩跨疊箱式模塊化建筑的側向位移進行分析計算，計算簡圖如圖11所示，模塊單元的梁、柱相關的幾何性質有:Ib＝2.31×10－4m4、Ic＝4.77×10－5m4、轉動剛度R＝39.60(kN·m)/mrad。

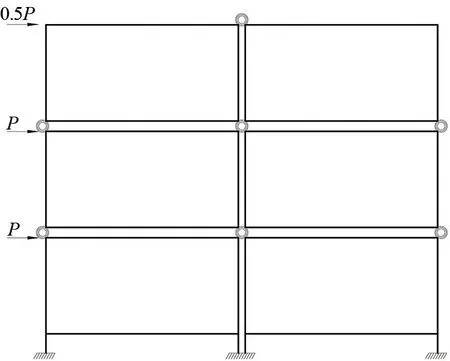
圖11 計算簡圖

依據(jù)EC3:1.1[11]建議，半剛性節(jié)點在彈性階段內的連接剛度進行二分之一折減，則計算時所采用的連接剛度Rk＝R/2＝19.8(kN·m)/mrad。按照2.1.1和2.1.2中給出的計算方法，整理模塊單元柱的抗側剛度修正系數(shù):一般層的層邊柱修正系數(shù)α1＝0.3；一般層的層中柱修正系數(shù)α2＝0.3；底層邊柱修正系數(shù)α3＝0.2；底層中柱修正系數(shù)α4＝0.2。

整理D值法計算結果和數(shù)值模擬結果見表2，兩者計算結果較為接近，說明文章提出的修正反彎點法能夠精確地計算疊箱式模塊化建筑結構在水平荷載下的側移。理論計算結果小于數(shù)值模擬結果的原因則是由理論計算過程中忽略梁的軸向剛度造成的。

表2 水平荷載作用下位移表

3 結論

根據(jù)上述研究可以得出以下結論:

(1)提出了適用于疊箱式模塊化建筑在豎向荷載下的計算模型及簡化計算方法，該簡化方法與有限元分析結果吻合度較高，可用于疊箱式模塊化建筑初步設計與最終校核。

(2)建立了疊箱式模塊化建筑的抗側剛度計算方法，發(fā)現(xiàn)其公式形式與普通框架抗側剛度計算公式較相似，修正了底層模塊單元柱的抗側剛度，確定了疊箱式模塊化建筑模塊單元柱的反彎點高度位于中點。

(3)計算疊箱式模塊化建筑結構側移時模塊單元之間的半剛性連接節(jié)點可簡化為鉸接連接節(jié)點，簡化計算方法與有限元數(shù)值分析結果吻合較好。