黃土高原坡度因子的多重分形譜特征

夏積德, 叢佩娟, 李俊鋒

(1.楊凌職業技術學院, 陜西 楊凌 712100; 2.水利部 水土保持監測中心, 北京 100053; 3.陜西測繪地理信息局, 陜西 西安 710054)

地形因子是水土流失、水文過程模擬的參數，科學量化地形因子對于水土流失這一地理界面過程的研究具有極為重要的意義。大量研究發現，自然界中大部分區域的地表形態復雜多變，呈現出明顯的不均勻性和分形特征，即具有以非整數維形式充填空間的形態特征。若僅采用普通分形維數的方法并不能詳細且全面地反映不同區域條件、不同尺度下的地形因子特征。在多重分形理論被提出后，由于其采用廣義維數和多重分形譜來描述分形客體，考慮了對象屬性在幾何支集的空間奇異性分布這一特點[1]，即能考慮到復雜分形體內部不同區域呈現出不同分形特征，因而逐漸被用于包括地形地貌學在內的各種地理學相關研究。沈中原等[2]借助多重分形理論構建了海拔信息空間分布概率計算模型；張建興等[3]探討了黃土高原若干流域的河網分形特征并基于此建立起產沙模數模型；王民等[4-5]運用多重分形理論及其實現方法分析了大理河流域地表形態的多重分形特征。這些研究多運用分形理論表征區域地貌形態的綜合特征[6]，但對于黃土高原地區地形因子(如坡度)的多重分形研究還很少涉及。因此，本文運用多重分形理論來研究黃土高原地區地形因子的特點，旨在為黃土高原地區開展地形因子方面的研究提供參考。本研究對區域水文過程、水土流失預報模型的建立具有積極意義。

1 研究區概況

黃土高原地處中國中北部地區，轄內蒙古、山西、陜西、寧夏、甘肅、青海、河南7個省區，東西跨越1 000 km多，南北跨越近750 km，總面積約為6.40×104km2，海拔高度介于1 000～3 000 m，是中國4大高原之一。黃土高原整體表現出西北高東南低的特點，寧夏西南方的六盤山和山西西部的呂梁山將整個黃土高原劃分為3個部分，在此劃分基礎上進一步按照地形地貌特點將黃土高原劃分為山地區、黃土丘陵區、黃土塬區以及河谷平原區4種類型。山地區主要包括馬銜山地區、拉脊山地區、六盤山地區、子午嶺地區、太行山地區和呂梁山地區，海拔跨度大、地形地貌差異較大，由于長期受重力、流水以及風力等侵蝕因素的影響，山地區的地貌侵蝕現象嚴重，溝壑明顯，坡度較大；丘陵區作為黃土高原地區較為典型的地形地貌區域有著十分廣闊的分布區域，其占據了超過黃土高原地區一半的面積。丘陵區在黃土高原分布范圍遼闊，不同區域的丘陵區之間還存在不小的差異；黃土塬區中分布著大量塬面，塬面頂部十分平坦，地形復雜程度較低。與之形成強烈對比的是塬面周圍陡峭的溝壑，這些溝壑分布在一個又一個塬面之間，使得黃土塬區內部的地形地貌形成了十分大的反差，地形復雜度對比強烈；河谷平原區以關中平原最具代表性，關中平原位于陜西省中部，呈東西帶狀分布，地形較為單一，多為平原，在長期的沖擊下形成了平坦開闊的地貌景觀。

2 研究方法

在黃土高原不同地貌類型區內選擇合適的研究區，獲取各子研究區的DEM(來源于地理空間數據云(http:∥www.gscloud.cn/，空間分辨率為30 m×30 m，并在GIS中提取得到坡度因子的柵格數據；隨后，采用盒維數的計算方法，計算得到坡度因子的多重分形譜并對其主要參數及圖像特征進行對比分析。

2.1 多重分形譜的計算

盒維數方法是一種基于統計學原理的計算多重分形的方法，具有簡便且易于理解的特點，經常被用于地形地貌多重分形的計算[7]。盒維數是用一系列緊密相連的正方形盒子去覆蓋分形體，即將研究對象分為很多個(假設有i行j列總計N個)尺度大小為r的正方形網格單元[8]，然后計算每個網格單元內的概率測度。對于坡度因子來說，概率測度的大小可以用坡度概率函數表示，每個小網格單元的坡度概率函數的計算公式為：

(1)

式中：Pij(r) 表示位于第i行第j列的網格的坡度概率函數;Air(r)表示位于第i行第j列的網格內的坡度統計值;N表示網格單元的總個數,其在數值上滿足:N=i×j。

根據公式(1)并結合多重分形理論[9-10]可知，坡度概率函數可以粗略衡量一個網格單元區域的地形特點，數值越小表示該網格區域內坡度越小，具有越平坦的地形特點，如塬面、平原等；反之，坡度概率函數的數值越大表示網格區域內的坡度越大，地形起伏程度越大，如峁、坡面等。

在盒維數方法中，檢驗一個研究對象是否具有多重分形特征，有一個配分函數的概念[11]，配分函數的計算公式如下：

(2)

式中：Xq(r)表示分形體的配分函數;Pij(r)表示位于第i行第j列的網格的坡度概率函數;q表示階矩,可以取任意實數,配分函數中q的取值直接影響著不同的概率測度在整個配分函數上所占比重的大小。

對于給定的一對r和q，都可以通過公式(1)和公式(2)計算得到一個配分函數。在盒維數方法中，如果研究對象具有多重分形特征，那么配分函數Xq(r)和r之間應該滿足以下的關系[12]：

Xq(r)∝rτ(q)

(3)

式中：τ(q)是關于q的一個表達式,在探討研究對象是否具有多重分形特征的過程中無關緊要。

根據上述關系可知，對兩邊同時取對數，lnXq(r)和lnr滿足線性關系。因此繪制以lnr為橫軸，lnXq(r)為縱軸的散點分布圖，對其擬合，如果lnXq(r)—lnr圖像為一系列斜率不等的直線，則表明研究對象具有多重分形特征[13]，可以進一步計算其多重分形譜及其特征參數。

本研究利用Chhabra等[14]提出的一種建立在盒維數方法基礎上的通過擬合參數計算多重分形譜的方法來計算多重分形譜。這種方法需要設立一個經過歸一化處理的測度集μij(q,r)，其計算公式如下：

(4)

在這個測度集的基礎上結合多重分形的概念，可以通過下面的公式來計算多重分形中的奇異指數α和分形維數f(α)：

(5)

(6)

奇異指數α是一個標度指數，它是反映分形體內各個小區間的奇異程度的一個量，α的數值與其所在的位置有關。將分形上具有相同α值的小區間數記為f(α)，基于此可以得到α—f(α)的函數圖像，稱為奇異譜。橫坐標的范圍是多重分形譜奇異指數α的分布范圍，α的大小反映該部分的奇異程度。

在計算時，常常按照公式(5)和公式(6)的數學幾何意義借助擬合的方法來得到α和f(α)的值。將公式(5)處理可得：

(7)

公式(7)根據一次函數相關概念及其圖像性質可知α為∑μij(q,r)·lnPij(r)—lnr圖像的斜率，類似地，f(α)為∑〔μij(q,r)·lnμij(q,r)〕—lnr圖像的斜率。

首先確定一個q值，保持階矩q不變而改變尺度r，每選取一個r進行計算，按照公式(1)，(2)，(4)就可以得到一個對應的∑μij(q,r)·lnPij(r)—lnr和∑〔μij(q,r)·lnμij(q,r)〕，通過在二維坐標系中進行擬合便可得到每個q對應的奇異指數α和分形維數f(α)。改變階矩q的值，便能得到一系列的α和f(α)，而多重分形譜就是以α為橫坐標，f(α)為縱坐標的圖像。

2.2 特征參數的取值

(1) 格網大小(尺度)r的選取。根據多重分形理論，格網的大小直接影響到格網的總數量和每個格網的概率測度，這兩個因素決定著多重分形計算過程中的效率和準確性，因此從簡便、可實施的角度出發，需選取大小為30 m整數倍的格網來覆蓋研究區。結合所選4個研究區坡度數據的實際情況，規定一個柵格大小即30 m為一個單位，通過反復試驗最終選取格網尺度大小為20，30， 40，…，190，200個單位，亦即600，900，1 200，…，5 700，6 000 m，共19種。

(2) 階距q取值范圍的確定。公式(3)配分函數中q的取值直接影響著不同的概率測度在整個配分函數上所占比重的大小[15]，當q取正值且取值越大，配分函數越能反映具有較大坡度概率函數的那些網格單元的特征和性質；當q取負值且取值越小，則配分函數越能反映具有較小坡度概率函數的那些網格單元的特征和性質。因而q的取值對配分函數的計算結果影響很大，不同區域坡度的位置分布和大小范圍不同，各研究區q的取值范圍也不同，研究表明，在地形地貌多重分形的計算中，q值分布在0左右且通常介于±30之間[4]。

本研究對每一個子研究區在-50～50之間等間距選取不同的q值，通過盒維數計算多重分形譜的方法驗證q是否在合適的區間。在初步確定q的合適區間后繼續加密q的取值，最終得到每個研究區階矩q的最佳取值范圍見表1。

表1 研究區q最佳取值范圍

3 結果與分析

3.1 坡度概率分布特點

為更詳細、系統地了解各研究區坡度大小的分布情況，對4個研究區的坡度進行統計(圖1)。可以看出，山地區、黃土丘陵區、黃土塬區、河谷平原區的坡度介于0°～10°之間的柵格占比分別為35.80%，35.50%，60.75%，>99.99%；介于10°～20°之間的柵格占比分別為24.23%，40.59%，16.94%，<0.01%；介于20°～30°之間的柵格占比分別為20.48%，20.92%，13.74%，0%；介于30°～40°之間的柵格占比分別為15.76%，2.89%，7.54%，0%；介于40°～50°之間的柵格占比分別為3.63%，0.10%，1.02%，0%；介于50°～60°之間的柵格占比分別為0.1%，0%，0.01%，0%。

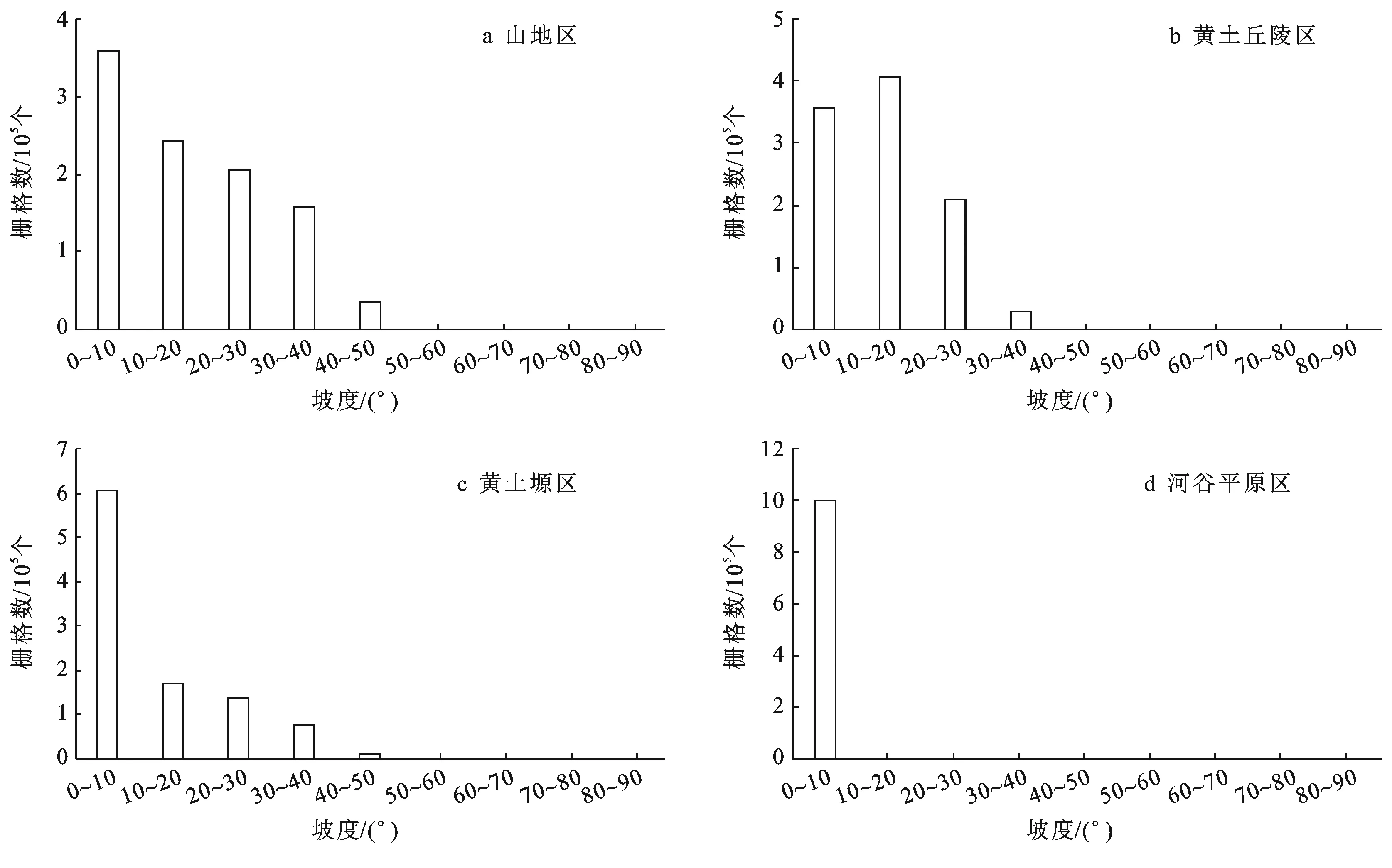
圖1 研究區不同地形坡度統計

由統計結果得知：①山地區的坡度分布區間最大，大部分柵格處于0°～20°這一中小坡度區間，坡度大于40°的區間在4個研究區中占比最高；②黃土丘陵區坡度介于0°～10°區間內的占比最少，坡度大部分位于10°～20°這一坡度范圍內。同時，大于30°的坡度占比較小，因此在黃土丘陵研究區內大坡度的地形較少，地形特點較為均一；③黃土塬區有大面積的平坦塬面，坡度大部分介于0°～10°之間，因此坡度值往往很小，由于所選研究區面積固定為30 km×30 km，在這樣一個較大的范圍內不可避免地包括了塬面周圍的切溝、坡面等非塬面地形，因此也存在少量坡度大于20°的非塬面特征柵格；④河谷平原區的坡度統計圖特征十分明顯，幾乎所有柵格的坡度均介于0°～10°之間，在4個研究區中地形最為平坦。

3.2 多重分形特征檢驗結果

在計算坡度信息多重分形譜前需要先驗證研究對象是否具有多重分形特征。為此，在平面坐標系中，以lnr為橫坐標，lnXq(r)為縱坐標，繪制出每個研究區的lnXq(r)曲線，4個研究區坡度地形因子繪制的lnXq(r)—lnr曲線見圖2。

從圖2中可以看出，每個研究區在各自合適的q范圍內，當尺度對數滿足3.0≤lnr≤5.3時，配分函數對數與尺度對數之間存在很好的線性關系，表明黃土高原區域上述4個研究區的坡度信息具有明顯的多重分形特征，可以進行多重分形譜的計算。

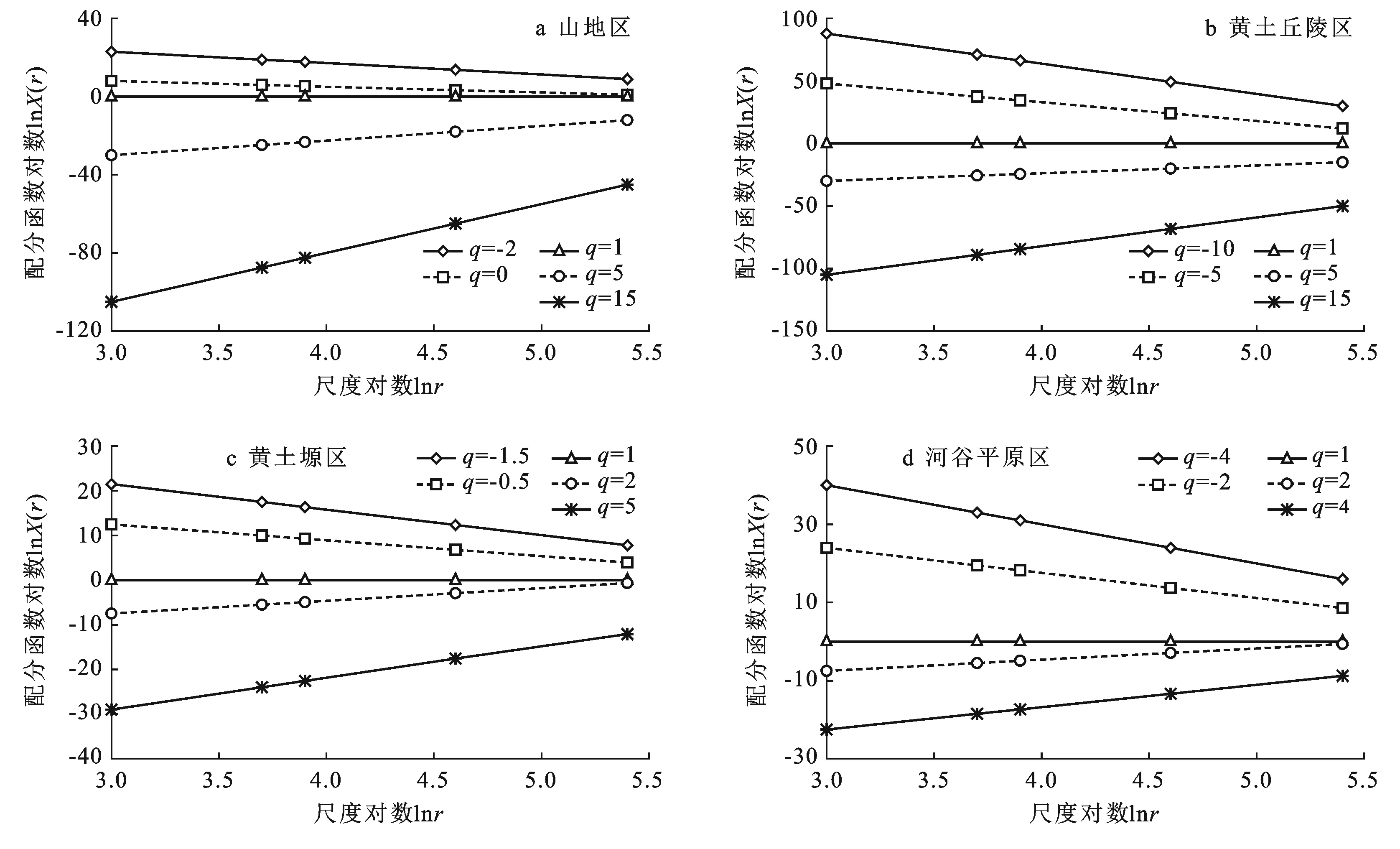
圖2 研究區不同地形lnXq(r)-lnr特征

3.3 坡度信息多重分形譜及其參數

以坡度數據為基礎，利用多重分形理論原理和計算方法得到研究區坡度信息多重分形譜散點分布圖(圖3)及其參數結果(表2)。由圖3的多重分形譜可以看出，不同研究區的多重分形譜均為凸函數。在一個研究區內，多重分形譜函數值隨著坡度奇異指數的增加均呈現出先遞增后遞減的變化特征。而在各研究區之間，坡度多重分形譜的對稱性、圖像分布范圍均有不同，這是由于各研究區多重分形譜參數的差異導致的。通過對多重分形譜圖的二維坐標系進行擬合，得到各研究區詳細的多重分形譜參數信息見表2。

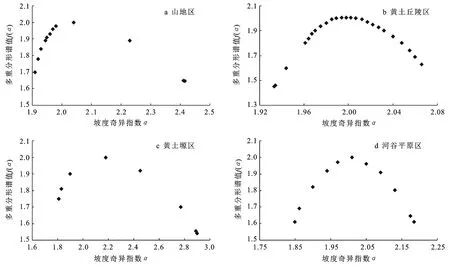
圖3 研究區不同地形多重分形譜特征

表2 研究區多重分形特征參數

從多重分形譜參數統計表中可以看出，最小坡度奇異指數的最大值為1.94，出現在黃土丘陵區，最小值為1.82，出現在黃土塬區，說明在4個研究區中，坡度最大的地貌單元出現在黃土塬區(奇異指數最小值對應的是坡度最大地貌單元的性質)；最小坡度奇異指數相應的多重分形譜值的最大值為1.78，出現在黃土塬區，最小值為1.45，出現在黃土丘陵區，這說明最小坡度奇異指數對應的地貌類型單元在黃土塬區所占比例最大，這與魯克新等[16]的研究結果相一致，在黃土丘陵區所占比例最小，即坡度最大的子區域在黃土塬區占比最高，而在黃土丘陵區占比最低；最大坡度奇異指數的最大值為2.90，出現在黃土塬區，最小值為2.07，出現在黃土丘陵區，說明地形特征最簡單的地貌單元出現在黃土塬區；最大坡度奇異指數所對應的多重分形譜值最大值為1.63，出現在河谷平原區，最小值為1.56，出現在黃土塬區，說明最大坡度奇異指數對應的地貌類型單元在河谷平原區所占比例最大，在黃土塬區所占比例最小。黃土塬區對應的坡度奇異指數的極值最大，為1.08，山地區次之，為0.50，然后是河谷平原區的0.35，而黃土丘陵區為0.13。

在多重分形譜左端點值與右端點值之差這個參數上，從絕對值的大小來看，黃土塬區最大，數值為0.22，說明該研究區最小坡度奇異指數對應的地貌單元所占比例與最大坡度奇異指數對應的地貌單元所占比例的差異性最大，黃土丘陵區次之，差異性最小的是河谷平原區。從正負的角度來看，黃土丘陵區和河谷平原區為負值，山地區、黃土塬區為正值，說明前兩個研究區的大坡度地貌單元所占比重較后兩個研究區要小。

4 討論與結論

目前，已有大量研究者采用簡單分形維數、多重分形譜和聯合多重分形等方法來表征復雜地貌的形態及其特征[17]，但對于坡度因子的多重分形研究還很少涉及。本研究在DEM數據的基礎上，將黃土高原按照不同地形地貌劃分為山地區、黃土丘陵區、黃土塬區、河谷平原區，并對坡度因子的多重分形譜圖像和多重分形特征參數進行了對比分析，總結出各自區域的多重分形譜特點，為后續開展黃土高原地形因子方面的研究打下了基礎，對區域水文過程、水土流失預報模型的建立具有積極意義。

像元尺度的選取是地形因子分形維數計算的關鍵，像元尺度在范圍之外時，地形因子的分形計算沒有意義。本研究對研究區的多重分形特征進行驗證，結果表明尺度對數滿足3.0≤lnr≤5.3時，黃土高原地區坡度地形因子的配分函數對數與尺度對數之間的線性關系良好，表明黃土高原區域上述4個研究區的坡度信息具有明顯的多重分形特征，可以進行多重分形譜的計算。

不同地形的多重分形譜圖以及特征參數都有著明顯的差異，其橫坐標奇異指數α的大小反映該區域的奇異程度，這一參數的數值越大，表明分形體坡度特征的分異現象越大，其內部越不均勻、越復雜，兩極化趨勢越明顯，α最小值、最大值所對應的多重分形譜值記為f(αmin)，f(αmax)，描述了小坡度單元區域和大坡度單元區域在整個研究區域內所占的比例高低。通過多重分形譜的研究可以發現，最小坡度奇異指數的最小值為1.82，相應的多重分形譜值的最大值為1.78，最大坡度奇異指數在4個研究區內最大，所對應的多重分形譜在4個研究區最小為1.57，說明坡度最小地貌單元在黃土塬區所占比例最小，坡度最大的地貌單元出現在黃土塬區且占比最高。黃土丘陵區、河谷平原區則表現出較小的奇異指數變化范圍，黃土丘陵區最小坡度奇異指數的最小值為1.94，最大值為2.07，河谷平原區最小坡度奇異指數的最小值為1.85，最大值為2.19，相比之下地形較為均一。

通過多重分形譜與統計直方圖對照研究可以發現，在4個研究區中，黃土塬區有不少坡度達到了40°，且坡度最大的地貌單元出現在黃土塬區且占比最高，在地勢平坦的塬面出現這種情況是由于所選研究區面積固定為30 km×30 km，而單個塬面通常面積有限，在這樣一個較大且規則的范圍內不可避免地包括了塬面周圍的切溝、坡面等非塬面地形，因此其坡度統計中也存在少量坡度大于20°的非塬面特征柵格，這也是黃土塬區的多重分形譜中奇異指數最小、對應的多重分形譜值在4個研究區中最大的原因，同時也反映了研究區地形復雜的特點。結合多重分形理論的相關知識發現，本研究結果與實際情況有著較好的對應，表明基于多重分形理論與方法對黃土高原地區的地形因子進行量化研究是可行的，為黃土高原地區開展地形因子方面的研究提供了參考，對區域水文過程模擬、水土流失預報模型的建立具有積極意義。可為黃土高原的地貌學研究、土壤侵蝕研究和水土保持規劃工作的開展提供技術支持和幫助。