機(jī)械振源數(shù)估計(jì)的四線性平行因子方法研究

李志農(nóng) 朱亞靜 王冬

摘要： 針對(duì)三線性平行因子模型在機(jī)械振源數(shù)盲估計(jì)方法中存在的不足，即由于維度的限制只能對(duì)振動(dòng)信號(hào)的部分信息建模，信號(hào)中的時(shí)間序列信息被忽略。將三線性平行因子的機(jī)械振源數(shù)估計(jì)方法擴(kuò)展至四維，提出一種基于四線性平行因子的機(jī)械振源數(shù)估計(jì)方法。所提出的方法中，在三維的基礎(chǔ)上增加了第四個(gè)維度（時(shí)間維），利用四線性交替最小二乘法迭代更新載荷矩陣，用核一致診斷法估計(jì)振源數(shù)。提出的方法既繼承了三線性平行因子的獨(dú)特優(yōu)勢(shì)，同時(shí)，又包含了更完整的振動(dòng)信號(hào)的信息。相比三線性平行因子機(jī)械振源數(shù)估計(jì)方法，同組分?jǐn)?shù)條件下四線性平行因子比三線性平行因子得到的核一致值更高，估計(jì)更加準(zhǔn)確。仿真結(jié)果表明，提出的方法優(yōu)于三線性平行因子機(jī)械振源數(shù)估計(jì)方法。實(shí)驗(yàn)結(jié)果進(jìn)一步驗(yàn)證了提出的方法的有效性。

關(guān)鍵詞： 故障診斷; 四線性平行因子; 盲源分離; 機(jī)械振源數(shù)估計(jì); 四線性交替最小二乘

中圖分類號(hào)： TH165+.3; TN911.7? ? 文獻(xiàn)標(biāo)志碼： A? ? 文章編號(hào)： 1004-4523（2021）03-0619-07

DOI：10.16385/j.cnki.issn.1004-4523.2021.03.020

引? 言

傳統(tǒng)的機(jī)械故障源盲分離往往假設(shè)信號(hào)源數(shù)是已知的，例如，文獻(xiàn)[1]提出的旋轉(zhuǎn)機(jī)械監(jiān)測(cè)預(yù)處理盲分離方法和文獻(xiàn)[2]提出的用于殼體結(jié)構(gòu)振源數(shù)目估計(jì)的獨(dú)立分量分析方法，這些方法都是在信號(hào)源數(shù)已知的條件下進(jìn)行盲分離。然而，在實(shí)際工程中，機(jī)械故障源數(shù)往往是未知的，為此，需要探討關(guān)于源數(shù)未知條件下的機(jī)械故障盲分離方法。目前，基于源數(shù)估計(jì)的機(jī)械故障源盲分離方法取得了一些進(jìn)展[3?6]，例如，文獻(xiàn)[3]結(jié)合分?jǐn)?shù)傅里葉變換和盲分離理論的思想提出了一種機(jī)械故障源分離方法。文獻(xiàn)[4]基于小波包分析思想提出了一種機(jī)械振動(dòng)源數(shù)估計(jì)方法。然而，這些機(jī)械故障源數(shù)盲估計(jì)算法都屬于二維數(shù)據(jù)處理方法，采用矩陣分解，并附加了一些約束條件。一般來說，矩陣分解不是唯一的，除非施加約束性條件，如正交性、Toeplitz和恒模特性等。但實(shí)際應(yīng)用中并不能滿足這些苛刻的約束條件，所以需要尋求新的方法解決這一問題。

近年來，平行因子模型（PARAFAC）[7?8]因具有分解唯一性的優(yōu)勢(shì)備受關(guān)注，它起源于平行比例分布原則，因其優(yōu)勢(shì)，平行因子理論在許多領(lǐng)域得到快速發(fā)展，例如化學(xué)分析領(lǐng)域[9]、無線通信領(lǐng)域[10]、環(huán)境化學(xué)計(jì)量領(lǐng)域[11]、故障診斷領(lǐng)域[12]。特別在信號(hào)處理和故障診斷領(lǐng)域內(nèi)平行因子模型現(xiàn)已成為一種新型的、有力的研究手段。例如文獻(xiàn)[13]將平行因子理論應(yīng)用到陣列多參數(shù)的聯(lián)合估計(jì)中。文獻(xiàn)[14]將三維平行因子應(yīng)用到機(jī)械振源數(shù)估計(jì)之中，該方法可有效估計(jì)機(jī)械振源數(shù)目。但是實(shí)際的應(yīng)用中，使用現(xiàn)有的三維平行因子進(jìn)行機(jī)械振源數(shù)估計(jì)時(shí)，只能對(duì)采集信號(hào)的傳感器數(shù)目、振動(dòng)信號(hào)的分段數(shù)以及每個(gè)數(shù)據(jù)段包含的數(shù)據(jù)點(diǎn)數(shù)信息進(jìn)行建模，振動(dòng)信號(hào)中的時(shí)間序列信息被完全忽略，振動(dòng)信號(hào)包含的信息不完整，所以有必要將三維平行因子機(jī)械振源數(shù)估計(jì)方法擴(kuò)展至四維。目前，平行因子三維至四維的擴(kuò)展取得初步的進(jìn)展[15?17]。例如，文獻(xiàn)[15]提出一種基于四線性平行因子的雷達(dá)角度和頻率聯(lián)合估計(jì)算法。文獻(xiàn)[16]提出一種應(yīng)用于環(huán)境分析的交變加權(quán)剩余約束四次線性分解模型。這些文獻(xiàn)都表明四線性平行因子分解不僅保持了三線性分解唯一性的優(yōu)點(diǎn)，而且數(shù)據(jù)收斂更加平穩(wěn)，所含的信息更加全面，更不容易陷入局部最優(yōu)化。但是在機(jī)械振源數(shù)估計(jì)方面三維平行因子到四維平行因子的擴(kuò)展還是空白的。

為此，針對(duì)現(xiàn)有的三線性平行因子在故障盲分離中存在的不足，本文將三維平行因子擴(kuò)展至四維即引入（時(shí)間維）解決振動(dòng)信號(hào)時(shí)序信息被忽略的問題，提出了一種基于四線性平行因子的機(jī)械振源數(shù)估計(jì)方法。它是在三維的基礎(chǔ)上引入第四維（時(shí)間維）并將四線性平行因子盲分離方法和核一致檢測(cè)相結(jié)合，利用四線性交替最小二乘進(jìn)行更新擬合，并且得出了最佳組分?jǐn)?shù)下的載荷矩陣，能夠有效地估計(jì)振源數(shù)目。

1 四線性平行因子模型

四線性成分模型分解如圖1所示。

其中，Xq為一個(gè)四維矩陣，將Xq分解為大小分別為的相關(guān)矩陣A，B，C，D。G為一個(gè)維數(shù)為，并且超對(duì)角元素為1，其他元素為0的四維核對(duì)角矩陣，G也是一個(gè)四維殘差矩陣;Eq為四維殘差矩陣。

四維矩陣的四線性成分模型標(biāo)量形式通常可以表示為

四線性平行因子模型是基于四線性成分模型分解理論，采用四線性交替最小二乘理論得到模型的最優(yōu)解。四線性平行因子模型將四維矩陣X鋪展成二維矩陣形式，沿四個(gè)方向進(jìn)行交替分解得到，其有如下四種不同的模型表述形式

式中 是對(duì)角化算子，表示選矩陣A的第i行作為新生成矩陣的主對(duì)角線元素，矩陣其余的位置均為零。其他對(duì)角化算子，，表示含義與表示的含義相似。

2 基于振源估計(jì)的四線性平行因子盲分離模型構(gòu)建

對(duì)于N個(gè)源信號(hào)構(gòu)成的信號(hào)向量集，它的線性瞬時(shí)混疊模型可以表示為

式中 A為L(zhǎng)×N維的混合矩陣，為N個(gè)源信號(hào)殘余向量集。為L(zhǎng)維觀測(cè)信號(hào)。假定一個(gè)時(shí)間段內(nèi)每一個(gè)傳感器采集M個(gè)數(shù)據(jù)點(diǎn)（共N個(gè)傳感器），將傳感器采集到的信號(hào)中心化處理，然后將進(jìn)行中心化處理后的觀測(cè)信號(hào)均分成不重疊的J個(gè)數(shù)據(jù)段，每一個(gè)數(shù)據(jù)段包含M/J個(gè)數(shù)據(jù)點(diǎn)記其為K，每一個(gè)數(shù)據(jù)段對(duì)應(yīng)的采集時(shí)間為h，則共分為t/h個(gè)時(shí)間段記其為I。則線性混疊模式也可以表示為

3 振源數(shù)的估計(jì)

四維數(shù)據(jù)用四線性平行因子分析方法計(jì)算其最佳組分?jǐn)?shù)時(shí)，用核一致診斷算法（CORCONDIA）[18]來預(yù)先估計(jì)正確的成分?jǐn)?shù)來確定機(jī)械振動(dòng)信號(hào)的振源數(shù)。核一致診斷法通過計(jì)算核一致值（core?consistency）來確定體系的成分?jǐn)?shù)，其計(jì)算公式如下

式中 是模型的組分?jǐn)?shù);式（14）反映了不同組分?jǐn)?shù)時(shí)理想情況下的核心陣與最小二乘擬合陣的擬合程度。為擬合陣G的元素;是超對(duì)角陣T的元素。T為平行因子模型中的超對(duì)角陣，它是在理想情況下取正確組分?jǐn)?shù)時(shí)用Tucker3[19]方法得到的核心陣;G為用Tucker3方法得到的最小二乘擬合陣。一般認(rèn)為核一致值為80%到100%模型有效，40%到80%之間的值表示模型可能有效，但有輕微的特異性或相關(guān)性，而低于40%的值意味著模型無效。

4 仿真研究

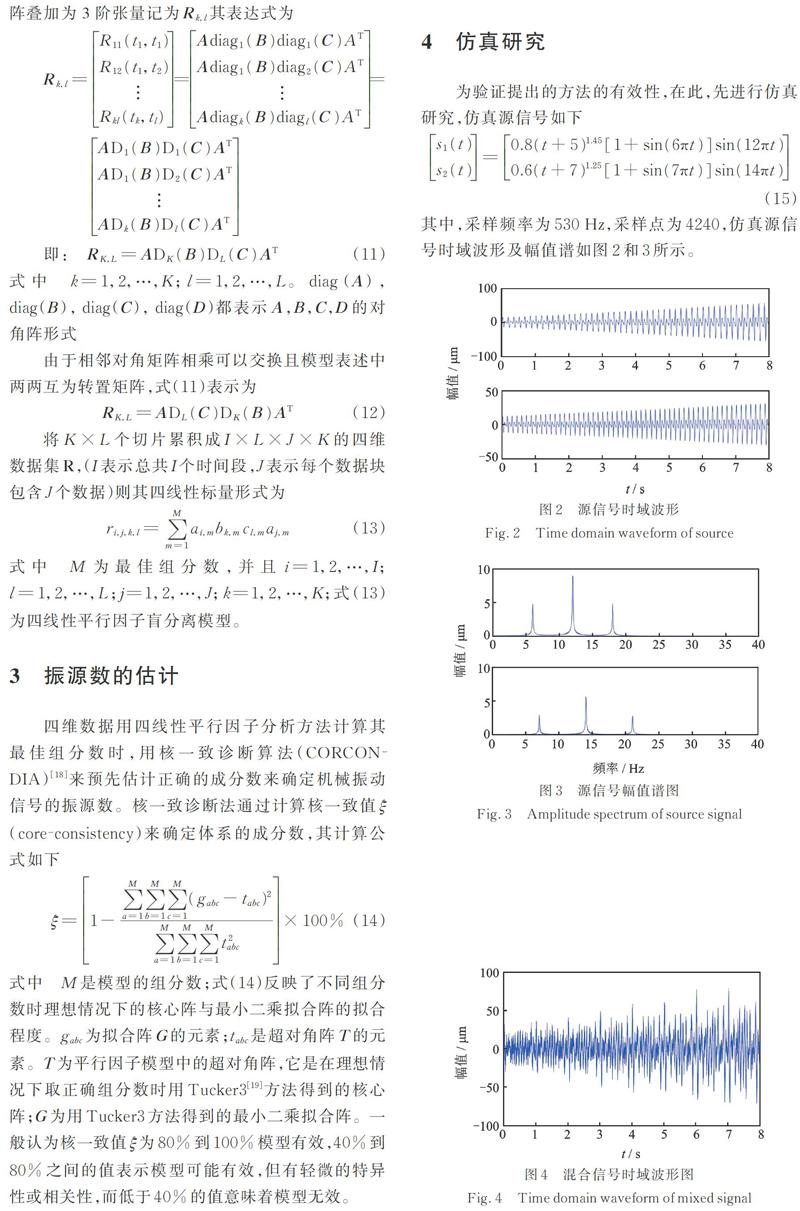
為驗(yàn)證提出的方法的有效性，在此，先進(jìn)行仿真研究，仿真源信號(hào)如下

其中，采樣頻率為530 Hz，采樣點(diǎn)為4240，仿真源信號(hào)時(shí)域波形及幅值譜如圖2和3所示。

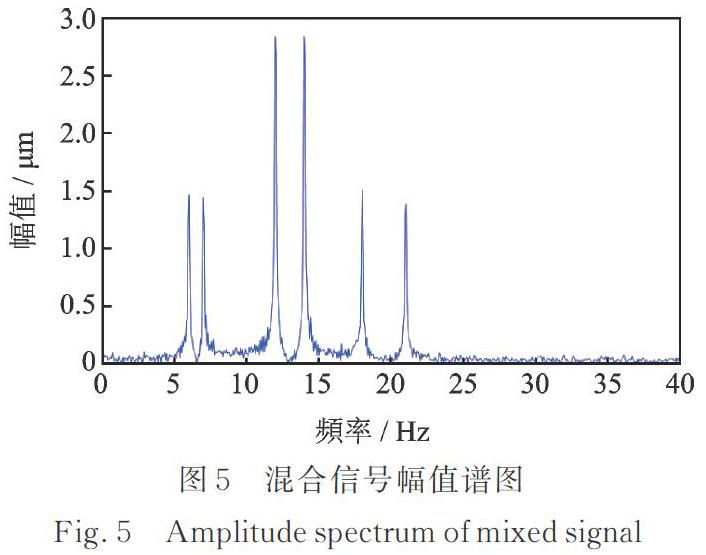
設(shè)置混合矩陣A為[0 1]區(qū)間的隨機(jī)數(shù)，根據(jù)線性瞬時(shí)混疊模型得到虛擬觀測(cè)信號(hào)。混疊后的虛擬觀測(cè)信號(hào)的時(shí)域波形圖和幅值譜圖分別如圖4和5所示。由圖4和5可知，在混合信號(hào)時(shí)域波形圖中無法辨識(shí)源信號(hào)特征頻率，兩個(gè)仿真信號(hào)的特征頻率完全混疊在一起。

通過核一致檢測(cè)算法估計(jì)最佳組分?jǐn)?shù)（即振源數(shù)），使用四線性最小二乘法進(jìn)行迭代，計(jì)算其核一致值、殘差平方和與迭代次數(shù)，若核一致值大于80%，且殘差平方和低于1000和迭代次數(shù)低于30000，算法有效（一般而言，殘差平方和為每一次迭代殘差平方的累加，當(dāng)殘差低于10-6并且不再減少時(shí)迭代結(jié)束）。

由圖6可知，當(dāng)組分?jǐn)?shù)為2時(shí)，核一致值為100%，當(dāng)組分?jǐn)?shù)為3時(shí)，核一致值為0。核一致值在2時(shí)滿足核一致檢測(cè)的條件并且在之后發(fā)生突變，當(dāng)組分?jǐn)?shù)為2時(shí)，迭代次數(shù)低于30000，殘差平方和小并且滿足限制條件，說明最佳組分?jǐn)?shù)值為2即振源數(shù)為2，算法有效。在組分?jǐn)?shù)值為2時(shí)得到的4個(gè)分解載荷如圖7所示，載荷矩陣B，D分解形式相同，符合式（12）中四線性平行因子盲分離模型。

為了體現(xiàn)本文方法的優(yōu)越性，在此給出了三線性平行因子源數(shù)估計(jì)方法的結(jié)果，如圖8所示。當(dāng)組分?jǐn)?shù)為2時(shí)，核一致值為65%，當(dāng)組分?jǐn)?shù)為3時(shí)，核一致值為0，即振源數(shù)為2。雖然核一致值為2時(shí)滿足核一致檢測(cè)的條件，但是其核一致值低于80%，表明模型可能有效，即不能夠非常準(zhǔn)確估計(jì)振源數(shù)目。而本文提出的方法在組分?jǐn)?shù)為2時(shí)，核一致值為100%，組分?jǐn)?shù)為3時(shí)，核一致值為0，表明模型有效，且能夠非常準(zhǔn)確地估計(jì)振源數(shù)目，而不是“可能”。這是因?yàn)樗木S平行因子振源數(shù)估計(jì)方法增加了振動(dòng)信號(hào)中的時(shí)間序列信息，包含信息更全面，得到的源數(shù)估計(jì)值也更加可靠。對(duì)比三線性平行因子同組分?jǐn)?shù)下的迭代次數(shù)，四線性迭代次數(shù)更少。對(duì)比同組分?jǐn)?shù)下殘差平方和，如表1所示，四線性平行因子的的殘差平方和更小，相比于三線性平行因子，收斂更加平穩(wěn)。

5 實(shí)驗(yàn)研究

為了進(jìn)一步驗(yàn)證四線性平行因子機(jī)械振源數(shù)估計(jì)方法的有效性，在此，將提出的方法應(yīng)用到機(jī)械設(shè)備滾動(dòng)軸承故障源數(shù)估計(jì)中。實(shí)驗(yàn)設(shè)備由一個(gè)小電機(jī)，傳感器，時(shí)間計(jì)數(shù)器，功率計(jì)等設(shè)備構(gòu)成。電機(jī)負(fù)載為0，電機(jī)轉(zhuǎn)速約1797 r/min，相應(yīng)的轉(zhuǎn)頻為fr=29.17 Hz，采樣頻率為48000 Hz，用電火花加工技術(shù)，分別在軸承內(nèi)圈和軸承外圈設(shè)置兩個(gè)故障。在驅(qū)動(dòng)端，軸承內(nèi)圈設(shè)置0.1778 mm的點(diǎn)蝕故障，軸承外圈設(shè)置0.5334 mm的點(diǎn)蝕故障。加速度傳感器安放在電機(jī)殼體上，用兩個(gè)加速度傳感器采集信號(hào)，采樣點(diǎn)數(shù)為10240，獲得2通道觀測(cè)信號(hào)，采集到的觀測(cè)信號(hào)時(shí)域波形如圖9所示。

首先，將采集到的數(shù)據(jù)進(jìn)行中心化處理，并將處理后的觀測(cè)信號(hào)分成不重疊的16段數(shù)據(jù)塊，相對(duì)應(yīng)的時(shí)間段為16，每一個(gè)數(shù)據(jù)段包含256個(gè)數(shù)據(jù)點(diǎn)。其次，將各段信號(hào)塊之間的時(shí)滯協(xié)方差疊加成3階并計(jì)算其時(shí)滯協(xié)方差矩陣，然后將這個(gè)3階張量在時(shí)間段上疊加為4階，用核一致診斷算法估計(jì)最佳組分?jǐn)?shù)（振源數(shù)），用四線性最小二乘法進(jìn)行迭代，計(jì)算其殘差平方和與迭代次數(shù)，得到的結(jié)果如圖10所示。

由圖10可知，當(dāng)組分?jǐn)?shù)為2時(shí)，迭代次數(shù)在合理的范圍，殘差平方和滿足限制條件并且核一致值遠(yuǎn)大于80%，當(dāng)組分?jǐn)?shù)等于3時(shí)核一致值接近0。核一致值在組分?jǐn)?shù)等于2時(shí)滿足核一致檢測(cè)的條件并且在組分?jǐn)?shù)等于3時(shí)發(fā)生突變，所以最佳組分?jǐn)?shù)為2，即振源為2。

6 結(jié)? 論

針對(duì)三線性平行因子只能對(duì)振動(dòng)信號(hào)的部分信息建模，信號(hào)中的時(shí)間序列信息被完全忽略的缺陷，本文提出一種基于四線性平行因子的機(jī)械振源數(shù)估計(jì)方法。該方法將三線性平行因子擴(kuò)展到四線性，增加了振動(dòng)信號(hào)時(shí)間序列信息，彌補(bǔ)了三線性建模時(shí)只能對(duì)部分信息建模的缺陷，使數(shù)據(jù)包含的信息更完整。用四線性交替最小二乘法擬合迭代，同組分?jǐn)?shù)下四線性得到的殘差平方和比三線性的更小，表明四線性平行因子相比于三線性收斂更加平穩(wěn)。用核一致診斷算法得到該模型下的最佳組分?jǐn)?shù)（振源數(shù)目），同組分?jǐn)?shù)條件下四線性比三線性得到的核一致值更高，更符合核一致估計(jì)條件。相比于三線性得到的可能有效的估計(jì)結(jié)果，四線性平行因子的估計(jì)更加準(zhǔn)確。最后利用仿真和實(shí)驗(yàn)驗(yàn)證了提出的方法的有效性。

參考文獻(xiàn)：

[1] Gelle G， Colas M， Servière C. Blind source separation： A new pre-processing tool for rotating machines monitoring？[J]. IEEE Transactions on Instrumentation and Measurement， 2003， 52（3）： 790-795.

[2] 成? 瑋，何正嘉，張周鎖. 基于獨(dú)立分量分析的殼體結(jié)構(gòu)振源數(shù)目估計(jì)方法[J]. 機(jī)械工程學(xué)報(bào)， 2014，50（19）： 73-79.

Cheng Wei， He Zhengjia， Zhang Zhousuo. Estimation method of vibration source number of shell structure based on independent component analysis[J]. Journal of Mechanical Engineering， 2014， 50（19）： 73-79.

[3] 李志農(nóng)， 呂亞平， 岳秀廷. 基于分?jǐn)?shù)Fourier變換的機(jī)械故障源盲分離方法的研究[J]. 軸承， 2010，（6）： 47-50.

Li Zhinong，Lü Yaping， Yue Xiuting. Research on blind separation of mechanical fault sources based on fractional Fourier transform [J]. Bearing，2010，（6）： 47-50.

[4] 毋文峰， 陳小虎， 蘇勛家， 等. 機(jī)械振動(dòng)源數(shù)估計(jì)的小波方法[J]. 機(jī)械科學(xué)與技術(shù)， 2011， 30（10）： 1679-1682.

Wu Wenfeng， Chen Xiaohu， Su Xunjia， et al. Wavelet method for estimating mechanical vibration sources[J]. Mechanical Science and Technology， 2011， 30（10）： 1679-1682.

[5] 張洪淵，賈? 鵬，史習(xí)智，等. 確定盲分離中未知信號(hào)源個(gè)數(shù)的奇異值分解法[J]. 上海交通大學(xué)學(xué)報(bào)，2001， 35（8）： 1155-1158.

Zhang Hongyuan， Jia Peng， Shi Xizhi， et al. Singular value decomposition method for determining the number of unknown signal sources in blind separation[J]. Journal of Shanghai Jiao Tong University， 2001， 35（8）： 1155-1158.

[6] LEl Huang， TEND Long， WU Shunjun. Source enumeration for high-resolution array processing using improved Gerschgorin radii without eigcn dccomposition[J]. IEEE Transactions on Signal Processing， 2008，56（12）： 5916-5925.

[7] Harshman R A. Determination and Proof of Minimum Uniqueness Conditions for PARAFAC[J]. UCLA Working Papers in Phonetics， 1972， 22（1）： 111-117.

[8] Carroll J D， Chang J J. Analysis of individual differences in multimensional scaling via an N-way generalization of “Eckart-Young” decomposition[J]. Psychometrika， 1970， 35（3）： 283-319.

[9] Lee B M， Seo Y S， Hur J. Investigation of adsorptive fractionation of humic acid on graphene oxide using fluorescence EEM-PARAFAC[J].Water Research，2015， 73： 242-251.

[10] Zhang Xiaofei， Cao Renzheng， Zhou Ming. Noncircular-PARAFAC for 2D-DOA estimation of noncircular signals in arbitrarily spaced acoustic vector-sensor array subjected to unknown locations[J]. EURASIP Journal on Advances in Signal Processing， 2013： 107

[11] 張卉楓. 三維化學(xué)計(jì)量學(xué)方法應(yīng)用于環(huán)境檢測(cè)和藥物分析[D]. 長(zhǎng)沙：湖南大學(xué)， 2007.

Zhang Huifeng. Application of three-dimensional chemometrics in environmental detection and drug analysis [D]. Changsha： Hunan University， 2007.

[12] 楊? 誠(chéng). 平行因子分析在多故障源盲分離中的應(yīng)用研究[D]. 南昌：南昌航空大學(xué)， 2018.

Yang Cheng. Application of parallel factor analysis in blind separation of multiple fault sources[D]. Nanchang： Nanchang Hangkong University， 2018.

[13] 許凌云. 陣列多參數(shù)聯(lián)合估計(jì)算法及應(yīng)用的研究[D]. 南京：南京航空航天大學(xué)，2012.

Xu Lingyun. Research on the algorithm and application of array multi-parameter joint estimation [D]. Nanjing：Nanjing University of Aeronautics and Astronautics， 2012.

[14] 楊? 誠(chéng)， 李志農(nóng). 采用PARAFAC的欠定盲分離中機(jī)械振源數(shù)估計(jì)方法[J].華僑大學(xué)學(xué)報(bào)（自然科學(xué)版）， 2018， 39（3）： 337-342.

Yang Cheng， Li Zhinong. Using PARAFAC's method for estimating the number of mechanical vibration sources in underdetermined blind separation[J]. Journal of Overseas Chinese University （Natural Science Edition）， 2018， 39（3）： 337-342.

[15] 李建峰， 張小飛. 基于四線性分解的雙基地MIMO雷達(dá)的角度和多普勒頻率聯(lián)合估計(jì)[J]. 航空學(xué)報(bào)， 2012， 33（8）： 1474-1482.

Li Jianfeng， Zhang Xiaofei. Joint angle and Doppler frequency estimation of bistatic MIMO radar based on quadrilinear decomposition[J]. Acta Aeronautica et Astronautica Sinica， 2012， 33（8）： 1474-1482.

[16] Liu Tingting， Zhang Ling， Wang Shutao， et al. Four-dimensional data coupled to alternating weighted residue constraint quadrilinear decomposition model applied to environmental analysis： Determination of polycyclic aromatic hydrocarbons[J]. Spectrochimica Acta Part A， Molecular and Biomolecular Spectroscopy， 2018，193： 507-517.

[17] Wang Z， Cai C， Wen F， et al. A quadrilinear decomposition method for direction estimation in bistatic MIMO radar[J]. IEEE Access， 2018， 6： 13766-13772.

[18] Bro R， Kiers H A. A new efficient method for determining the number of components in PARAFAC models[J]. Journal of Chemometrics， 2003， 17（5）： 274-286.

[19] Tucker L. Some mathematical notes on three-mode factor analysis[J]. Psychometrika， 1966， 31： 279-311.

作者簡(jiǎn)介： 李志農(nóng)（1966-），男，教授。E-mail：lizhinong@tsinghua.org.cn