不銹鋼激光深熔焊熔池動(dòng)態(tài)行為數(shù)值模擬

何林基 張?zhí)炖? 徐剛 馬春偉

摘 要： 考慮激光深熔焊過程中存在對(duì)流、輻射、熱傳導(dǎo)等傳熱過程以及蒸汽反沖作用力，表面張力，熱浮力等力學(xué)過程，采用移動(dòng)旋轉(zhuǎn)高斯體熱源來簡(jiǎn)化焊接的熱過程，使用VOF方法跟蹤自由界面，通過焓孔隙法實(shí)現(xiàn)焊接過程的凝固熔化，同時(shí)采用連續(xù)表面張力模型將蒸汽反沖作用力轉(zhuǎn)化為在一定厚度上連續(xù)的作用力。建立數(shù)學(xué)模型，獲得了奧氏體不銹鋼深熔焊接過程中動(dòng)態(tài)熔池的溫度場(chǎng)以及流場(chǎng)分布。結(jié)果表明小孔存在周期性的震蕩，小孔壁面在蒸汽反沖作用力、表面張力、流體靜壓力下形成凸臺(tái)。凸臺(tái)再隨著小孔周期性的震蕩則會(huì)形成氣孔，產(chǎn)生缺陷。焊接試驗(yàn)的焊縫橫截面熔合線同模型計(jì)算結(jié)果相吻合，驗(yàn)證了模型的可靠性。

關(guān)鍵詞： 激光深熔焊;熔池流場(chǎng);小孔行為;熔池震蕩

文章編號(hào)： 2095-2163（2021）03-0124-07 中圖分類號(hào)：TG402 文獻(xiàn)標(biāo)志碼：A

【Abstract】Considering the heat transfer process such as convection， radiation， heat conduction and steam recoil force， surface tension， thermal buoyancy and other mechanical processes in the laser deep penetration welding process， a moving and rotating Gaussian heat source is used to simplify the thermal process of welding， and the VOF method is used to is track the free interface， the solidification and melting of the welding process is realized by the enthalpy pore method， and the continuous surface tension model is used to convert the steam recoil force into a continuous force on a certain thickness. A mathematical model is established to obtain the temperature field and flow field distribution of the dynamic molten pool during the deep penetration welding of austenitic stainless steel. The results show that the small holes have periodic oscillations， and the walls of the holes form bosses under the steam recoil force， surface tension， and hydrostatic pressure. When the boss oscillates with the keyholes， pores will be formed， resulting in defects. The weld cross-section fusion line of the welding test is consistent with the calculation result of the model， which proves the accuracy of the model.

【Key words】 laser deep penetration welding; molten pool flow field; keyhole behavior; molten pool oscillation

0 引 言

作為易于實(shí)現(xiàn)自動(dòng)化控制且具有廣闊發(fā)展前景的先進(jìn)焊接技術(shù)，激光焊接是一種重要的現(xiàn)代材料加工技術(shù)[1]，具有大的焊縫深寬比，焊接速度快，工件變形小，熱影響的區(qū)域小，同時(shí)也有著較高的組裝精度，較低的焊接雜質(zhì)含量，良好的焊接接頭機(jī)械性能等特點(diǎn)[2] 。從上世紀(jì)70年代開始，國內(nèi)外學(xué)者即已使用數(shù)值模擬方法對(duì)激光深熔焊的熔池和熔池小孔的動(dòng)態(tài)行為進(jìn)行了深入的研究[3]。Ki等人[4-5]考慮到激光焊接過程中材料對(duì)于激光的菲涅爾吸收，以及材料蒸發(fā)引起的均勻沸騰，建立了三維激光焊接小孔模型。 Volpp等人 [6]基于壓力和能量平衡，根據(jù)不同的入射光束強(qiáng)度分布，計(jì)算不同深度的初始小孔半徑。通過使用光線跟蹤方法、包括多次反射來改善小孔形狀的計(jì)算，提出了激光深熔焊匙孔的解析模型。龐盛永[7]采用level set法對(duì)熔池的自由界面進(jìn)行實(shí)時(shí)的計(jì)算，并考慮到表面張力、反沖壓力、熱毛細(xì)作用和保護(hù)氣體對(duì)熔池的作用，建立關(guān)于熔池內(nèi)部流動(dòng)和小孔的形成過程的數(shù)值模型。

綜上論述可知，本文即在探討深熔焊過程中熔池表面的熱傳導(dǎo)、表面張力、蒸汽反沖壓力，熱浮力對(duì)熔池的作用、以及自由界面的散熱結(jié)合流體動(dòng)力學(xué)原理的基礎(chǔ)上，建立激光深熔焊熔池及小孔的三維瞬態(tài)數(shù)學(xué)模型，對(duì)小孔的演變過程以及小孔的震蕩行為進(jìn)行了研究。

1 模型建立

1.1 模型的控制方程

激光深熔焊物理過程異常復(fù)雜，其中涉及到材料的熔化與凝固，同時(shí)也要考慮金屬蒸汽的反沖壓力對(duì)熔池的擠壓從而形成匙孔。為了簡(jiǎn)化模型，這里給出如下基本假設(shè)[8]：

（1）熔池中的液態(tài)金屬假設(shè)為層流且不可壓縮。

（2）該材料是各向同性的，熱物理性質(zhì)除沸點(diǎn)外，僅取決于溫度。固-液相變時(shí)金屬液體密度不發(fā)生顯著變化。

（3）不考慮金屬蒸汽、等離子體以及保護(hù)氣體對(duì)熔池的影響。

（4）不考慮熔體與氣體間的化學(xué)反應(yīng)。

基于此，進(jìn)一步給出計(jì)算模型的質(zhì)量、動(dòng)量、能量守恒的方程具體如下。

其中， A、B0表示與材料相關(guān)的常數(shù);U表示每個(gè)原子的蒸發(fā)潛熱;T表示小孔的壁面溫度;k表示玻爾茲曼常數(shù)。

在自由界面上，由于菲涅爾吸收，輻射以及熱對(duì)流的作用，自由界面的溫度邊界條件可以寫為：

由于激光焊接過程中的熱流密度在厚度方向上遞減，因此采用旋轉(zhuǎn)高斯曲面熱源模型，即：

其中，η為熱效率，本文中取0.7;H為熱源高度;R為熱源最大有效半徑。

1.2 自由界面的追蹤與熔化凝固的處理

在計(jì)算過程中，氣液界面是動(dòng)態(tài)變化的，使用VOF法對(duì)自由界面進(jìn)行追蹤，通過求解金屬體積分?jǐn)?shù)Φ的連續(xù)性方程，可以獲得金屬體積分?jǐn)?shù)隨時(shí)間演變的空間分布函數(shù)。Φ的值域區(qū)間為[0～1]，當(dāng)網(wǎng)格單元體積分?jǐn)?shù)值Φ=1時(shí)，單元全部為液態(tài)金屬相。當(dāng)網(wǎng)格單元體積分?jǐn)?shù)值Φ=0時(shí)，單元全部為氣相。當(dāng)網(wǎng)格單元體積分?jǐn)?shù)值位于0～1時(shí)，單元既有液態(tài)金屬相、也有氣相，這些單元所形成的面即為自由界面 [10]。其方程滿足：

焊接過程中的相變釋放的熱能通過液相體積分?jǐn)?shù)法處理，糊狀區(qū)域的動(dòng)量損失采用焓-孔隙度法[11]近似。用多孔介質(zhì)處理相變的控制體，孔隙度等于液相體積分?jǐn)?shù)f1;通過計(jì)算每個(gè)控制體來計(jì)算固液界面。糊狀區(qū)為液相分?jǐn)?shù)在0～1之間的區(qū)域，看作孔隙度從0到1遞增的多孔介質(zhì)，動(dòng)量損失源Smush滿足：

其中，ε為取值很小的常數(shù);Amush為與糊狀區(qū)枝晶尺寸有關(guān)的常數(shù);ν為該單元的速度矢量。

1.3 自由界面力與熱能的處理

本文使用連續(xù)表面力模型對(duì)蒸汽反沖作用力，表面張力等界面力進(jìn)行轉(zhuǎn)化，其核心思想是將界面上的面作用（壓力或剪切力）轉(zhuǎn)化為在一定厚度區(qū)域內(nèi)的連續(xù)作用[12]。法向力的CSF計(jì)算公式如下：

1.4 邊界條件

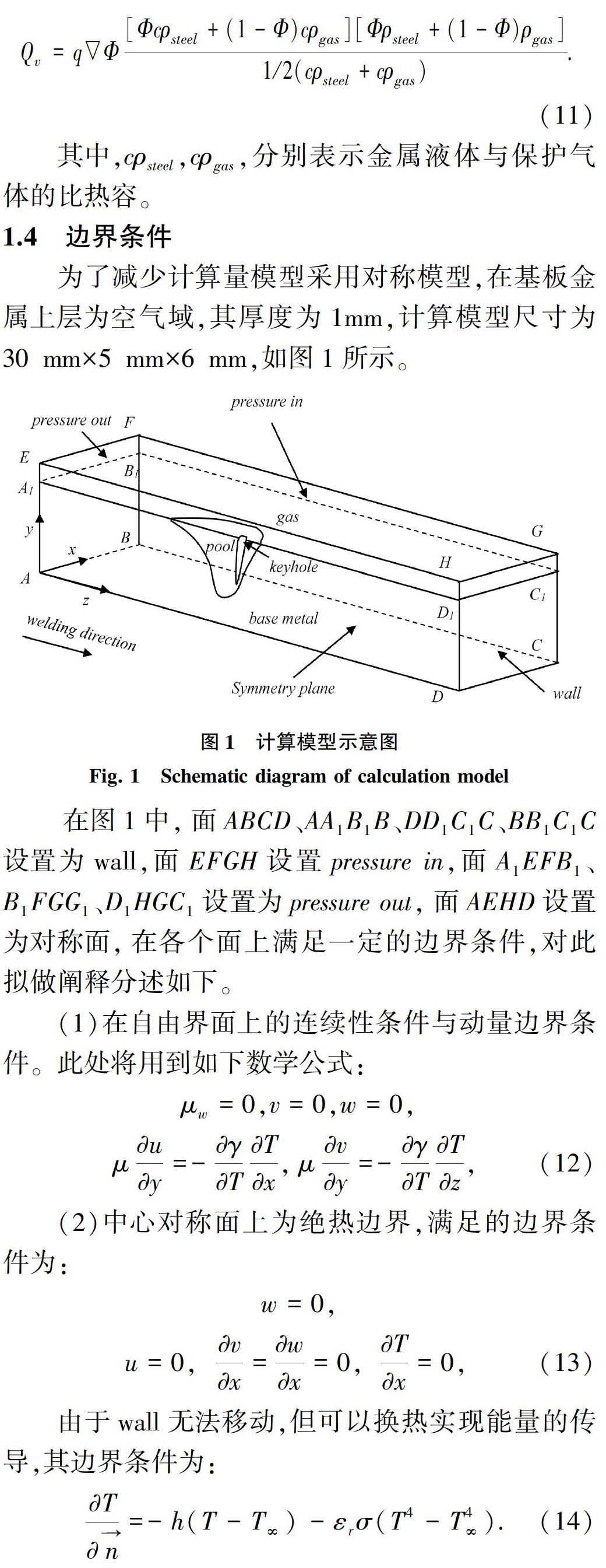
為了減少計(jì)算量模型采用對(duì)稱模型，在基板金屬上層為空氣域，其厚度為1mm，計(jì)算模型尺寸為30mm×5mm×6mm，如圖1所示。

在圖1中，面ABCD、AA1B1B、DD1C1C、BB1C1C設(shè)置為wall，面EFGH設(shè)置pressure in，面A1EFB1、B1FGG1、D1HGC1設(shè)置為pressure out，面AEHD設(shè)置為對(duì)稱面，在各個(gè)面上滿足一定的邊界條件，對(duì)此擬做闡釋分述如下。

（1）在自由界面上的連續(xù)性條件與動(dòng)量邊界條件。此處將用到如下數(shù)學(xué)公式：

由于wall無法移動(dòng)，但可以換熱實(shí)現(xiàn)能量的傳導(dǎo)，其邊界條件為：

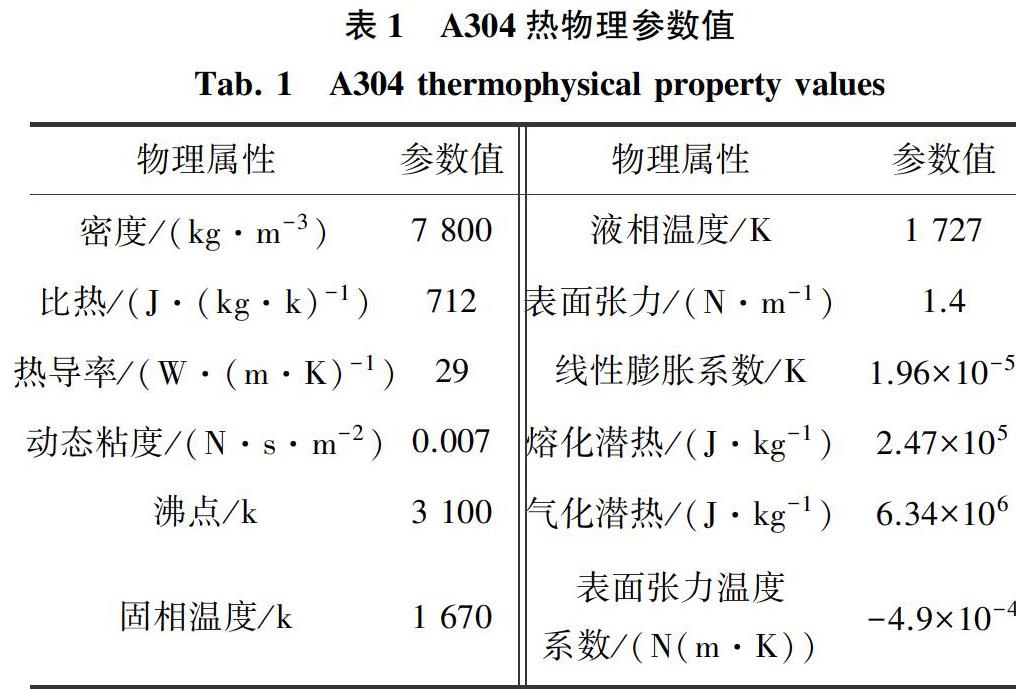
1.5 材料熱物理參數(shù)

材料為奧氏體不銹鋼，主要材料熱物理屬性見表1。焊接采用光纖激光器，輸出功率為3 KW，焊接速度為1.5 m/min，光斑直徑為0.8 mm。

2 計(jì)算結(jié)果及討論

2.1 焊縫縱截面溫度場(chǎng)及流場(chǎng)

圖2為焊縫縱截面小孔及溫度場(chǎng)演變過程。圖2（a）、圖2（b）、圖2（c）、圖2（d ）分別為t0、t1、t2、t3時(shí)焊縫縱截面的溫度場(chǎng)。在t0時(shí)刻，焊縫區(qū)域并沒有小孔的形成。隨著持續(xù)的熱輸入的增加，焊縫表面在反沖力的作用下出現(xiàn)明顯的下凹， 在t1時(shí)出現(xiàn)穩(wěn)定的匙孔，在t3時(shí)刻小孔的尺寸進(jìn)一步地?cái)U(kuò)大，深度達(dá)到1.5 mm，寬度達(dá)到1.2 mm。由公式（5）可知，熔池蒸汽所產(chǎn)生的反沖作用力是隨著溫度的增加而升高，隨著熱源的作用時(shí)間增加，使得熔池中心溫度急劇升高，反沖作用力也隨之增加，從而使得小孔深也在增加。

圖3為在t2、t3時(shí)刻熔池的速度場(chǎng)分布。從圖3（a）中，可以看到在小孔的底部的金屬液體受到反沖作用力向下流動(dòng)，并沿著小孔尾部向熔池后部流動(dòng)。這使得金屬液體向下流動(dòng)，將熱量帶向熔池底部，增加了熔池的深度。同時(shí)，將熱量傳遞到熔池后部，增大了熔池的面積。圖3（b）、圖3（d）中可以看出熔池中心區(qū)域的金屬液體在表面張力的作用下向熔池邊緣流動(dòng)。圖3（c）中小孔的尾部與前端都存在渦流，沿著小孔壁面向上流動(dòng)，到熔池上部后在靜水壓的作用下，向熔池下部流動(dòng)。同時(shí)在小孔的后壁存在一個(gè)凸臺(tái)，由于熱源的移動(dòng)使得熔池后部溫度下降，表面張力作用增加，反沖力作用減小，同時(shí)受到流體的沖擊力等使得金屬液體形成凸臺(tái)。隨著熱源的移動(dòng)，小孔尾部形成的凸臺(tái)向小孔前端壁面傾斜。凸臺(tái)同小孔前端接觸，使得小孔閉合，成一個(gè)封閉的空腔，空腔若是在熔池流動(dòng)的過程中未能運(yùn)動(dòng)到熔池表面，就會(huì)形成氣孔，這是激光焊接過程中常見的缺陷[13]。

2.2 沿焊縫橫向熔池溫度場(chǎng)及流場(chǎng)

為了研究同一時(shí)刻時(shí)焊接熔池的溫度場(chǎng)以及流場(chǎng)，選取計(jì)算時(shí)間為0.54 s時(shí)焊接熔池的橫截面進(jìn)行觀察。選取計(jì)算結(jié)果的位置如圖4所示。

0.54 s熔池橫截面溫度以及流場(chǎng)演變?nèi)鐖D5所示。由圖5（a）可知，熔池尾部離激光光源中心較遠(yuǎn)，熔池的溫度開始下降，非中心區(qū)域的金屬液體開始凝固，使得熔池的面積減小。同時(shí)由于焊縫上表面對(duì)于熔池金屬液體的表面張力作用，使得部分金屬液體向焊縫邊緣流動(dòng)，形成回流。圖5（b）中，小孔后壁處溫度較小孔中心區(qū)域較低，但是反沖作用力仍可以對(duì)熔池作用，使其產(chǎn)生下凹，同時(shí)在表面張力作用下，熔池中心區(qū)金屬液體向上流動(dòng)，遇到固相壁面形成回流，使得熔池充分地流動(dòng)。圖5（c）位于熱源中心，熔池溫度最高，使得中心區(qū)域的金屬熔化并且等離子體化，金屬等離子蒸汽產(chǎn)生的反沖作用力使得金屬液體向下流動(dòng)，形成小孔，同時(shí)將熱量沿厚度方向傳遞，達(dá)到熔池的最大熔深。圖 5（d）位于小孔的前壁，熔池中心區(qū)域溫度接近小孔中心溫度，金屬液體在反沖作用力下，向下凹陷變形。

2.3 熔池和小孔的震蕩行為

小孔行為對(duì)熔池溫度場(chǎng)和流場(chǎng)影響很大。小孔深度不同，熔池的形狀、溫度場(chǎng)分布和流動(dòng)模式也顯著不同 [14]。

圖6展示了模擬所得小孔深度以及寬度隨時(shí)間變化情況。由圖6分析可知，小孔幾何尺寸的變化是伴隨激光光源移動(dòng)，小孔不斷生成，坍縮的過程。從圖6中可以看出小孔深度變化與寬度變化是同步的。小孔的形成與坍縮的一個(gè)周期大約在10～40 ms之間。小孔最大深度可達(dá)到1.6 mm，在1.2 mm到0.8 mm之間浮動(dòng)。激光焊接過程中的小孔可以分為2個(gè)階段：小孔的快速形成與動(dòng)態(tài)平衡[15]。在開始階段，材料在激光光源的作用下，開始熔化、蒸發(fā)產(chǎn)生等離子體，由此形成的向下的蒸汽反沖力直接作用于熔化的金屬上，流動(dòng)的金屬不存在剛度，熔池迅速變形，向下凹陷，形成小孔。同時(shí)，流動(dòng)的金屬液體將熱能帶到了熔池的底部，使得小孔在深度方向進(jìn)一步拓展。當(dāng)小孔達(dá)到一定深度后，材料的熔化與蒸發(fā)消耗了大量的熱量，隨著激光光源的移動(dòng)，使得在厚度方向上能量密度下降，反沖作用力也隨之降低，同時(shí)在表面張力、流體的靜水壓力的作用下，使得小孔無法維持并閉合。在反沖力、表面張力、流體靜壓力的平衡過程中，小孔處于動(dòng)態(tài)平衡。直到沿厚度方向上的能量密度上升，小孔深度開始增加，并重復(fù)上過程。

2.4 實(shí)驗(yàn)驗(yàn)證

為了驗(yàn)證模型預(yù)測(cè)的可靠性以及提升預(yù)測(cè)精度，對(duì)模擬過程進(jìn)行了工藝試驗(yàn)，利用焊縫橫截面熔合線的位置、熔池深度以及熔池寬度校準(zhǔn)并驗(yàn)證模型的準(zhǔn)確性。圖 7 展示了焊縫橫斷面形狀計(jì)算結(jié)果和實(shí)驗(yàn)結(jié)果的對(duì)比情況。

從圖7中可見，計(jì)算熔合線形狀和實(shí)驗(yàn)結(jié)果吻合較好，表明建立的激光深熔焊接模型可以較為準(zhǔn)確地預(yù)測(cè)該激光焊接過程傳熱和熔池流動(dòng)的特點(diǎn)，對(duì)于焊接過程有更直觀的研究。

3 結(jié)束語

（1）本文考慮焊接過程中反沖壓力、表面張力、流體靜水壓力等作用，通過有限元建立了激光深熔焊熔池的計(jì)算模型，試驗(yàn)驗(yàn)證同計(jì)算結(jié)果吻合。

（2）激光深熔焊過程中熔池形成的小孔并非幾何規(guī)則，是反沖作用力、表面張力、流體靜壓等力不斷平衡的結(jié)果。小孔壁面所形成的凸臺(tái)的行為可能會(huì)導(dǎo)致氣孔的產(chǎn)生。

（3）激光深熔焊接的過程中，是伴隨小孔的形成與動(dòng)態(tài)平衡的過程，熔池的尺寸的變化同小孔的尺寸變化是相關(guān)的。

參考文獻(xiàn)

[1] 鄧集權(quán). 激光深熔焊接小孔和熔池動(dòng)態(tài)行為的模擬與試驗(yàn)研究[D]. 長(zhǎng)沙：湖南大學(xué)，2016.

[2] 霍厚志. 激光深熔焊過程仿真技術(shù)研究[D]. 太原：太原科技大學(xué)，2012.

[3] 夏勝全，何建軍，王巍，等. 激光深熔焊熔池三維瞬態(tài)行為數(shù)值模擬[J]. 中國激光，2016，43（11）：1102004（1）-（12）.

[4] KI H， MAZUMDER J， MOHANTY P S. Modeling of laser keyhole welding： Part I. mathematical modeling， numerical methodology， role of recoil pressure， multiple reflections， and free surfaceevolution[J]. Metallurgical and Materials Transactions A，2002，33：1817-1830.

[5] KI H， MAZUMDER J， MOHANTY P S. Modeling of laser keyhole welding： Part II.simulation of keyhole evolution， velocity， temperature profile， and experimental verification[J]. Metallurgical and Materials Transactions A，2002，33：1831-1842 .

[6] VOLPP J， VOLLERTSEN F. Analytical modeling of the keyhole including multiple reflections for analysis of the influence of different laser intensity distributions on keyhole geometry[J]. Physics Procedia，2013，41：460-468.

[7] 龐盛永. 激光深熔焊接瞬態(tài)小孔和運(yùn)動(dòng)熔池行為及相關(guān)機(jī)理研究[D]. 武漢：華中科技大學(xué)，2011.

[8] 吳向陽，徐劍俠，高學(xué)松，等. 激光-MIG復(fù)合焊接熱過程與熔池流場(chǎng)的數(shù)值分析[J]. 中國激光，2019，46（9）：0902003（1）-（12）.

[9] MATSUNWA A， SEMAK V. The simulation of front keyhole wall dynamics during Laser welding[J]. Journal of physics D，1997，30（5）：798-809.

[10]MENG Xiangmeng， ARTINOV M， BACHMANN M， et al. Experimental and numerical assessment of weld pool behavior and final microstructure in wire feed laser beam welding with electromagnetic stirring[J]. Journal of Manufacturing Processes，2019，45：408-418.

[11]AI Yuewei， JIANG Ping， WANG Chunming，et al. Experimental and numerical analysis of molten pool and keyhole profile during high-power deep-penetration laser welding[J]. International Journal of Heat and Mass Transfer，2018，126（Pt A）：779-789.

[12]孟祥萌. 高速GTAW焊縫表面成形缺陷的形成機(jī)理及其抑制措施[D]. 濟(jì)南：山東大學(xué)，2017.

[13]鞏水利，龐盛永，王宏，等. 激光焊接熔池動(dòng)力學(xué)行為[M]. 北京：航空工業(yè)出版社，2018.

[14]CHEN Minghua， XU Jiannan， XIN Lijun， et al. Effect of keyhole characteristics on porosity formation during pulsed laser-GTA hybrid welding of AZ31B magnesium alloy[J]. Optics and Lasers in Engineering，2017，93：139-145.

[15]吳向陽，徐劍俠，高學(xué)松，等. 激光-MIG復(fù)合焊接熱過程與熔池流場(chǎng)的數(shù)值分析[J]. 中國激光，2019，46（9）：0902003（1）-（12）.