基于DTW-LSTM的短期樓宇電力負荷預測方法*

張明理， 張明慧， 王 勇， 武志鍇， 滿林坤

(1. 東北大學 軟件學院， 沈陽 110169； 2. 國網遼寧省電力有限公司 a. 經濟技術研究院， b. 財務資產部， 沈陽 110015)

在增量配電網投資管理中，因為樓宇用電行為對大型園區能耗影響較大，故針對樓宇電力負荷預測具有較為重要意義[1].鑒于電能難以存儲的特性，電企的生產能力應該能夠根據實際用電進行動態調整.樓宇用電作為電能主要用途之一，對樓宇短期的電力負荷精準預測既可以降低電能的損耗，又能保證用電環境的安全與穩定.

智能電網是未來電網發展的必然趨勢[2]，智能電網的重要組成部分是安裝在各個樓宇中的智能電表，其可定期發送和接收樓宇與供電商之間的用電量信息，且隨著數據存儲和處理器功能的增強，可以將獲得的大量樓宇用電數據以時間序列的形式進行存儲，對數據進行處理后，即可預測未來的用電情況.

在過去的幾十年中，學者們提出的眾多統計和人工智能方法應用于短期電力負荷預測.李澤文等[3]利用時間序列分析和加權最小二乘法建立ARMA模型，實現短期的負荷預測，但最終預測精度仍有較大的提升空間.許言路等[4]發現，隨著神經網絡的興起，卷積神經網絡(CNN)在多個方面均表現出卓越的貢獻，在具有時間序列特征的電力負荷預測方面也有優越表現.余登武等[5]提出利用深度卷積神經網絡(DCNN)模型來預測加拿大維多利亞市一周中每一天的用電負荷，但隨著網絡深度的增加，預測精度會趨于飽和甚至下降.此外，循環神經網絡(RNN)使用也較為普遍，其中最為著名的是長短期記憶(LSTM)循環神經網絡.李鵬輝等[6]提出一種基于LSTM的短期高壓負荷回歸預測方法，通過引入自循環權重，各單元彼此循環連接，動態化地改變積累時間尺度，使其具有長短期記憶并表現出優異的性能.

僅使用統計方法或人工智能方法進行短期負荷預測精度受限，故結合聚類算法對用電行為進行分析的想法被提出.艾欣等[7]應用K-Means、K-Medoid和SOM聚類算法，根據家庭一天的用電模式劃分為簇，并產生能代表家庭內常見用電模式的曲線；趙凱等[8]將SOM與K-Means算法相結合應用于工業建筑能耗模式分析，并成功識別出不同的能耗及相關行為模式；史靜等[9]根據用戶消費模式的相似性，利用周期性分析和K-Means聚類算法將用戶進行分組.然而現在大多數傳統聚類算法會導致簇數過多，其中每個用電曲線可能與多個簇有關，用電曲線無法確定固定的模式.針對上述問題，本文的貢獻如下：

1) 采用一種基于形狀的動態時間規整(DTW)聚類算法對樓宇日用電曲線進行聚類，并對聚類結果進行編碼.

2) 利用馬爾科夫鏈模型，根據樓宇過去10天用電曲線所屬簇的編碼對未來一天的用電曲線編碼進行預測，該步驟的目的是預測出未來一天的用電曲線原型.

3) 以編碼為特征，通過LSTM網絡，根據樓宇歷史用電數據對樓宇未來的短期負荷進行預測.

4) 將DTW-LSTM短期負荷預測模型與LSTM模型進行對比實驗，由此分析DTW聚類對預測精度的提升效果.其次針對傳統的短期負荷預測SVR模型做出對比實驗，從而說明本文所提出模型最終的效果.

1 DTW-LSTM模型

1.1 DTW聚類算法

對于樓宇的用電曲線，傳統聚類算法采用的是基于歐式距離的度量，其只能對同一時刻的用電數據進行相似評估.樓宇的用電曲線可能在兩個不同時間段具有相似的用電行為，若繼續采用基于歐式距離度量的聚類算法，則可能最終的聚類效果較差且具有較多的簇數目[10].

DTW算法專門用于處理衡量時間序列相似度問題，通過在時間軸上的非線性拉伸或收縮進行兩條用電曲線的形狀匹配.算法具體描述如下：比較兩個長度為N的時間序列X和Y，首先需要定義一條規整路徑p=(p1，p2，…，pL)，其中pi=(ni，mi)∈[1∶N]×[1∶N](1≤i≤L).規整路徑需要滿足以下條件：

1) 邊界條件.其中p1=(1，1)，并且pL=(N，N).

2) 單調性.路徑上的每個點必須隨著時間單調進行變化，故ni和mi滿足n1≤ni≤nL，m1≤mi≤mL.

3) 連續性.對于路徑上一點pi=(ni，mi)及下一個點pi+1=(ni+1，mi+1)滿足ni+1-ni≤1，且mi+1-mi≤1.

滿足上述條件后，根據d(xn，ym)=(xn-ym)2，可以計算時間序列X與Y之間的規整路徑總代價為

(1)

最優規整路徑p*是所有可能的規整路徑中，總代價最小的一條.序列X與Y之間的DTW距離即為最優規整路徑總代價，定義為

dDTW(X，Y)=cp*(X，Y)

(2)

p*=arg mincp(X，Y)

(3)

為了計算兩條負荷曲線的DTW距離，找到最優的規整路徑，本文利用動態規劃思想求解.首先計算時間序列X與Y中每兩個點之間的距離，并利用一個代價矩陣C保存.最優規整路徑的總代價可以遞歸計算，遞歸公式為

dDTW(xi，yj)=d(xi，yj)+min(dDTW(xi-1，yj)，

dDTW(xi，yj-1)，dDTW(xi-1，yj-1))

(4)

最終dDTW(xN，yN)即為最佳規整路徑的總代價.給定樓宇負荷曲線序列X，聚類數目K，每個簇的原型設為uk.基于DTW的聚類算法目的是找到K個簇的DTW距離之和最小，即

(5)

因此，通過DTW算法進行聚類得到的每個簇的用電曲線中相同時刻的用電情況可能差異較大，但整體用電規律是相似的.

1.2 馬爾科夫鏈模型

馬爾科夫鏈過程是以系統狀態轉移規律作為基礎，研究和分析事物的發展趨勢，從而推導出事物未來最有可能出現的狀態[11].

選取歷史編碼作為劃分系統狀態的根據，設編碼序列共包含r種狀態，記為s1，s2，…，sr.當聚類數目為K類時，其中的某個狀態si的取值范圍為[0，K-1].歷史的編碼數據從si狀態經過n步轉移到sj狀態的概率為

Pij(n)=Mij(n)/Mi

(6)

式中：Mij(n)為編碼序列中由si狀態轉移到sj狀態的次數；Mi為編碼序列處于si狀態的總次數.

基于式(6)可以求出馬爾科夫鏈n步的狀態轉移矩陣為

(7)

計算出轉移矩陣，則要預測r+1步的狀態.以第r步的狀態sr為依據，從狀態轉移矩陣中找到狀態sr轉移的最大概率，即max(Prl(n))，其中l=1，2，…，r，最終sl狀態則為r+1步可能性最大的狀態.

1.3 長短期記憶網絡

Hochreiter等[12]最早提出了LSTM神經網絡，其對RNN做出了改進.RNN是用于處理序列數據的神經網絡，隨著歷史信息和當前預測信息距離的增大，其喪失了從過去學習信息的能力，即梯度消失問題.而LSTM神經網絡能夠解決RNN的梯度消失問題，LSTM神經網絡標準結構如圖1所示.

LSTM神經網絡之所以能夠解決梯度消失問題，主要是引入了一個Cell處理器.在Cell中主要包含三扇門，分別為遺忘門、輸入門及輸出門[13-14].

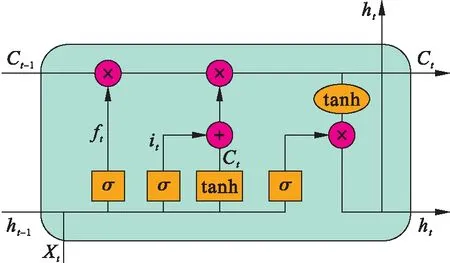
圖1 LSTM網絡結構Fig.1 LSTM network structure

遺忘門用于決定上一階段有多少信息可以傳遞到當前狀態.若輸出為0，則丟棄上一階段的全部信息；若輸出為1，則保留上一階段的信息，其篩選表達式為

ft=σ(Wf[ht-1，Xt]+bf)

(8)

式中：σ為sigmoid激活函數；Wf為遺忘門當前的輸入Xt與前一時刻輸出ht-1相乘的權重；bf為偏置.

輸入門用來決定有多少當前輸入信息可以加入記憶單元.通過sigmoid層決定更新值，通過tanh層生成當前新的記憶單元候選狀態，即

(9)

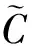
輸出門主要決定模型的輸出，其利用sigmoid函數得到初始輸出，再利用tanh函數將值縮放到(-1，1)，將兩者相乘得到輸出公式為

ht=ottanhCt

(10)

ot=σ(W0[ht-1，Xt]+b0)

(11)

函數sigmoid是不考慮之前學到的信息輸出，函數tanh則是對之前學到的信息進行壓縮，將兩者結合即為LSTM的思想.

1.4 整體模型

本文提出的整體網絡結構如圖2所示.模型主要包含3個部分，第1部分是對樓宇日用電曲線進行聚類，得到K簇并對簇編碼(0～K-1)；第2部分利用馬爾科夫鏈模型預測樓宇的用電曲線編碼，每個樓宇利用r天的用電編碼預測第r+1天的用電編碼，目的是為了得到r+1天的用電曲線原型；第3部分是對樓宇的短期負荷進行預測，將馬爾科夫鏈預測的用電編碼作為一個特征，結合歷史負荷數據，利用LSTM進行短期的負荷預測.

2 實驗過程

2.1 實驗配置

本案例研究選擇芝加哥8個樓宇2014年6月至9月工作日的用電情況，共計696條日用電曲線，用電數據獲取頻率為每小時一次.研究中涉及的所有實驗均基于python3.7編譯環境下，神經網絡模型均基于TensorFlow開發的Keras.實驗涉及的模型超參數如表1～2所示.在進行深度模型實驗時，對數據進行分割，其中60%的數據作為訓練集，20%的數據作為驗證集，其余的20%作為測試集.

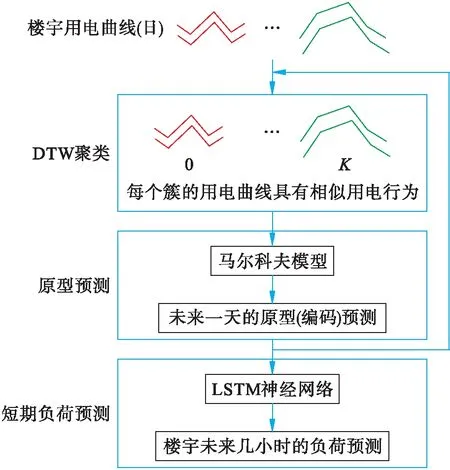
圖2 整體網絡結構Fig.2 Overall network structure

表1 SVR模型超參數Tab.1 SVR model hyper-parameters

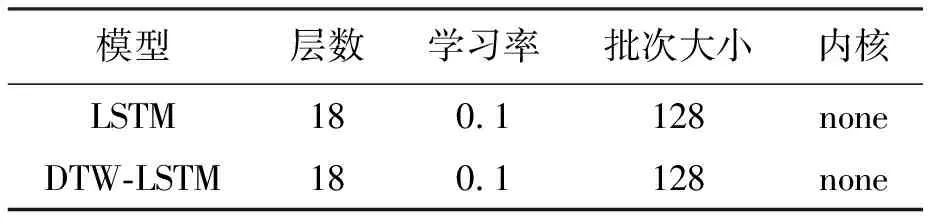
表2 深度模型超參數Tab.2 Depth model hyper-parameters

2.2 聚類實驗

2.2.1 聚類評價標準

為了評價聚類的效果，本文利用3個性能指標來進行衡量：

1) 各簇中的用電曲線與簇中心的距離之和記作WC，該指標可以評價簇的緊湊性.

2) 各簇心之間的距離之和記作WB，該指標可以評價簇之間的差異性，計算表達式為

(12)

3) WC與WB的比值記作WCBCR，該指標可以評價兩者變化的比率.一個好的聚類結果，應具有較小的WC值和WCBCR值，以及較大的WB值.

2.2.2 聚類結果

對于8個樓宇的日用電曲線數據，實驗聚類數目為5～65簇.圖3記錄了不同聚類數目的WCBCR評價指標.

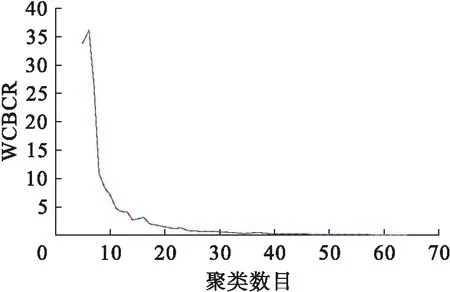
圖3 WCBCR指標Fig.3 WCBCR indicator

隨著聚類數目增多，簇之間的距離之和變大，故WB的值增大；每個簇中曲線越來越緊湊，故WC的值減小.綜合上述兩點，WCBCR的值隨著聚類數目增加逐漸減小.但在聚類數目11之前下降較快，而在聚類數目11之后下降較慢，根據拐點法選擇聚類數目為11最佳.圖4為最終的聚類結果，并對每個簇進行編碼(0～10).

2.2.3 編碼預測

對于編碼的預測，本文基于樓宇中每10天的編碼，并利用馬爾科夫鏈模型預測第11天的編碼.

對于每個樓宇，編碼預測正確率如表3所示.從表3中可以得到編碼預測平均正確率為92.19%，這為下一步負荷預測奠定了良好的基礎.

2.3 負荷預測實驗

2.3.1 預測結果評估指標

對實驗預測結果的評估指標使用絕對百分比誤差(MAPE)、平均絕對誤差(MAE)以及均方根誤差(RMSE)，其具體計算表達式為

(13)

(14)

(15)

式中：Zip為預測值；Zit為真實值.

2.3.2 負荷預測結果

1) LSTM與DTW-LSTM比較.該實驗主要是為了說明DTW聚類算法對預測結果的提升，表4分別給出了兩個模型的各參數對比情況.

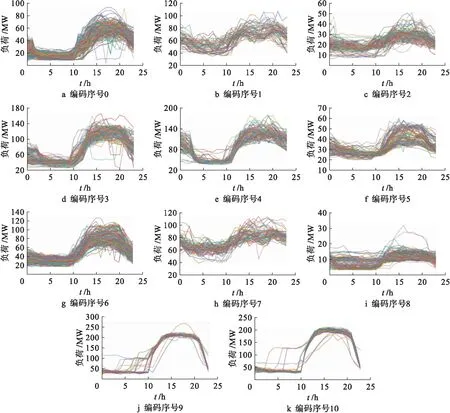
圖4 11簇聚類結果Fig.4 Clustering results of 11 clusters

表3 編碼預測正確率Tab.3 Coding forecasting accuracy

從表4中可以看出，DTW-LSTM模型對于各個樓宇的預測精度均有所提升.以MAPE指標為例，提升幅度最大值為1.325 2%，最小提升幅度為0.38%，平均提升幅度為0.861 3%.通過分析發現，8號樓中的日用電曲線的聚類結果較為分散，故編碼對負荷預測的影響較大；而1號樓中的日用電曲線聚類結果幾乎為同一個簇，編碼對負荷產生的影響較小，符合最終的結果.

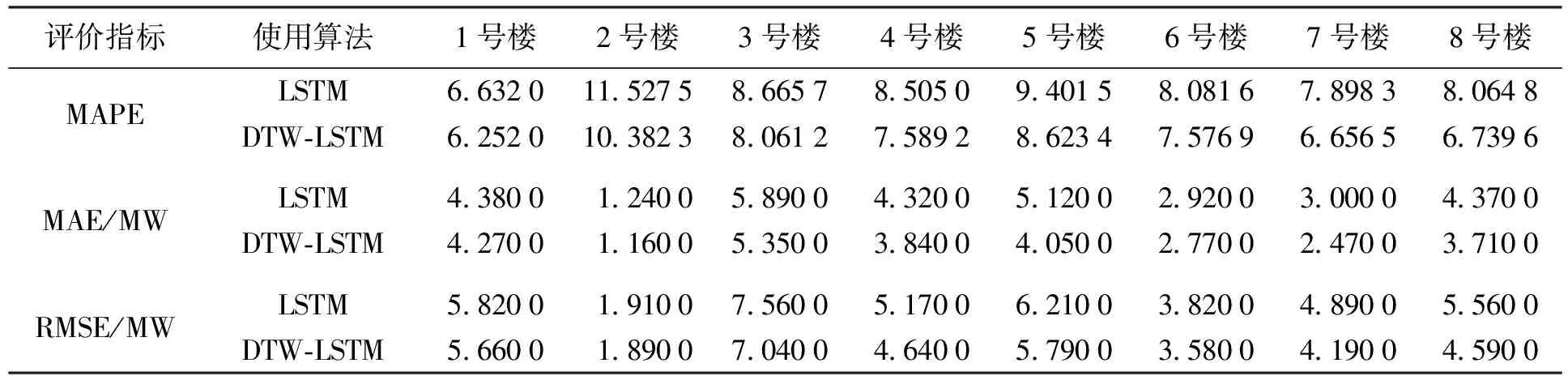
表4 MAPE、MAE和RMSE指標Tab.4 MAPE，MAE and RMSE indicators

綜上所述，DTW聚類用電原型的預測對于最終的負荷預測精度提升是有幫助的，且該模型對樓宇的負荷預測具有普適性.

2) DTW-LSTM與SVR比較.為了證明DTW-LSTM模型相對于傳統負荷預測模型的性能提升，本文選擇SVR模型進行精度對比，對比結果如表5所示.

由表5中可以發現，DTW-LSTM模型在各性能指標方面均優于SVR模型，MAPE指標平均降低1.703%，MAE指標平均降低1.056 MW，RMSE指標平均降低1.06 MW，且模型具有泛化能力，對所有的樓宇具有普適性.因此在實際的應用中，DTW-LSTM模型完全能夠勝任樓宇短期的負荷預測.

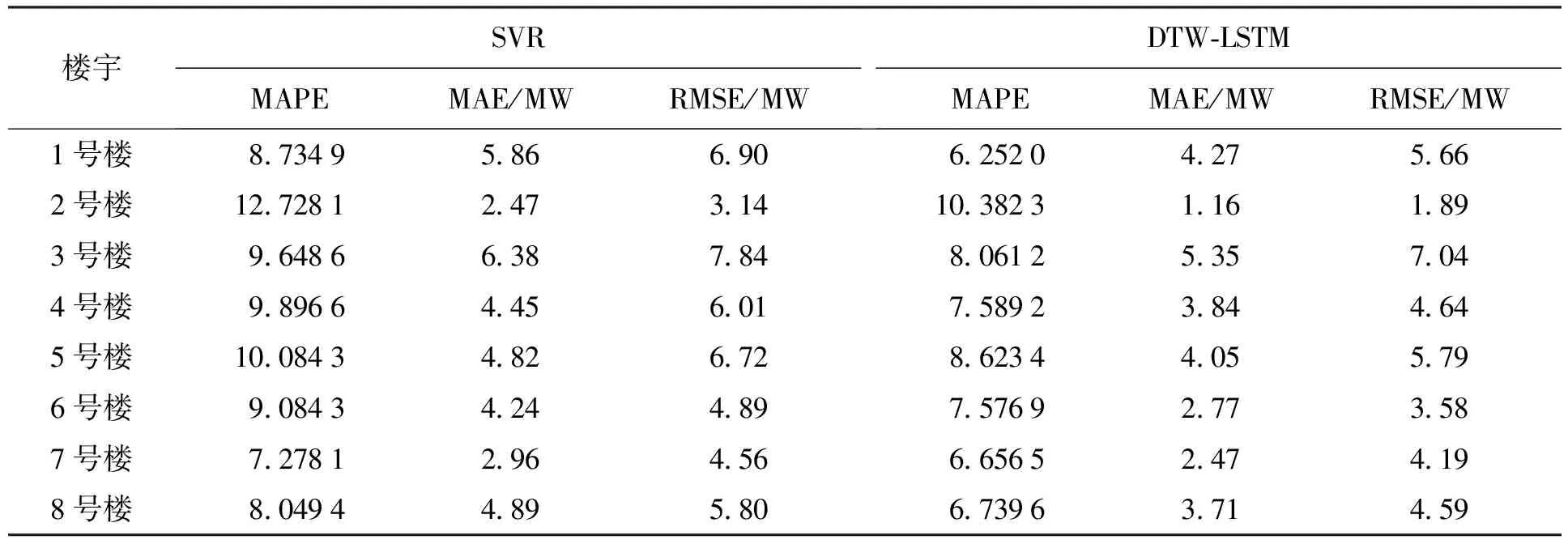
表5 性能對比結果Tab.5 Performance comparison results

3 結 論

本研究提出了DTW-LSTM短期負荷預測模型.首先與LSTM神經網絡模型進行性能對比，說明DTW聚類后預測未來的用電原型對精度的提升效果；其次與SVR模型進行系統地比較，分析其模型對比傳統算法提高的效果.實驗表明，DTW-LSTM短期負荷預測模型取得了較好的效果.

綜上所述，DTW-LSTM模型在負荷預測精度上有所提高，且該模型對樓宇具有普適性.但在此基礎上，仍可繼續研究，例如將日用電曲線進行劃分，將劃分結果進行DTW聚類，這樣的編碼會精確到以小時為單位，最終負荷預測精度仍將會有所提高.