基于Workbench的拆解平臺單側起吊過程分析

王慶豐,朱翔宇,祁 斌

(江蘇科技大學 船舶與海洋工程學院，鎮江212100)

隨著海上作業的逐步發展,遠海環境下,貨物的起重作業逐漸增多,主要集中于大型全回轉起重船和起重平臺．針對起重作業下,國內外學者對船體、平臺等的浮態變化及吊物的運動情況進行了大量研究．文獻[1]對小波高、長周期涌浪環境下起重船耦合系統運動響應特性及其機理開展了參數敏感性分析．文獻[2-3]通過模型試驗的手段對起重船系統運動響應及其機理進行研究．通過數值模擬方法對全回轉起重船吊物及船體運動響應情況進行了研究．文獻[4]利用Lingo軟件對全回轉起重船算例進行計算．文獻[5]以起重能力1 600 t的起重船為研究對象,采用物理模型試驗方法給出了起重船施工作業的波浪條件．文獻[6-7]對平臺上部模塊進行了數值分析．文獻[8-10]對半潛平臺起重船的性能及浮吊系統進行研究．文獻[11-14]對海上起重船響應進行研究．文獻[15]對近島礁浮式平臺的運動響應進行了研究．文獻[16]對自升式平臺碼頭系泊斷裂進行了研究．

文中采用Workbench Aqwa軟件對某一非對稱拆解平臺進行吊重模擬,通過絞機收縮纜繩的方式模擬拆解平臺對吊物的起吊過程．通過對數值分析的結果進行研究,得出拆解平臺單側起吊的作業規律以及長時間恒定吊載下平臺的穩性變化情況．

1 計算理論

1.1 時域耦合理論

根據Cummins脈沖響應方法,船體在某一時刻的運動可以歸為一系列瞬時脈沖運動的疊加,同時將波浪力分解為一系列脈沖響應的組合,由此可以將頻域和時域計算聯系起來,使得時域計算過程可以應用頻率的計算結果．時域分析中運動方程為:

F(1)(t)+F(2)(t)+Fc+Fw+Fb(t)+

Ft(t)+Fe(t)

(1)

式中：M為船體質量矩陣；A為流體附加質量矩陣；C為阻尼矩陣；K為結構總體剛度系數；h(t)為加速度脈沖函數；F(1)(t)為一階波浪力；F(2)(t)為二階波浪力；Fc為流阻力；Fw為風阻力；Fb(t)為非線性舭部橫搖阻尼力；Ft(t)為系泊纜載荷；F(e)(t)為船體可能受到的如撞擊力等其他外力．

(2)

式中，A(ω)、B(ω)分別為頻域計算中波浪頻率為ω時的附加質量與阻尼系數．

1.2 系泊纜動力分析

對于系泊狀態下的船舶,船體與系泊纜之間會相互影響,考慮二者之間的耦合作用能提高計算的可靠性．計入動態分析后,需要考慮系泊纜的質量、阻力、彈性張力和彎矩,可采用將系泊纜沿長度方向離散,將質量,系泊纜內力及外力集中于端點的方法計算系泊纜動態響應．

系泊纜單元的受力方程為:

(3)

式中:m為系泊纜單位長度質量;q為單位長度上分布的力矩載荷矢量;R為系泊纜單元第一個點的位置矢量;Se為系泊纜單元長度;w為系泊纜單元質量;Fh為系泊纜單元單位長度的水動力矢量;T為系泊纜單元第一個點的張力矢量;M為系泊纜單元第一個點的彎矩矢量;V為系泊纜單元第一個點的剪切力矢量．

彎矩和張力與材料的抗彎剛度EI和軸向剛度EA有關:

(4)

式中，ε為系泊纜單元的軸向應變．

2 計算模型

2.1 水動力模型

以一非對稱無橫撐的半潛式拆解平臺為研究對象,該平臺于150 m水深的海域內進行起重作業．平臺主尺度如表1.

表1 主尺度表Table 1 Principal scale table m

該平臺在進行起吊作業時,采用十字錨泊系泊方式．平臺使用4×2的懸鏈式系泊布置,主浮筒船首船艉左舷側各兩條系泊纜,副浮筒船首船艉右舷各兩條系泊纜．系泊纜布置方式隨吃水深度及環境載荷的變化而發生變化．坐標系以平臺尾部至艏部方向為x軸正方向,平臺中心為原點．以主浮筒外側為y軸正方向,主浮筒中心為原點,水線面以上為z軸正方向．水動力模型如圖1,系泊布置如圖2．

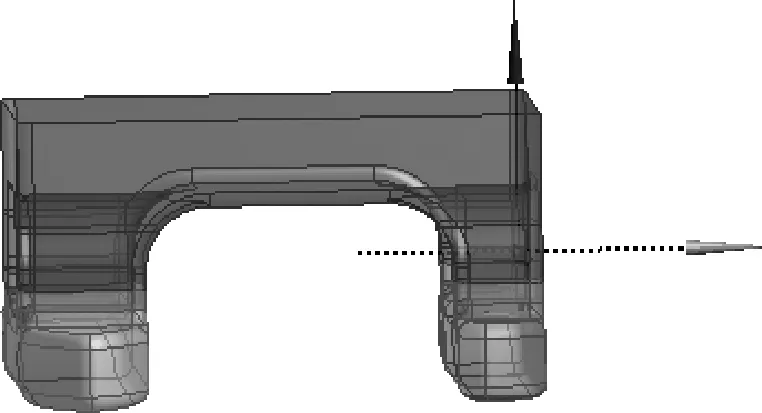
圖1 水動力模型Fig.1 Hydrodynamic model

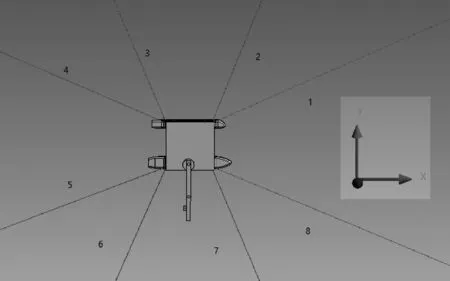
圖2 系泊布置Fig.2 Mooring layout

文中依據平臺資料,建立水動力模型,通過Aqwa的Hydrodynamic Diffraction模塊計算分析得到海洋平臺的水動力系數．

由圖3、4可以看出橫搖和縱搖的最大值均發生在10～15 s的周期內,分別出現在浪向角α為90°、180°的情況下,在設定環境載荷參數時,應避免設置此類波浪周期．

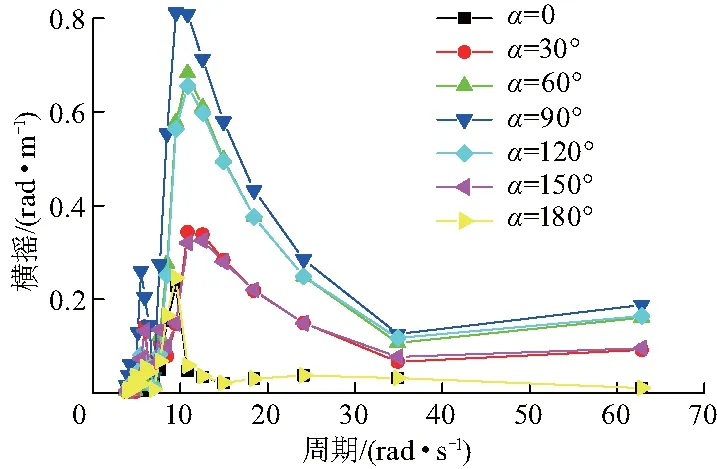
圖3 拆解平臺橫搖傳遞函數Fig.3 Roll transfer function of platform

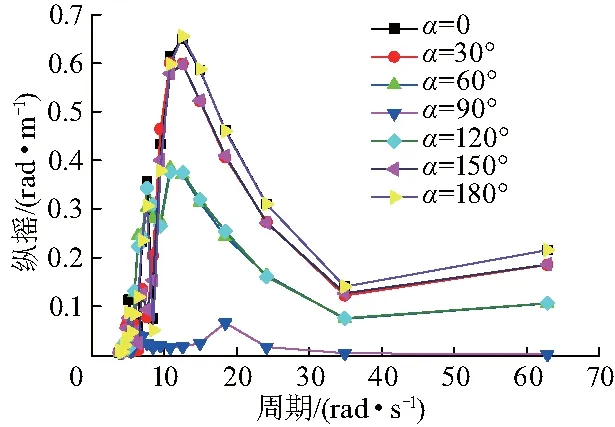
圖4 拆解平臺縱搖傳遞函數Fig.4 Pitch transfer function of platform

2.2 環境載荷設置

環境載荷1條件如表2，不規則波譜為JONSWAP譜，如圖5．

表2 計算環境載荷1Table 2 Environmental condition

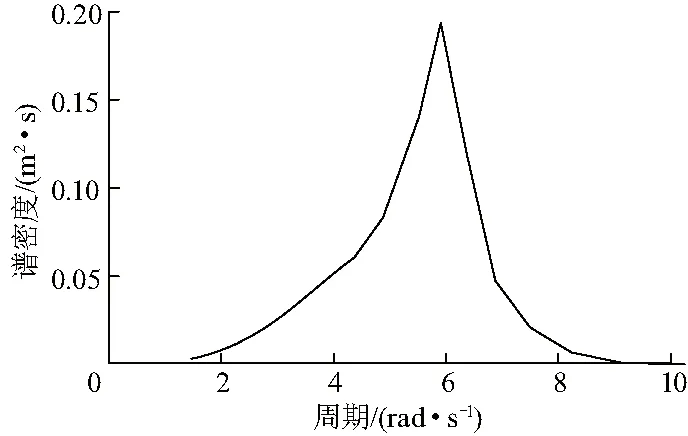
圖5 不規則波波譜Fig.5 Irregular wave spectrum

不規則波的方向設置為0,風速為15 m/s,流速為1 m/s,環境載荷入射角都設置為0．

3 計算結果及分析

3.1 不同吊臂旋轉角下平臺與吊物的運動響應

拆解平臺選用主浮筒一側進行起吊過程模擬,吊臂旋轉角β為15°～165°．吊物起吊采用四點起吊布置,通過cable winch操作使得四條起吊纜繩受力一致．吊物自重約為3 000 kg,長為5 m,寬為2 m,每條起吊纜繩受力為8 000 N,環境載荷選用計算環境載荷1,吊物自水下1 m起吊至12 m高處,平臺起吊模擬如圖6,吊物自身運動響應最值及平臺運動響應最值如表3.

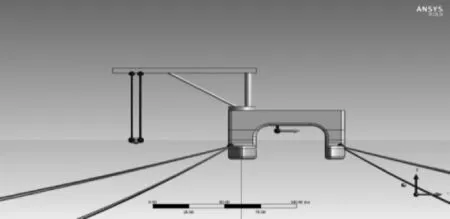
圖6 平臺起吊示意Fig.6 Schematic diagram of platform lifting

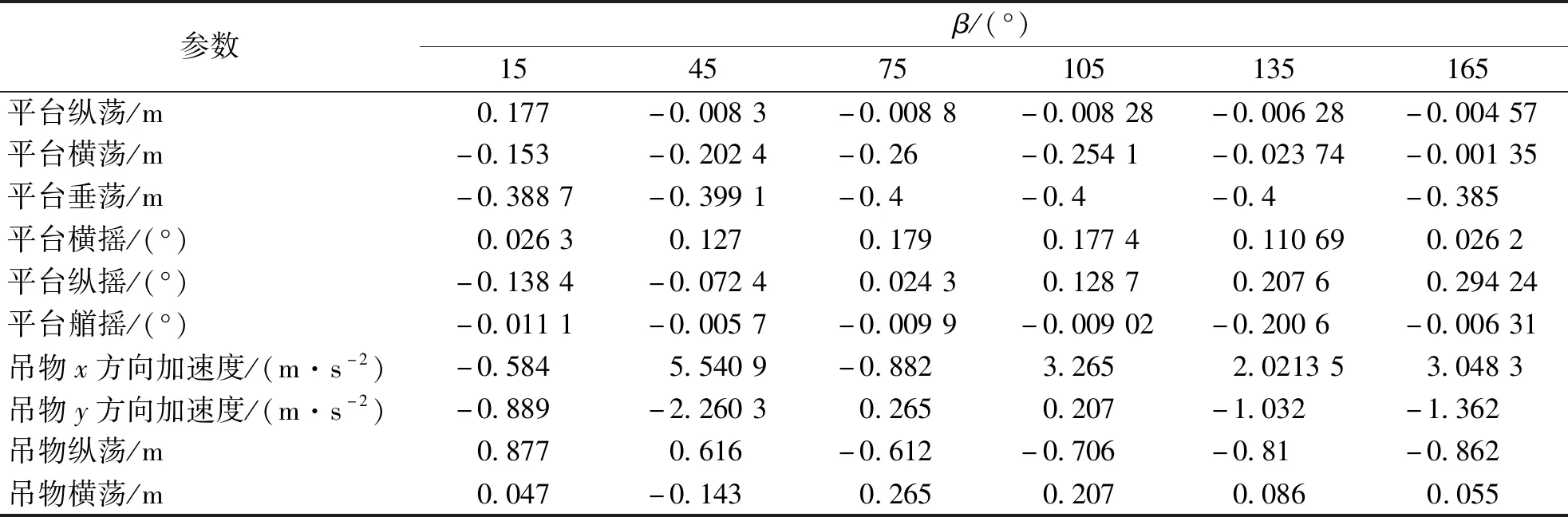
表3 起吊過程中平臺吊物的運動響應Table 3 Motion response of platform crane during lifting

平臺總體運動響應變化較小,由表3可知,除15°吊臂旋轉角以外,平臺縱蕩數值均在0.1以下,而平臺縱蕩的數值分布與吊物縱蕩數值分布趨勢相同,當吊臂旋轉角β為15°時,吊物縱蕩達到最大值．平臺垂蕩在-0.4 m左右浮動,其中75°～135°下平臺垂蕩基本保持不變．平臺橫蕩均小于0.27 m,當吊臂旋轉角由15°～75°增加時,平臺橫蕩增加,由75°～165°減小時,平臺橫蕩減小．75°時的吊物運動響應曲線如圖7～10.

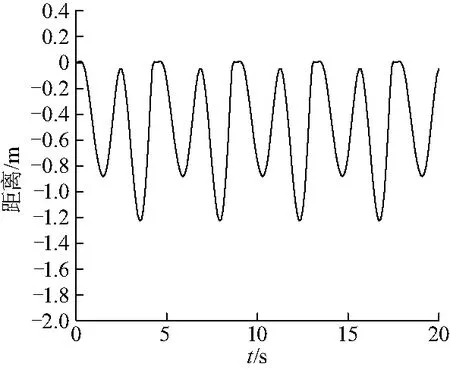
圖7 75°時吊物縱蕩運動曲線Fig.7 Surge motion curve of crane at 75°

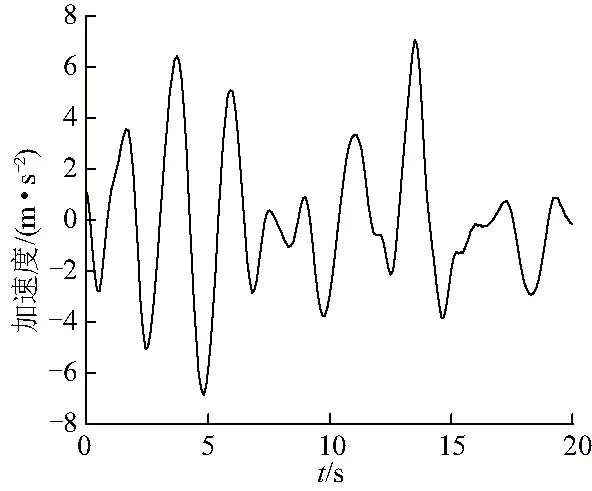
圖8 75°時吊物縱向加速度運動曲線Fig.8 Vertical acceleration curve of crane at 75°

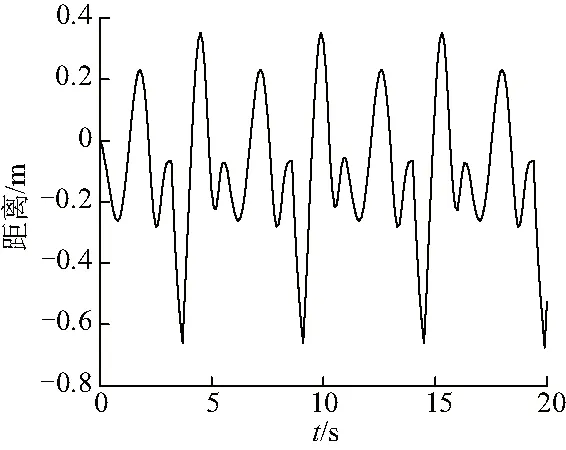
圖9 75°時吊物橫蕩運動曲線Fig.9 Swing motion curve of crane at 75°

圖10 75°時吊物橫向加速度運動曲線Fig.10 Transverse acceleration curve of crane at 75°

取表3中吊物橫蕩與縱蕩運動幅值的絕對值作柱狀圖(圖11、12),分析吊臂旋轉角β對吊物運動幅度的影響.

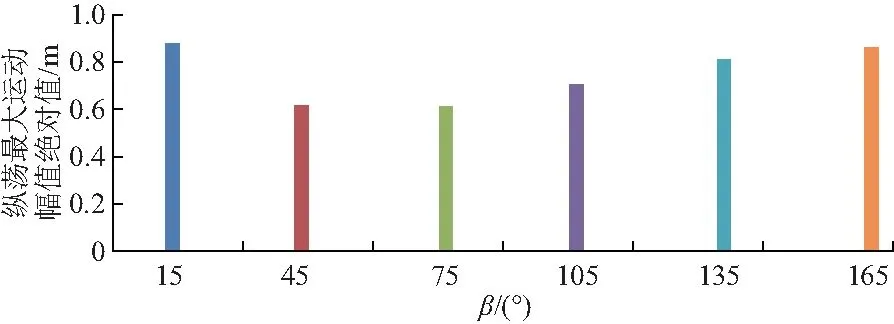
圖11 吊物縱蕩運動幅度對比Fig.11 Comparing diagram of surge motion amplitude of lifting object

由圖11可知,吊物縱蕩運動幅值的絕對值隨吊臂旋轉角整體上呈現先減少后增加的趨勢,該趨勢與平臺的縱蕩趨勢基本一致．圖12中最低點為吊臂旋轉角為75°時,此時縱向加速度呈無序狀態,說明吊臂旋轉角對于吊物縱向運動影響較小．

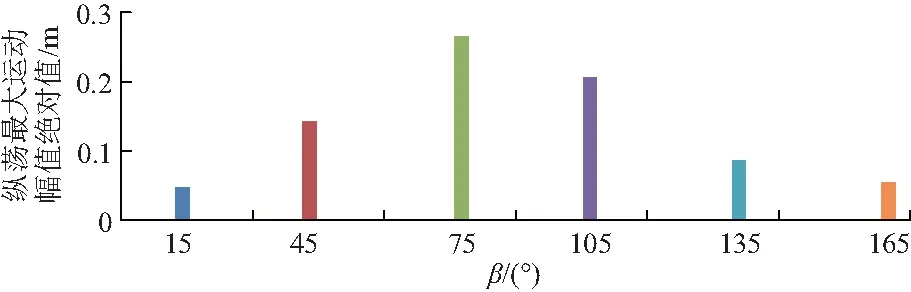
圖12 吊物橫蕩運動幅度對比Fig.12 Comparing diagram of sway motion amplitude of lifting object

由圖12可知,吊物橫蕩運動幅值絕對值隨吊臂旋轉角的增加而呈現先增加后減少的趨勢,該運動趨勢與平臺的橫蕩運動趨勢基本一致．因此起吊過程中,吊臂旋轉角增加到75°時對平臺縱蕩有一定抑制作用,對平臺橫蕩則有一定的加強作用．

3.2 不同懸臂角下吊物恒處于一定高度時,平臺運動響應

由于Workbench軟件不支持吊物恒定于一定高度的數值模擬,因此以固定載荷作為替代,不再考慮吊物的運動響應,重點考慮平臺運動響應．

此時將3 000 kg的吊物替換為30 000 N的外加載荷．拆解平臺仍采用同樣的系泊布置,起重機位于主浮筒一側,以平臺船艏為0,沿逆時針方向,每隔15°為一個工況將360°的作業工況劃分為24個作業工況以進行計算．采用上文的環境載荷工況1進行計算．計算載荷1為一般作業工況,礙于篇幅所限從中選出0、60°、90°、120°、180°、-60°、-90°、-120°這8個變化較為明顯的情形進行分析．

環境載荷1下吊臂角下平臺運動響應時歷與系泊纜時歷曲線如圖13、14,匯總結果如表4．

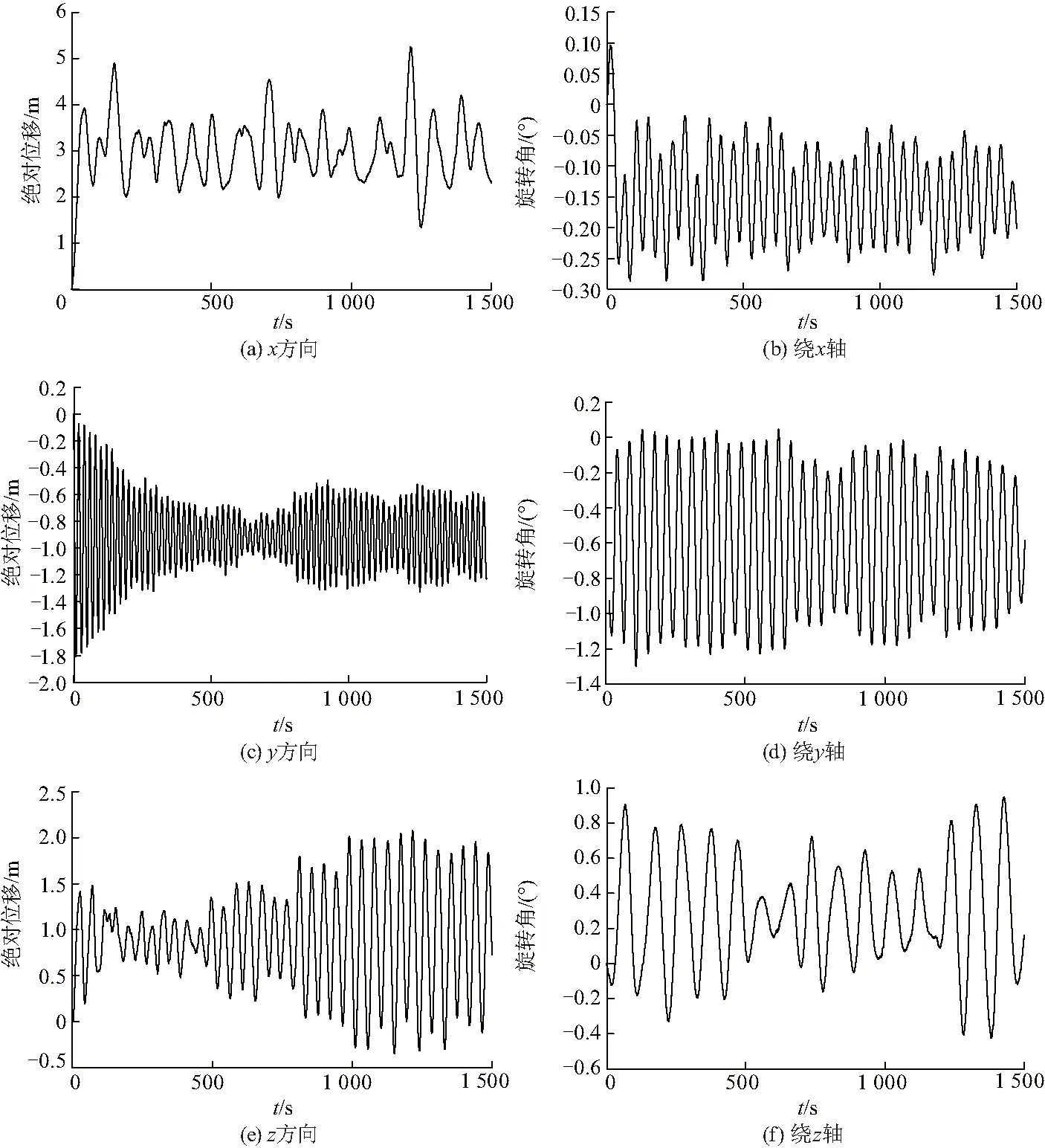
圖13 平臺六自由度運動響應曲線Fig.13 6-DOF motion response curve of platform

從表4中可以看出平臺的橫搖變化比較明顯,吊臂的旋轉角β從0變化至90°期間,船體的橫搖角逐漸變大,之后隨著吊臂旋轉角度繼續增大,平臺橫搖角逐漸減小．縱搖在180°時達到最小,且正負方向運動響應幅值不同．平臺縱蕩由0趨近180°時減小,并在180°時達到最小．橫蕩位移受吊臂方向影響在90°時達到最大,而升沉運動全程不受吊臂旋轉角的影響,縱蕩橫蕩升沉運動正負方向運動幅值完全一致．

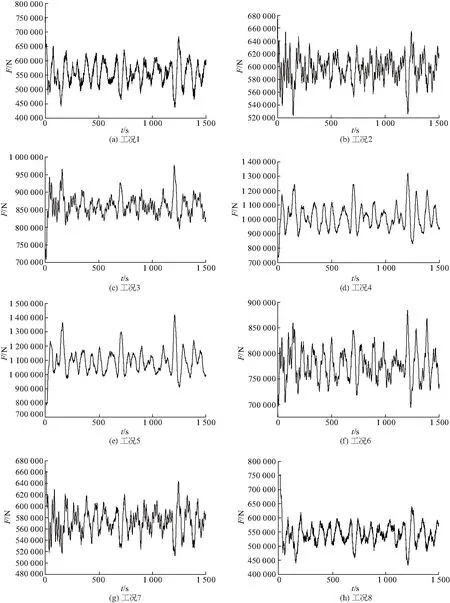
圖14 平臺系泊纜拉力F曲線Fig.14 Pull curve of platform mooring line

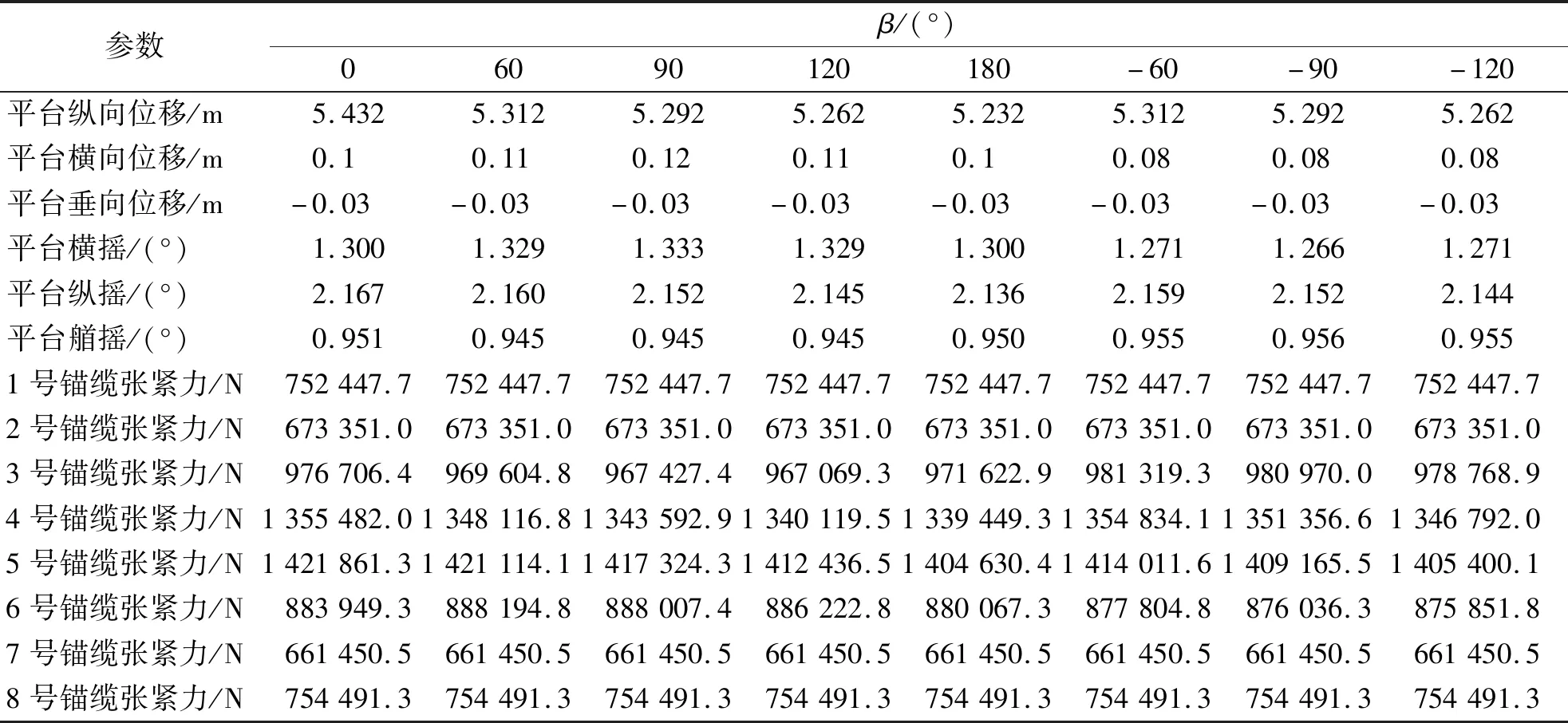
表4 吊重在環境載荷1入射角0計算結果最大值匯總Table 4 Maximum value summary of calculation results when condition1 ais 0

系泊纜的張緊力則隨著吊臂旋轉角的逐漸改變發生改變,其中4、5號錨纜所受張緊力最大,由于風流載荷入射角為0,與4、5號錨纜呈對向,因此受力最大,也是斷裂最可能發生的地方．當由0轉向180°的過程中4、5號錨纜張緊力隨角度增加而下降,并于180°達到錨纜張緊力的最小值,對應縱蕩的最小值．1、8號錨鏈受風流載荷為順向,因此在吊臂方向改變時無變化,說明3 000 kg載重情況下,風流載荷的對向錨纜受吊臂伸出角度影響最大．

3.3 大吊載下平臺運動響應分析

平臺運動響應所添加的吊載為30 000 N,而實際作業中平臺的吊載可以達到1 500 000 N左右,以1 500 000 N的吊載作為附加載荷,環境載荷及系泊布置的設置同上,將變化趨勢較為明顯的0、60°、90°、120°、180°、-60°、-90°、-120° 8個工況的計算結果進行匯總,如表5.

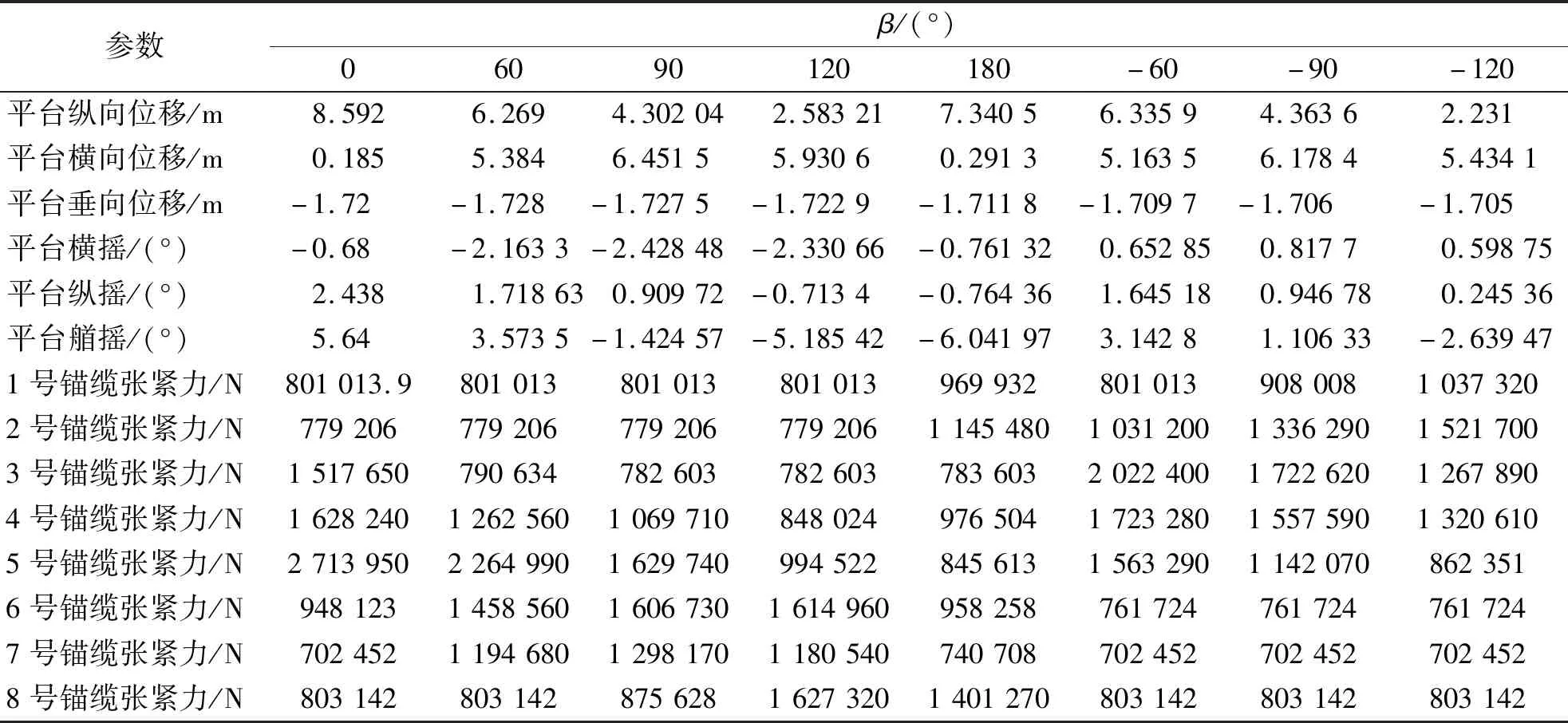
表5 吊重在環境載荷1入射角0計算結果最大值匯總Table 5 Maximum value summary of calculation results when cindition1 ais 0

由表5可以發現,垂蕩位移較之于表4,吃水深度發生了明顯增加,由60°至-180°、-60°至-120°的β變化中,吃水深度逐漸減小,吃水最小值發生在-120°．在表4所對應工況下,β值改變,橫蕩及橫搖數值改變較小,而在較重吊載情況下,吊載方向及β值對平臺運動自由度數值影響巨大．以β值為0和90°時為例,其對應的橫蕩橫搖數值分別為0.185 m、-0.68°以及6.45 m、-2.42°,數值變化幅度在4倍以上．由表5中縱蕩數值的變化可以看出,當吊載增加時,β越接近90°,縱蕩抑制現象越明顯,即圖中60°、90°、120°、-60°、-90°、-120°所示．

大吊載下,4、5號系泊纜受力趨勢與表4基本一致．與表4中其余系泊纜受力無明顯變化不同,表5中除4、5號系泊纜外,其余6根系泊纜受力均出現明顯變化,1～4號系泊纜在-60°、-90°、-120°吊臂旋轉角時的受力均遠超過90°與120°吊臂旋轉角時系泊纜的受力,由圖2可知,這4根系泊纜均布置在拆解平臺的副浮筒方向,由于吊機位于主浮筒一側,此時力矩較長,系泊纜受力較大．同樣,當吊臂旋轉角位于主浮筒一側時,5～8號系泊纜在-60°、-90°、-120°時受力較大．其中系泊纜受力的最大值發生在β角為0時,30°β下受力也較大,應當避免0、30°下進行長時間恒定吊載．

此時將表5的中縱傾角與橫傾角整理為傾角——吊臂旋轉角的折線，如圖15、16.

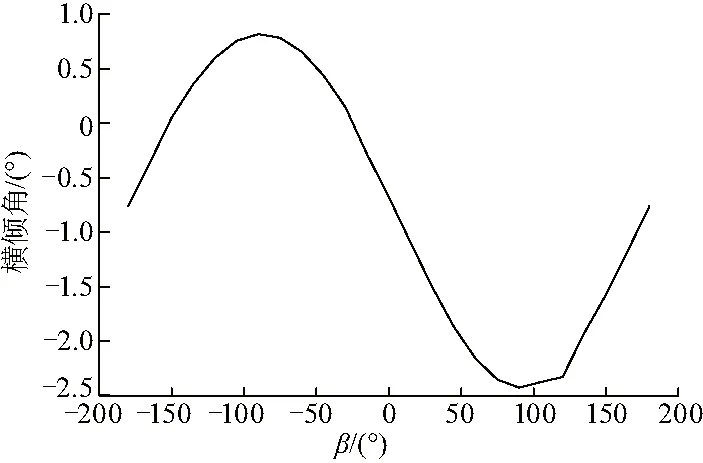
圖15 橫傾角隨β變化情況Fig.15 Change of roll angle with β

圖16 縱傾角隨β的變化情況Fig.16 Change of trim angle with β

橫傾角的最大值為2.5°,發生在β為90°時,縱傾角的最大值為2.3°發生在β為0時．除去圖15、16中的極值情況,縱傾角的變化幅值小于橫傾角．因此,拆解平臺單側吊機起重作業時應當重點注意橫傾角的變化．根據CCS的起重平臺浮態穩性標準,橫傾角應當小于5°,縱傾角應當小于2.5°．因此在1 500 000 N載荷下平臺起重穩性保持在安全范圍內．

4 結論

(1)進行單側起吊時,吊物縱蕩運動幅值的絕對值隨吊臂旋轉角增加整體上呈現先減少后增加的趨勢,橫蕩運動幅值絕對值隨吊臂旋轉角的增加而呈現先增加后減少的趨勢,吊物的運動趨勢與平臺運動趨勢保持一致．吊臂旋轉角增加到75°時對平臺縱蕩有一定抑制作用,對平臺橫蕩有一定的加強作用．

(2)在添加30 000 N吊載的情況下,平臺的最大受力系泊纜為4、5號系泊纜,均為風流載荷的對向系泊纜．吊臂的旋轉角從0變化至90°期間,船體的橫搖角逐漸變大,之后隨著吊臂旋轉角度的增大船體橫搖角逐漸減小．縱搖在180°時達到最小,且正負方向運動響應幅值不同．平臺縱蕩由0趨近180°時減小,并在180°時達到最小．橫蕩位移受吊臂方向影響在90°時達到最大,而升沉運動全程不受吊臂旋轉角的影響,縱蕩橫蕩升沉運動正負方向運動幅值完全一致．

(3)添加了1 500 000 N吊載后,吊臂旋轉角角度對船體自由度影響巨大,超過環境載荷入射角對平臺運動的影響,仍存在著對縱蕩運動的抑制作用．吊臂旋轉角為0、30°、90°時,平臺的運動響應較大,應當避免此工況下進行起吊作業．

(4)對360°工況下的平臺起吊作業進行數值模擬,結果表明拆解平臺在較大載荷即1 500 000 N的情況下,仍符合CCS的穩性要求,就實際作業中的平臺穩性變化情況,為工程人員提供參考．