氣墊船典型結構振動特性分析

諸葛凌波，劉 寧，唐首祺

(1.中國船舶及海洋工程設計研究院，上海 200011；2.哈爾濱工程大學船舶工程學院，黑龍江 哈爾濱 150001)

0 引 言

中國船級社《海上高速船入級及建造規范》[1]中對氣墊船的定義如下：系指船舶不論在靜止或運動時，其全部重量或大部分重量能被連續產生的氣墊所支承的船舶。氣墊船在航行過程中就猶如在船體與水面之間加入了一個流動的空氣層，減小了水對船體的阻力，從而使船可以在水面上高速行駛或者在海灘等界面登陸，可使航速高達60～80 km/h，可以完成多種使命，在軍用和民用領域都有著十分廣闊的發展潛力和應用前景，尤其適用于登陸作戰中作為登陸輸送工具使用。

由于氣墊船任務使命的特殊性，使得其對自身重量的控制較常規船嚴格，這就要求其結構尺寸不能過大，也就使得船體剛度較常規船型弱，再加上高轉速發動機、高轉速空氣螺旋槳等高速振動源的作用，氣墊船激勵頻率與激勵幅值較常規船型大，使得氣墊船的振動問題更為突出。在航行中產生劇烈的振動不僅會影響舒適性和工作效率，而且較高的振動幅值和頻率更易在應力過大部位產生疲勞破壞，從而影響結構的強度和航行安全[2]。因此準確計算預報氣墊船的振動性能尤其重要。但通常計算方法只考慮單一激振力下的響應[3]，之后結合《艦船通用規范》[4]等相關規范要求進行校核，這與實際情況并不完全相符。本文采用有限元建模軟件MSC.Patran 對氣墊船進行有限元建模，考慮多種激振力在同一位置處的瞬態響應，運用MSC.Nastran 進行瞬態計算分析得到速度時歷，根據GB/T 16 301-2008 規范[5]得到振動速度的均方根值，更符合實際情況且與實測值具有可比性。

1 氣墊船振動分析

1.1 氣墊船結構振動特性分析

氣墊船的甲板面相對而言較為廣闊，同時具有較大艙室空間，氣墊船內部大體為鋁合金材質的箱體作為支撐結構，其設有燃油艙、淡水艙、舷側氣道、裝載甲板等結構，鋁合金的箱體四周為柔性圍裙，氣墊位于船底，一般采用穩定圍裙將氣墊分為不同的氣室。甲板上方安裝布置有空氣螺旋槳等，船體左右兩側或左中右分別設有墊升風機。

氣墊船在墊升狀態高速航行時，船體與水面脫離，氣墊的橡膠面與水面的接觸勢必會帶來強烈的氣墊-波浪之間的砰擊作用，造成船體結構的劇烈振動。氣墊船的激勵源很多，船上的推進主機、墊升主機、墊升風扇以及空氣螺旋槳等振動源都會產生不同頻率的激勵，再加上氣墊受波浪砰擊產生的振動，以及各種軸系傳導力的過程中會產生不同程度的振動，諸多因素使得氣墊船的振動非常復雜[6]。而氣墊船由于質量要求，通常采用較薄的鋁合金材料，使得結構本身振動頻率不高，諸多振動源會使得船體結構產生較大的結構動靜應力。所以氣墊船的振動，成為氣墊船在設計和建造過程中不能忽視的問題。

1.2 氣墊船振動源參數

結合氣墊船運行及工作原理，船上高頻振動源主要包括推進主機、空氣螺旋槳、推進主機、風機等[7]，本文選取墊升主機基座和推進主機基座這一典型結構進行振動特性分析計算，對其影響較大的激振源有推進主機（3 個）、空氣螺旋槳（3 個）、墊升主機（2 個）。由于風機離基座較遠對基座響應值影響小，所以計算時不予考慮。振動源的組成、質量、偏心距等參數如表1 所示。

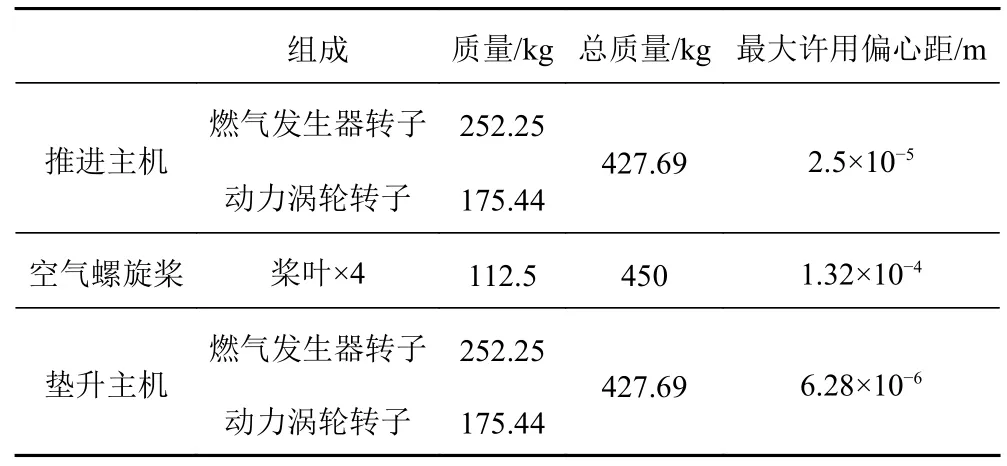
表1 振動源基本參數Tab.1 Basic parameters of vibration sources

不同頻率下的轉子動量可由下式計算：

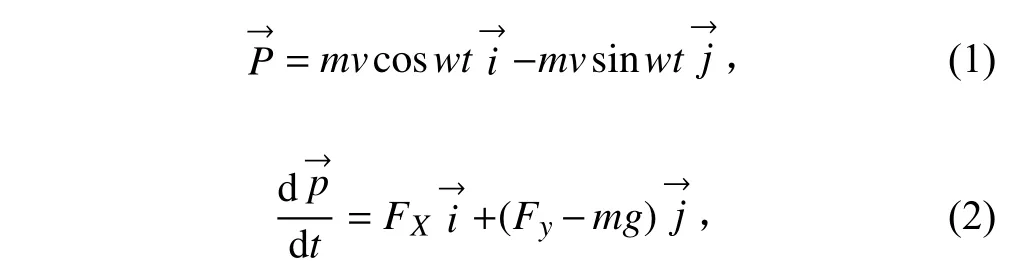
在得到轉子動量之后，可根據下式計算轉子動態激振力幅值：

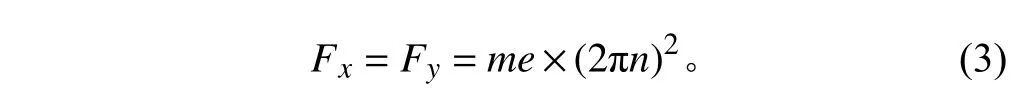
振動源在測試時激勵源頻率如表2 所示。

表2 振動源在測試時激勵源頻率Tab.2 Excitation frequency of vibration sources in test

2 氣墊船局部響應計算模型和分析區域

2.1 有限元分析計算模型

氣墊船的振動計算有限元模型依據詳細設計圖紙來建模，前后處理及分析運算均運用大型商用有限元軟件MSC/Patran和Nastran 來完成。

根據CCS《船上振動控制指南》[7]的相關規定，在計算船舶局部結構的振動問題時，梁、板、板架等并不能作為孤立結構，對于短艙內部結構，依照推進主機基座和墊升主機基座的結構圖紙對主機基座進行有限元建模，在推進主機重心位置建立MPC 點并與推進主機基座相連，將推進主機重量施加到MPC 點上。對于其他設備，如甲板上布置的空氣螺旋槳槳葉、空氣螺旋槳的槳軸等其他結構均在其重心位置建立MPC 并施加對應的重量；在墊升主機重心位置建立MPC 點與墊升主機基座相關聯，將墊升主機重量施加到MPC 點上，對于其他設備（空氣螺旋槳、槳塔、推進主機等）均在其重心位置進行配重，以達到與實船重量分布相同，將上述設備按照重心位置進行配載，使槳塔與發動機短艙結構有限元模型的重心位置與實船的重心位置一致。

計算基座處的局部響應，模型范圍取為31 剖面～船尾（約1/2 船長），這樣在保證計算精度的同時節約計算時間，而且模擬了墊升主機及推進主機的基座的邊界條件，消除了由于邊界條件設置不準確使得計算結果失真。根據文獻[8–9]邊界條件在31 剖面處取為簡支。該計算模型包括127 119 個單元，62 000 個節點。計算模型如圖1 所示。

圖1 氣墊船局部振動有限元模型Fig.1 Finite element model of local vibration of hovercraft

2.2 實船測試測點布置

為有效地研究氣墊船基座的振動問題，針對實船進行振動測試試驗，試驗振動頻率響應的測試區域選為墊升主機基座和推進主機基座，與有限元分析位置相同，即左舷推進主機和墊升主機的基座處，實船測點布置位置如圖2 所示。H1，H2，H5，H6 測點分別對應的有限元模型節點編號為Node173275，173 316，1 063 297，1 063 185。

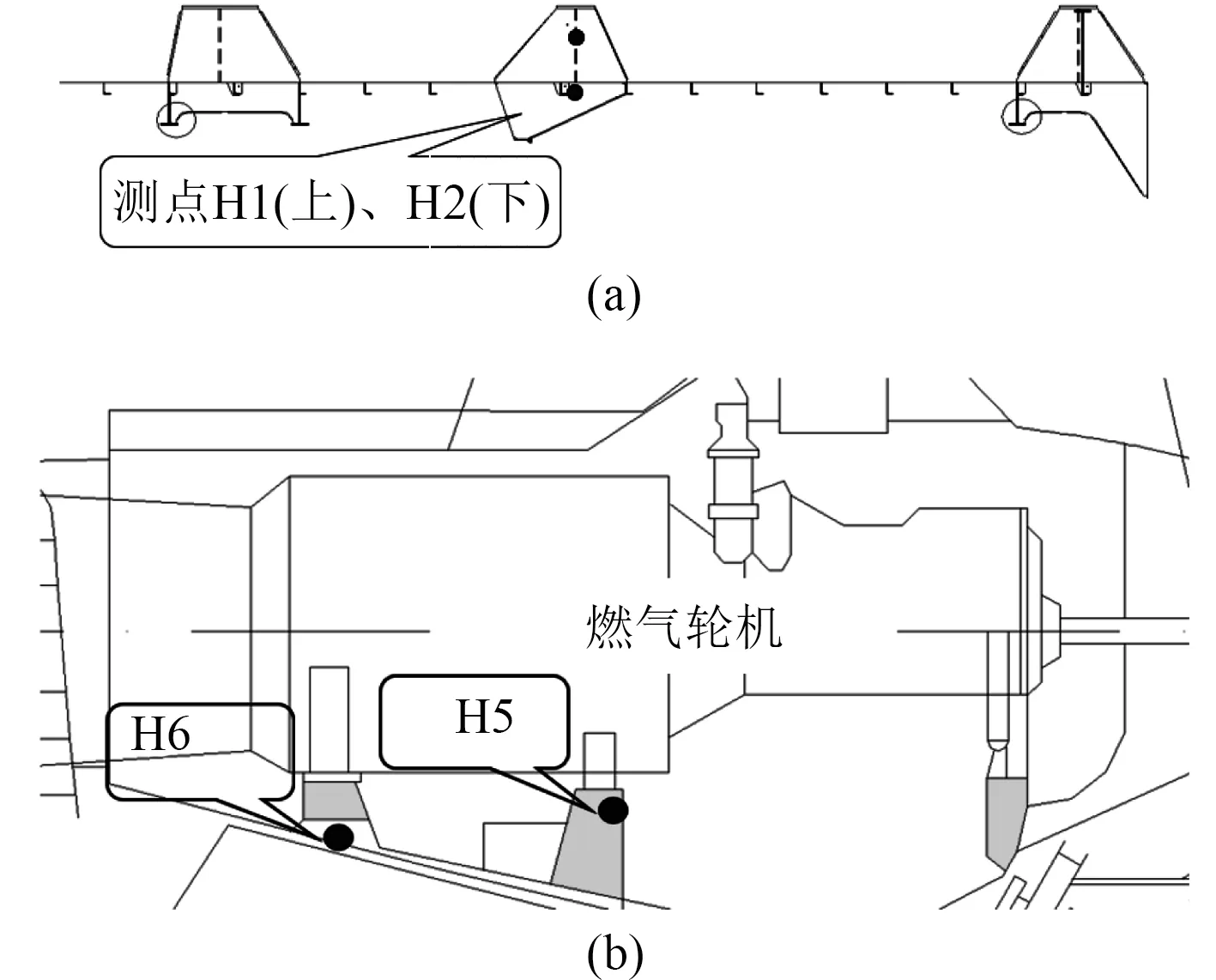
圖2 氣墊船局部振動測點布置Fig.2 Arrangement of local vibration measuring points for hovercraft

3 氣墊船局部振動響應計算及結果

3.1 局部振動分析及計算結果

考慮到測試時氣墊船處于穩定航行狀態，激振力的頻率和大小不變，激振力方向隨時間不斷變化，因此采用瞬態響應分析計算氣墊船的局部響應。建立各激振力隨時間變化的場函數，得到方向隨時間不斷變化的激振力，施加到模型上。阻尼根據經驗取0.05，時間步長取為0.001 s，步數3 100 步。

根據上述要求，在有限元模型上施加激振力的場函數并遞交計算，基座上4 個測點的加速度、速度時歷曲線部分結果如圖3～圖10 所示。

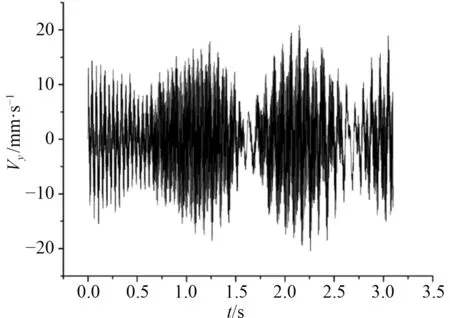
圖3 H1 點處橫向速度響應曲線Fig.3 Lateral velocity response curve at H1 point

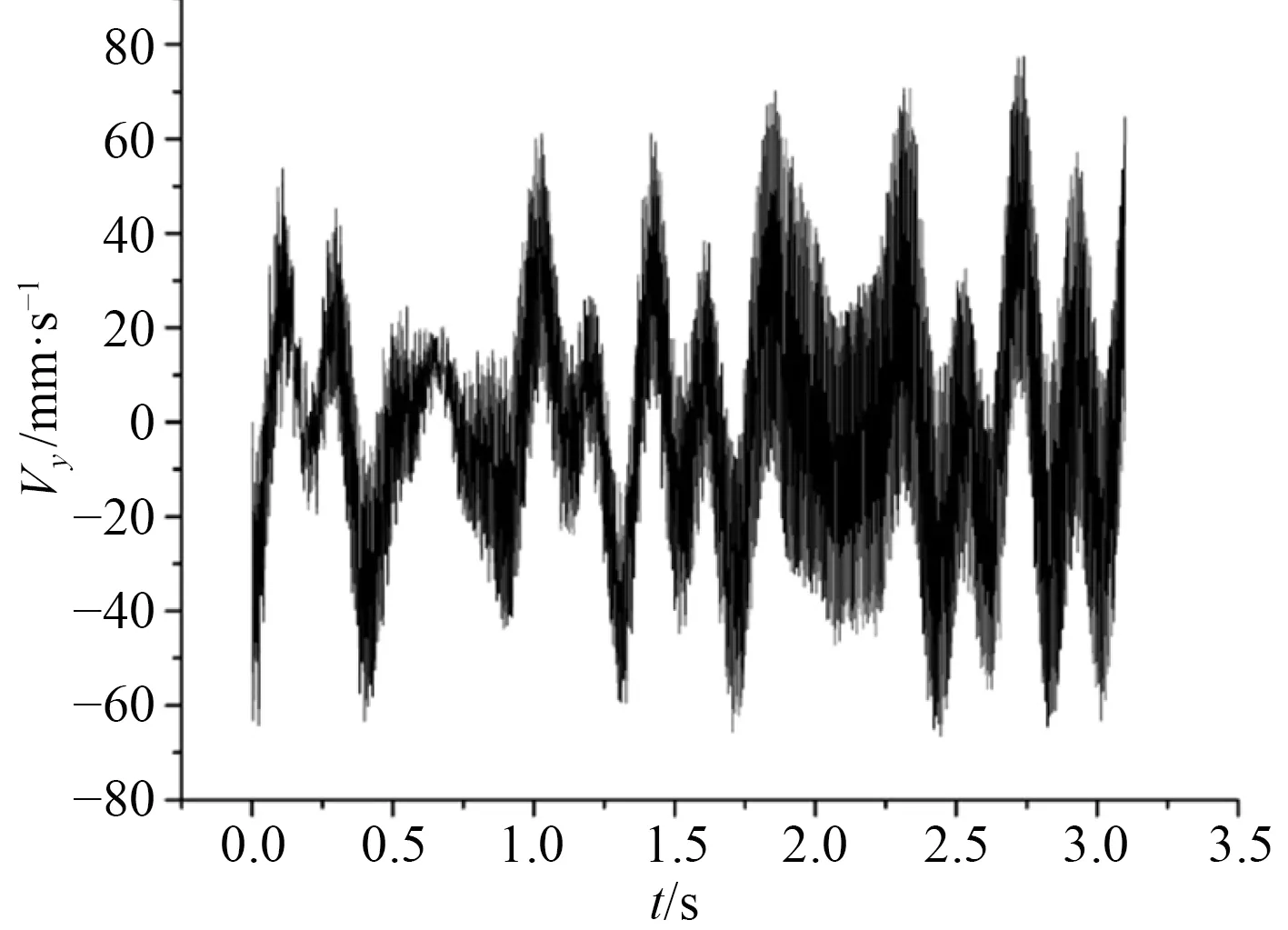
圖4 H5 點處橫向速度響應曲線Fig.4 Lateral velocity response curve at H5 point

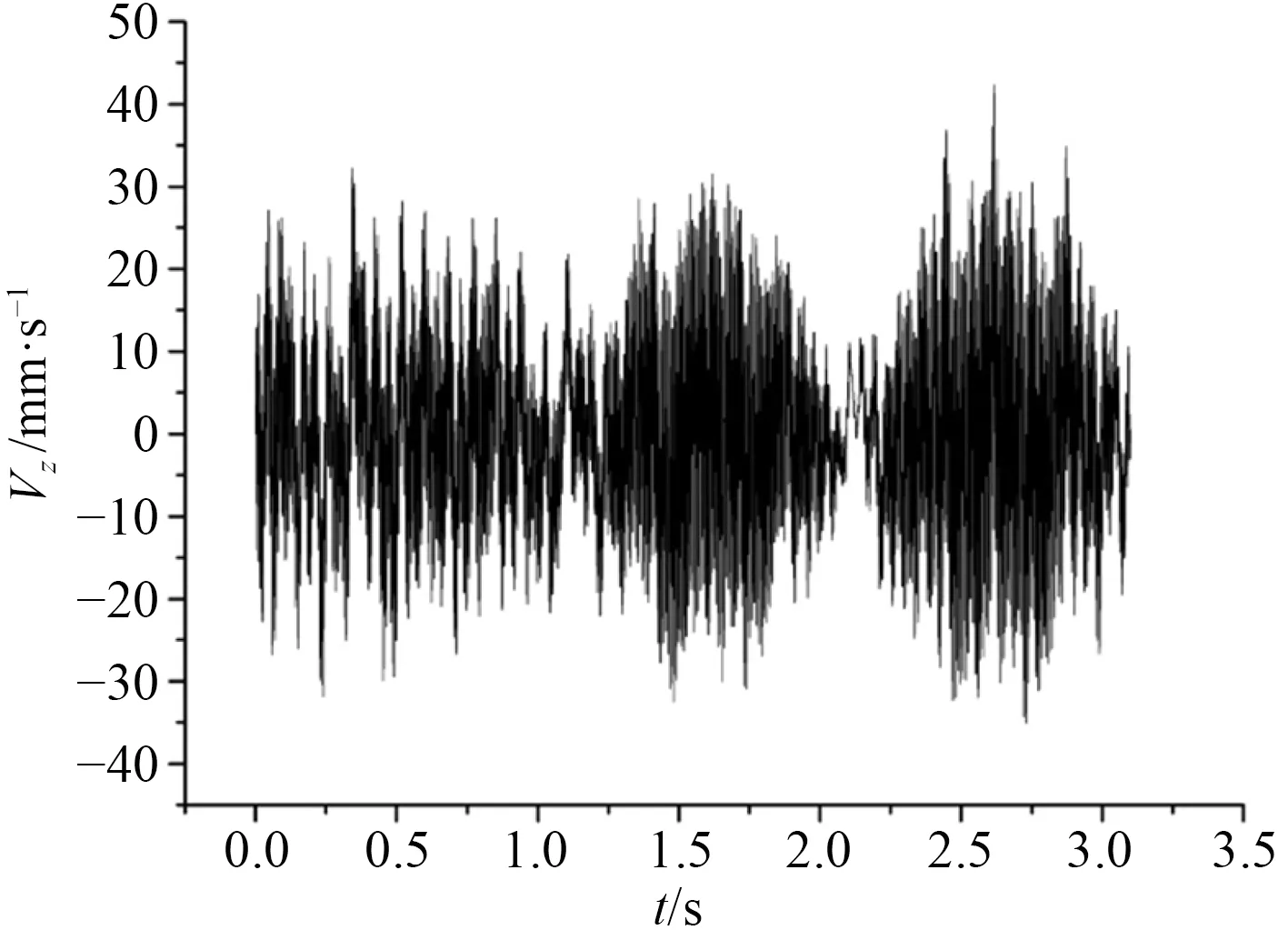
圖5 H1 點處垂向速度響應曲線Fig.5 Vertical velocity response curve at H1 point

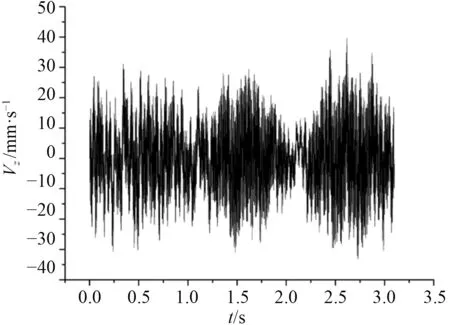
圖6 H2 點處垂向速度響應曲線Fig.6 Vertical velocity response curve at H2 point

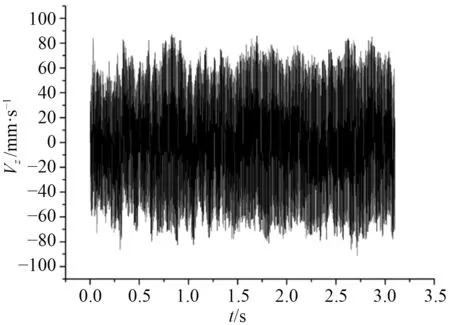
圖7 H5 點處垂向速度響應曲線Fig.7 Vertical velocity response curve at H5 point

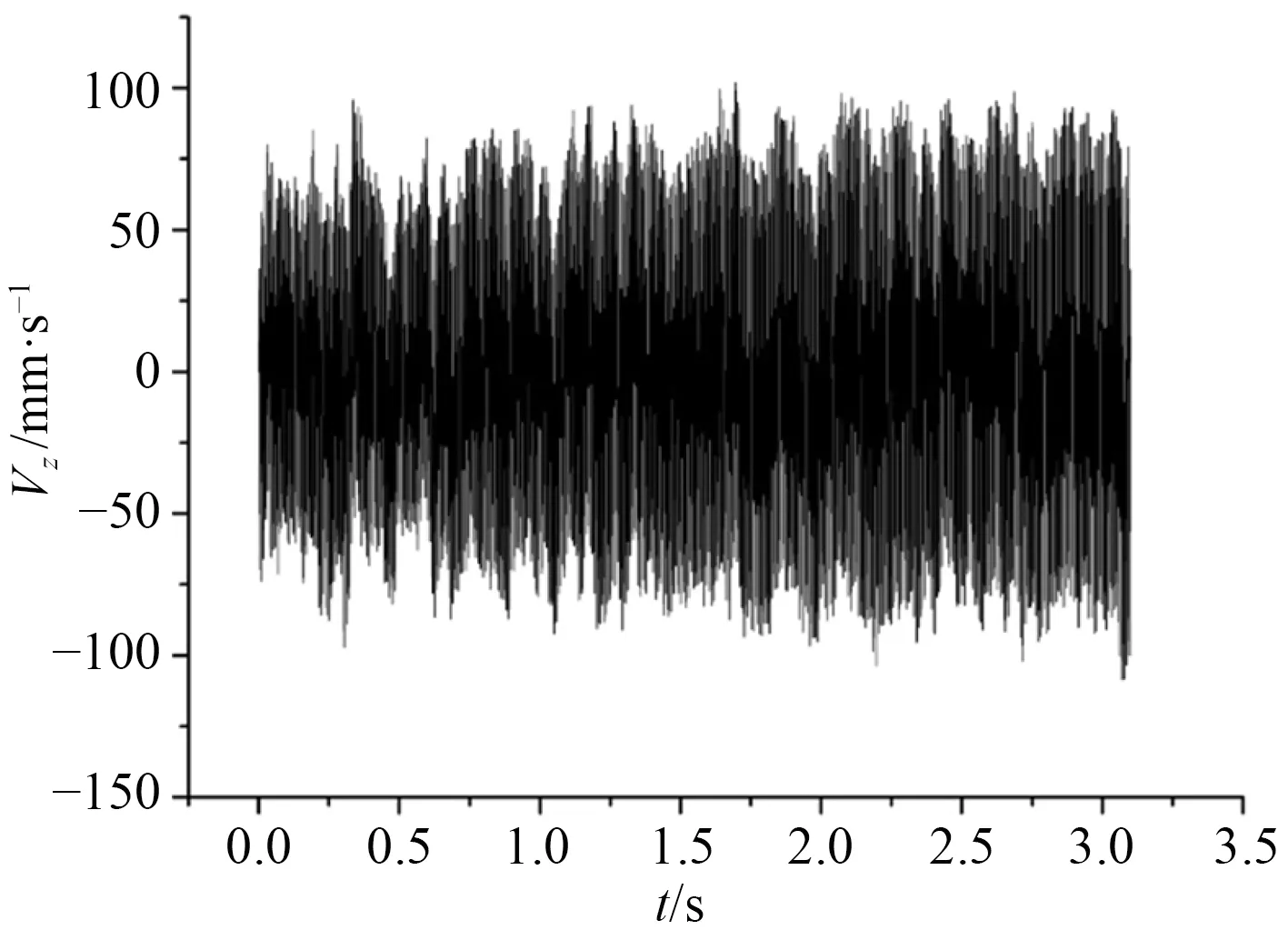
圖8 H6 點處垂向速度響應曲線Fig.8 Vertical velocity response curve at H6 point

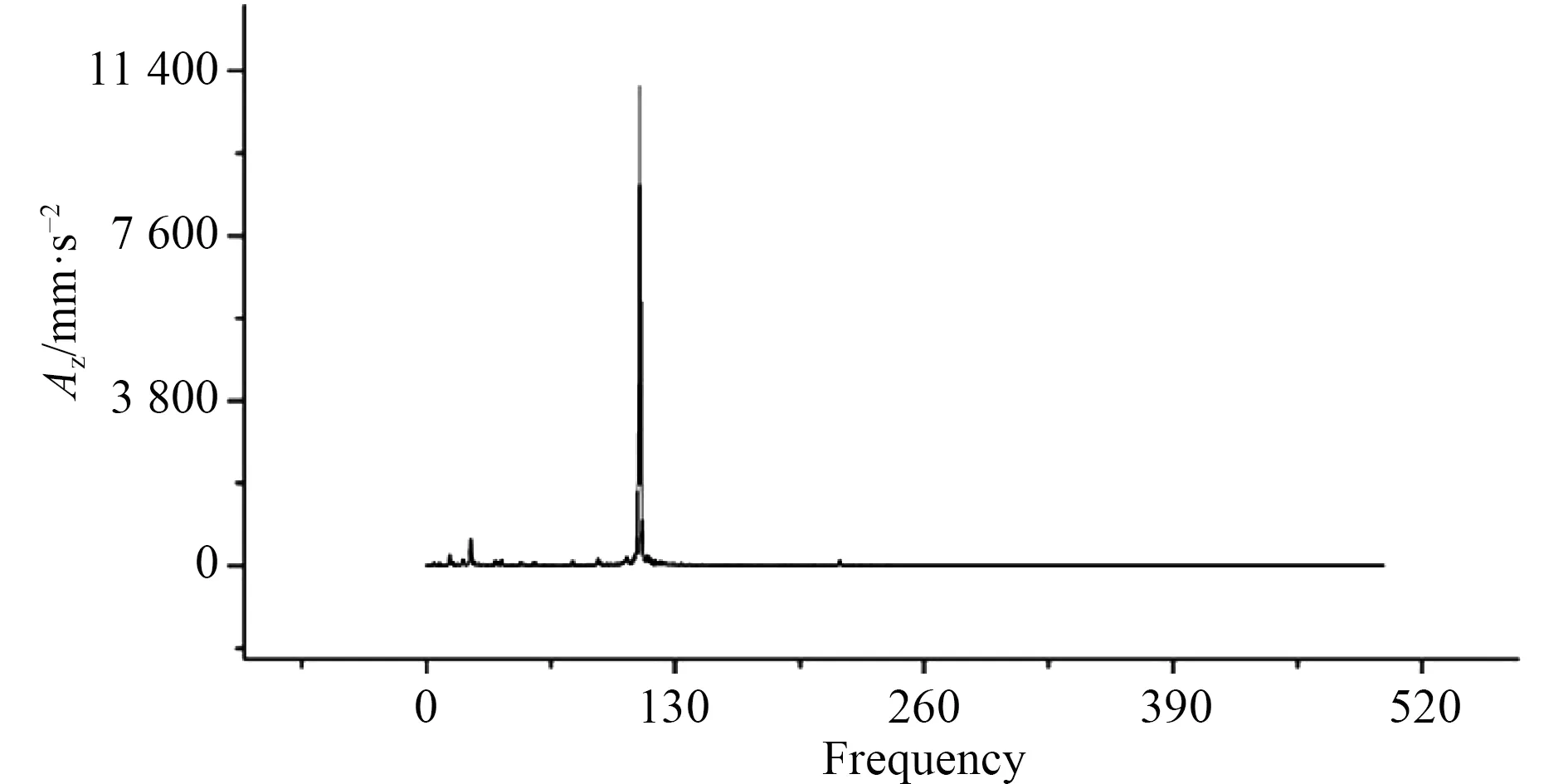
圖9 H2 點垂向加速度頻率響應曲線Fig.9 Frequency response curve of vertical acceleration of H2 point

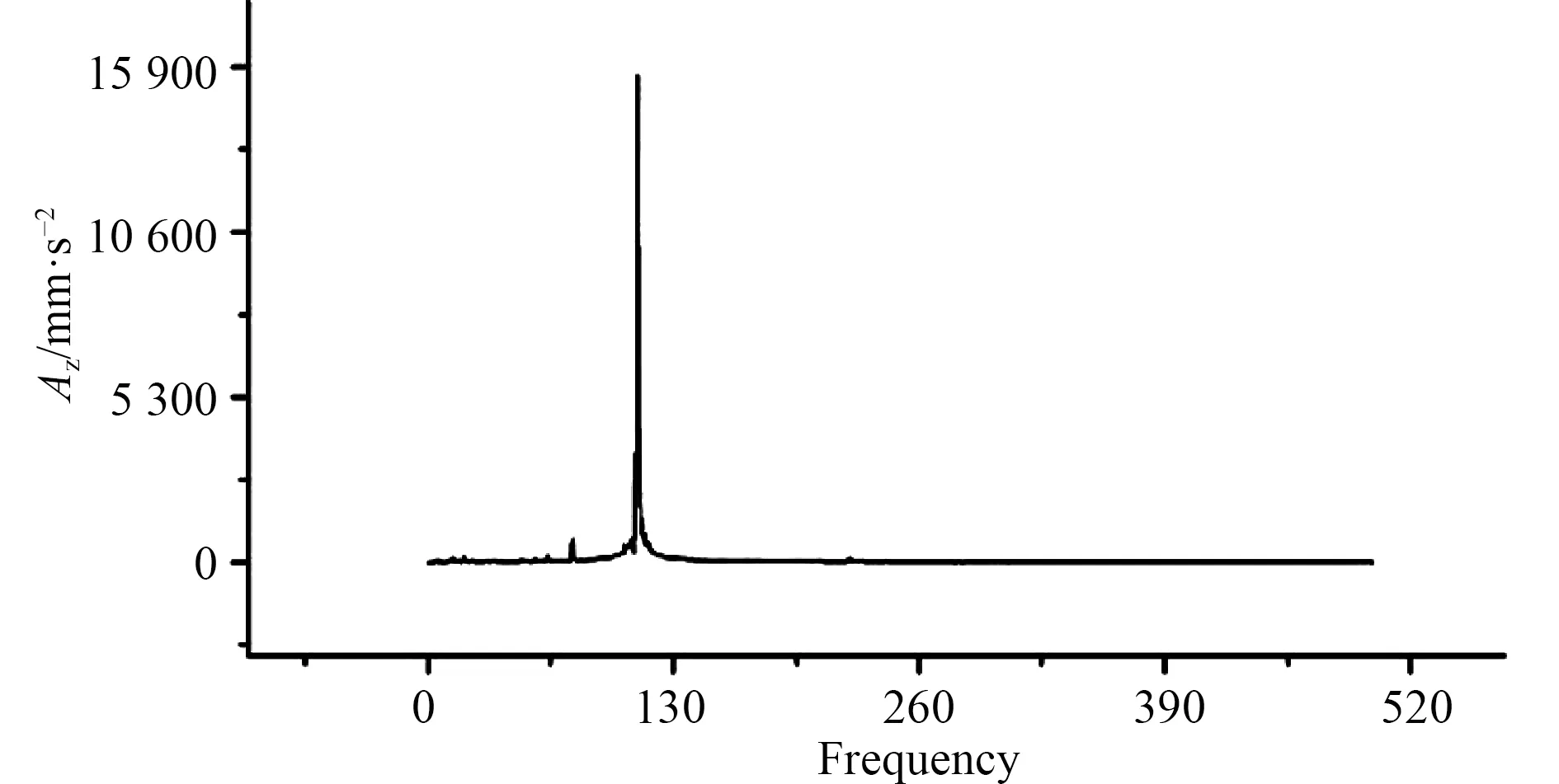
圖10 H6 處垂向加速度頻率響應曲線Fig.10 Frequency response curve of vertical acceleration of H6 point

3.2 計算分析及試驗對比

計算各測點在所有主要激振力共同作用下的瞬態響應值，參照GB/T 16 301-2008 標準，對測點在激振力下的響應計算數據按照如下公式處理，得到振動速度的均方根值。

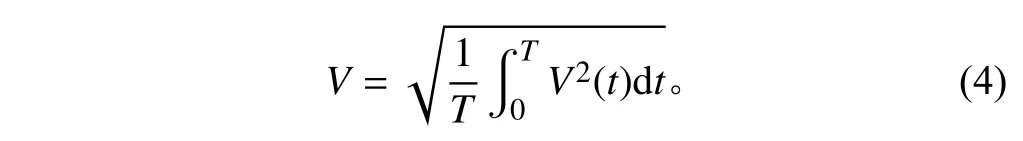
其中：V為振動速度的均方根值，mm·s?1，V(t)為振動速度隨時間變化的函數，mm·s?1；T為測量周期，s。

根據式（4）對所得時歷曲線進行處理，得到速度的均方根值，推進主機基座和墊升主機基座垂向速度頻率響應、橫向速度頻率響應以及垂向加速度的測試值和計算值如表3～表5 所示。

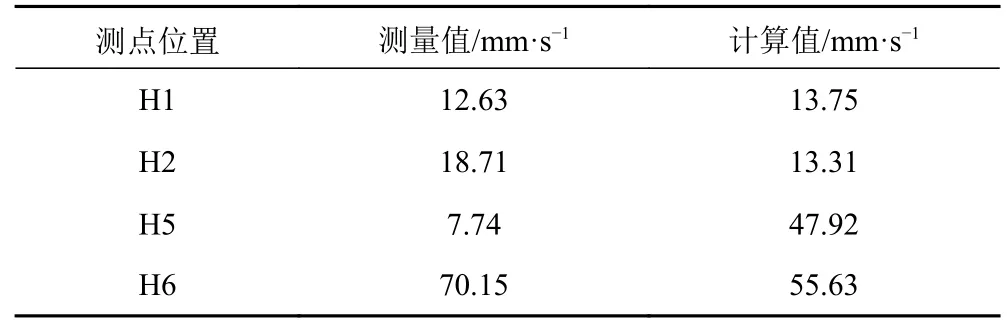
表3 垂向速度響應值對比Tab.3 Comparison of vertical velocity response values

表4 橫向速度響應值對比Tab.4 Comparison of lateral velocity response values

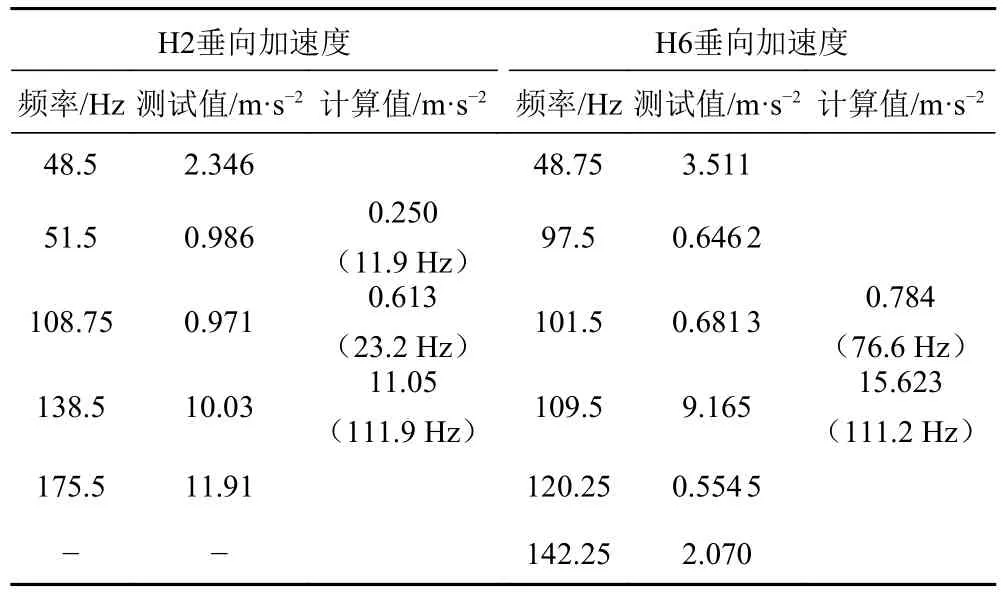
表5 垂向加速度響應值對比Tab.5 Comparison of vertical acceleration response values

計算值是參照GB/T 16 301-2008 標準，對測點在各個激振力共同作用下的瞬態響應計算數據按照均方根公式，得到速度的有效值。因此，計算值是考慮了不同激振源共同作用對測點響應的影響。由于在計算過程只考慮了幾個主要激振源，而實際上還有其他不可預估的激振源，再加上廠商提供的主要激振源計算數據有限，也會影響激振力計算的準確性，進而影響計算結果。

1）從垂向速度的測量值和計算值的結果來看，墊升主機基座位置（H1，H2）的測量值和計算值偏差不大。從空間位置來看，墊升主機基座距離推進主機和空氣螺旋槳較遠，這2 種激振源對墊升主機基座響應的影響較小，因此墊升主機基座響應主要來源于墊升主機激振源。墊升主機激振力估算準確，則計算結果就會與實測結果接近。推進主機基座位置（H5，H6）的測量值和計算值偏差較大。在估算推進主機和空氣螺旋槳激振力時，只考慮了由于機械不平衡引起的激振力，而空氣螺旋槳在工作時產生了不均勻的壓力場，由此引起的激振力估算困難，在計算時未予施加，也可能導致計算值與測試值偏差較大[10]。從測量結果來看，H5 與H6 的測量值也相差很大，若測試結果準確，則可能是H6 基座處的局部剛度過小。H5，H6 位置處的響應值從測試結果和計算結果來看均大于H1，H2處的響應值，是由于發動機短艙處的存在推進主機和空氣螺旋槳2 種激振源且短艙處的剛度要小于墊升機艙處的剛度。

2）從橫向速度的測量值和計算值的結果來看，H1 位置的測量值稍大于計算值，H5 位置的測量值與計算值較為接近，整體結果吻合較好。H1 位置和H5 位置的測量值均稍大于計算值，可能是計算時主要激振力估算稍小，也可能是其他激振力引起的基座處響應增加。

3）加速度計算值是由對測點在各個激振力共同作用下的瞬態響應計算得到。通過對時域內的響應進行傅里葉變換（FFT）得到加速度的頻率響應曲線。計算時激振源頻率只有12 Hz，111 Hz 和112 Hz 3 種。因此傅里葉變化后響應峰值應該在3 種頻率或其倍頻附近[11]。測試時，實船激振源有很多，H2，H6 測點在48.5 Hz 附近都存在一個峰值，此時應有一較大的激振力，推測為由于周圍流場不均勻引起的作用在空氣螺旋槳槳葉上的激振源頻率。H2 點處在138.5 Hz 與175.5 Hz 存在兩個大的峰值，推測可能為墊升主機實際頻率。H6 測點109.5 Hz 存在大的峰值，此值為推進主機的頻率。計算值在空氣螺旋槳的倍頻處存在較小的峰值，可能是空氣螺旋槳激振力估算偏小。計算值在主機激振力頻率存在最大峰值，理論上是合理的。

4 結 語

本文以有限元法入手，考慮對典型結構影響較大的振動源，將多個激振力同時施加在有限元模型上，得到測點的速度時歷，結合規范得到速度的均方根計算值，所得結論如下：

1）計算值與測試值吻合較好，同時施加多個主要振動源的激振力并基于此得到時歷速度，該方法可應用于船體振動分析；

2）在計算過程只考慮了幾個主要激振源，而實際上還有其他不可預見的激振源，再加上主要激振源計算數據有限，也會影響激振力計算的準確性，進而影響計算結果，因而確定振動源，并獲得準確的振動數據，對氣墊船振動評估尤為重要。