基于多種組合優化算法外形優化設計

謝 鵬，高志旺，王志東，凌宏杰

(1.江蘇科技大學 船舶與海洋工程學院，江蘇 鎮江 212003；2.江蘇科技大學 海洋裝備研究院，江蘇 鎮江 212003)

0 引 言

隨著能源成本的日益增加和環保技術的日趨嚴格，對船舶的節能技術提出了更高的要求。因此，可以通過船型優化、安裝船舶附體等方式提高船舶的快速性，來達到節能減排的效果。與此同時，船舶的快速性和耐波性是評價船舶性能的重要方式，在有波浪的惡劣海況下船舶會產生六自由度的搖蕩運動，其中，垂蕩、縱搖和橫搖運動會對船舶的操縱性、快速性產生重大的影響。為了提高船舶在復雜海況下的安全性，可以通過船型優化、安裝船舶附體等方式改善船體周圍流場，抑制船舶搖蕩，提高船舶在波浪中的運動和增阻性能。

提高船舶水動力性能的主要方式是改善其周圍流場，而安裝船舶附體是在不改變原有船型的基礎上改善其周圍流場最簡便可行的方式之一[1]。水翼和鰭[2]可增加船體附加質量與阻尼，可顯著減小船舶搖蕩程度，但與此同時它們也增加了船舶的濕表面積，通常會引起船舶阻力的增加，通常會在安裝水翼和鰭時在尾部安裝尾壓浪板、阻流板等其他附體減少船舶阻力的增加。尾壓浪板[3]是在船舶尾部向后延伸出的一塊板，通過增加船舶的虛長度，減少尾浪的方式改善尾部流場，從而減少船舶阻力。阻流板是船舶尾封板向下延伸出的一塊板，它能提供縱傾力矩和減少破波的產生。船舶附體在減阻減搖方面具有較大的應用前景，因此有必要對附體的水動力性能進行研究。隨著CAD 技術和CFD 技術的發展，使得船型和附體優化成為可能，通過分析船型參數和附體參數的改變對船體阻力性能的影響，進行特征參數的敏感度分析，可對船舶的改型設計提供幫助。在以后的改型設計中，設計者可以只通過調整敏感度大的參數，排除對船體阻力敏感度低的參數進行設計，節省設計人員工作時間，提高工作效率，縮短船舶建造周期。

本文以DDG1000 與球鼻首[4]組合新型DDG1000 船型為優化目標船型，建立與之對應的優化模型。為了提高尋優搜索的精度和速度，提出了組合優化策略[5–6]。在CAD 和CFD 集成優化框架內，運用組合優化策略對所建立起的船體模型進行求解，完成該船型線的優化，并對優化后的船舶阻力性能進行分析。

1 高速船型

1.1 初始船型

DDG1000 船長為182.88 m，型寬為24.6 m，設計吃水為8.4 m，航速為30 kn，按照縮尺比1∶70 進行船體建模。為使船體型線光順，本文將DDG1000 主要分為船體前部、船體中部、船體后部三大主要區域進行單獨建模。其中船體前部根據局部曲率復雜程度又細分為幾個小面。DDG1000 主要參數如表1 所示。

表1 船體模型主要參數Tab.1 Main parameters of hull model

而本文球鼻首由于特種裝備布置的需求，球鼻首參數較難選擇阻力最小的構型。該球鼻首附體要求模擬水滴形首部線型并滿足某型裝置布置的空間要求。

1.2 計算模型建立

基于三維建模軟件CAESES 完成DDG1000 的參數化建模，在不改變外形結構特征，忽略嚴重影響網格劃分的對水動力影響較小的部件前提下對模型進行簡化處理。

坐標原點位于DDG1000 尾封板位置處，指向首部為x軸正方向，左舷為y軸正方向，計算模型和網格劃分如圖1 和圖2 所示。

圖1 DDG1000 計算模型及坐標系Fig.1 DDG1000 calculation model and coordinate system

圖2 模型網格劃分Fig.2 Mesh generation of the model

1.3 數值計算和邊界設置

為準確進行DDG1000 的數值仿真，計算采用全六面體非結構網格，遵循整體非結構化，局部加密的原則。計算域為長方體域，因為船型是對稱型，故采用半船模型進行計算，長方體域5L*1.5L*2L（其中L為船長）。

模型數值計算的邊界條件設置如下：上下邊界選用規定壓力梯度，對稱面設置為mir 面，其他邊界采用速度遠場邊界，以均勻流場作為數值計算的初始條件；各個面選用壁面函數；整個流場采用非定常條件，在非定常計算過程中，取時間步長△t=0.01 s，流體參數設定為15℃海水，密度為1 026 kg/m3，動力粘性系數取0.000 9 Pa·s；

1.4 計算工況

計算航速包括低中高各個航速范圍，傅汝德數分別為0.2，0.25，0.3，0.35，0.4，0.45，0.5，0.55，對應的航速為1.01，1.26，1.52，1.77，2.02，2.28，2.53，2.78 八個工況。

1.5 結果對比

通過CFD軟件得到的仿真結果與實驗結果進行對比，如圖3 所示。可知，數值計算結果與試驗結果吻合良好，誤差小于2.5%，從而證明了本文所采用的數值方法的有效性.。

圖3 結果對比圖Fig.3 Comparison of results

2 基于多種組合優化算法優化方法

2.1 優化算法

遺傳算法[7–8]借鑒自然進化規律，模擬種群的進化過程，通過種群之間選擇、相互之間雜交和代數之間變異等獲取內部最優解，屬于具備生存和檢測的隨機搜索算法。NSGA-Ⅱ是最具影響力的多目標優化算法之一，有3 種突出特點：1）為了提高算法的收斂速度，采用快速非優勢排序；2）通過定義擁擠距離，有效避免了共享參數選擇的困難；3）采用精英策略，保證下一代種群優于上一代種群。因此，選擇NSGA-Ⅱ算法。

Sobol Method[9]是半隨機序列，基于低偏差序列的直升機易損性計算方法。該序列是一種穩定性和覆蓋性都非常好的隨機序列，與局部法相比的Sobol 方法具有參數變動范圍可擴展到整個參數定義域。

Tangent Search Method[10]為切線搜索法，屬于直接搜索方法，被用作搜尋任意超過一個設計變量且受任意等式和不等式非線性約束問題的最小值。切線搜索法的基本思想是：當一個試探移動通過約束邊界時，在當前可行的基點上不滿足約束函數的偏導數將會被近似替代。這是通過最基本的差分方法來執行的。利用差分法對目標函數的偏導數進行近似處理，在考慮進一步計算之前，這個差分法就可以用一個單獨的函數來進行描述。每一次試探搜索都是為了減少不必要的評估約束函數的輔助運算過程，以此來提高搜索效率。隨后，一個試探性移動將會在一個超平面上執行，這一超平面是和約束函數的超曲面相切的平面（這一超平面可以向可行域微小地移動，以便這個超平面能夠將當前的基礎解包含在內）。如果這個探索是成功的，那就稱這次試探為“切線試探”。因為切線搜索法完全不需要考慮目標函數的梯度，所以計算效率得到了很大的提高。

2.2 優化方案

對船體型線進行優化，首先要選擇合適的優化算法，適當的優化算法可以提升優化精度與速度。首先選擇Sobol 算法，然后Sobol 優化算法與NSGA-Ⅱ優化算法進行組合，Sobol 優化算法與Tangent Search Method 優化算法進行組合，比較這2 種優化算法的優點。優化目標為在設計航速2.02 m/s 的情況下阻力最優。

在優化之前需要建立恰當的優化模型，對DDG1000進行優化獲得最小阻力是典型的最優化問題。最優化問題都有關鍵因素包括優化目標、設計變量、約束條件。

1）設計變量的選擇

對船體進行優化時，選擇的重點優化對象為球鼻首，球鼻首的高度變形曲線、寬度變形曲線，長度變形曲線、球鼻首最低處特征曲線的正切值，最高處特征曲線的正切值，球鼻首與船體過渡曲面的高度值，船體尾部特征曲線正切值等11 個值作為設計變量。

2）約束條件的選擇

為了使得優化后的船體模型滿足設計要求和進行優化前后的對比，需要對船體模型進行一些有必要的約束，選擇在優化過程中，船體的排水量保持不變。

3）優化目標的選擇

選擇在設計航速2.02 m/s 的條件下船體總阻力最小。

3 優化結果分析

3.1 組合優化算法結果分析

利用Sobol 優化算法、NSGA-Ⅱ優化算法作為第1 組優化組合算法，Sobol 優化算法、Tangent Tsearch Method 優化算法作為第2 組優化組合算法，在生成船體模型個數相同的基礎上，計算消耗時間相差不多，第1 組稍微短一些；生成的船體模型阻力第1 組最優，其中第2 組優化算法阻力值結果比較集中趨于某一個值，有可能陷入局部最優解中。綜上比較，第1 組組合優化算法比第2 組組合優化算法具有優勢。

3.2 設計變量變化分析

如上所述，第1 組優化組合算法具有較大優勢，因此所選取的設計變量分析結果，都取自第1 組組合優化算法。

表2 為船體模型設計變量優化前后的對比。可以看出，設計變量的變化都在取值范圍內，符合要求。從球鼻首的長度、高度、寬度變形結果來看，球鼻首的長、寬雖有增加，但對船體阻力不敏感，球鼻首的高度變形對船體阻力比較敏感，最終球鼻首變成抬首型。

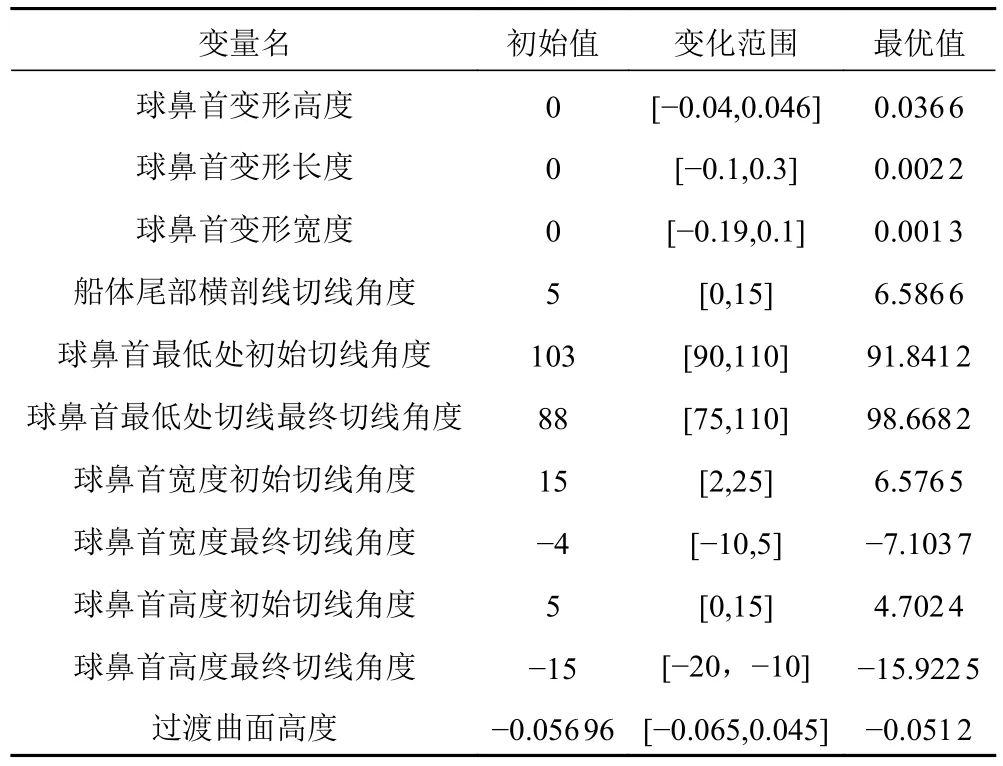
表2 設計變量Tab.2 Design variable

3.3 阻力結果對比分析

以設計航速2.02 m/s 速度下的總阻力為優化目標，并對各種阻力成分進行分析，并加算對比速度為1.77 m/s 下的阻力變化，如果如表3 所示。

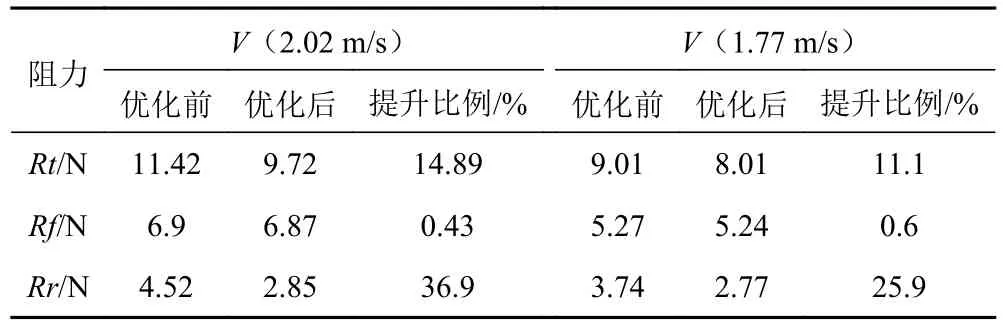
表3 阻力變化Tab.3 Resistance change

在2.02 m/s 的速度下，優化后的總阻力為9.72，比優化前的總阻力減少14.89%，摩擦阻力減少0.43%，剩余阻力減少36.9%。在1.77 m/s 的速度下，優化后的總阻力為8.01，比優化前的總阻力減少11.1%，摩擦阻力減少0.6%，剩余阻力減少25.9%。在優化過程中，船體的排水量保持不變，船體的濕表面積基本不變，所以摩擦阻力基本不變，通過優化球鼻首，改善了船體周圍的壓力分布，減少了興波阻力。圖4 和圖5 分別表示優化前后的船體模型。

圖4 優化前船體模型Fig.4 Pre-optimization hull model

圖5 優化后船體模型Fig.5 Optimized hull model

圖6 和圖7 分別為優化前后的自由液面波形圖。可以看出，優化后船首周圍波形數減少變稀疏，有助于減少船首周圍的興波阻力。

圖6 優化前自由液面波形圖Fig.6 Free surface waveform before optimization

圖7 優化后自由液面波形圖Fig.7 Waveforms of optimized free surface

4 結 語

本文利用CFD 軟件對新型DDG1000 的水動力性能開展了數值計算分析，并將CFD 結果與試驗結果進行對比，驗證數值方法的準確性。利用CAESES軟件對DDG1000 進行參數化建模，基于FINEMARINE 和CAESES軟件集成平臺，基于在設計航速為2.02 m/s，采用2 種組合優化算法對船型進行優化，并對比了2 種組合優化算法的優缺點。結果證明，優化后的總阻力減少14.89%，摩擦阻力減少0.43%，剩余阻力減少36.9%。