Welander自然循環問題高精度數值模擬

巢 飛，楊 文，邰 云，邱金榮，單建強

(1.武漢第二船舶設計研究所，湖北 武漢 430064；2.西安交通大學 核科學與技術學院，陜西 西安 710049)

0 引 言

自然循環是指依靠密度差和高度差形成的驅動力驅動流體循環流動的現象。自然循環在核動力系統中非常常見，其對反應堆安全有重要影響，因此準確模擬自然循環現象是當前反應堆熱工水力分析中最重要研究內容之一。

目前主流熱工水力系統分析程序如RELAP5，CATHARE，TRACE 等普遍采用低階差分法來求解基本守恒方程，其在模擬自然循環不穩定性問題時存在預測誤差。為提高自然循環不穩定性問題的計算精度，本文采用基于兩流體雙壓力兩相流模型的高精度數值解法對Welander 自然循環進行計算分析。

1 兩流體雙壓力模型

兩流體雙壓力模型基本守恒方程：

體積份額輸運方程

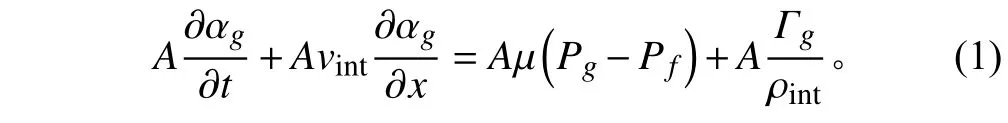
式中：αg表示汽相體積份額；Pg和Pf分別代表汽相和液相壓力，Pa；vint為相間界面速度，m·s?1；μ為壓力松弛因子，Pa?1·s?1，表示汽液兩相壓力達到平衡的松弛速率；A為管道截面積，m2；ρint為相間界面密度，k g·m?3；Γg為單位體積液-汽相間質量交換率，kg·m?3·s?1。汽、液兩相體積份額關系應滿足：

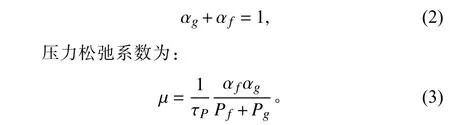
其中 τP為壓力松弛時間，s。

質量守恒方程

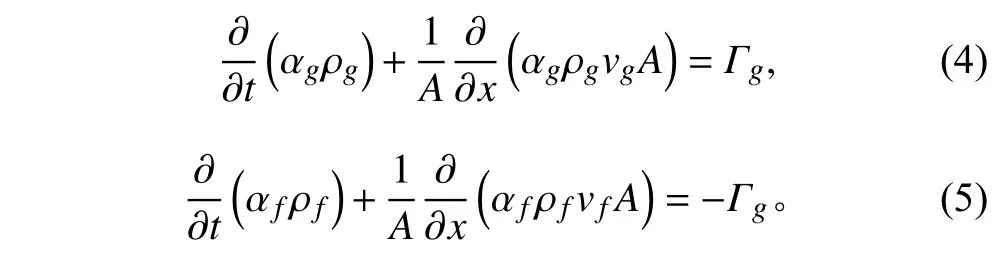
式中：Γf=?Γg為單位體積汽-液相間質量交換率，kg·m?3·s?1；ρ為相密度，kg·m?3；v為相速度，m·s?1；f為液相標識；g為汽相標識。

動量守恒方程：

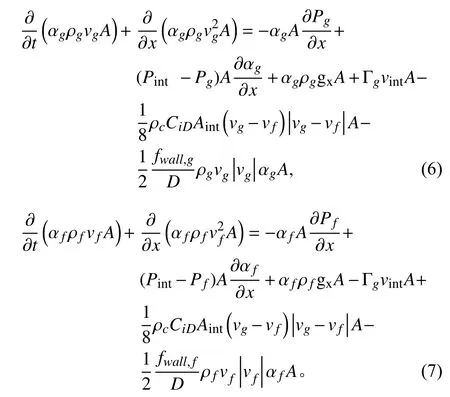
式中：Pint為相間界面壓力，Pa；fwall,k為阻力系數;ρc為連續相密度，kg·m?3；CiD為相間阻力系數；Aint為單位體積相間界面面積，m?1；gx為重力加速度在流動方向的投影，m·s?2。

能量守恒方程

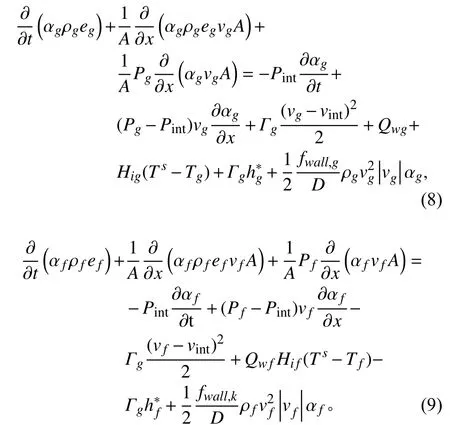
式中：ek為k相比內能/J·kg?1；Qwg為汽相單位體積壁面換熱量，W·m?3；Qwf為液相單位體積壁面換熱量，W·m?3；Hig為單位體積相間界面到汽相的換熱系數，W·m?3·K?1；Hif為單位體積相間界面到液相換熱系數，W·m?3·K?1；Ts為相間界面溫度，Tk為k相溫度，K；為相間界面汽相比焓，J·kg?1；為相間界面液相比焓，J·kg?1。

2 高精度數值算法

2.1 半隱式數值解法

采用參考文獻[1]作者提出的半隱數值算法求解兩流體雙壓力模型。為達到快速計算的效果，半隱算法只對時間常數小、傳播速度快的量隱式處理，如兩相速度、壓力梯度、相間界面質量和動量交換項，其他量顯式處理。為了解決兩相和單相之間轉變帶來的數值不穩定性問題，動量守恒方程和質量守恒方程處理成和與差的微分方程，所有守恒方程瞬態項采用展開的形式，再進行數值差分。采用交錯網格劃分控制體，如圖1 所示。K，L等表示求解質量、能量守恒方程的控制體，存儲流場中的標量如壓力、比內能、空泡份額等；j代表動量控制體（虛線包圍），用于求解動量守恒方程，存儲流場中速度矢量。

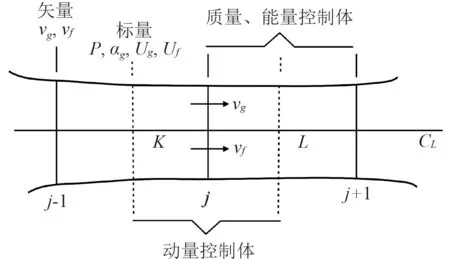
圖1 交錯網格示意圖Fig.1 Schematic drawing of staggered mesh

2.2 瞬態項二階差分格式

目前現有的系統程序普遍采用一階時間差分（BDF1）離散守恒方程瞬態項。BDF1 離散誤差大，給守恒方程的差分方程引入了“人工”擴散，宜采用精度更高的二階時間差分（BDF2）來降低瞬態項的離散誤差。二階時間差分根據Taylor 級數展開法得到[2]：

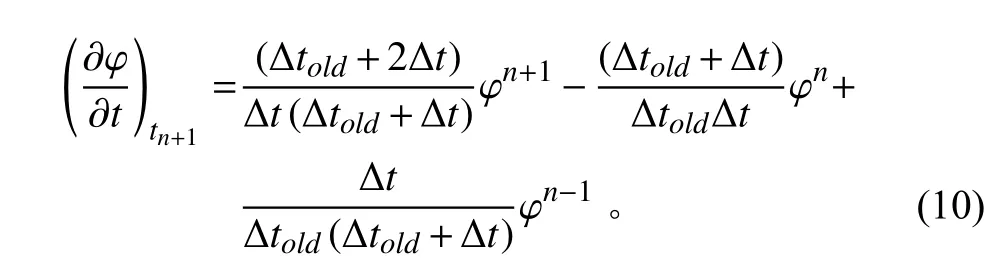
其中：?φ/?t表示守恒方程中的瞬態項，Δt=tn+1?tn，Δtold=tn?tn?1。該式考慮了時間步長的變化，具有一般性，在系統程序中應用更為方便。BDF1 和BDF2 可處理成統一形式：

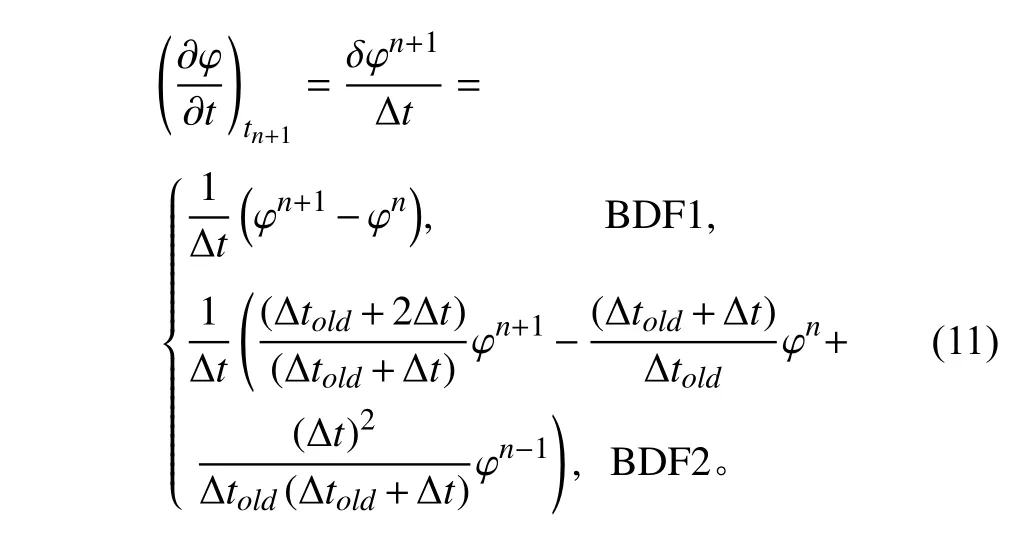
2.3 對流項三階TVD 差分格式

目前主流熱工水力程序采用一階施主元法離散對流項。一階施主元法本質上是一階迎風，計算精度低，因此宜采用穩定高階施主元法，以提高對流項的計算精度。雙壓力模型守恒方程中與速度相關的項均采用施主元法計算。以能量方程對流項為例，其離散形式為：

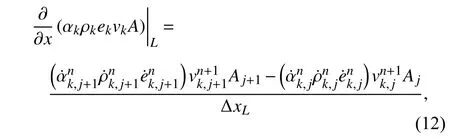
由于速度本身定義在接管上，因此對流項的計算精度很大程度上取決于接管上的標量（如）的計算方案。接管上標量數值計算的統一形式可以寫成：

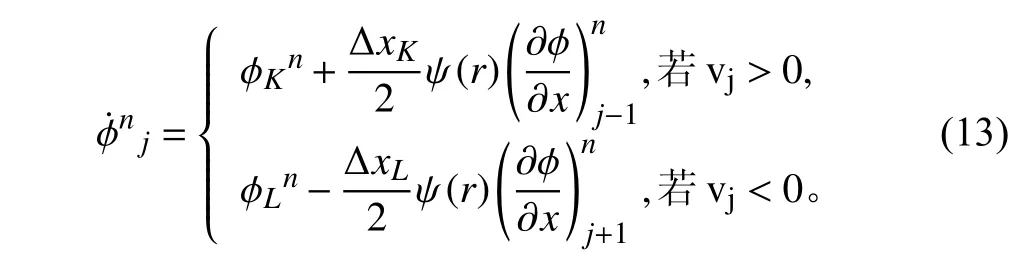
其中：Δx是控制體長度；?φ/?x是控制體邊界上的梯度；ψ(r)為通量限制函數；r為梯度比，由下式給出：

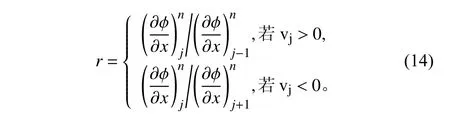
空間離散方案統一形式（13）由兩部分組成，第一部分為穩定的一階迎風方案，第二部分為反擴散項。因此，物理量 φ˙計算精度由反擴散項中的通量限制函數ψ(r)決定。

穩定三階TVD 差分格式（命名為TOU_TVD_CFL）為[2]：

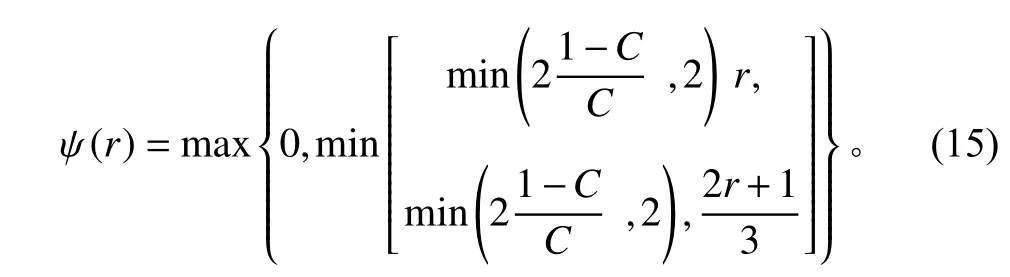
式 中C為Courant 數。

3 計算分析

3.1 Welander 自然循環問題

Welander 提出了豎直回路中單相自然循環問題來研究流體的不穩定性行為[3]。Welander 自然循環回路由2 個平行的豎直絕熱管，頂部冷源和底部熱源組成，如圖2 所示，回路總長為L，截面積為A，熱阱和熱源長度為 Δs。通過頂部熱阱的冷卻和底部熱源加熱，流體在回路頂部和底部產生密度差，從而驅動流體發生自然循環流動。通過選擇合適的浮力與摩擦阻力的比值，流動可能會出現穩定、弱不穩定和強不穩定行為。在文獻[3]中，Welander 推導了實驗回路層流下流動不穩定性理論邊界，Ambrosini 和Ferreri[4]將不穩定性邊界擴展湍流情況，如圖3 所示。Welander 自然循環穩定性邊界繪制成無量綱重力系數 α和無量綱摩擦系數 ε的關系式圖，無量綱量具體表達式為：

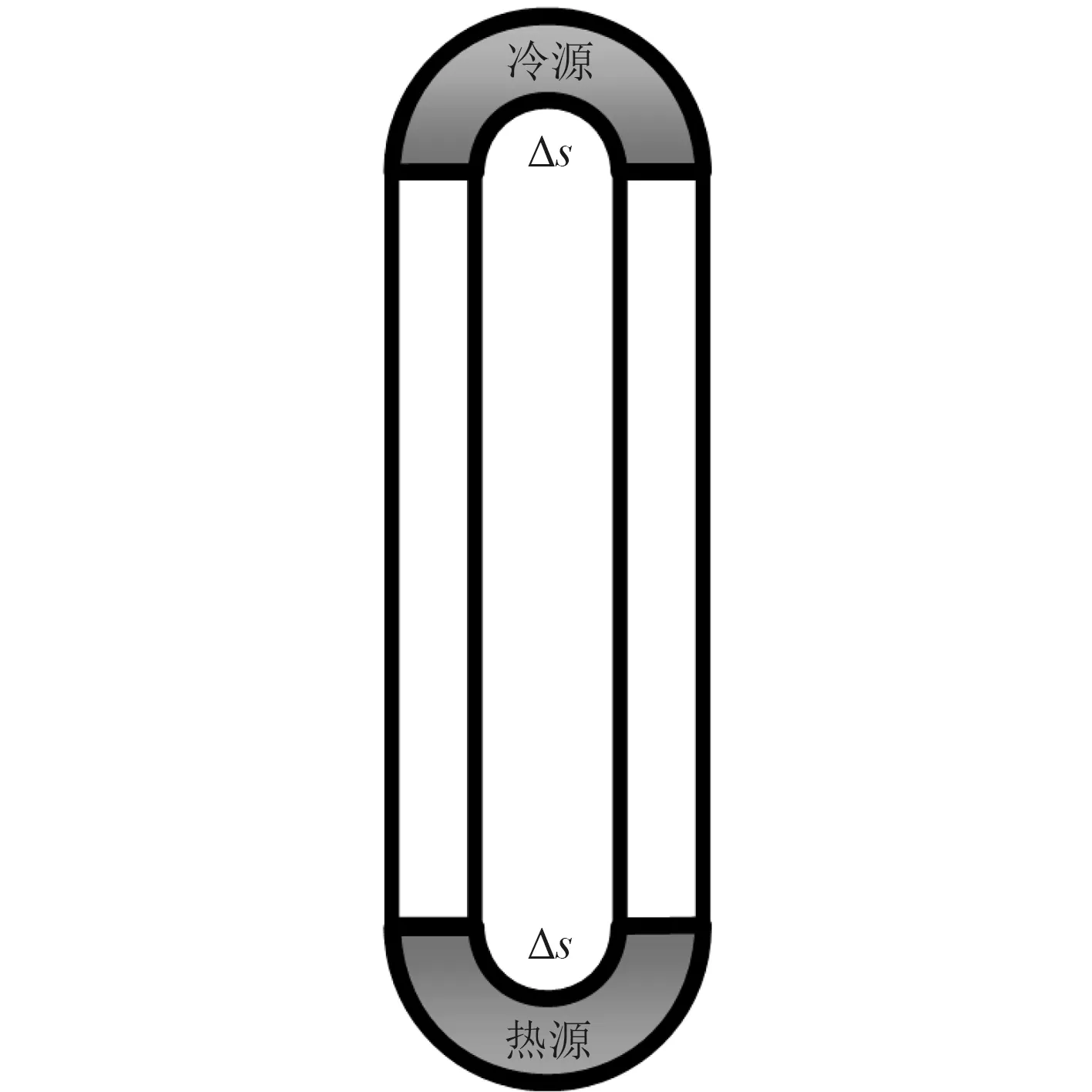
圖2 Welander 自然循環問題示意圖Fig.2 Schematic diagram of Welander natural circulation

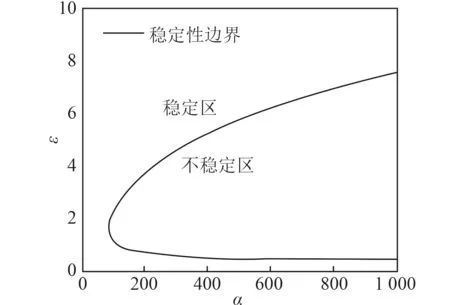
圖3 Welander 自然循環問題流動不穩定性邊界Fig.3 Flow instability map of Welander natural circulation

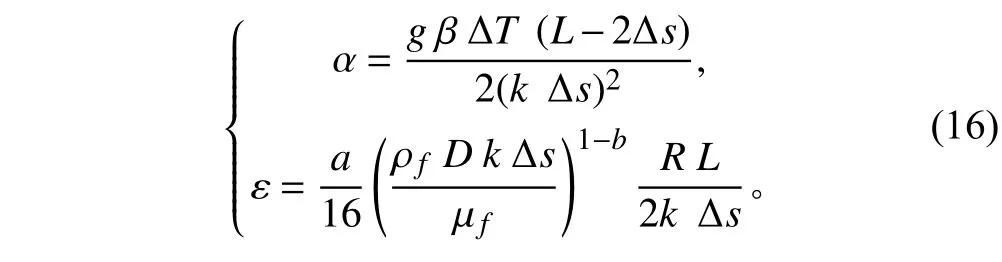
式中：Welander 定義的層流摩擦系數為R=64/Ref·Welander 定義的換熱系數為溫差ΔT=當a=0.316 4/4,b=0.25時，表示湍流條件；當a=16,b=1時，表示層流條件。

對于Welander 單相振蕩自然循環問題，選取Ambrosinia 和Ferreri[5]設置的幾何參數和邊界條件。管內徑為0.1 m，熱源和冷源長度為0.1 m。管道充滿壓力為0.1 MPa 的過冷水。熱源溫度為30℃，與流體換熱系數為20 000 W·m?2·K?1，冷源溫度維持20℃，與流體換熱系數為20 000 W·m?2·K?1。本文研究Welander 單相振蕩自然循環問題3 個不同的實驗工況：強不穩定模式、弱不穩定模式和穩定模式，見表1。圖4 給出了Welander 自然循環回路數值模擬節點圖。在進行模擬計算時，時間步長為0.5 s，熱源和冷源分別采用一個節點模擬，兩垂直絕熱管都均分為N個控制體，因此環路控制體總數為2N+2。

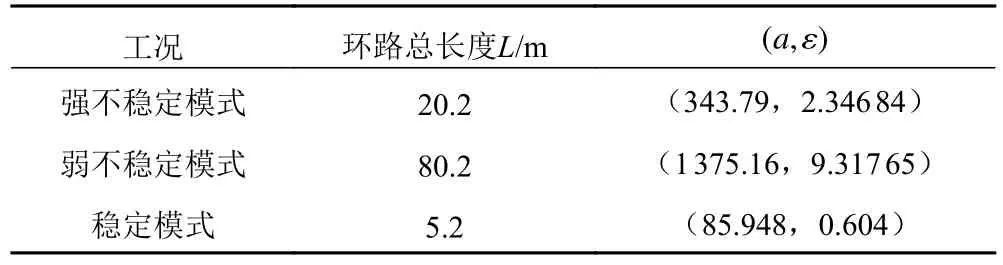
表1 Welander 自然循環問題實驗工況Tab.1 Test conditions of Welander natural circulation

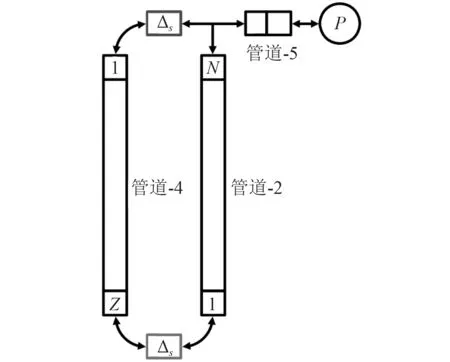
圖4 Welander 自然循環節點圖Fig.4 Nodalization of Welander natural circulation

3.2 數值結果

對于強不穩定模式工況，環路長度取L=20.2 m，此時 (α,ε)為 (343.79,2.346 84)。強不穩定模式時，實驗回路流量出現流動反轉現象，并作平均速度為零的等幅振蕩。為便于觀測到流動不穩定性行為，實驗之初，給定回路一個極小流量的擾動。

圖5 給出了使用低階差分方案BDF1+FOU 在不同控制體數下的數值結果。由圖可知控制體數低于62 時，數值誤差過大，無法預測出不穩定行為；控制體數達到102 時才預測出不穩定性行為，控制體數越多，數值誤差越小，預測的不穩定行為振蕩周期越短。由于數值誤差的阻尼作用，粗糙網格可以穩定物理上不穩定的系統。采用不同計算節點，低階差分數值結果會出現系統穩定和不穩定2 種相矛盾的情況。因此數值誤差對不穩定性行為準確預測有很不利的影響，低階差分方案BDF1+FOU 精度低，不利于研究流動不穩定行為。

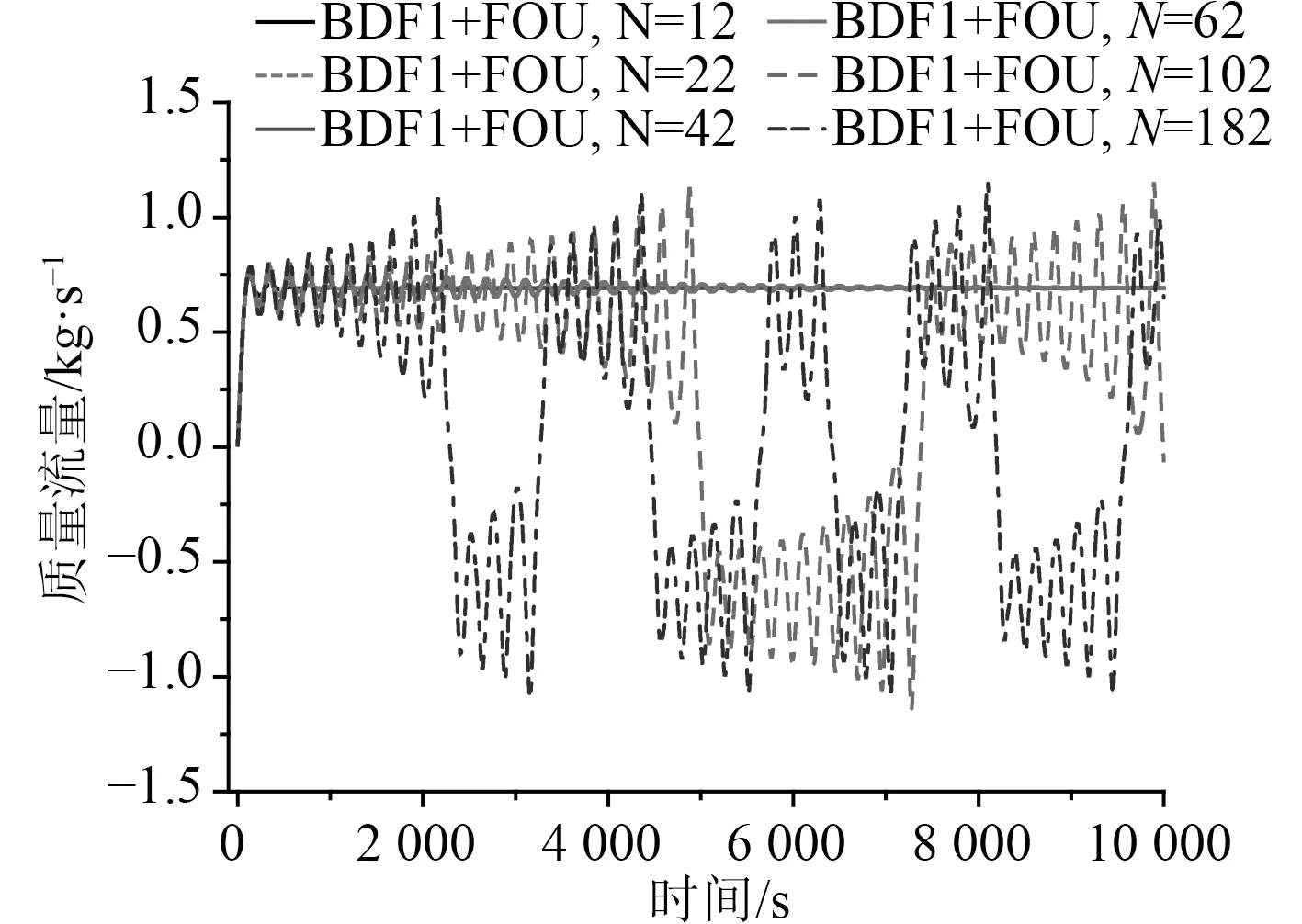
圖5 強不穩定模式質量流量：低階BDF1+FOU方案的計算結果Fig.5 Mass flow of strong instability mode:calculation results of BDF1+FOU scheme

圖6 給出了高階差分方案與低階差分方案結果的對比。高階差分方案模擬流動不穩定性行為具有相當大的優勢。高階差分方案TOU_TVD_CFL 只需22 個控制體就可以預測出不穩定行為，因此高階算法有效減小了數值擴散，提高了計算精度。高階差分算法采用22 個控制體的數值精度可達到低階差分算法控制體數為182 的計算精度，振蕩周期相近。

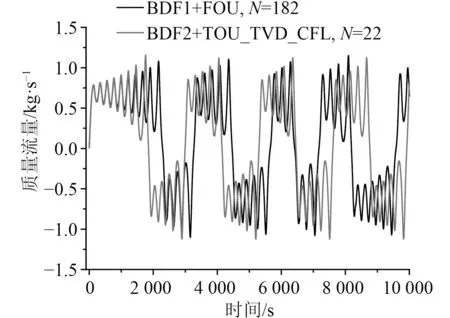
圖6 強不穩定模式質量流量：高階和低階方案的計算結果對比Fig.6 Mass flow of strong instability mode:comparison between low order and high order difference scheme

圖7 給出了低階差分方案BDF1+FOU 計算的流體溫度與質量流量關系圖，隨著控制體數增多，精度越高，混沌行為（Chaotic Behavior）越明顯。圖8 給出了高階BDF2+TOU_TVD_CFL 方案計算的流體溫度與質量流量關系圖。同樣可以看出，隨著控制體數增多，可以預測到流動反轉的混沌演化過程，流體溫度與質量流量關系圖類似蝴蝶形狀。

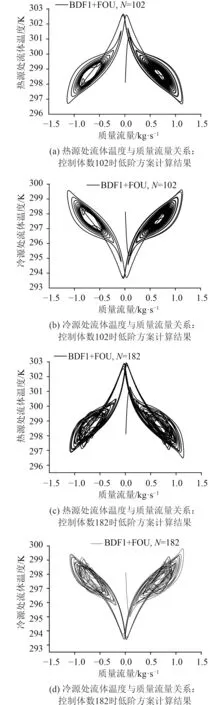
圖7 低階方案BDF1+FOU 計算的流體溫度與質量流量關系圖Fig.7 Fluid temperature versus mass flow calculated by low order scheme BDF1+FOU

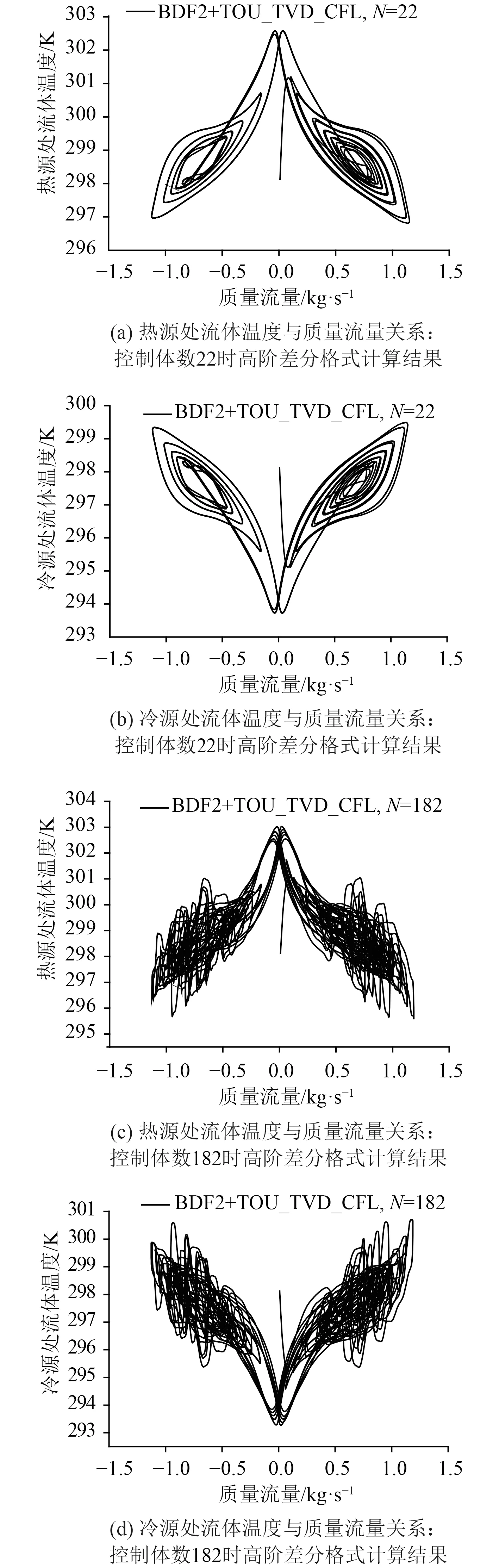
圖8 高階BDF2+TOU_TVD_CFL 方案計算的流體溫度與質量流量關系圖Fig.8 Fluid temperature versus mass flow calculated by high order scheme BDF2+TOU_TVD_CFL

針對弱不穩定工況，回路總長為80.2 m。弱不穩定模式時，回路流量不會出現流動反轉現象，其維持一個流動方向上的近似等幅振蕩。圖9 給出了采用低階方案計算的質量流量隨時間變化圖。控制體數為722 時質量流量的數值結果依舊出現緩慢的衰減，低階差分結果誤差大。圖10 給出了弱不穩定工況下采用高階差分方案計算的質量流量隨時間變化圖。高階算法的結果有效減小人工粘性，抑制振蕩衰減，控制體數為102 時就可以模擬出等幅振蕩的流動不穩定性行為。

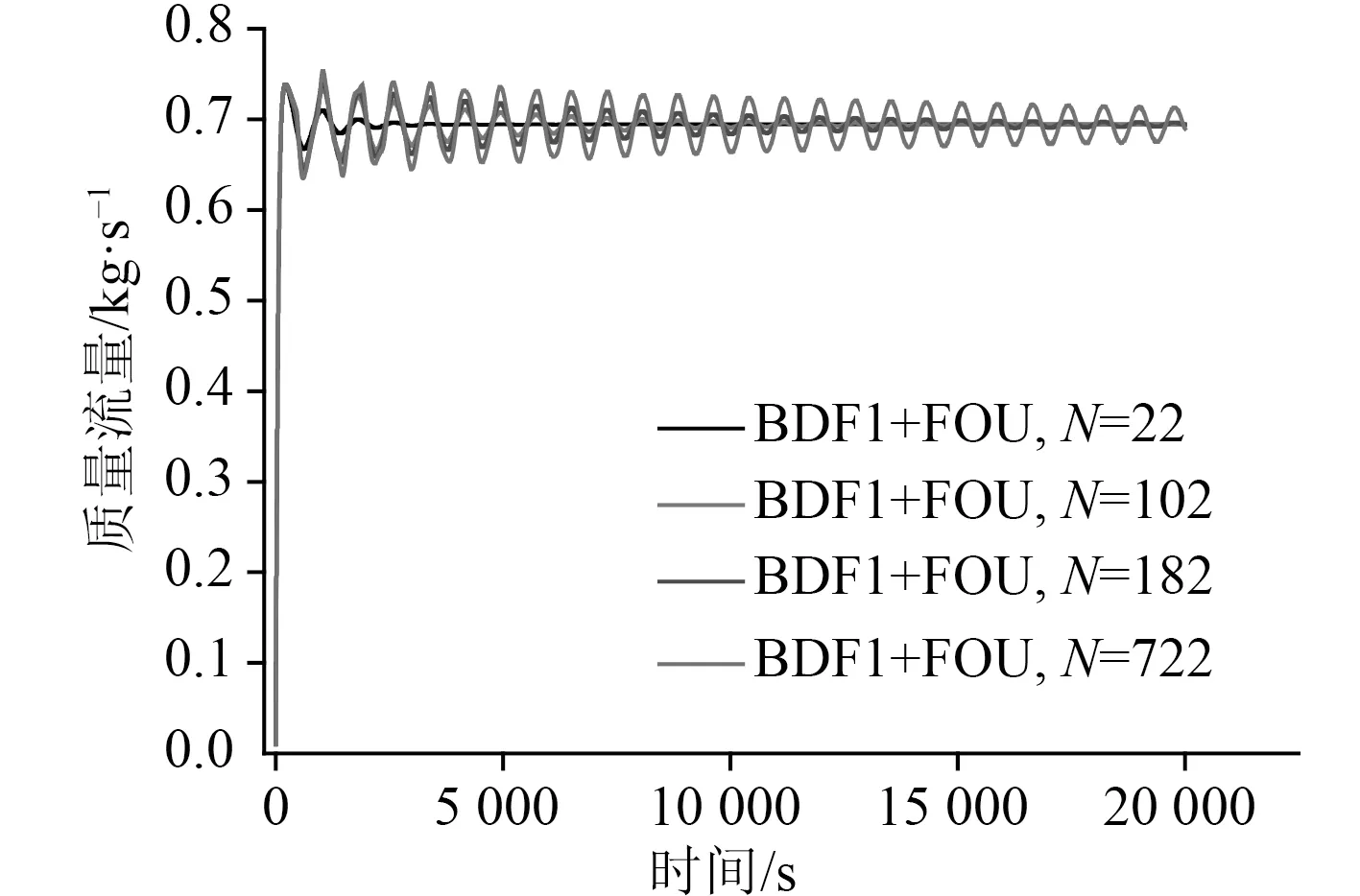
圖9 弱不穩定模式質量流量低階方案的計算結果Fig.9 Calculation results of low order scheme by mass flow of weak instability mode

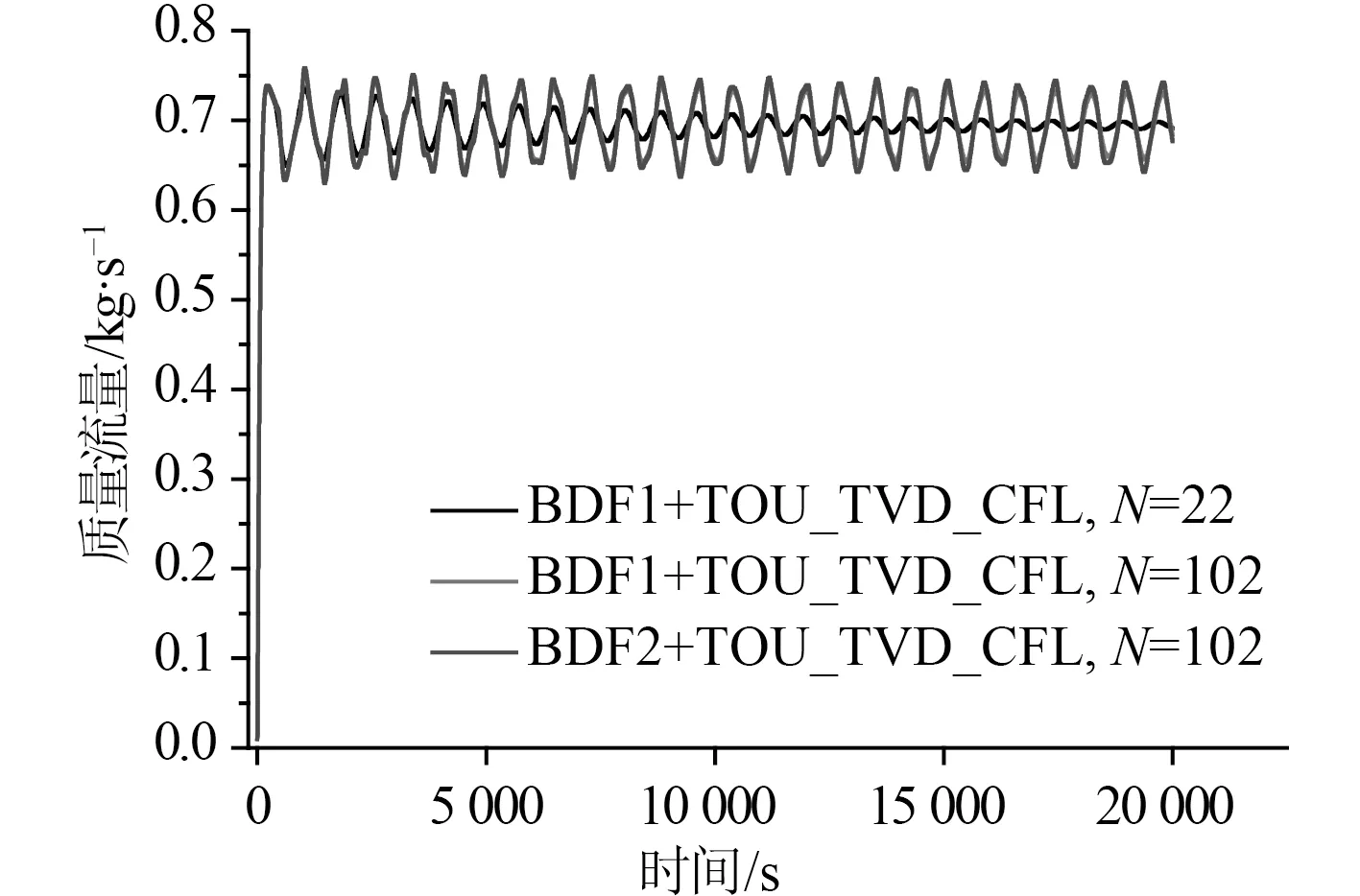
圖10 弱不穩定模式質量流量高階方案的計算結果Fig.10 Calculation results of high order scheme by mass flow of weak instability mode

針對L=5.2 m 的穩定模式工況，表現為：質量流量初始增加到最大值，然后經過一段時間的衰減型振蕩后維持穩定運動。圖11 和圖12 給出了穩定模式工況下質量流量的計算結果，高階方案與低階方案計算結果對比見圖13。因為人工粘性的影響，低階差分預測更小的振蕩振幅，更快達到穩定狀態；控制體數為102 的低階結果精度比控制體數為22 的高階結果精度還低，振蕩衰減更快。由于高階差分對穩態沒影響，最終高階差分預測的穩態流量與低階結果一致。

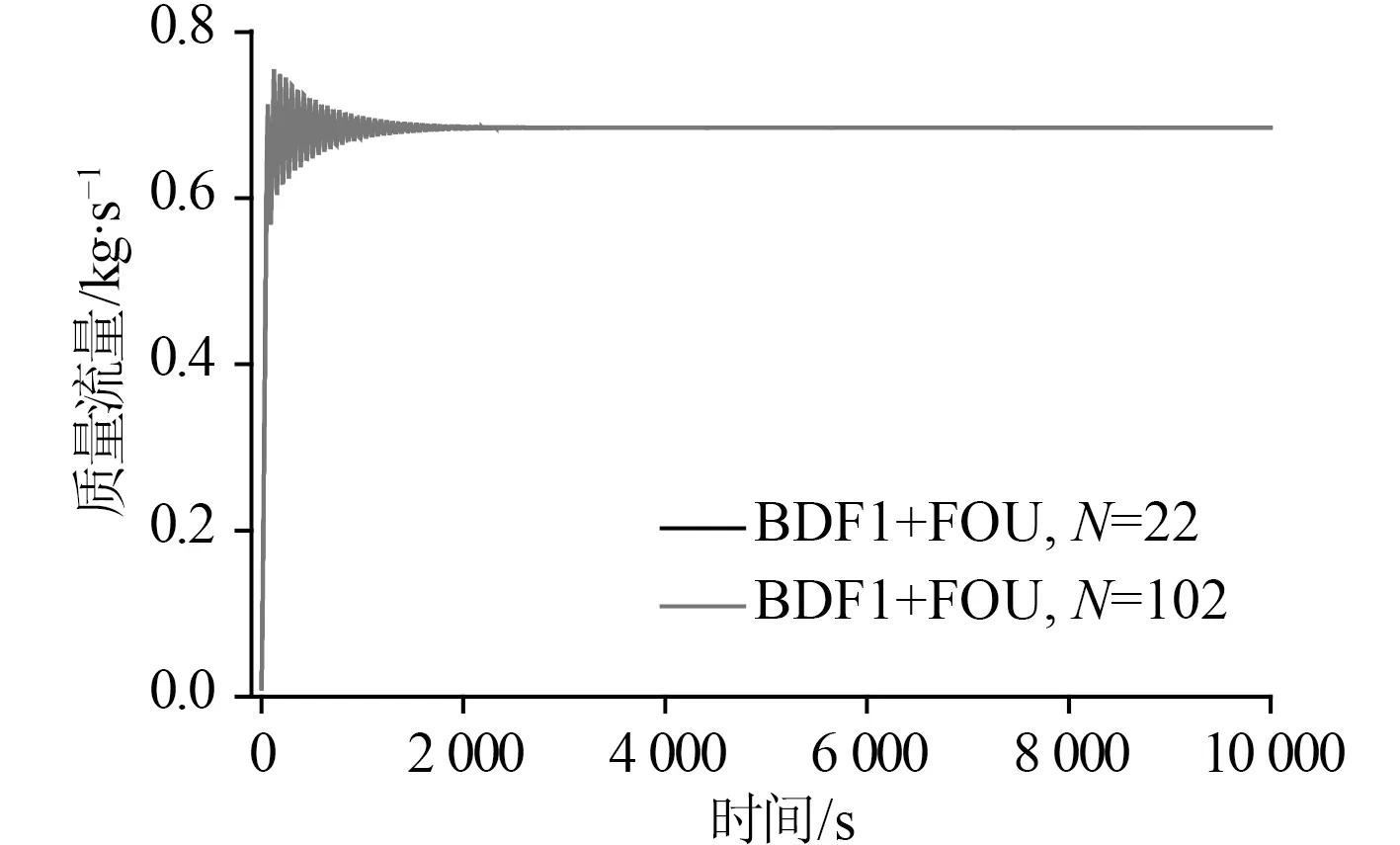
圖11 穩定模式質量流量低階方案的計算結果Fig.11 Calculation results of low order scheme by mass flow of stable mode

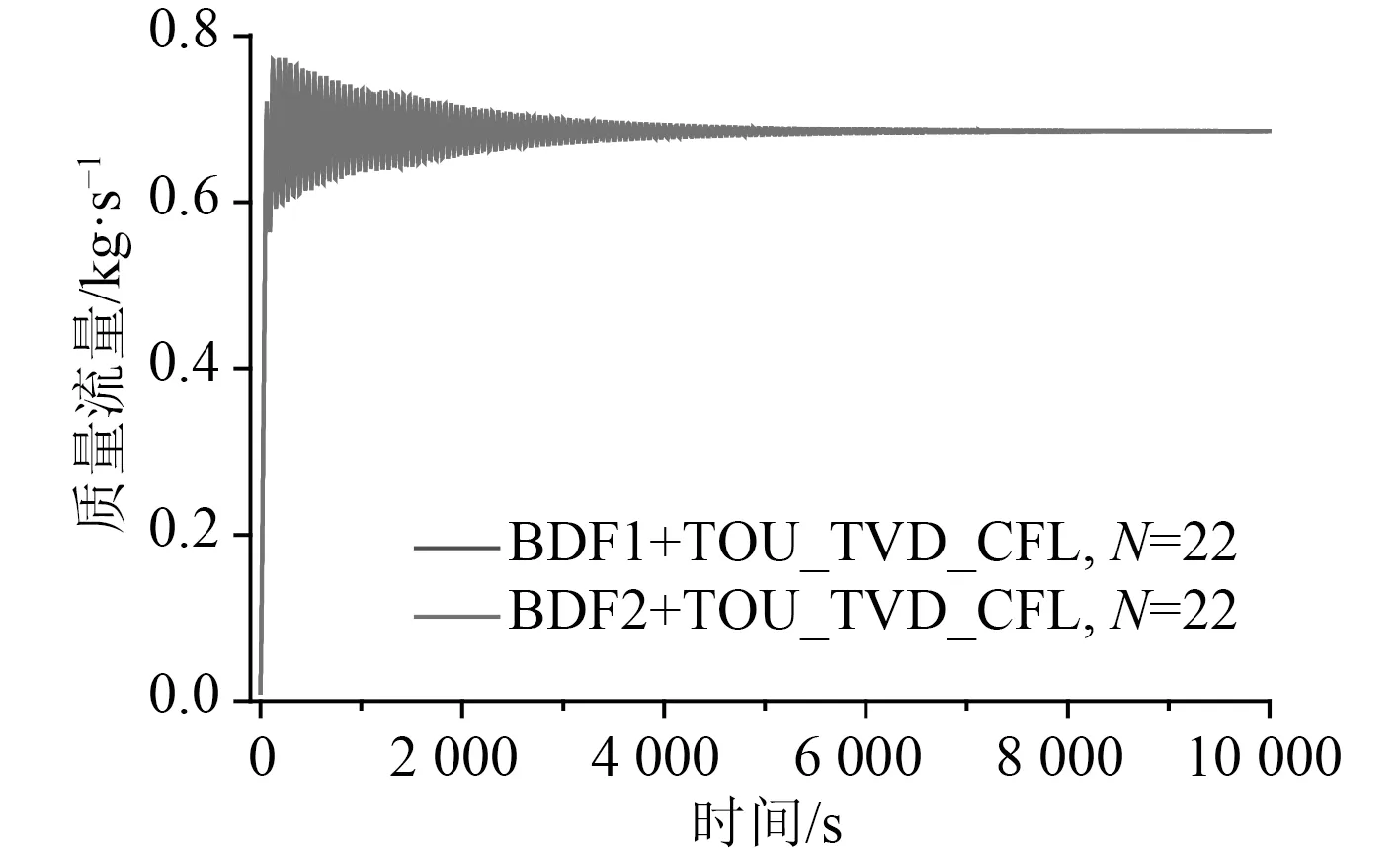
圖12 穩定模式質量流量高階方案的計算結果Fig.12 Calculation results of high order scheme by mass flow of stable mode

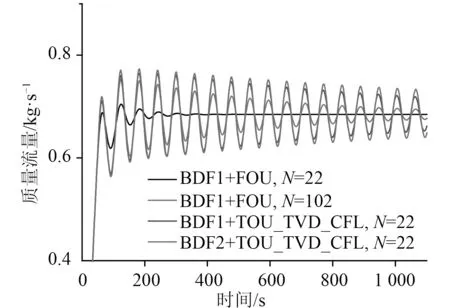
圖13 穩定模式質量流量高階和低階方案的計算結果對比Fig.13 Comparison between low order and high order scheme by mass flow of stable mode

4 結 語

本文采用兩流體雙壓力兩相流模型高精度數值算法對Welander 自然循環的流動不穩定性問題進行計算分析，數值結果表明：高階差分格式可以以較少的網格精確地預測不穩定性邊界和混沌行為，而采用低階差分在網格不夠精細的情況下有可能將自然循環不穩定模式預測為穩定模式，得到錯誤的結果。因此高精度數值解法能有效減小數值擴散，提高自然循環問題的預測精度。