基于帶約束最小二乘的超短基線安裝偏差校準

趙俊波，葛錫云，李 錦，成 月

(中國船舶科學研究中心，江蘇 無錫 214000)

0 引 言

超短基線（ultra short baseline，USBL）系統是一類基于水聲測量技術的定位系統，該類系統由于基陣尺寸小、操作簡單、安裝使用及維修方便，十分適用于母船對水下目標定位。目前，該類系統已在深水潛堤施工、潛水員作業、港灣水下目標探測、海峽電纜管道鋪設、海洋勘探、海洋科學等領域廣泛應用[1–4]。

USBL 定位系統，一般由應答器、聲基陣、母船航姿及定位系統組成。其中，應答器固定安裝在水下目標上，其余設備固定安裝在母船上。超短基線定位系統通過實時測量水下目標相對于母船的相對位置矢量，再結合母船的實時位置信息，實現對水下目標的精確定位。在實際應用時，聲基陣相對于母船的安裝偏差是影響該類系統定位精度的一個重要因素[5–6]。一般來說，1°的首向安裝偏角將會產生1.7%斜距的定位誤差[7]，因此，在使用該類系統進行定位之前，必須先對聲基陣安裝偏差進行校準。

解決超短基線定位系統安裝偏差校準問題的基本方法是最小二乘法[8]，即通過兩組一一對應的觀測數據來擬合參數。由于該校準問題的模型是非線性的，因此通常運用循環迭代的思想來求解[9–12]。唐秋華等[9]提出了基于高斯-牛頓法的安裝偏差校準算法，該方法的有效性在實際工程應用中不斷得到驗證[10–11]。楊保國等[12]比較了高斯-牛頓法、牛頓法、最速下降法等各類循環算法的性能，提出了將循環算法與非循環算法相結合的安裝偏差求解算法。少數學者還根據一些特定應用背景提出了相應的校準方法，江林等[13]根據工程船施工作業特殊性提出了基于太陽時角法的靜態校準方法，Zheng 等[14]針對深海長程超短基線系統提出了基于聲線跟蹤理論的校準方法。

當聲速測量值存在固定測量誤差時，一般需要通過規劃特定的測線軌跡來消除該測量誤差的影響[15–16]。這種處理方式相對費時費力，并且還需要母船循跡航行。針對上述應用背景條件，本文引入帶約束的最小二乘法進行安裝偏差校準，通過在模型上添加適當的系數矩陣，提出一種在聲速測量誤差條件下的校準方法，并通過仿真驗證了本文方法的有效性。

1 超短基線的基本測量原理

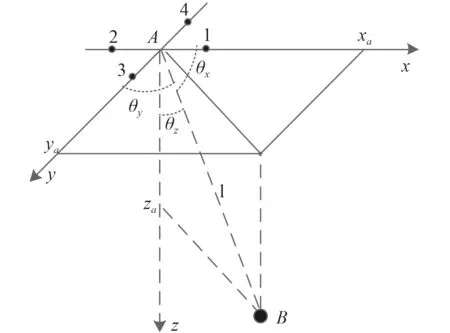
圖1 相對位置矢量示意圖Fig.1 Schematic diagram of relative position vector

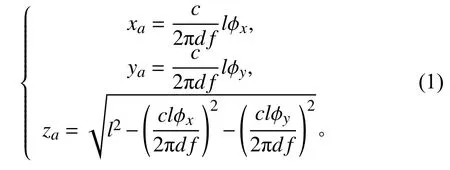
其中，坐標xa,ya,za為相對位置矢量在超短基線聲基陣坐標系（u系）下的投影，l為斜距（這里l=0.5cT，T為聲波往返時間），φx與φy分別為聲基陣端x軸、y軸上的2 組水聽器接收信號的相位差，關于聲基陣坐標系的定義可參見文獻[4]。另外，d為聲基陣對角線長度，f為聲波頻率，c為平均聲速。

2 超短基線安裝偏差的校準方法

2.1 校準問題及其一般求解方法

超短基線定位系統的校準工作主要是完成對聲基陣安裝偏差的估計，其待估計的參數包括聲基陣相對于母船基準位置的安裝角度偏差和聲基陣相對于母船基準位置的安裝距離偏差。

超短基線聲基陣安裝偏差一般采用高斯-牛頓法進行校準。該方法需要2 組測量數據，一組是參考基準值，另一組為測量值，這2 組數據一般會擬定存在某種對應關系（即數學模型），將這2 組數據按照最小二乘準則，完成對模型參數的最優估計。

2.2 基于帶約束最小二乘的校準方法

1）帶旋轉矩陣約束的最小二乘估計法

由參考文獻[18]可知，關于帶旋轉矩陣約束的最小二乘估計法存在如下結論：

引理1

假設m維空間的兩組矢量集X={x1,···,xN}和Y={y1,···,yN}，滿足關系yi=t+cRxi(i=1,···,N)，其中R為旋轉矩陣、t為平移量、c為尺度因子，且令

為方便起見，以下將該方法簡稱為帶約束的最小二乘法。事實上，該方法已在水下航行器聲學多普勒計程儀安裝偏差的在線校準問題上得到了實際應用[19–20]。

2）安裝偏差的校準思路

根據引理1 可知，要估計2 組矢量之間的變換參數，先要知道2 組矢量的觀測值以及矢量之間的對應關系或者模型，然后才能應用該引理求解。

在超短基線系統校準問題中，具體求解思路可總結為：

2.3 聲速測量誤差條件下的處理方法

2）處理方法及校準思路

由于固定聲速誤差對相對位置矢量測量值的x軸和y軸分量的影響是一致的，故考慮將z軸分量的測量值乘以系數m，使得固定聲速誤差對相對位置矢量各分量的影響一致。

3 仿真分析

設母船在水面航行，初始點位置為n系的坐標原點，應答器三維坐標位置為（0 m，20 m，20 m），母船繞應答器航行的軌跡如圖2 所示。假設DGPS 和USBL 的數據采樣頻率均為1 Hz，數據采樣總數為400 對。

圖2 航行軌跡圖Fig.2 Navigation trajectory

假設安裝角度偏差為（3°，2°，5°），安裝位置偏差為（–1 m，0 m，1 m）；設DGPS 的隨機測量誤差服從高斯分布N（0，0.12），USBL 相對位置矢量的隨機測量誤差服從N（0，0.12）和N（0，r2）的高斯混合分布，其中后者以0.05 的概率出現，這里誤差標準差的單位為m；設定聲速真值為1 500 m/s。若將r≥0.3作為存在測量粗差的判據（即認為在r=0.1 時無測量粗差），則可以通過調節r來改變測量粗差的大小。

假設高斯-牛頓法的角度偏差、角度修正量、距離偏差、距離修正量的迭代初值均置零，設定迭代次數為8 次，設4 對樣本點分別為第100 對、第150 對、第250 對和第300 對。

為方便起見，下面將存在固定聲速誤差情形下的校準方法稱為抗固定聲速誤差法。

1)仿真實驗1

本實驗為抗粗差能力測試，假設不存在固定聲速測量誤差。

在抗粗差能力方面，經過多次仿真后發現，當相對位置矢量無測量粗差（對應r=0.1）時，高斯-牛頓法、帶約束最小二乘法和抗固定聲速誤差法的校準精度相當；當相對位置矢量存在測量粗差（對應r=1），特別是在上述4 對樣本點中含有粗差時，高斯-牛頓法的校準結果將出現較大偏差，如表1 所示。然而，粗差的出現對帶約束最小二乘法和抗固定聲速誤差法的校準結果的影響相對較小。可見，帶約束最小二乘法和抗固定聲速誤差法都具有一定的抗粗差能力。

表1 在不同相對位置矢量測量誤差情形下，不同方法的校準結果Tab.1 Calibration results of different methods under different relative position vector measurement errors

2)仿真實驗2

本實驗為抗固定聲速測量誤差能力測試，假設USBL 相對位置矢量無測量粗差。

在抗固定聲速測量誤差能力方面，考慮到固定聲速誤差會使校準結果產生系統誤差，為研究這種系統誤差，特意針對不同的聲速誤差，分別進行100 次仿真模擬，然后將校準結果求平均，得到不同聲速測量誤差條件下的校準結果。

首先，根據仿真結果可知，在不存在固定聲速測量誤差的條件下，3 種校準方法的校準精度相當；當出現10 m/s（或–10 m/s）的固定聲速誤差時，高斯-牛頓法和帶約束最小二乘法的校準結果均受到一定的影響，然而抗固定聲速誤差法的校準結果基本不受聲速測量誤差的影響，如表2 所示。

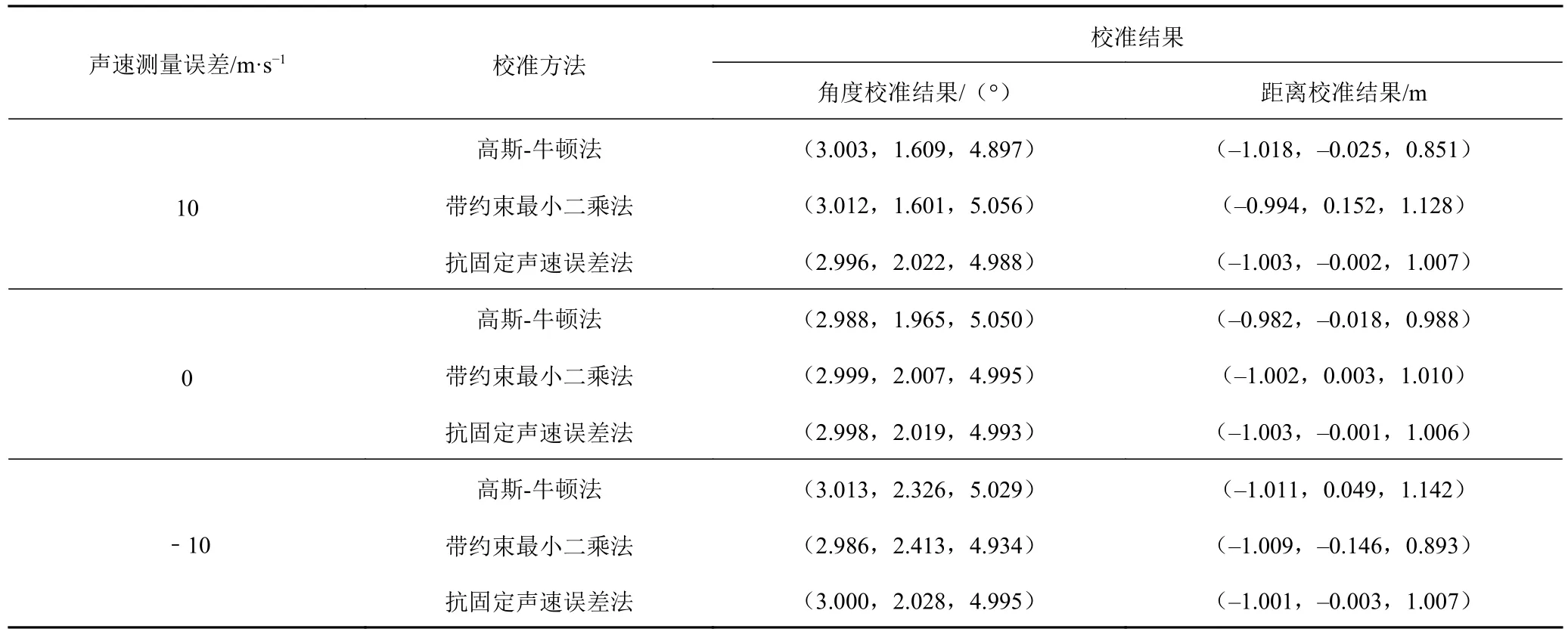
表2 在不同固定聲速測量誤差條件下，不同方法的校準結果Tab.2 Calibration results of different methods under different fixed sound velocity measurement errors

其次，若將角度校準的誤差定義為角度校準結果向量與安裝角度偏差向量的矢量差向量的模，將距離校準的誤差定義為距離校準結果向量與安裝距離偏差向量的矢量差向量的模，將角度校準的誤差和距離校準的誤差統稱為校準誤差，則根據仿真結果可知，當出現一定的固定聲速誤差時（見圖3），固定聲速誤差對高斯-牛頓法和帶約束最小二乘法的影響相對較大，校準誤差隨著聲速測量誤差的增大而逐漸增大，而固定聲速誤差對抗固定聲速誤差法的影響相對較小。

圖3 校準誤差隨聲速誤差的變化曲線Fig.3 Curve of calibration error versus sound velocity error

由此可見，抗固定聲速誤差法具有一定的抗固定聲速測量誤差的能力。

4 結 語

1)針對超短基線安裝偏差的校準問題，提出應用帶約束的最小二乘法來進行校準。仿真結果表明，該校準方法適用于求解超短基線安裝偏差校準問題，并且具有一定的抗粗差能力。

2)在上述校準方法的基礎上。仿真結果表明，該方法具有一定的抗粗差能力和抗固定聲速測量誤差能力，因此，該方法適用于存在固定聲速測量誤差的情況。

本文的校準方法是以聲線為直線傳播為前提的，適用于聲速變化范圍較小的應用場景（比如淺水區）。若用于聲速變化范圍較大的應用場景（如深水區甚至深海），且聲線的初始掠射角偏小，則會導致聲線嚴重彎曲，本文方法不再適用。這里有一種應對思路可供參考：盡量縮小母船的繞行半徑，進而縮小與應答器的水平距離，以增大初始掠射角，降低聲線彎曲程度，使聲線接近直線，以便運用本文方法求解。