旋轉長基線干涉儀“維特比-卡爾曼”濾波定位算法

馬 爽，蔡 凱，劉元華

（北京遙感信息研究所，北京 100011）

0 引言

旋轉長基線干涉儀（RLBI）通過不斷旋轉形成時序上的多條虛擬基線來完成相位差解模糊和定位。與傳統的多通道干涉儀和陣列測向等方法相比，旋轉基線體制具有設備簡單、通道一致性要求低等優點，但是，長基線干涉儀只能測量得到模糊相位差，如何利用模糊相位差高效準確地定位，是旋轉干涉儀定位體制需要解決的首要問題。

要解決該問題，最直接的思路是首先將模糊相位差恢復成真實相位差，再進行定位解算。文獻[1-4]分別研究了圓陣、GPS測向、導彈導引頭測向和近場測向等條件下相位差解模糊的方法，實現了針對具體應用場景的定位解算。但是，該類方法對信號測量間隔和精度要求高，一般需要滿足相對無模糊條件才能實現。為了擴展適用范圍，文獻[5-7]探索了利用模糊相位差直接定位的方法，在定位解空間利用各種優化算法直接搜索最優解。該類方法不再需要恢復真實相位差，但是，計算量隨著可能定位區域的擴大迅速增加，且定位精度與搜索粒度密切相關，在具體應用中受到一定限制。

本文在研究旋轉長基線干涉儀相位差和模糊數變化特點的基礎上，提出了相位差“條帶”和“路徑”的概念，將需要搜索的解空間限制在模糊數序列空間中，與直接在定位空間中搜索相比，大大降低了解空間的維度。用隱馬爾可夫模型（HMM）對“條帶”轉移過程和相位差觀測過程進行建模，通過結合“卡爾曼”濾波過程和“維特比”狀態解碼過程，同步實現了相位差解模糊和濾波定位。該算法能夠對數據進行序貫處理，實時完成解模糊和定位，

定位性能與使用真實相位差進行定位時的“卡爾曼”濾波算法一致。

1 旋轉長基線干涉儀相位差觀測過程HMM模型

旋轉基線通過不斷旋轉來獲取目標在不同基線轉角下的相位差測量值。在旋轉過程中，目標與基線的相對位置不斷變化，對應的模糊數和相位差測量值也隨之改變，這一過程可以用HMM[8]來建模。

1.1 模糊相位差、“條帶”和“路徑”

旋轉基線干涉儀采用單根基線測量信號相位差，真實相位差為：

式中，d為基線長度，λ是信號波長，θ為信號到達方向與基線法平面的夾角。

干涉儀輸出的測量相位差φ′∈(-π,π]，當d＞λ時，存在相位差模糊，測量相位差φ′與真實相位差φ之間滿足如下關系：

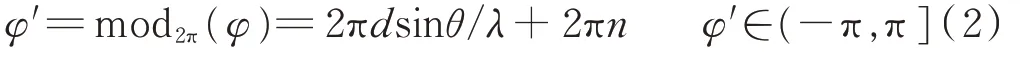
式中，mod2π(·)表示按照2π取模，整數n稱為模糊數。

模糊數n的取值范圍為[-N,N]，N為不超過dλ的整數。例如，當信號頻率為3 GHz、基線長度為1 m時，模糊數的取值范圍為[-10,10]。

假設干涉儀基線在定位區域上方水平放置，定位區域內每個點對應的真實相位差φ、模糊相位差φ′和模糊數n具有如下特點：

1）真實相位差φ連續分布，并沿基線矢量方向單調變化。φ的取值范圍由基線波長比d/λ決定，d/λ越大，取值范圍也越大；基線法平面與定位平面交線對應的相位差為0°。

2）模糊相位差φ′是真實相位差φ向(-π,π]區間內塌縮的結果。由φ＝0的區域向外，每當φ超出(-π,π]范圍時，就加上或減去2π的整數倍，使其值保持在(-π,π]區間中。

3）定位區域被劃分為一系列具有相同模糊數n的區域，區域的邊界由φ′＝π對應等相位差線確定，這些區域按照-N到N的順序沿基線矢量方向依次排列，隨著基線的旋轉不斷變化。

將定位區域上具有相同模糊數的區域稱為“條帶”。隨著基線的旋轉，目標位置所在條帶不斷變化。將每個測量時刻目標所在的條帶n連接起來，就構成了一條“路徑”。圖1顯示一條可能的路徑在條帶空間的變化情況。

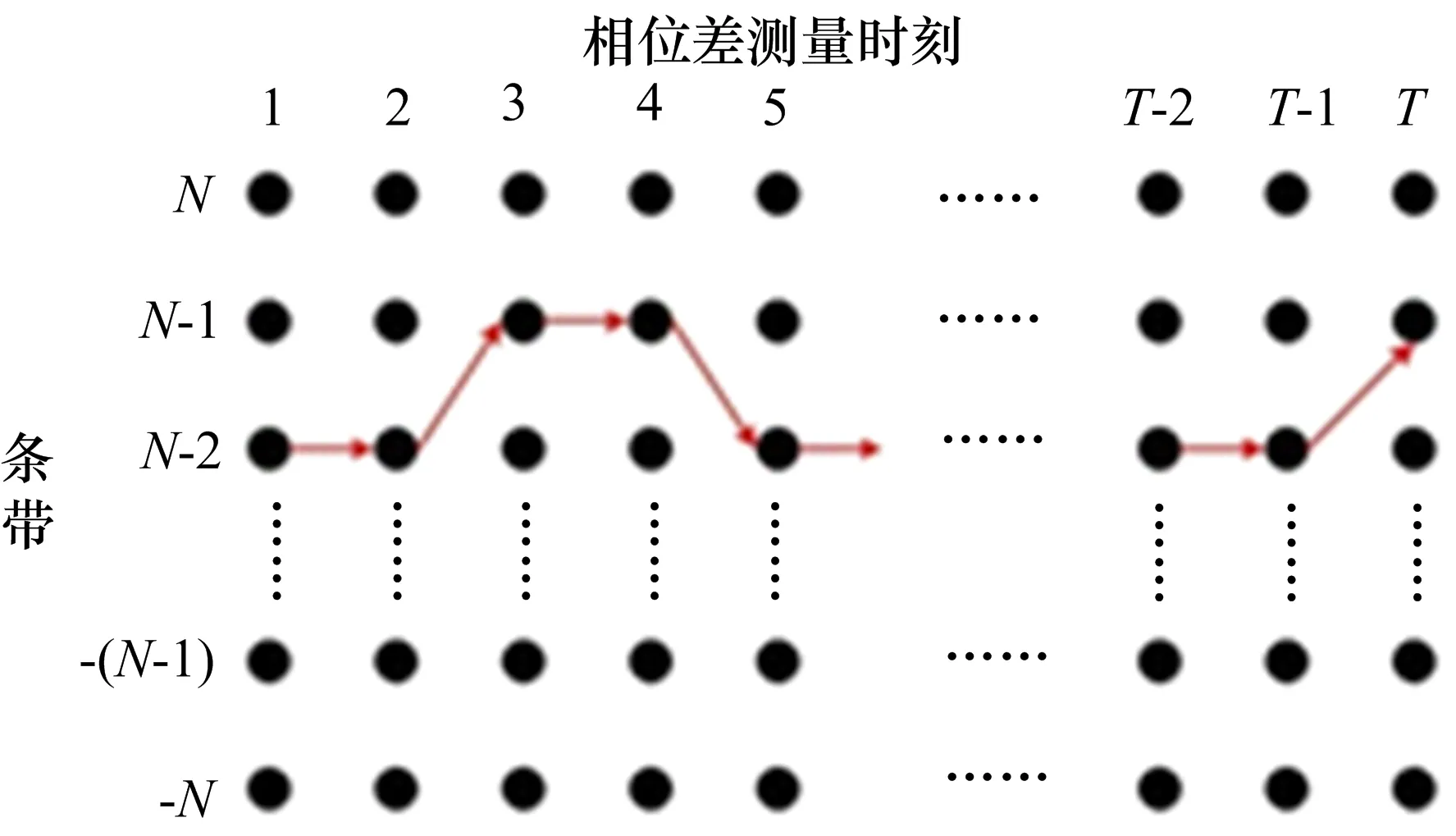
圖1 每個測量時刻目標所在條帶構成的路徑

1.2 觀測過程的HMM模型

目標所在條帶與其位置和基線轉角有關，將條帶作為隱變量，旋轉基線相位差序列的觀測過程可用HMM來描述。

HMM是一種時序的概率模型，描述由一個隱藏的馬爾可夫鏈隨機生成不可觀測的狀態隨機序列，再由各個狀態生成一個觀測而產生觀測隨機序列的過程，其中隱藏的隨機序列稱為狀態序列,觀測產生的隨機序列稱為觀測序列。

設Q＝{q1,q2,q3,…,q K}代表所有狀態的集合，V＝{v1,v2,v3,…,v M}代表所有可能觀測的集合，HMM可由如下三元組來描述：

式 中，A＝[aij]K×K為 狀 態 轉 移 概 率 矩 陣，aij＝P(st＋1＝qj|st＝qi)表示從時刻t到時刻t＋1由狀態qi轉移到狀態qj的概率；B＝[bij]K×M為觀測概率矩陣，bij＝P(ot＝v j|st＝qi)表示時刻t在qi狀態下觀測到v j的概率；Π＝[πi]K×1為初始狀態概率向量，πi＝P(s1＝qi)代表t＝1時刻處于狀態qi的概率。

具體到旋轉基線干涉儀定位的情況，目標所在條帶n是不可觀測的隱藏狀態，狀態集合Q＝{-N,-(N-1),…,N-1,N}。觀測集合對應相位差測量值，是(-π,π]之間的連續變量。狀態轉移矩陣A用于描述基線旋轉導致的目標在各“條帶”之間的轉移概率。觀測概率矩陣B表示目標位于某一“條帶”時觀測到測量相位差的概率。Π代表目標位置最初所在條帶的概率。

由上文可知，任意一條“路徑”對應一個狀態序列s1s2s3…sT，如果能夠由測量相位差序列o1o2o3…o T推斷出目標真實位置對應的狀態序列，就實現了相位差解模糊。

接下來，通過將“卡爾曼”濾波(Kalman filtering)過程嵌入到“維特比”算法(Viterbi algorithm)中，同步實現相位差動態解模糊和濾波定位。

2 “維特比-卡爾曼”濾波定位算法

2.1 假設真實相位差已知情況下的“卡爾曼”濾波定位過程

“卡爾曼”濾波[9]是一種經典的遞歸濾波器，典型應用是從一組包含噪聲的觀測序列中預測物體的運動狀態。在旋轉干涉儀定位中，假設真實相位差已知，卡爾曼濾波定位過程如下。

1）狀態方程和觀測方程

為了討論方便，假定目標固定不動，對應的狀態方程為：

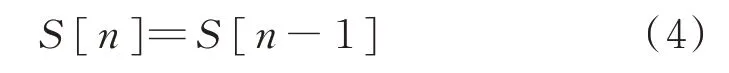
狀態S＝rT，rT＝[x y z]T是目標的直角坐標矢量。

假設能夠測量到真實相位差φ，觀測方程為：φ＝

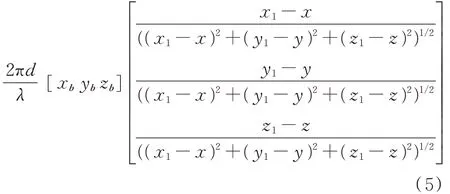
式中，d為干涉儀基線長度，b＝[x b yb zb]T為單位基線矢量，r1＝[x1y1z1]T是干涉儀所在位置的直角坐標矢量。

2）卡爾曼濾波過程

根據以上的狀態方程和觀測方程，卡爾曼濾波的具體過程如下。

預測：

最小預測均方誤差(MSE)矩陣：

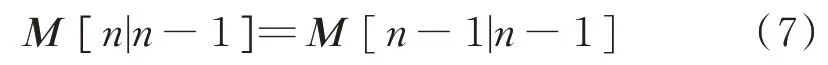
卡爾曼增益：

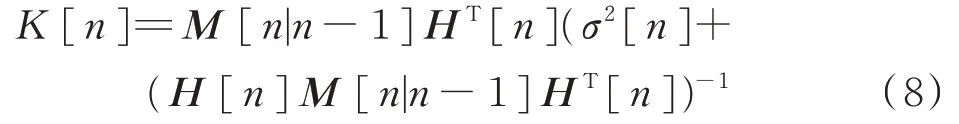
修正：

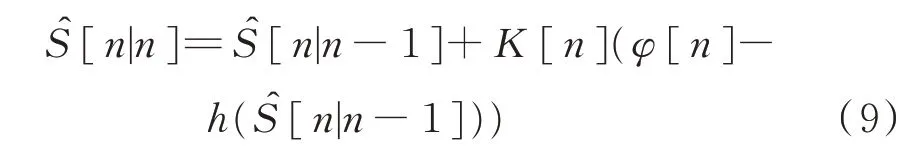
最小MSE矩陣：

式中，σ2[n]為真實相位差φ的測量噪聲方差，H[n]為觀測方程φ＝h(S)的雅克比矩陣

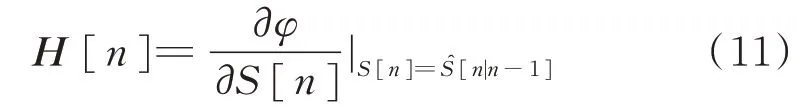
濾波過程中v(n)＝φ[n]-h(S?[n|n-1]稱為“新息”，表示觀測值與預測值的差。

令?[-1|-1]等于目標的初始位置[x0y0z0]T，M[-1|-1]等于目標初始位置方差矩陣為相位差φ的觀測方差，通過遞歸計算，就可以得到對系統狀態S的估計。

3）雅克比矩陣H[n]的推導

雅克比矩陣H[n]是真實相位差φ關于目標位置rT＝[x y z]T的導數：

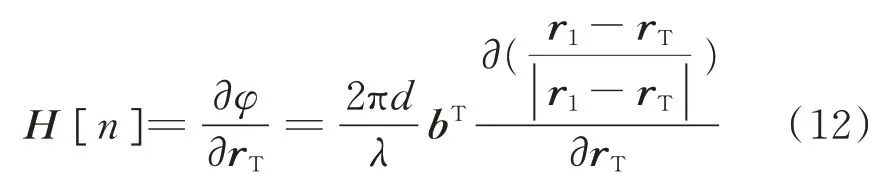
式中，

令：

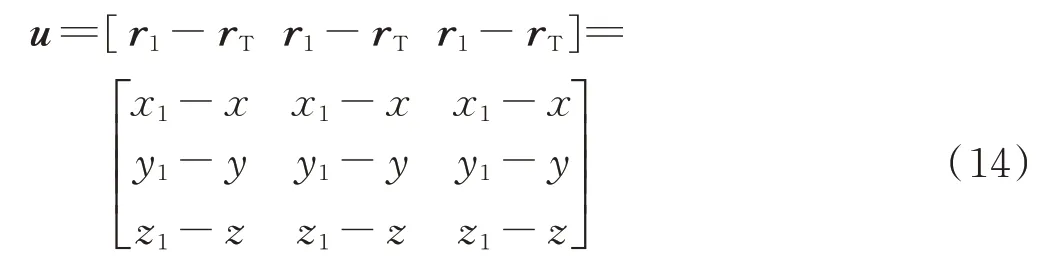
得：

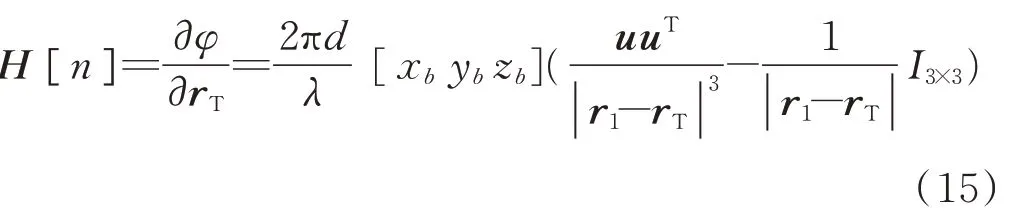
以上是假設真實相位差φ已知情況下的卡爾曼濾波過程，但實際中干涉儀只能輸出測量相位差φ′，要完成濾波定位過程，就需要實時解出目標所在的條帶n，接下來，通過引入“維特比”算法來解決這一問題。

2.2 “維特比”算法解碼最大概率路徑

“維特比”算法是HMM模型中根據觀測序列解碼狀態序列的標準算法。給定觀測序列o1o2o3…o T，要找出最可能的狀態序列s1s2s3…sT，使式（16）中的條件概率最大：

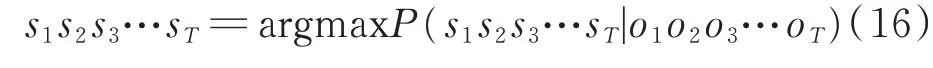
根據馬爾可夫齊次性假設和觀測獨立性假設，等價于:

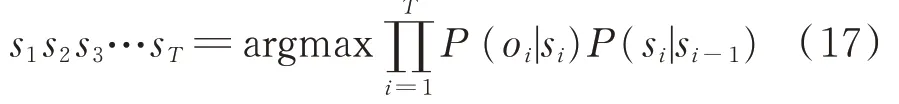
如果直接計算式（17），計算復雜度將是O(K T)，式中,K為狀態數，T為序列長度，計算量非常大。“維特比”算法通過在“籬笆網絡（Lattice）”中應用動態規劃技術，將計算復雜度降低為O(TK2)，有效解決了狀態解碼問題。

圖2給出了籬笆網絡的結構。路徑在網絡中從左向右傳播，由于所有路徑必然經過網絡中的每一列，且如果最大概率路徑經過節點X ij，那么該路徑上從起始時刻到第i個時刻的部分路徑也必然是該時段所有路徑中的最大概率路徑。因此，在任一時刻t，只要考慮K條最大概率路徑即可[10]。

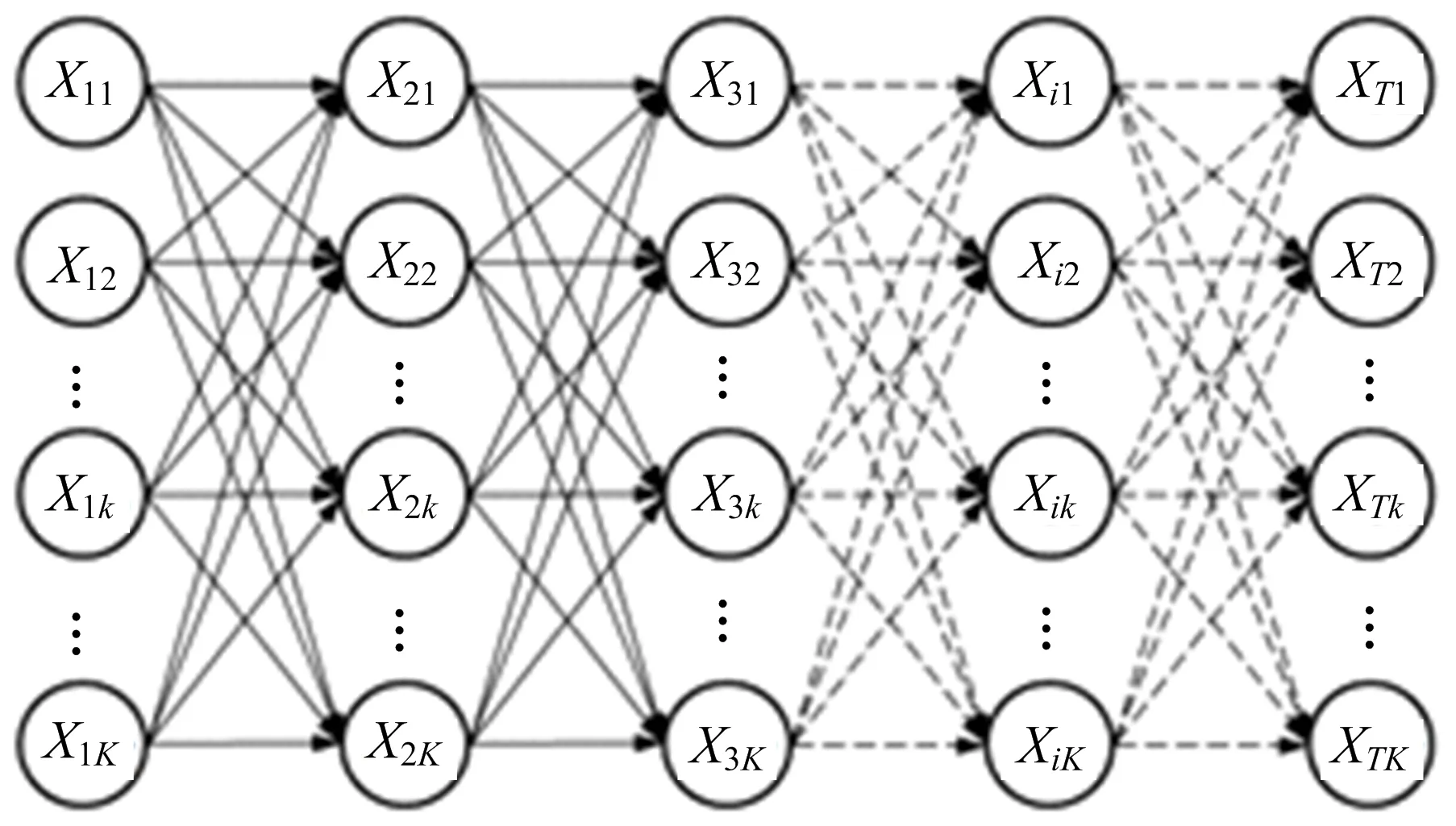
圖2 籬笆網絡（Lattice）的結構

基于以上性質，籬笆網絡中最大概率的路徑的計算過程如下：

1）初始化。計算第一列各狀態節點的初始概率δ1，并記錄每個節點前一時刻的狀態ψ1：

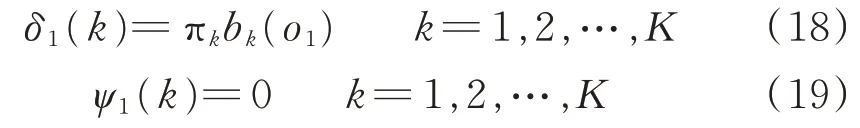
式中，πk為狀態k的初始概率，bk(o1)為狀態k條件下觀測到o1的概率。由于第一列沒有前一時刻，因此ψ1(k)統一記為0。

2）遞推。對于t＝2,3,…,T，根據下式遞推計算籬笆網絡中每一列的K個節點的概率δt，并記錄每個節點前一個時刻的狀態ψt：

式中，ajk為狀態j轉移到狀態k的概率，bk(ot)為狀態k條件下觀測到ot的概率。

3）終止。當遞推到達時刻T后，遞推終止，此時，按照下式計算最優路徑概率P*和最優路徑的最后一個狀態k*T：

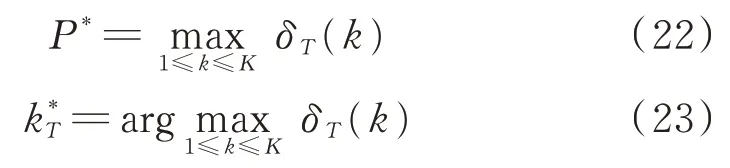
4）回溯。找到最優路徑的最后一個狀態k*T后，根據下式回溯出最大概率路徑：

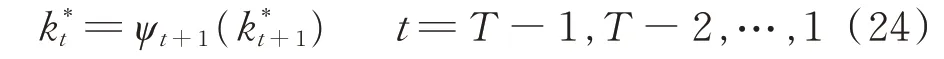
最后求得最大概率路徑I*：

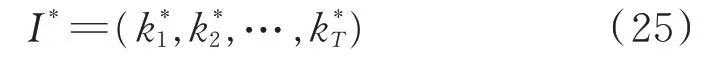
接下來，通過將“卡爾曼”濾波步驟嵌入到“維特比”算法過程中，擴展上述遞歸過程，完成狀態轉移概率A＝[aij]K×K和觀測概率B t＝[bi(ot)]K×1的計算，同步實現旋轉基線干涉儀相位差解模糊和濾波定位。

2.3 “維特比-卡爾曼”濾波過程

2.3.1 初始化籬笆網絡和濾波狀態

根據式（18）、式（19），初始化籬笆網絡的狀態，由于目標的位置未知，信號到達的初始時刻基線的旋轉角度也是隨機的，因此，可以簡單地認為目標位于各個條帶的概率是相等的，即πi＝1/k,i＝1,2,…,K。同樣，由于目標在條帶中的具體位置未知，觀測概率的最初狀態概率也認為是相等的，bk(o1)＝1/k,i＝1,2,…,K，因此：

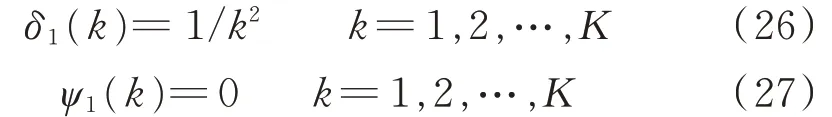
在籬笆網絡中，初始時刻的每個狀態代表目標所在的條帶，也就是可能的模糊數n∈[-N,N]。根據測量相位差φ′和模糊數n可以恢復出K＝2N＋1個可能的真實相位差φ(k)，利用φ(k)根據式（6）-（10）執行一步濾波定位，得到初始時刻每個狀態下的一次定位位置S1(k)和最小均方誤差矩陣M1(k)。

2.3.2 遞推計算濾波位置和最大概率路徑

注意到“卡爾曼”濾波和“維特比”最大概率路徑計算過程都采用遞歸的方式計算，將2種過程融合在一起，用籬笆網絡的狀態k將測量相位差φ′轉換為真實相位差φ(k)，用其進行一步濾波定位，同時，用該濾波定位結果對應的估計相位差φ?(k)與真實相位差φ(k)之間的相似程度來計算觀測概率，完成一步遞歸計算，具體步驟如下：

1）執行一步濾波定位

對于籬笆網絡中的節點X tk，利用該節點對應的模糊數n將測量相位差φ′t轉換為真實相位差φt(k)：

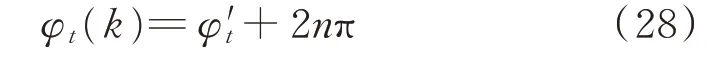
分別以t-1時刻的K個節點對應的濾波位置St-1(k)，k＝1,2,…,K和 最 小 均 方 誤 差 矩 陣M t-1(k),k＝1,2,…,K為狀態，φt(k)為觀測值，根據式（6）-（10）執行一步濾波定位，得到節點X tk下的K個 濾 波 位 置Stk(j),j＝1,2,…,K和M tk(j),j＝1,2,…,K。

2）計算狀態轉移概率

狀態轉移概率矩陣A＝[aij]K×K，其中aij表示隨著基線的旋轉，在相鄰時刻目標在從條帶i轉移到條帶j的概率。根據在時刻t對系統狀態了解程度的不同，按照以下幾種情況來計算狀態轉移概率。

①無任何先驗知識的情況

在目標位置無任何先驗知識，且時刻t-1到t之間的時間間隔隨機產生的情況下，隨著基線的旋轉，目標位置可能在任意2個條帶之間轉移，此時，可以簡單認為轉移概率是平均分布的，即：

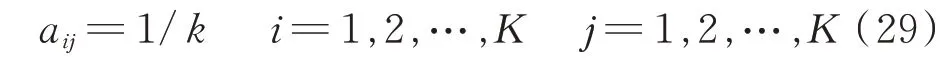
②目標粗略位置已知的情況

假設已經獲取了目標的粗略位置，例如在濾波定位過程中不斷接近目標真實位置，那么，在t-1時刻，根據位置利用式（2）和式（5）可以估計出目標可能的條帶范圍，例如連續的3個條帶(i-1,i,i＋1)，基線旋轉到t時刻，同樣可以計算出另一個可能的條帶范圍，例如(j-1,j,j＋1)，這樣，從t-1時刻到t時刻，轉移概率可以表示為：

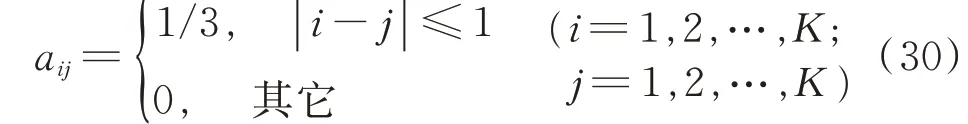
具體的條帶范圍需要根據估計位置與真實位置的接近程度來設置，越接近，則可能的條帶范圍越小，否則，需要給多個可能的條帶賦予非零概率。

③相對相位差無模糊的情況

當t-1和t時刻的真實相位差滿足|φt-φt-1|≤π時，稱為相位差相對無模糊。此時，可以恢復出測量相位差φ′t＋1和φ′t之間真實的差值。文獻[1]中證明，當|Δω|≤2arcsin(λ(4d))時，干涉儀覆蓋范圍內任意位置的相位差相對無模糊。此時，轉移概率可以表示為：

當φ′t-φ′t-1≤-π時，

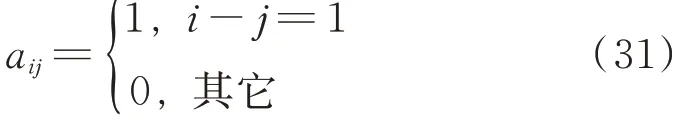
當φ′t-φ′t-1＞π時，

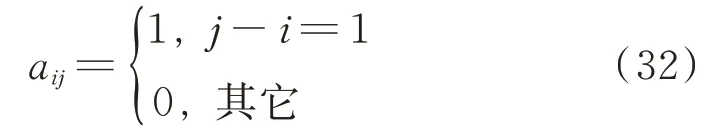
當-π＜φ′t-φ′t-1≤π時，

3）計算觀測概率

觀測概率bk(ot)表示t時刻在狀態k下觀測到ot的概率。相位差是由位置決定的，經過一次濾波后，在節點X tk下有K個濾波位置Stk(j)，j＝1,2,…,K，根據式（5）可計算出對應的K個相位差：

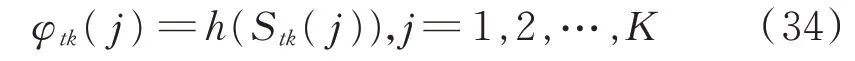
將φtk(j)與真實相位差φt(i)之間的相似程度作為計算觀測概率bk(ot)的依據。首先利用sigmoid函數將φtk(j)-φt(i)變換到(-1,1)的范圍內：

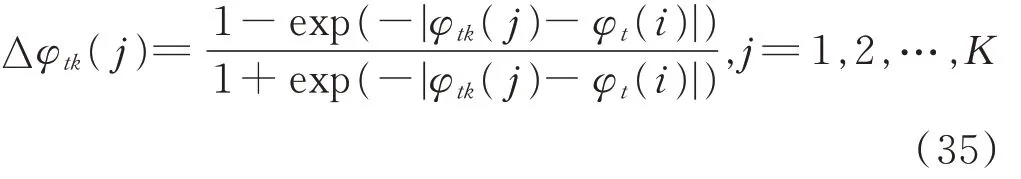
然后按照標準正態分布計算觀測概率：

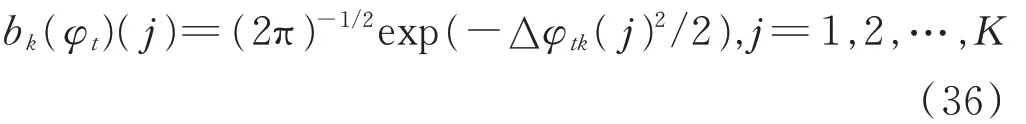
4）保存最大概率狀態

對于進入節點X tk的K條路徑，選取當前最大的部分路徑概率對應的一條作為X tk的狀態。根據下式計算籬笆網絡中時刻t的K個節點的概率δt，并記錄每個節點前一個時刻的狀態ψt：

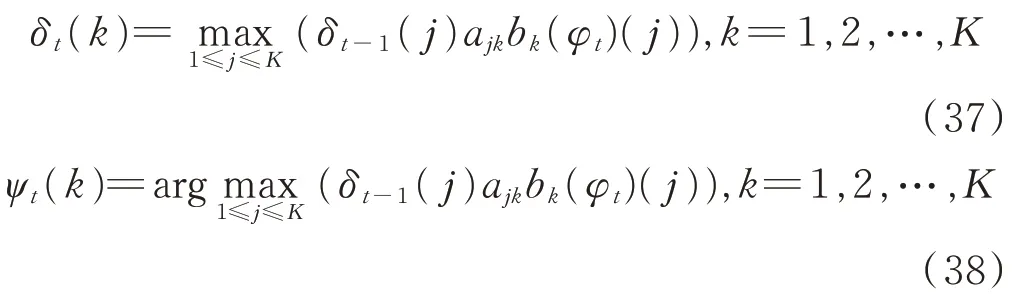
記錄最大概率路徑對應的濾波位置和最小均方誤差矩陣：

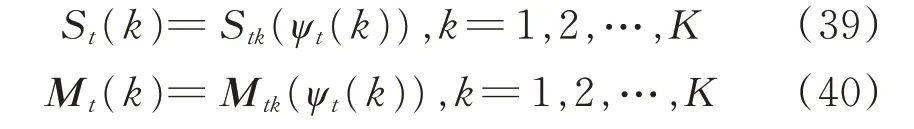
5）遞歸終止和路徑回溯

當遞推到達時刻T后，遞推終止，此時，按照下式計算最優路徑概率P*、最優路徑的最后一個狀態k*T和濾波定位位置S*T：

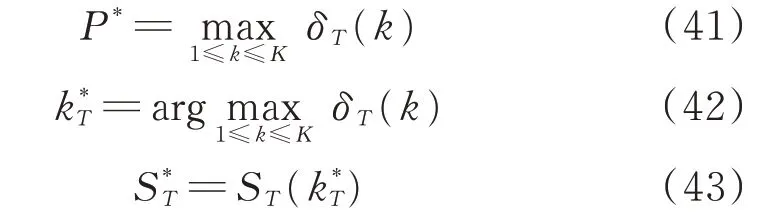
找到最優路徑的最后一個狀態k*T后，根據下式回溯出最大概率路徑：

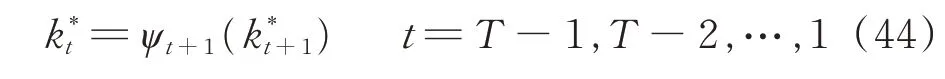
最后求得最大概率路徑I*：

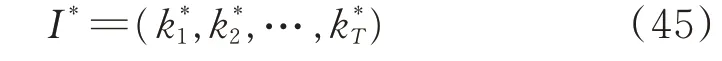
至此，完成了“維特比-卡爾曼”濾波定位的全過程。該算法利用“維特比”算法根據測量相位差序列解碼最優路徑，相當于解出每次測量時對應的模糊數，從而利用真實相位差完成濾波定位。定位性能方面與“卡爾曼”濾波一致，此處不再贅述。

3 仿真分析

仿真場景設置如下：目標位置的經緯度為[123.117 5°,23.553 1°]，旋 轉 基 線 位 置 的 經 緯 度 為[125°,28°]，在500 km高度水平放置，基線長度為2 m，按照360°/s的速度旋轉。輻射源信號脈沖重復間隔在[1 000μs,10 000μs]區間內隨機選取，脈沖列長度為100。濾波初始位置經緯度隨機選取為[124.132 7°,22.080 9°]。

采用“維特比-卡爾曼”濾波算法進行處理，經過100步濾波后得到定位位置的經緯度為[123.114 7°，23.551 3°]，定位誤差為351 m，與利用真實相位差進行卡爾曼濾波后的定位結果一致。濾波定位每一步的結果如圖3所示。其中，圖3(a)給出了濾波定位過程中估計位置不斷接近真實位置的情況；圖3(b)是濾波過程中最大概率路徑對應的相位差“新息”的變化情況，可見，隨著濾波的進行，相位差“新息”在不斷減小，說明估計相位差與真實相位差越來越接近；圖3(c)給出了籬笆網格中由最終狀態回溯的所有路徑（13條）的每一步的定位結果，可見，非真實路徑對應的定位結果始終是發散的，而真實路徑對應的結果逐漸收斂到真實位置（紅色星號）；圖3(d)給出了在維特比遞推過程中籬笆網絡中每一列最大概率的變化情況，可見，隨著遞歸的進行，真實路徑上的概率比重不斷增加，而其它路徑上的概率由于采用了錯誤的相位差進行濾波，無法收斂到真實位置，導致概率比重逐漸減小，通過選取最大概率的狀態并回溯后，找出真實路徑，從而實現相位差解模糊和定位。

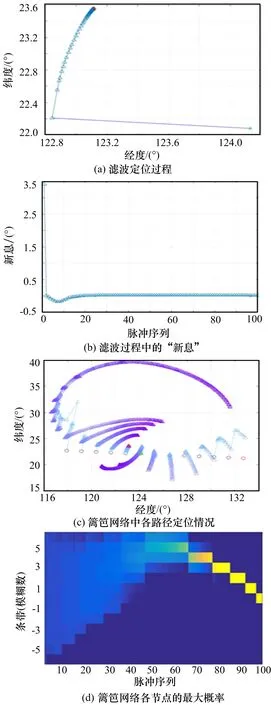
圖3 “維特比-卡爾曼”濾波算法一次仿真中的定位過程

4 結束語

本文研究了旋轉長基線干涉儀利用模糊相位差直接定位問題。首先用HMM對旋轉基線定位過程建模，利用維特比算法根據測量相位差解碼模糊數序列，在籬笆網格計算過程中引入卡爾曼濾波步驟，同步計算目標估計位置和最優路徑概率，解碼最優狀態序列，實現了利用模糊相位差直接濾波定位。最后用仿真實驗驗證了算法的有效性。■