淺析非對稱雙列向心球面滾子軸承基本額定動載荷的計算方法

唐麗虓

（瓦房店軸承集團有限責任公司 精密事業部 遼寧 瓦房店 116300）

1 前言

Lundberg 和 Palmgren 所建立的額定動負荷理論是滾動軸承疲勞壽命計算的基礎。目前，國際標準ISO281 Rolling bearing — dynamic load ratings and rating life[1]所規定的多列滾動軸承基本額定動負荷的計算方法是在基于多列同性的基礎上進行了簡化，本文將從滾動軸承滾動疲勞壽命計算的基本原理入手，對兩列滾動體尺寸及接觸角都不同的雙列向心球面滾子軸承的額定動載荷的理論計算方法進行簡要的分析。

2 理論分析

令Si表示內圈的使用概率；Se表示外圈的使用概率；S表示整個軸承的使用概率，應用線接觸向心滾子軸承疲勞壽命基本公式， 由概率乘積法則推導出計算兩列滾動體尺寸及接觸角都不同的雙列向心球面滾子軸承（簡稱：非對稱雙列向心球面滾子軸承）基本額定動負荷的通用形式。

3 非對稱雙列向心球面滾子軸承基 本額定動負荷的一般形式

非對稱雙列向心球面滾子軸承基本結構參見圖 1。

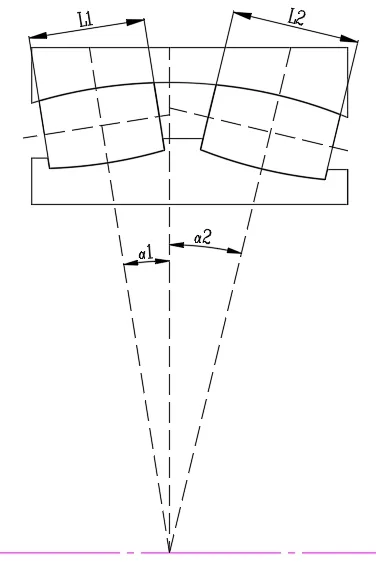
圖1 非對稱雙列向心球面滾子軸承

由概率乘積法求滾動軸承的額定動負荷，因為滾動體負荷Q與軸承負荷Fr成正比，在線接觸疲勞壽命基本公式中，

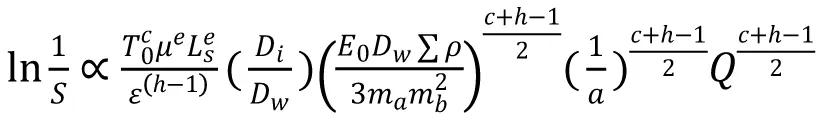
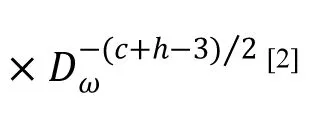
因為滾動體負荷Q與軸承負荷Fr成正比，將其中的Q換成Fr并保留Le項，其余各項用ki表示，則有

對于線接觸，ω=（c-h+1）/2

式中：

c——Hertz 壓縮常數量，單位接觸長度的 量，常數

h——油膜厚度，常數

e——軸向負荷影響系數，常數

Q——作用在滾動體上的負荷

Lundberg-Palmgren 試驗得出的e、c、h常數值如下：

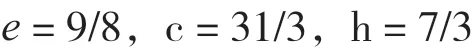
當Si=0.9 時,L= 1 (百萬轉)，此時的外負荷Fr為內圈的額定動負荷Ci，即Fr=Ci。

式（1）成為

同理可得，

對整個軸承而言，用概率乘積法則，S=SeSi，即

當S= 0.9，L= 1（百萬轉）時，此時的Fr為整個軸承的基本額定動負荷Cr,

即Fr=Cr。由式（1）和（3）可得：

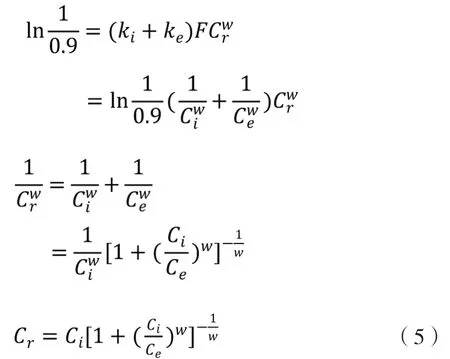
式（5）為內、外圈的額定動負荷與整個軸承的額定動負荷之間的關系。必須指出，令Si= 0.9 及Se = 0.9 時，是為了計算內、外圈各自的使用概率計算系數ki及ke。Palmgren 在計算整個軸承的使用概率時，用S=SeSi, 但此時的Si及Se一定要大于 0.9，使其乘積為 0.9。

式（5）是單列滾動軸承額定動負荷的計算方法，本文涉及的軸承結構為兩列滾子軸承，軸承的滾動體列數i= 2，假設每列滾動體所擔負的徑向負荷相等，軸承所承受總的徑向負荷為Fr，則每列承受Fr/2，整個軸承的使用概率是各列使用概率的乘積。用腳標Ⅰ、Ⅱ分別表示軸承中第一列和第二列，CⅠ和CⅡ分別表示各列的額定動負荷，Cr表示整個軸承的基本額定動負荷。式（1）的表達方式，有

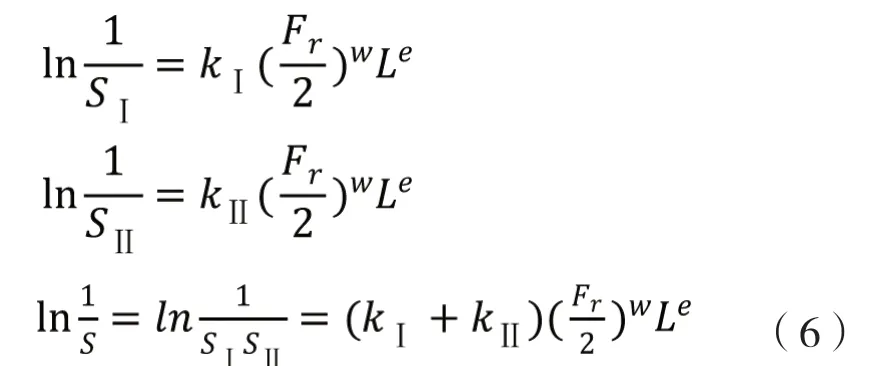
Palmgren 認為SⅠ=SⅡ=Si=0.9。當L= 1時，Fr=C；在計算kⅠ及kⅡ時，L= 1，式（6）的Fr/2 分別為CⅠ和CⅡ。

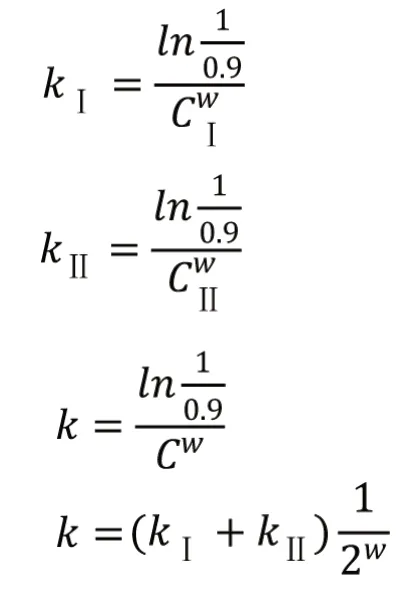
由式（7）可得

Cr為非對稱雙列向心球面滾子軸承的基本額定動載荷。

4 內圈和外圈的額定動負荷

在徑向負荷或徑、軸向負荷同時作用時，軸承內各滾動體所承受的負荷是不相同的。若內圈旋轉，外圈靜止，分別考慮內、外圈的額定動負荷。

4.1 內圈的額定動負荷 Ci

線接觸時, 內圈的額定動負荷為：

將滾動體額定負荷簡化的公式

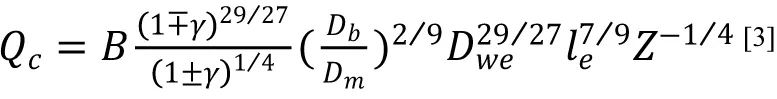
注：上式中的上面的符號適用于內圈，下面的符號適用于外圈。常數 B 由材料決定。對于標準的軸承鋼制滾動軸承，額定滾動體負荷以牛頓為單位，實驗給出 B = 551.15。

代入（9），可得

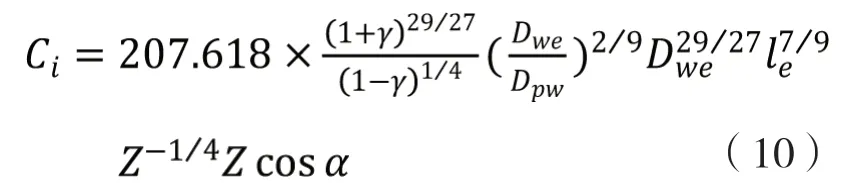
式中 γ——由滾動體直徑、接觸角和軸承平均直徑所確定的結構參數，非對稱雙列向心球面滾子軸承的

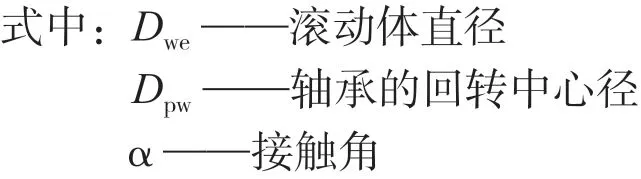
4.2 外圈的額定動負荷 Ce

線接觸時,外圈的額定動負荷為：

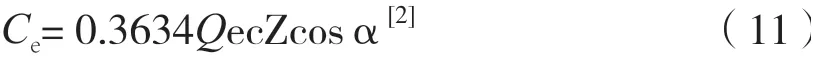
將滾動體額定負荷簡化的公式

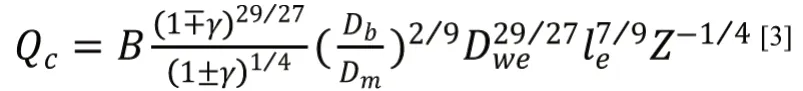
代入（11），可得

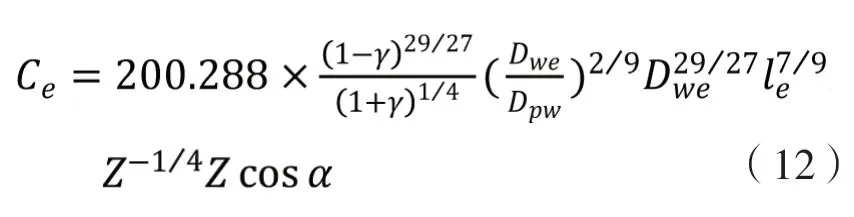
使用式 （10） 和 （12）和（5）可以分別計算出不同設計參數的每一列軸承的基本額定動載荷，再使用式（8）計算出整個軸承的基本額定動負荷。

5 校核實例

以 240/600 該規格為例，Scheaeffler 代號：F-630663.PRL

外形接口尺寸：d = φ600mm, D = φ870mm, B = 272mm

設計結構參數：e1= 0.23, e2 = 0.36，Z = 2*34

額定動載荷：Cr= 8 200 kN

以相同的設計結構參數進行非對稱雙列調心滾子軸承的基本額定動載荷的計算，計算結果為8 219kN。

利用仿真計算軟件對該規格的雙列調心滾子軸承的基本額定動載荷進行了校核，結果為 8 190 kN。

6 結束語

本文針對非對稱雙列調心滾子軸承的基本額定動載荷的計算方法進行了簡要的推理，與 FAG的同規格非對稱雙列調心滾子軸承的基本額定動載荷數值進行對比，數值基本一致，說明本文中的計算方法與國際先進軸承制造廠商所使用的方法基本一致。本文為非對稱雙列調心滾子軸承的基本額定動載荷的計算提供了參考方法。