基于改進粒子群算法求解分布式多工廠生產調度問題
王仕存,唐敦兵,朱海華,聶慶煒,潘俊峰,楊雷
(1. 南京航空航天大學 機電學院,江蘇 南京 210016;2. 江蘇天安智聯科技股份有限公司,江蘇 無錫 214171)
0 引言
隨著云制造[1]和生產全球化的不斷發展,基于云平臺的大規模協同制造漸漸成為國內外制造業研究的重點。在此背景下,傳統集中式制造工廠漸漸向分布式工廠轉變[2]。隨著工廠數目的增多,傳統的車間調度已難以滿足云平臺的需要。如何對各個分布式工廠的生產任務進行合理有效的調度,已成為當前迫切需要解決的問題。
近年來,國內外對分布式多工廠生產調度問題(distributed multi-plants production scheduling problem,DMPPSP)進行了相關的研究。根據車間之間是否存在交互,本文將每個工廠劃分為多個獨立的柔性制造單元(flexible manufacturing unit,FMU),把DMPPSP轉化為分布式柔性車間調度問題(distributed and flexible job shop scheduling problem, DFJSP),從而解決了DMPPSP的問題。
由于該問題包含柔性作業車間調度問題(flexible job shop scheduling problem, FJSP),屬于NP-hard問題[3],目前研究多采用智能優化算法進行求解。在國外,CHAOUCH I等[4]在混合蟻群算法的基礎上提出了一套新型的動態調度規則,高效求解了DMPPSP;MARZOUKI B等[5]為了得到最小化、最大完工時間,采用了基于化學反應優化的元啟發式算法進行求解;在國內,吳銳等[6]設計了一種包含三維向量的編碼方案,運用改進人工蟻群算法提升了算法的局部搜索能力。這些研究都在一定程度上解決了DMPPSP,但其算法多數存在不確定性大、易陷入局部最優解的缺陷。
本文將DMPPSP轉化為DFJSP,提出了一種改進的混合粒子群算法,提高了全局搜索能力,實現了以最小化、最大完工時間為目標的分布式多工廠生產調度問題的求解。
1 分布式柔性車間調度問題
1.1 符號描述
文中使用的符號含義如表1所示。

表1 符號含義表
1.2 問題描述
問題描述:云平臺上存在工件類型集合為T={T1,T2,…,Tt}的待加工工件集合J={J1,J2,…,Jn},需要將J中的工件分配至FMU集合U={U1,U2,…,Ur}進行加工,其中各個FMU與倉庫中心的距離集合為H={H1,H2,…,Hr}。每個FMU有多個加工機器Mu={Mu,1,Mu,2,…,Mu,lu},每個工件加工過程共分為pi道工序。
由上述描述可知,DFJSP分為3個子問題,即FMU選擇、機器選擇和工序選擇,如圖1所示。
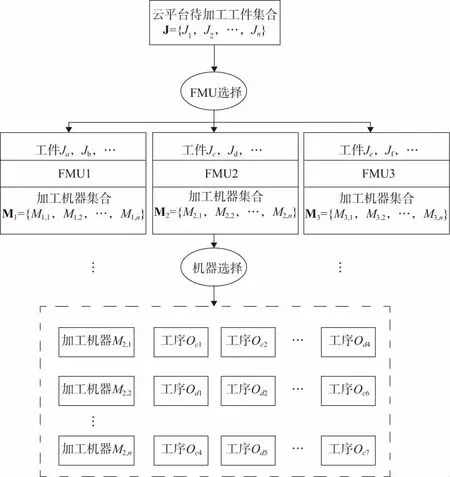
圖1 DFJSP示意圖
1.3 模型建立
本文模型基于的假設如下:
假設1:在初始時刻,待加工工件集合確定,FMU內任何機器都可用;
假設2:每個FMU都能加工任意類型的工件,每個工件只能分配至一個FMU;
假設3:每個機器在某一時刻只能最多加工一個工件;
假設4:每個工件的某個工序只能被某個機器連續獨立加工完成;
假設5:同一個FMU內的同類型加工機器對同一道工序的加工效果相同。
基于以上假設,本文建立了以最小化、最大完工時間為目標函數的模型,如下所示。
目標函數:
(1)
約束條件:
Di,j≤Bi,j+1
(2)
Qu,m,c-Pu,m,c=tu,m,i,j
(3)
Pu,m,c+1≥Qu,m,c
(4)
(5)
(6)
(7)
其中:式(2)表示各工件工序具有先后順序;式(3)表示每個機器正在加工的工序不能被打斷;式(4)表示單個機器加工具有順序性,在同一時刻只能加工一個工件;式(5)表示每個工件只能分配給一個FMU進行加工;式(6)表示各個FMU有能力加工完成任意工件;式(7)表示工件的每個工序只能分配至一個機器上進行加工。
2 模型求解
2.1 整體思想
模型求解的整體思路為將機器選擇和工序選擇作為FJSP嵌套于FMU的選擇問題中。FMU選擇產生的解作為FJSP的輸入,FJSP的輸出作為FMU選擇解的評價指標,用于指導FMU選擇產生更優解。
由于該研究問題屬于NP-hard問題,故選用粒子群算法進行求解。標準粒子群算法收斂速度快,能夠較為容易地得到較優解,但同時存在著早熟收斂的缺陷[7]。為了解決該問題,本文對標準粒子群算法進行改進,提出了基于二階振蕩的隨機權重混合粒子群算法(RWSecVibratPSO),提高算法的全局搜索能力,算法流程圖如圖2所示。

圖2 RWSecVibratPSO流程圖
2.2 算法具體設計
算法分為FMU選擇和FJSP兩部分。FMU選擇嵌套FJSP。二者均采用RWSecVibratPSO算法進行求解。
a)FMU選擇
1)粒子編碼
本文設計FMU選擇的每個粒子表示的信息為各個待加工工件分配至各個FMU的概率,概率變化范圍為(0,1)。
2)粒子初始化
假設單個粒子的維度為D1,則每個粒子的速度和位置可分別表示為vi=(vi1,vi2,…,viD1)和xi=(xi1,xi2,…,xiD1)。隨機初始化各粒子的速度和位置,并將各粒子的位置進行轉化,得到各個FMU的分配方案。
本文選擇FJSP作為FMU選擇的適應度函數。FJSP的輸入為粒子產生的各個FMU的分配方案,輸出為FJSP的最小化、最大完工時間。考慮到各個FMU與倉庫中心的距離不同,故根據距離設計影響系數τu,將各個FMU的最小化、最大完工時間乘以τu得到的結果作為單個FMU的最小化、最大完工時間。比較各個FMU的最小化、最大完工時間,取最大值作為該粒子的適應度,并初始化局部最優適應度與全局最優適應度。
3)粒子更新策略
針對早熟收斂的問題,本文提出了改進的混合粒子群算法RWSecVibratPSO,利用二階振蕩提高全局搜索能力,同時引入隨機權重,平衡全局和局部搜索能力。該算法的速度與位置更新方程如下:
vij(t+1)=ωvij(t)+c1r1[pij(t)-(1+ξ1)xij(t)+ξ1xij(t-1)]+
c2r2[pgd-(1+ξ2)xij(t)+ξ2xij(t-1)]
(8)
xij(t+1)=xij(t)+vij(t+1)
(9)
ω=μ+σ×N(0,1)
(10)
μ=μmin+(μmax-μmin)×rand(0,1)
(11)
在前二分之一迭代次數中,取
(12)
在后二分之一迭代次數中,取
(13)
式中:ω為隨機權重;c1與c2為學習因子;r1、r2和rand(0,1)為0~1的隨機數;ξ1和ξ2為隨機數,表示二階振蕩的搜索能力,前期利用式(12)提高全局搜索能力,后期利用式(13)提高局部搜索能力;pij為粒子i的局部最優適應度;pgd為粒子群的全局最優適應度;μ、μmax和μmin分別為隨機權重平均值、最大值和最小值;σ為隨機權重方差;N(0,1)為符合正態分布的隨機數。
b)FJSP
1)粒子編碼
本文FJSP的粒子表示工件在加工序列中下一個被加工的概率。通過對概率排序,根據工件的工藝規程得到相應的加工序列。
2)粒子初始化
隨機初始化粒子的速度與位置,經排序后得到加工序列,作為適應度函數的輸入。
FJSP適應度函數的核心是利用加工序列將加工任務分配至空閑的加工機器。分配的原則為保證當前工序結束時間盡可能早。
根據FJSP的適應度函數,可得到輸入加工序列的機器加工方案,從而確定最大完工時間的適應度。根據初始化粒子的加工序列,可對其適應度進行初始化,進而對局部最優適應度與全局最優適應度完成初始化。
3 仿真驗證與分析
為了驗證RWSecVibratPSO算法的有效性,本文設計了相關的仿真實驗,利用該算法對DMPPSP進行求解,同時選擇標準粒子群算法作為對比算法進行比較分析。
3.1 仿真實驗設計
設定共有3個分布式工廠,其與倉庫中心的距離的比值分別為130、110、100,包含的FMU分別為FMU1、FMU2和FMU3、FMU4。每個FMU包含多個加工機器,其中FMU1與FMU2均包含3臺車床、2臺銑床、2臺磨床與2臺鏜床,FMU3與FMU4均包含2臺車床、2臺銑床、2臺磨床與2臺鏜床。待加工工件共6種,每種工件的加工工序及加工時間如表2所示。現需要加工工件集合A={4,4,4,4,4,4},其中各個數字表示從左到右的序號為工件類型的加工數量。各種類型工件的加工信息如表2所示。

表2 各種類型工件的加工信息
RWSecVibratPSO算法的參數設置分為FMU選擇和FJSP。對于FMU選擇,設定粒子個數為30,迭代次數為50。c1和c2分別取0.5和1.5。對于FJSP,設定粒子個數為50,迭代次數為50。c1和c2分別取2和2.1。隨機權重的取值兩部分相同,即ωmax、ωmin和σ分別取值為0.95、0.75和0.5。
由于各個FMU與倉庫中心的距離不同,故根據距離的比值設計τ1、τ2、τ3、τ4分別為1.3、1.1、1.1、1。
3.2 仿真結果分析
利用RWSecVibratPSO算法求解,得到一個較優解,即將A分解成4部分,分別為{1,2,1,0,0,2}、{2,1,1,2,1,0}、{0,1,1,2,1,0}和{1,0,1,0,2,2},并將其對應分配至FMU1、FMU2、FMU3和FMU4。其最小化、最大完工時間為63.25。各個FMU調度安排的甘特圖如圖3所示。其中縱軸為各FMU的機器編號,橫軸為加工時間,不同顏色區塊對應不同的加工工件,區塊上的編號與6的余數代表其對應的工件類型,當余數為0時代表第6種工件(本刊為黑白印刷,如有疑問可咨詢作者)。

圖3 各FMU調度的甘特圖
為驗證本文算法的優越性,本文采用標準粒子群算法作為對比算法,與RWSecVibratPSO算法在粒子數為30、迭代次數為50的條件下,各獨立運行10次,比較兩種算法得到最小化、最大完工時間的最大值、最小值和平均值,如表3所示。

表3 RWSecVibratPSO與PSO結果對比表 單位:h
由表3可知,本文提出的算法相比于PSO算法具有較強的魯棒性和搜索性,在處理DMPPSP問題方面能力更優。
4 結語
本文針對DMPPSP,將其轉化為DFJSP,提出了基于二階振蕩的隨機權重混合粒子群算法。首先明確了要研究的問題,構建了DFJSP的數學模型;其次確定了算法的整體框架,將FJSP嵌套于FMU選擇中進行求解;再者,設計了基于二階振蕩的隨機權重混合粒子群算法,采用隨機權重平衡全局和局部搜索能力,利用學習因子的二階振蕩提高全局搜索能力;最后,通過實例仿真,驗證了本文算法的有效性和優越性。

