外骨骼上肢康復機器人滑模控制策略研究

管瑞欣

(陜西鐵路工程職業(yè)技術學院，陜西 渭南714000)

0 引言

目前，社會人口老齡化嚴重，且由于一些自然和非自然事件的發(fā)生，例如：交通事故、地震和工作中操作機械失誤等均會造成人類肢體不同程度的運動障礙[1-2]。因此，目前社會需要大量的康復醫(yī)療設備。

康復設備不但減輕了康復醫(yī)療師的工作壓力，而且工作效率高。康復醫(yī)療師采用人工康復訓練均是通過經(jīng)驗來施加作用力的，但是康復設備不但可以解放康復醫(yī)療師，而且可以高精度地完成康復訓練的任務。

目前，研究較多的康復設備主要包含兩個類型：一是繩索驅動康復設備；另一個是外骨骼型的康復設備。由于繩索驅動康復設備工作空間有限，運動精度高，而且重構能力很好，因此，繩索驅動康復設備也吸引了很多學者的興趣：合肥工業(yè)大學訾斌團隊設計了繩索驅動并聯(lián)機器人，主要應用于3D打印和腰部的康復訓練；還針對系統(tǒng)剛度分布和控制策略等進行了研究，并通過實驗測試進行了驗證[2-3]。哈爾濱工程大學張立勛教授、王克義教授和王硯麟博士等對繩索驅動康復機器人的控制策略和系統(tǒng)的運動穩(wěn)定性等問題進行了研究，分別針對平面構型和空間構型進行了研究[4-8]。

但是，繩索驅動康復機器人中繩索只能提供單方向的張力，繩索的柔性會降低系統(tǒng)的剛度，對繩索驅動康復機器人的控制并實現(xiàn)患者安全性具有很大的挑戰(zhàn)。而骨骼型的康復及機器人不存在這個問題，因其具有人機交互契合度高、運動舒適性和靈活性好的性能特點，使得外骨骼型的機器人在工業(yè)、康復和軍事領域均具有很好的應用前景[9-11]。

廣西科技大學高學山團隊研究了一款兩自由度下肢康復機器人，結合模糊PID和傳統(tǒng)PID控制方法進行研究[12]，并進行了實驗分析。汪浩然使用不完全微分PID算法設計了一種雙閉環(huán)控制器，內環(huán)采用PI算法進行速度控制，外環(huán)采用PD算法進行機器人的位置控制[13]。

南京航空航天大學吳青聰團隊研究了一款軟質康復外骨骼機器人，在關節(jié)處引入了柔性驅動環(huán)節(jié)，并設計了模糊神經(jīng)網(wǎng)絡阻抗控制算法，通過定阻抗和變阻抗的實驗研究[14]，變頻率復制訓練時關節(jié)轉矩提升88.3%和57.6%，可以很好地改善康復機器人的穩(wěn)定性。

本文介紹了一種外骨骼上肢康復機器人，在運動學和動力學的基礎上，設計了一種基于名義模型的滑模控制器，并通過實例仿真進行了控制效果的驗證。結果表明控制效果可以滿足上肢康復訓練的基本要求。

1 外骨骼上肢康復機器人運動學

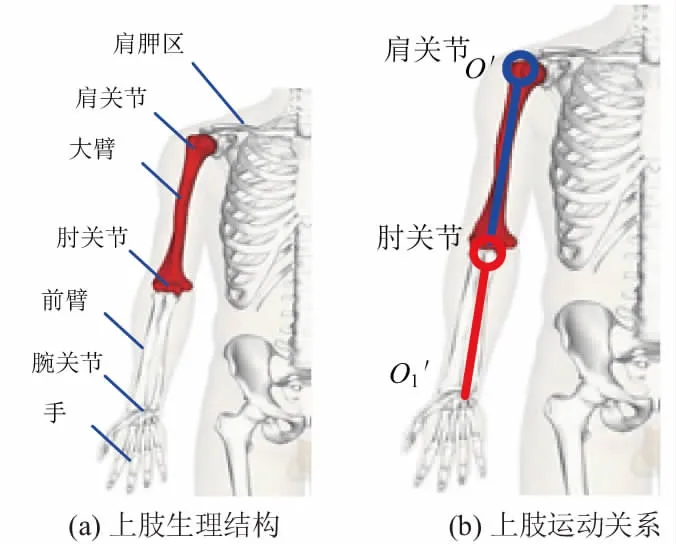
圖1 上肢結構、運動關系和外骨骼機器人構型

如圖1所示，在肩關節(jié)處建立坐標系O-xy，其中：q1和q2分別表示肩關節(jié)和肘關節(jié)的角位移；O1表示外骨骼上肢康復機器人末端在工作空間中的位置(即腕關節(jié)的位置)；m1和m2分別表示外骨骼上肢康復機器人大臂和小臂的質量。上肢大臂和小臂的運動由外骨骼上肢康復機器人的肩關節(jié)和肘關節(jié)處的電機驅動，實現(xiàn)康復機器人的大、小臂的運動。

由圖1可知，外骨骼上肢康復機器人末端在工作空間中的位置O1可以表示為

(1)

則以下關系式可以得到

(2)

從而可以得到

(3)

由圖1可以得到

(4)

根據(jù)余弦定理，由圖1可知

(5)

進一步得到

(6)

假設x=[x1,y1]，q=[q1,q2]，則存在以下關系式：

(7)

式中J為外骨骼上肢康復機器人雅克比矩陣，可以表示為

(8)

通過計算可得：

因此，外骨骼上肢康復機器人雅克比矩陣和機器人結構有關。

2 動力學分析

為實現(xiàn)外骨骼上肢康復機器人的運動控制，需要進一步將關節(jié)角的動力學方程轉化為關于機器人末端位置的動力學方程。

根據(jù)虛功原理[10]可知，在靜態(tài)平衡狀態(tài)下，外骨骼上肢康復機器人末端的作用力Fx和關節(jié)力矩τ之間存在如下關系：

Fx=J-Tτ

(9)

由方程式(7)，可得

(10)

因此，

(11)

一般關節(jié)型剛性機器人的動力學模型可以寫為

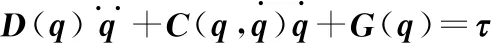
(12)

將式(9)-式(11)代入方程式(12)，并進一步整理可得外骨骼上肢康復機器人的動力學模型：

(13)

其中

3 滑模控制器設計

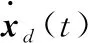
(14)

設計的滑模面函數(shù)為

(15)

則滑模控制器設計為

(16)

式中K>0，為增益矩陣。

將控制律式(16)代入外骨骼上肢康復機器人的動力學模型式(13)，可以得到

Gx(q)+Ks

(17)

(18)

此外，由于Dx(q)是對稱且正定的，因此，定義Lyapunov函數(shù)為

(19)

則有

(20)

(21)

將式(21)代入式(20)并進行整理，得到

(22)

則

(23)

式中：λmin和λxmax分別表示K的最小特征值和Dx(q)的最大特征值，且λ>0，則方程式(23)的解為

V(t)≤e-2λ(t-t0)V(t0)=e-2λ(t-t0)V(t0)

(24)

4 實例仿真分析

分析控制策略的可行性，在MATLAB/Simulink中搭建上肢康復機器人的控制仿真實驗模型，并通過以下具體實例進行分析。上肢康復機器人具體結構參數(shù)如下：l1=l2=0.5m，外骨骼上肢康復機器人的大、小臂質量分別為m1=1.24kg和m2=0.92kg，末端的負重為0.5kg；重力加速度g=9.8m/s2。

假設上肢康復機器人末端的運動期望軌跡為

(25)

外骨骼上肢康復機器人的控制結構如圖2(a)所示，其中控制器采用式(16)所示的滑模控制律，通過檢測外骨骼下肢康復的運動狀態(tài)并進行反饋，和運動期望進行比較，得到實際跟蹤軌跡的運動誤差作為滑模控制器的輸入，最后由控制器控制外骨骼上肢康復機器人的運動，進而實現(xiàn)閉環(huán)控制。

在MATLAB/Simulink中搭建上肢康復機器人的控制仿真實驗模型如圖2(b)所示，其中Sliding_model_ctrl模塊和Robot_model模塊分別表示通過S-Function編寫的滑模控制算法模型和上肢康復機器人模型，Desired_trajectory表示給定的運動期望，如式(25)所示。

圖2 控制結構框圖和仿真實驗模型

通過設置仿真模型的結構參數(shù)和控制器參數(shù)，對上肢康復機器人滑模控制器的軌跡跟蹤性能進行實驗驗證。在上述滑模控制器的作用下，外骨骼上肢康復機器人的運動狀態(tài)如圖3-圖6所示。圖3為外骨骼上肢康復機器人的末端位置變化曲線，由于機器人末端的初始位置為(1,1)m，而期望軌跡的初始位置為(1,1)m，位置誤差導致在機器人初始的運動誤差較大，特別是y1的誤差更為明顯，但是大約在0.38s處機器人可以很好地跟蹤期望的運動。

圖3 末端位置跟蹤曲線

圖4為外骨骼上肢康復機器人末端運動速度變化曲線。同樣，由于實際初始位置和期望運動的初始位置的差別，導致機器人末端的運動速度在開始運動時誤差較大，但大約在0.38s以后，機器人末端的運動速度可以很好地跟蹤期望的運動。

圖4 末端速度跟蹤曲線

圖5為康復機器人大、小臂末端作用力Fx和關節(jié)驅動力矩τ的變化曲線，肩關節(jié)的驅動力矩在開始運動時存在較大的抖動，而且康復機器人小臂末端輸出的作用力也在開始運動時存在較大的抖動，這也是由于實際初始位置和期望運動的初始位置的差別所導致的。大約在0.38s以后關節(jié)力矩和大、小臂末端的輸出力變化是平緩的。

圖5 Fx和τ變化曲線

圖6為上肢康復機器人末端的運動軌跡跟蹤曲線，圖7為康復機器人末端的運動誤差。由圖可知，在初始運動時，由于y方向的初始位置和期望位置相差較大，因此運動誤差較大，但在0.32s以后，康復機器人末端的實際運動可以很好地跟蹤期望的運動。綜上所述，設計的滑模控制器對康復機器人的運動具有好的運動控制效果，可以滿足上肢康復訓練的基本需求。

圖6 運動軌跡跟蹤效果

圖7 運動誤差

5 結語

針對外骨骼上肢康復訓練的需求，介紹了一款兩自由度外骨骼上肢康復機器人。為了實現(xiàn)對外骨骼上肢康復機器人的實時控制，在機器人的運動學和動力學的基礎上，設計了滑模控制器對康復機器人進行控制。通過仿真實驗驗證了所設計的控制器對康復機器人的運動具有較好的控制效果，可以滿足上肢康復訓練的要求。