基于電力大數據的中國工業增加值現時預測

彭放，彭高群，祁亞茹，劉甜甜，周曉磊

（1. 國家電網有限公司大數據中心，北京 100031；2. 清華大學社會科學學院，北京 100084）

1 引言

作為國民經濟的“晴雨表”，電力數據可以及時、客觀地反映經濟發展的真實情況。伴隨著電力信息化的發展，如何充分挖掘電力數據的價值服務于經濟社會發展、政府政策制定成為關注的重點。工業增加值是衡量實體經濟運行狀況的重要指標，對其進行更加及時、準確地預測有助于政府更快、更準確地了解經濟形勢，為經濟政策制定提供可靠的依據，同時也將有助于企業和個人準確把握經濟形勢并進行決策。在當前經濟下行壓力增加、不確定性加劇的環境下，及時準確地預測工業增加值顯得尤為重要。為此，本文以工業增加的現時預測為出發點，充分挖掘電力大數據在現時預測中的作用。現時預測最初被用于氣象領域，近年來被引入經濟領域，是對當前經濟形勢的預測，其基本原理為在官方發布相關統計數據之前，充分挖掘先行高頻數據的信息預測當前經濟形勢[1]。

當前關于中國工業増加值預測的研究相對較少，且主要基于所選擇的若干傳統統計指標進行，如利用社會消費品零食總額、廣義貨幣數據對工業增加值進行預測[2]，基于構建的民營企業信用利差指數對工業增加進行預測[3]。在宏觀經濟傳導機制愈發復雜、工業增加值影響因素更加多元的情形下，恰當的預測模型應當包含大量的解釋變量以充分利用有價值的信息，僅利用少數幾個變量較難獲得精準的預測。此外，傳統統計數據發布得滯后致使預測時難以利用經濟活動的當前信息，而電力大數據與經濟活動密切相關且實時可得，可提供經濟活動的當前信息彌補傳統統計數據的不足。因此，綜合利用電力數據和傳統統計數據可能得到更加準確的工業增加值預測結果。然而，這不可避免地引出工業增加值預測中傳統數據和電力數據的關系問題，即工業增加值預測中電力數據是否可以替代傳統數據，較之于成熟的統計數據電力數據的用處不大，兩者是否可以相互補充。該問題同樣也是大數據時代基于新興數據進行宏觀經濟預測時可能碰到的問題，但當前卻鮮有文獻對此進行研究。本文設計了5類模型以探究工業增加值預測中統計數據與電力大數據的關系，同時采用多種預測方法進行預測以期獲得更佳的預測效果。

2 研究設計

2.1 預測模型

為充分探究上述工業增加值現時預測中傳統經濟統計數據和電力數據的關系問題，設計兩類數據結合的5種方式：其一，僅利用傳統統計數據進行預測；其二，以傳統經濟統計數據預測為主，以電力數據預測為輔；其三，僅利用電力數據進行預測；其四，以電力數據預測為主，以統計數據預測為輔；其五，同時無差別地利用經濟統計數據和電力數據進行預測。本文基于這5種結合方式構建了如下5類相應的預測模型。

模型1：

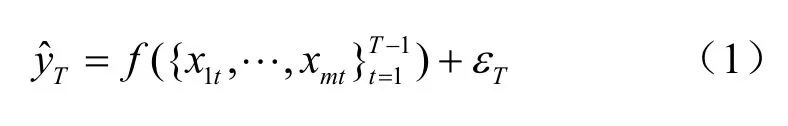
本模型分析僅利用傳統經濟統計數據預測y的預測效果。模型中表示在T期預測時可用的信息集，由于經濟統計數據的發布存在滯后性，所以信息集中僅包含T?1期及其以前的統計數據信息。

模型 2：

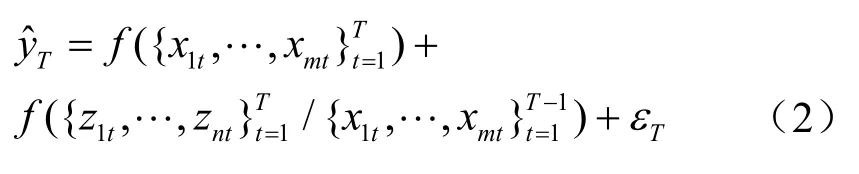
本模型利用傳統經濟統計數據和電力數據預測y，在預測時以統計數據預測為主，以電力數據預測為輔。模型中表示在T期預測時可用的信息集，由于電力數據實時可得，所以預測第T期y值時可用到電力數據的當期值，即第T期的值。表示利用電力數據具有但不包含于統計數據中的信息進行預測。

模型3：

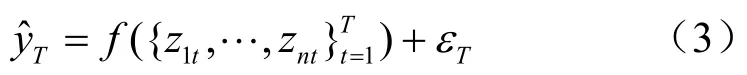
本模型分析僅利用電力數據預測y的預測效果。模型中表示在T期預測時可用的信息集，由于電力數據實時可得所以預測時可用到電力數據的當期值。

模型4：

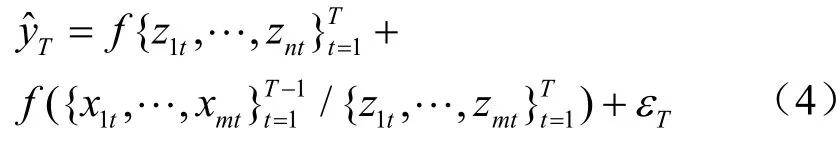
本模型利用傳統經濟統計數據和電力數據預測y，在預測時以電力數據預測為主，以統計數據預測為輔。模型中表示在T期預測時可用的信息集，表示在利用統計數據進行預測前先將統計數據中包含的電力數據信息去除。

模型5：

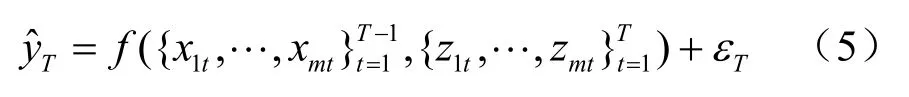
模型5綜合利用傳統統計數據和電力數據預測工業增加值，其與模型2、模型4的區別在于本模型在預測中無差別地對待兩類數據。

2.2 預測方法

面對眾多的解釋變量，如何有效地利用其包含的信息是影響預測結果的關鍵問題。采用參考文獻[4]提出的擴散指數（diffusion index，DI）算法、參考文獻[5]提出的Bagging算法以及參考文獻[6]提出的Boosting算法進行預測。

2.2.1 DI算法

DI算法為數據豐富環境下的常用預測方法，下面對擴散指數方法做簡要介紹。對數據集，首先，基于模型提取的共同因子ft=(f1t,…,fqt)，然后利用提取的因子ft構建如下模型并進行預測：

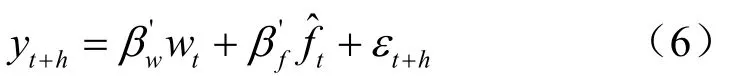
其中，yt為預測目標變量，為估計的因子向量，tw為可觀測向量。對因子個數q的估計可利用如下信息準則[7]：

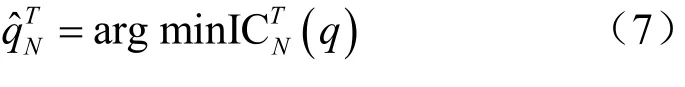
其中：

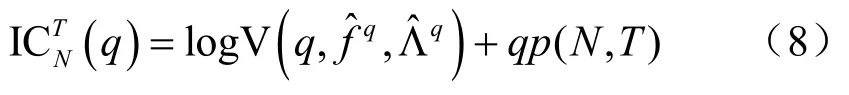
可以看出DI算法分為兩步：首先，從眾多變量構成的信息集中提取因子；然后，將因子納入預測模型進行預測。第一步的因子提取既實現了降維又充分利用了大量變量的信息，但在提取因子時并未考慮信息集中的變量是否有助于預測，這可能導致納入模型的因子不僅無助于預測反而降低了預測精準度。為此，采用Bagging算法[5]、Boosting算法[6]解決上述問題以提高工業增加值的預測精度。

2.2.2 Bagging算法

Bagging為bootstrap aggregation的縮寫，由Breiman提出[8]。該算法基于提取的bootstrap樣本訓練模型并進行預測，上述過程重復若干次后將所有預測值的均值作為最終預測結果。近年來，部分學者將其用于經濟時間序列的預測[9-10]，本文參照參考文獻[5]的做法進行預測，相應Bagging算法可表述為：

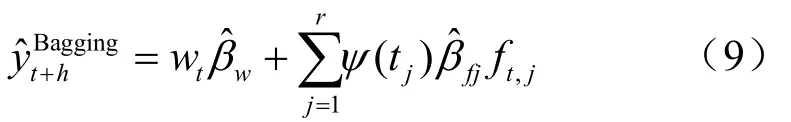
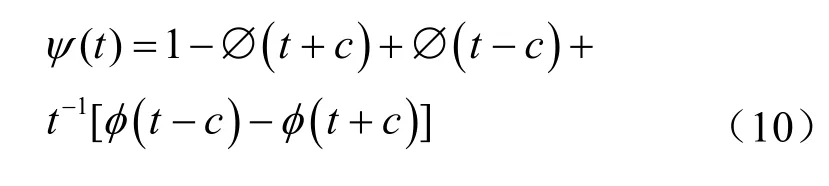
其中，?為標準正態分布函數，φ為標準正態密度函數，c為預先設定的值。

2.2.3 Boosting 算法

Boosting算法是一族可將弱學習器提升為強學習器的算法，一般可表示為如下形式：

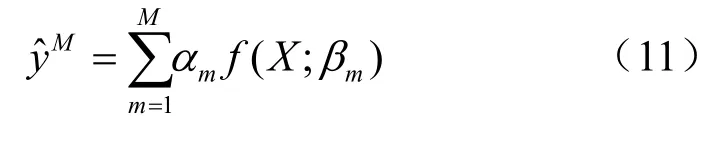
其中，αm為權重，f(X;βm)為定義在信息集X上函數。參考文獻[11]提出的Boosting算法在每次迭代中僅利用一個變量，使得Boosting算法可適用于存在大量變量且數據滿足獨立同分布的場景，參考文獻[6]進一步優化了參考文獻[11]的算法，利用Boosting算法處理時間序列問題。采用參考文獻[6]提出的Component-Wise L2 Boosting算法挑選用于預測的因子，若將Boosting算法作用于因子后得到的值記為，那么最終預測值為：

3 實證分析

3.1 數據說明與處理

本文選擇的數據分為兩類：傳統經濟統計數據和電力數據。所有變量均采用同比增長率，時間跨度為2014年1月至2017年12月。傳統統計數據主要包括居民消費價格指數、名義有效匯率、上證交易所和深證交易所各類指數、商業信心指數、貿易指數、貨幣供應、存款、宏觀經濟景氣指數等42個變量，這些數據來源于CEIC數據庫。電力數據為不同行業購電量數據的同比值，相關數據來源于國家電網大數據中心。

從信息集中提取因子要求信息集中的變量必須為平穩變量，為此本文采用常用的增廣迪基?富勒（augmented Dickey-Fuller，ADF）單位根檢驗方法檢驗變量的平穩性。ADF檢驗通過對如下3個模型的檢驗進行。

其中，Yt表示被檢驗的時間序列，Δ為差分算子，即ΔYt=Yt?Yt?1。上述3個模型的零假設均為H0：δ= 0，即時間序列是不平穩的。上述3個模型只要有一個模型拒絕了零假設就認為時間序列是平穩的，如果3個模型都不能拒絕零假設則認為時間序列非平穩。對于被檢驗變量，若檢驗表明其不平穩，則對其取差分并再次檢驗其平穩性；若變量差分后仍不平穩，則再次進行差分。限于篇幅原因，本文不給出變量平穩性的檢驗結果及對非平穩變量的差分情況。

3.2 基準模型與效果評估

本文選擇自回歸滑動平均（auto-regressive integratedmoving average，ARIMA）模型作為基準模型，采用均方預測誤差（mean squared forecast error，MSFE）測度模型的預測效果，MSFE的計算式如下：

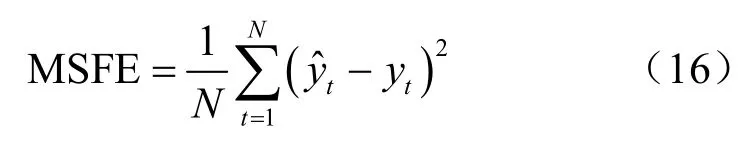
其中，MSFENBM為非基準模型的均方預測誤差，MSFEBM為基準預測模型的均方預測誤差。rMSFE小于1，則說明非基準模型較基準模型有更好的預測效果，而且比值越小說明非基準模型的預測效果越好。

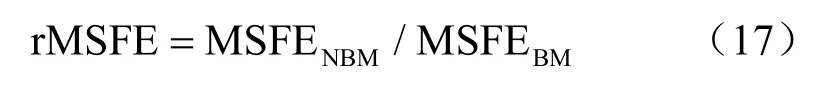
3.3 結果比較與分析

本文在估計模型和進行預測時采用了移動窗口和累積窗口兩種方法。累積窗口法，即在下一期預測時，將前面所有樣本（包括上一期）的真實值作為訓練集放入估計模型中，訓練集逐期增加。移動窗口法，就是固定訓練集觀察值的長度，每往后預測一期，訓練集往后移動一期。本文選擇2014年1月至2017年6月期間的數據作為訓練集，選擇2017年7月至2017年12月期間的數據作為預測集。

為充分探究電力數據在工業增加值預測中的作用，報告基于電力數據指標不同分類與傳統統計數據組合的預測效果進行了分析，表1至表9分別呈現了不同模型與數據組合預測工業增加值的rMSFE。考慮電力數據實時可得的特點，本文采用兩種方式利用電力數據信息：其一，僅利用電力數據當期信息，即表1至表9中數據無滯后；其二，不僅利用電力數據的當期信息還利用其滯后信息，即表1至表9中數據有滯后。

表1呈現了基于居民和企業總用電數據與統計數據現時預測工業增加值的rMSFE，表2呈現了利用全行業用電一級指標數據與統計數據現時預測工業增加值的rMSFE。由表1和表2可以發現以下結論。

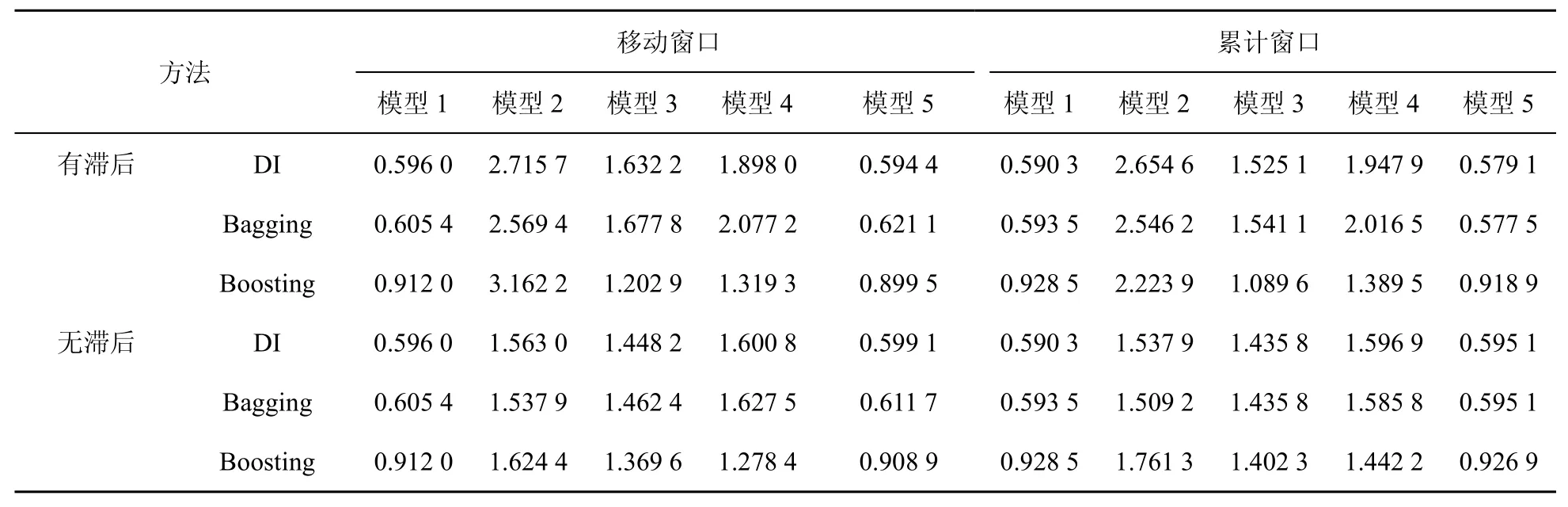
表1 基于居民和企業總用電數據與統計數據預測工業增加的rMSFE

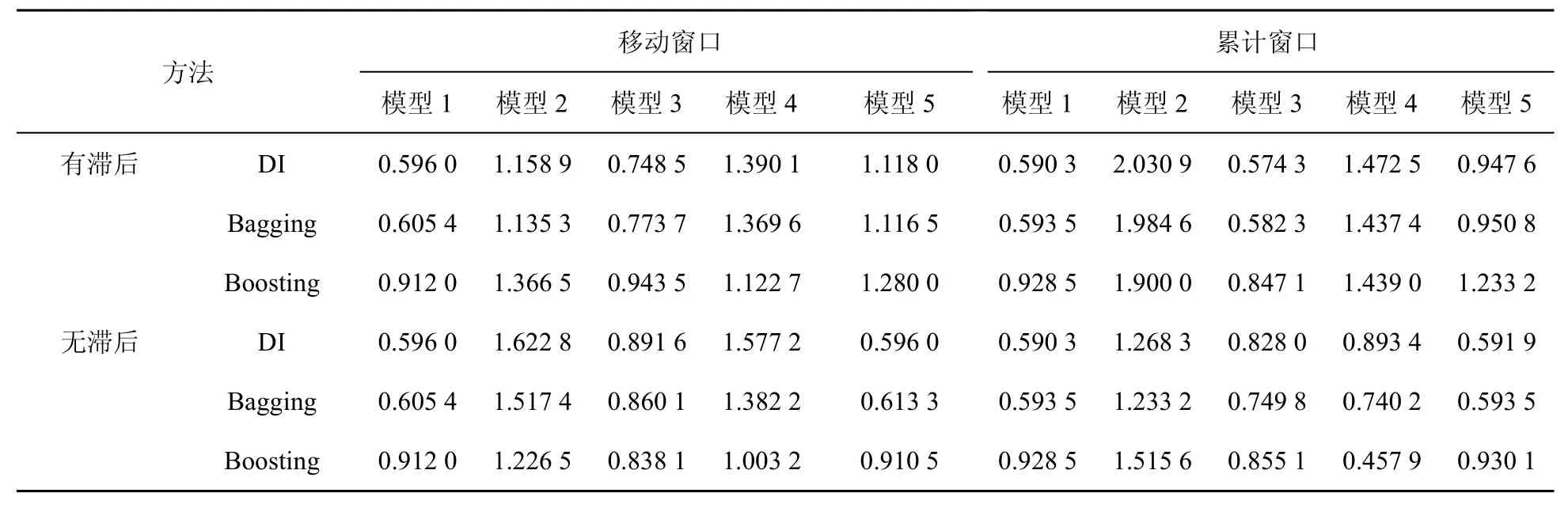
表2 基于全行業用電一級指標數據與統計數據預測工業增加的rMSFE

（1）對模型1，TMSFE均小于1，這意味著利用ARIMA模型的預測結果并不是最優的，基于大量傳統統計數據的預測效果要優于ARIMA模型。

（2）對模型2到模型5，與僅利用電力數據當期信息的預測效果相比，利用電力數據當期和滯后信息的預測效果更好。為此本文僅就存在滯后信息的情況進行分析。

（3）對模型3，其在表2中的預測效果要優于在表1中的預測效果，而且前者的效果要優于ARIMA模型，后者的預測效果與ARIMA模型相比較差。這意味著相對于居民和企業總用電數據，電力全行業一級指標用電數據包含更多有助于工業增加值預測的信息。

（4）對模型2，可以發現利用電力全行業一級指標以及居民和企業總用電量的預測效果均不優于模型1，而且利用電力數據全行業一級指標的預測效果與利用居民和企業總用電量的預測效果相比更優，這意味著居民和企業總用電量包含更多無助于工業增加值預測的信息。

（5）對模型4，可以發現其大多數情況下預測效果比模型3差，這表明在剔除相應電力數據信息后，統計數據剩余信息含有較多無助于工業增加值預測的噪音。對模型5，由于無差別地利用兩類數據，且表1、表2所用電力數據指標個數分別為1和8，基于因子提取的機理可推斷模型5的預測效果在表1中其接近于模型1，在表2中其接近于模型3。

上述分析表明，就工業增加值的預測而言，電力數據全行業一級指標比居民和企業用電總量指標含有更多有用的信息，但仍包含較多無助于預測的信息，為此接下來的分析將減少電力數據指標涉及的行業。表3、表4分別給出了利用第二產業總用電數據與傳統統計數據、工業總用電數據與傳統統計數據現時預測工作增加值的rMSFE。觀察表3、表4可以發現以下結論。

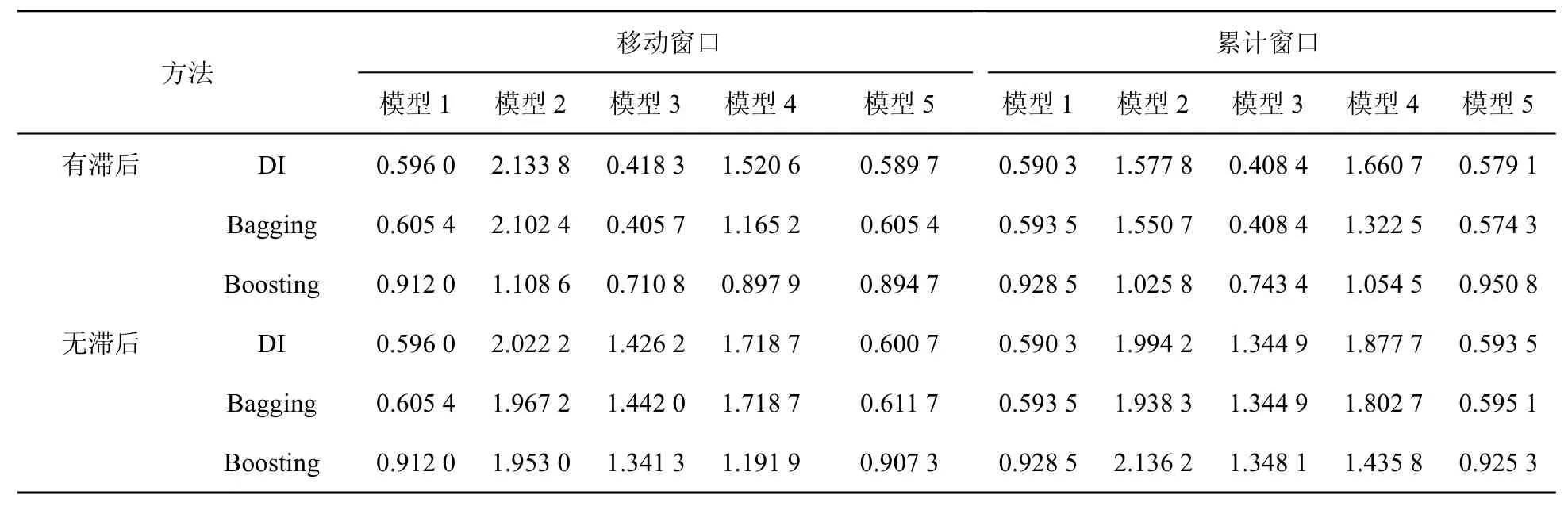
表3 基于第二產業總用電數據與統計數據工業增加的rMSFE

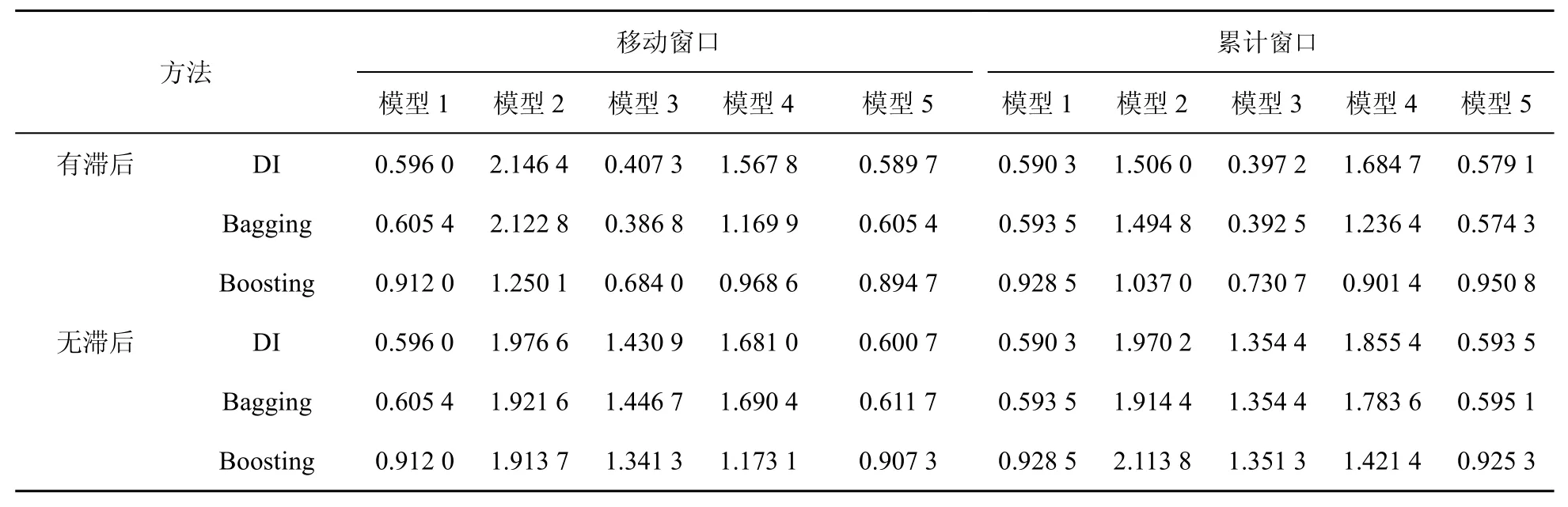
表4 基于工業總用電數據與統計數據工業增加的rMSFE

（1）對模型2到模型5，較之于僅利用電力數據當期信息的預測效果，利用電力數據當期和滯后信息的預測效果更好。這意味著第二產業總用電數據、工業總用電數據的歷史信息較之于當期信息具有更好的預測作用，具有領先性。故下面僅就存在滯后的情況進行分析。

（2）對模型3，在表3、表4中rMSFE均小于1，這表明其預測效果均優于ARIMA模型。此外，由模型3在表4中具有更好的預測效果可知，工業總用電數據比第二產業總用電數據包含更多有助于工業增加值現時預測的信息。

（3）比較模型1和模型3可知，模型3具有更好的預測效果，這表明較之于統計數據，第二產業總用電數據或者工業總用電數據含有更多有助于工業增加值預測的信息。

基于上述分析，工業總用電數據相對于第二產業總用電數據含有更多有助于工業增加值現時預測的信息。考慮工業部門包含不同行業，接下來探究工業部門中不同行業用電數據現時預測工業增加值的能力，預測結果如表5至表9所示。表5、表6分別給出了基于工業部門用電二級指標數據與統計數據、工業部門用電一級指標數據與統計數據的預測效果。觀察表5、表6可以發現以下結論。

（1）對模型2到模型5，用電力當期及滯后期數據的預測效果更好。這同樣表明相關電力數據的歷史信息比當期信息具有更好的預測作用，所以本文僅就存在滯后的情況進行分析。

（2）比較模型3與模型1，顯然前者的預測效果優于后者。這意味著較之于統計數據，表5、表6所用電力數據含有更多有助于工業增加值預測的信息。這點通過比較模型2與模型1、模型4與模型3的預測效果也可以看出。

對比表4、表5、表6中模型3的預測效果可以發現，盡管都利用了工業部門的電力數據信息，但表6中模型3的預測效果卻更好，即利用工業部門用電一級指標數據的預測效果要優于利用工業部門總用電數據及工業部門用電二級指標數據的預測效果。結合因子分析的機理，認為這可能源于工業部門中部分行業的用電數據無助于工業增加預測。故接下來將統計數據分別與表6中所用工業部門用電一級指標（即礦業、制造業、電力、燃氣及水的生產和供應業3個行業各自用電總量數據）結合進行工業增加值現時預測，相應的預測結果見表7、表8、表9。通過比較可以發現以下結論。

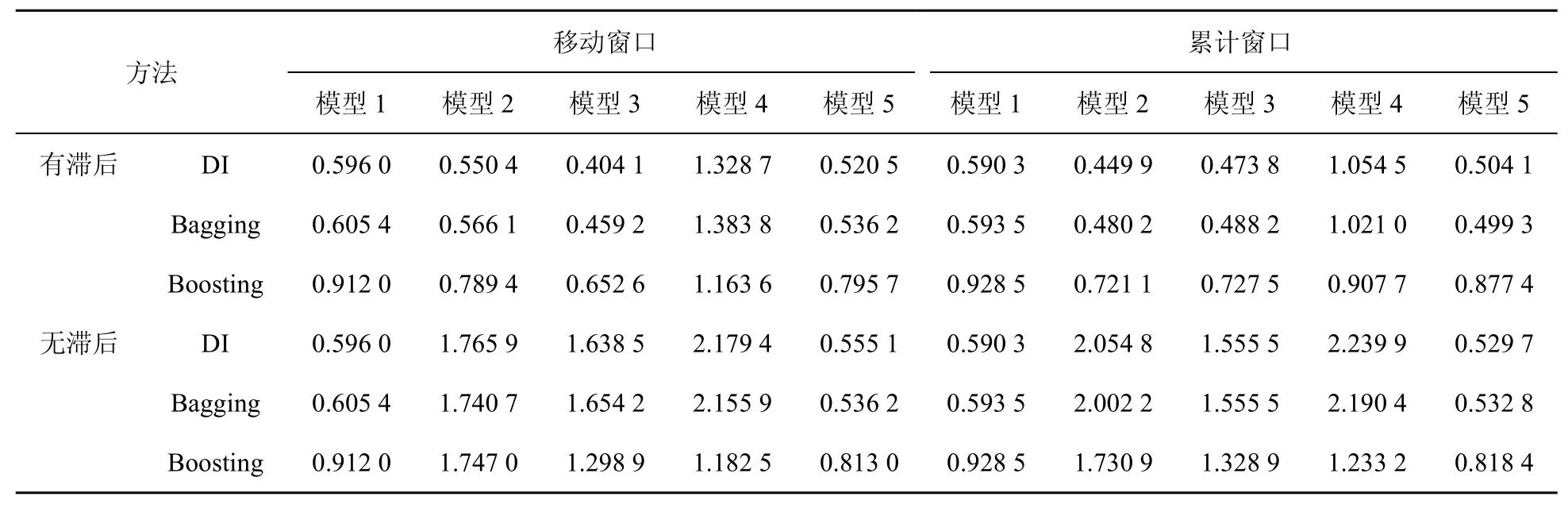
表5 基于工業部門用電二級指標數據與統計數據工業增加的rMSFE

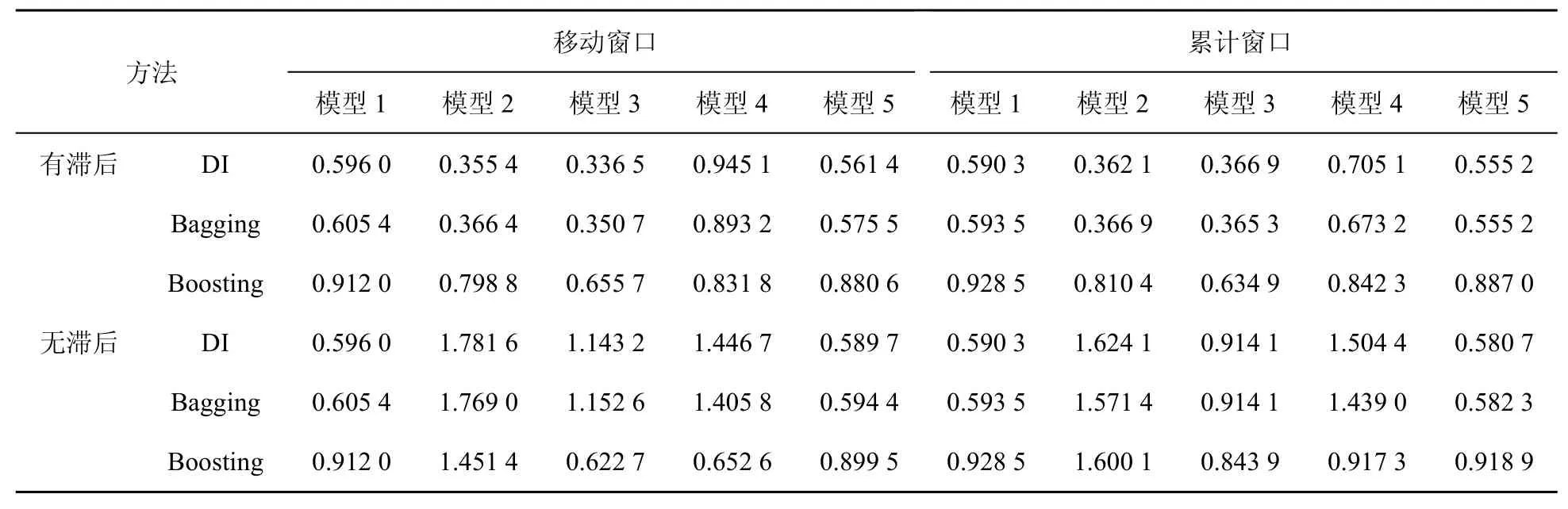
表6 基于工業部門用電一級指標數據與統計數據工業增加的rMSFE

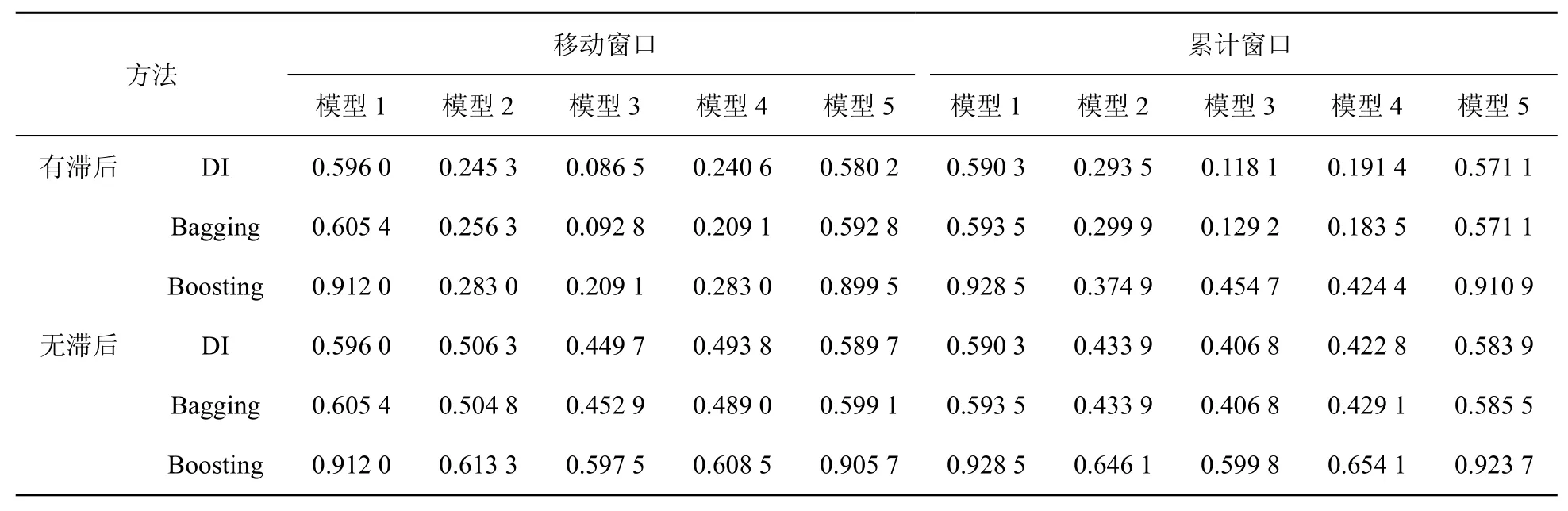
表7 基于采礦業總用電數據與統計數據工業增加的rMSFE

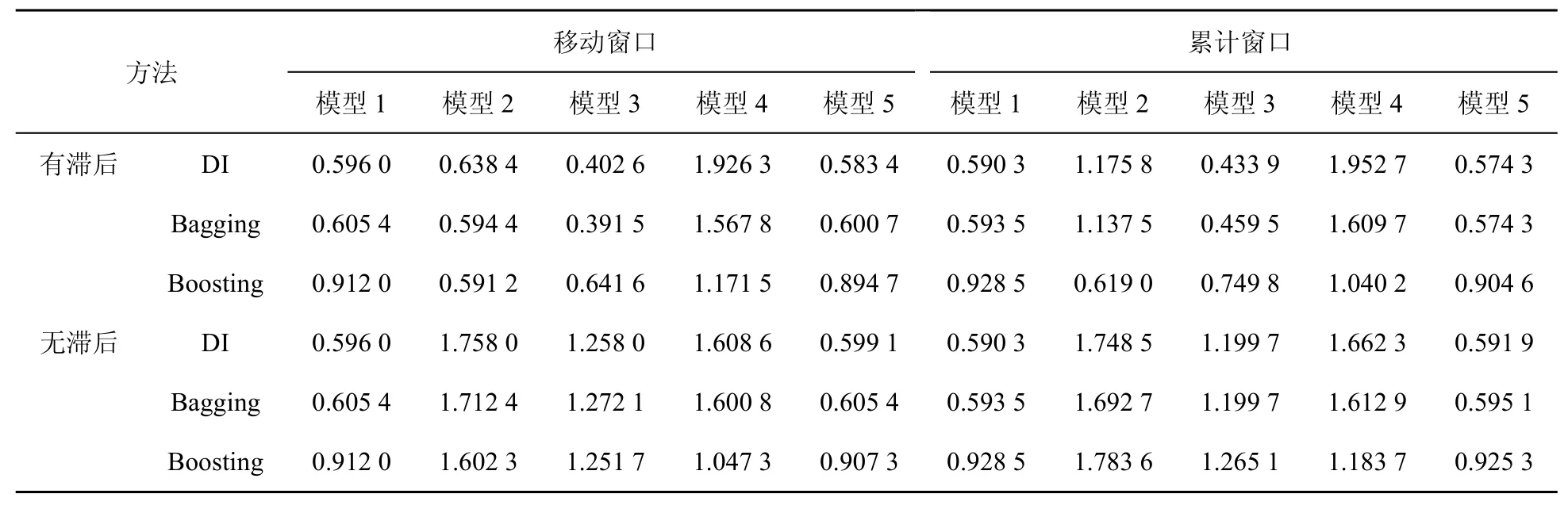
表8 基于制造業總用電數據與統計數據工業增加的rMSFE

表9 基于電力、燃氣及水的生產和供應業總用電數據與統計數據工業增加的rMSFE

（1）對模型2到模型5的預測效果，在表7和表8中利用電力數據當期及滯后期信息的預測效果較之于僅利用電力數據當期信息的預測效果更優，但在表9中則僅利用電力數據當期信息時的預測效果更好。故接下來的分析對表7和表8僅討論利用電力數據當期及滯后信息的情形，對表9僅討論利用電力數據當期信息時的情形。

（2）對模型3，其在表7、表8、表9中的預測效果依次遞減；模型3在表6中的預測效果明顯地弱于其在表7 中的預測效果，但優于其在表8、表9中的預測效果。

（3）對于模型1與模型3，可以發現在表9中前者的預測效果明顯優于后者，而在表6、表7及表8中后者的預測效果優于前者，特別是在表7中更是如此。

上述關于模型3、模型1在表6、表7、表8及表9中預測效果的分析表明利用電力、燃氣及水的生產和供應業電力數據與統計數據的組合可能不是現時預測工業增加值的最佳組合。此外，在表7中模型2的預測效果優于模型1，而在表8中除Boosting算法外模型2的預測效果并不優于模型1，這在一定程度上表明采礦業總體用電數據去除統計數據信息后仍含有較多有助于工業增加值預測的信息，而制造業總體用電數據在去除統計數據信息后所含有助于工業增加值預測的信息相對較少。

以上部分基于表1至表9中的rMSFE分析了DI、Bagging、Boosting算法與兩類數據不同結合方式的預測效果，圖1給出了上述各表中移動窗口下3種算法各自的最佳預測值曲線，以更加直觀地呈現不同預測方法及數據結合方式的預測效果。觀察圖1可以發現，表3、表4、表6、表7中各預測方法的預測值曲線與工業增加值實際值曲線趨勢一致，預測殘差相對較小，而且就預測值曲線趨勢和預測殘差來看，基于DI算法的預測曲線相對更優。

綜合上述分析可以發現，就工業增加值的現時預測而言，第二產業、工業、采礦業、制造業的總體用電數據均有較好的預測效果，而且采礦業總體用電數據與統計數據的組合是相對更優的數據組合。就預測方法而言，DI的預測效果要優于Bagging、Boosting，這或許與所用數據有關。此外，較之于僅僅利用電力數據當期信息，利用電力數據當期及滯后期信息可實現更好的工業增加值現時預測效果。

4 結束語

伴隨著人類社會邁入大數據時代，部分學者嘗試利用新興大數據進行宏觀經濟預測。新興大數據與傳統經濟統計數據各具優劣，但現有的宏觀經濟預測研究或者側重對一類數據的挖掘應用，或者對兩類數據無區別地使用，涉及對這兩類數據關系的探討及區別對待的研究較少。電力數據作為經濟發展的“晴雨表”，與經濟活動密切相關，但鮮有文獻探究電力數據在宏觀經濟預測中的價值。本文提出了電力大數據與經濟統計數據在宏經濟預測中相結合的5種方式，采用DI、Bagging、Boosting等大數據預測算法，對工業增加值這一重要宏觀經濟指標進行了預測，探究了在工業增加值預測中如何有效地利用電力大數據與經濟統計數據兩類信息以獲得更加及時、準確的預測結果。研究結果表明，基于選擇出的恰當電力指標，可以得到更加及時、準確的工業增加值預測結果。本文的研究可為宏觀經濟預測中如何有效利用新興數據和經濟統計數據兩類信息提供有益的借鑒與啟示。