m法和有限元法對橋梁樁基的計算探討

高能祥，方 健

[同濟大學建筑設計院（集團）有限公司，上海市 200092]

0 引言

樁基是指設置在地面以下一定深度的圓柱狀或管狀的基礎構件，是橋梁等其他各種構筑物中最常用的基礎形式。樁基對地質條件廣泛適用，基礎承載力高，不均勻沉降較小；且當地震發生時，樁基整體破壞的概率小，能夠防止構筑物倒塌，減少人員傷亡和財產損失。隨著施工機械化和檢測技術的發展，樁基的施工速度和施工質量得到大幅提升，樁應用愈加廣泛。

在承受水平荷載作用下，樁基的工作原理是樁-土的相互作用問題[1]。此時，樁基依靠樁基周圍土的抗力來承擔其所受的水平荷載。樁基承受水平力作用下，導致樁基發生水平位移，此時樁基壓迫樁周土產生相同方向的變形，迫使樁周土產生反向抵抗力，此反向抗力會阻止樁基位移的繼續發展。

1 m 法計算簡介

樁基在水平力作用下，最常用的計算方法是地基反力系數法。地基反力系數指的是地基反應模量，即土對樁基產生的反向抗力與土的位移的比值。地基反力系數采用的是Winkler 地基模型[2]。它將樁側土離散為一個個相互獨立的彈簧，且彈簧所產生的抗力與其發生的位移成正比例關系。

式中：p 為樁基所承受的單位壓力；Cz為地基反力系數；yz為相應的土體位移。

根據式（1）建立Winkler 彈性地基梁模型如下：

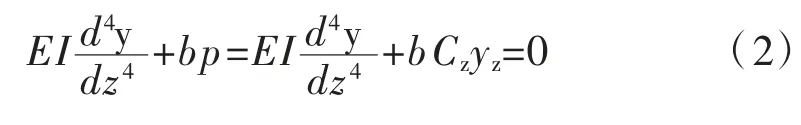
式中：EI 為樁基抗彎剛度；y 為樁基軸線撓曲位移；z為樁基對應深度；b 為樁基計算寬度。

根據地基反力系數Cz沿樁基深度不同的分布圖示，形成了Cz不同的幾種求解方法。

式中：k 比例系數；n 為指數。

如圖1（b）所示，n=0 時，Cz=k，此方法被稱為張（有齡）氏法。該方法認為地基反力系數為常數，不隨樁的深度變化。

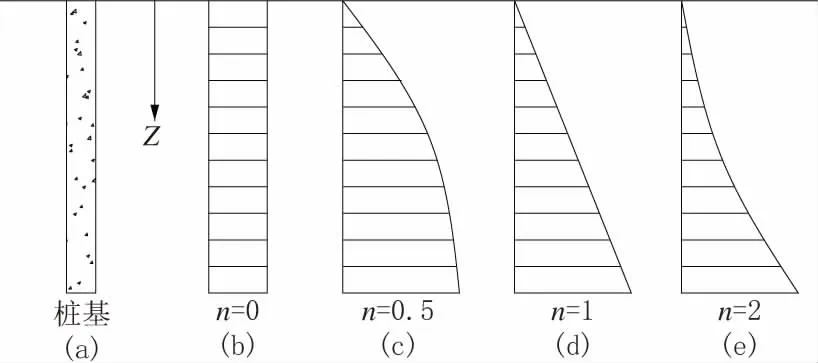
圖1 地基反力系數沿樁基深度的分布圖示

如圖1（c）所示，n=0.5 時，Cz=kz0.5，此方法被稱為C 法。該方法認為地基反力系數沿樁的深度成凸形拋物線變化。

如圖1（d）所示，n=1.0 時，Cz=kz，此方法被稱為m 法。該方法認為地基反力系數沿樁的深度成線性變化，令k=m，則Cz=mz。

如圖1（e）所示，n=2.0 時，Cz=kz2，此方法被稱為k 法。該方法認為地基反力系數沿樁的深度成凹形拋物線變化。此方法由于計算出的樁身彎矩結果比實際偏大較多，故較少采用。

上述中的m 法是我國計算樁基在水平荷載作用下的常用方法，也是《公路橋涵地基與基礎設計規范》（JTG 3363—2019）[3]中計算樁基的水平位移和作用效應的指導方法。根據Cz=mz，重新建立Winkler彈性地基梁模型公式如下：

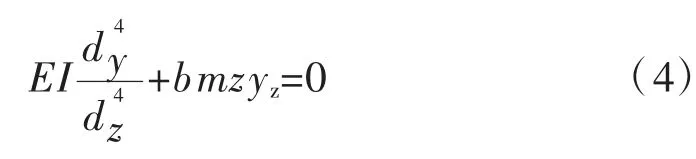
式中：m 為地基反力系數的比例系數；z 為樁基對應深度。

上述公式可寫為：

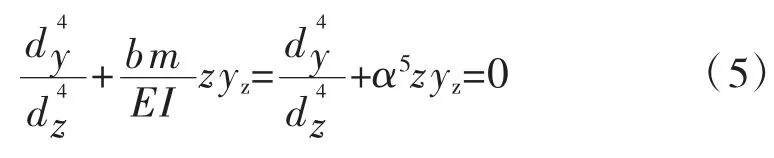
式中：α 為樁基的變形系數，其值為：

當樁基樁頭承受水平推力H0和水平彎矩M0的情況下，根據式（5）可推導出彈性樁的內力和位移公式，如下：

式中：yz為樁的水平變形位移；φz為樁的轉角位移；Mz為樁截面的彎矩；Qz為樁截面的剪力；σz為樁周圍的土壓力；A、B、C、D 為無量綱系數，可通過查詢《公路橋涵地基與基礎設計規范》（JTG 3363—2019）[3]表L.0.8 取用。

2 樁基有限元法模擬簡介

有限元分析是目前結構設計計算的常用方法。它利用結構材料本身的本構關系和結構自身的邊界條件建立結構受力與位移的變形協調方程[4]，求解結構的內力和位移。有限元分析同樣適用于樁基計算分析，采用彈性地基梁理論建立樁基有限元模型，將樁基用梁單元模擬，采用土彈簧模擬土對樁基的約束作用。在樁基的有限元建模中，需遵循如下假設條件：

（1）將土體視為線彈性體，土彈簧剛度隨深度線性增加。

（2）同一深度的彈簧剛度為定值，不隨樁基位移變化[5]。

（3）忽略土體對樁基的摩擦力和黏結力等作用。

根據以上假設，土彈簧剛度計算公式如下：

式中:Kz為深度z 處的土彈簧剛度；b 為樁基計算寬度；m 為地基反力比例系數；hz為深度z 處的土層厚度。

3 算例簡介

本文采用兩個算例進行分析對比，分別為單樁模型和群樁模型。算例簡介如下：

3.1 算例一

算例一為單樁模型，如圖2 所示。采用樁徑為1.0 m 的摩擦鉆孔灌注樁基，樁長20 m。樁端處土性為可塑性黏土，取地基反力系數m=5 000 kN/m4。樁基的計算寬度b 按《公路橋涵地基與基礎設計規范》（JTG 3363—2019）[3]L.0.1 條計算。經計算，b=1.8 m。則由式（12）可計算出樁基各深度處的土彈簧剛度。

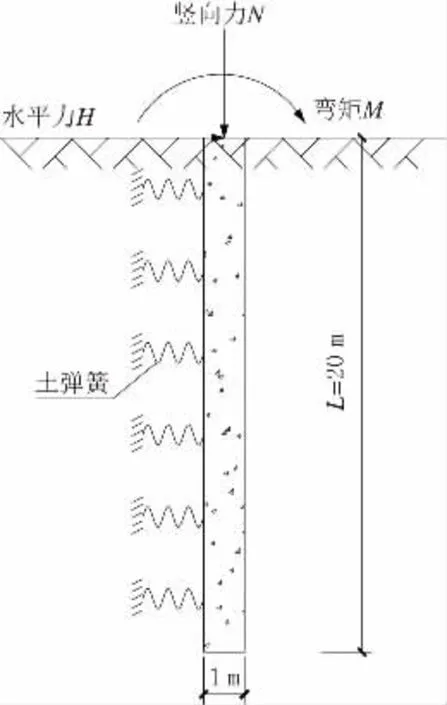
圖2 算例一單樁模型圖示

樁頂施加豎向力N、水平力H 和彎矩M，分別為N=1 000 kN，H=500 kN，M=1 000 kN·m。其中，彎矩與水平力產生的位移效應同向。

3.2 算例二

算例二為群樁模型，如圖3 所示。承臺為2 m高，承臺下設置12 根樁徑為1.2 m 的摩擦鉆孔灌注樁基，樁間距均取3.0 m，樁長20 m。樁端處土性為可塑性黏土，取地基反力系數m=5 000 kN/m4。樁基的計算寬度b 按《公路橋涵地基與基礎設計規范》（JTG 3363—2019）[3]L.0.1 條計算。經計算，b=1.386 m。則由式（12）可計算出樁基各深度處的土彈簧剛度。

圖3 算例二群樁模型樁基平面（單位：cm）

在承臺中心施加豎向力N、水平力H 和彎矩M，分別為N=20 000 kN，H=1 000 kN，M=10 000 kN·m。其中，彎矩與水平力產生的位移效應同向。

4 算例結果對比

采用上節的兩個算例進行分析對比，分別采用m 法和Midas Civil 有限元模型計算樁身的各反應結果，包括樁基水平位移、樁身彎矩、樁身剪力和樁周土應力。

4.1 算例一

單樁模型采用m 法計算的樁身各反應結果見表1。

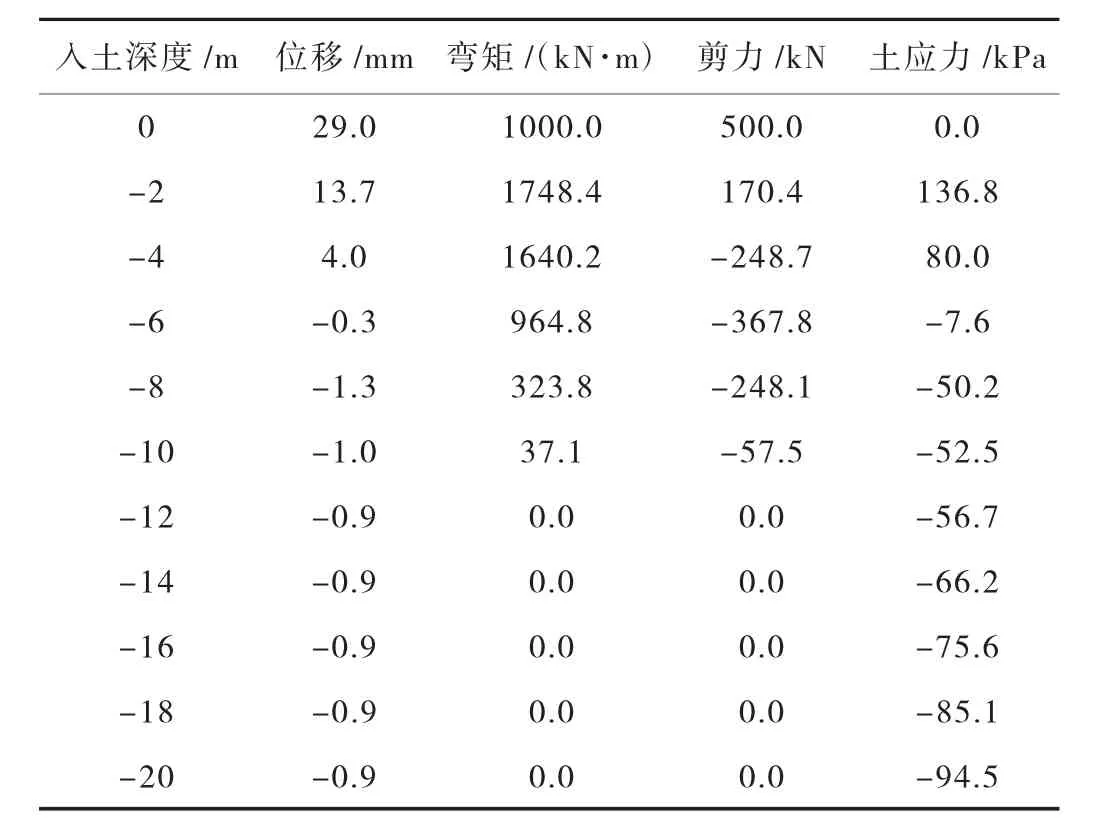
表1 單樁模型m 法計算結果

單樁模型采用有限元法計算的樁身各反應結果見表2。

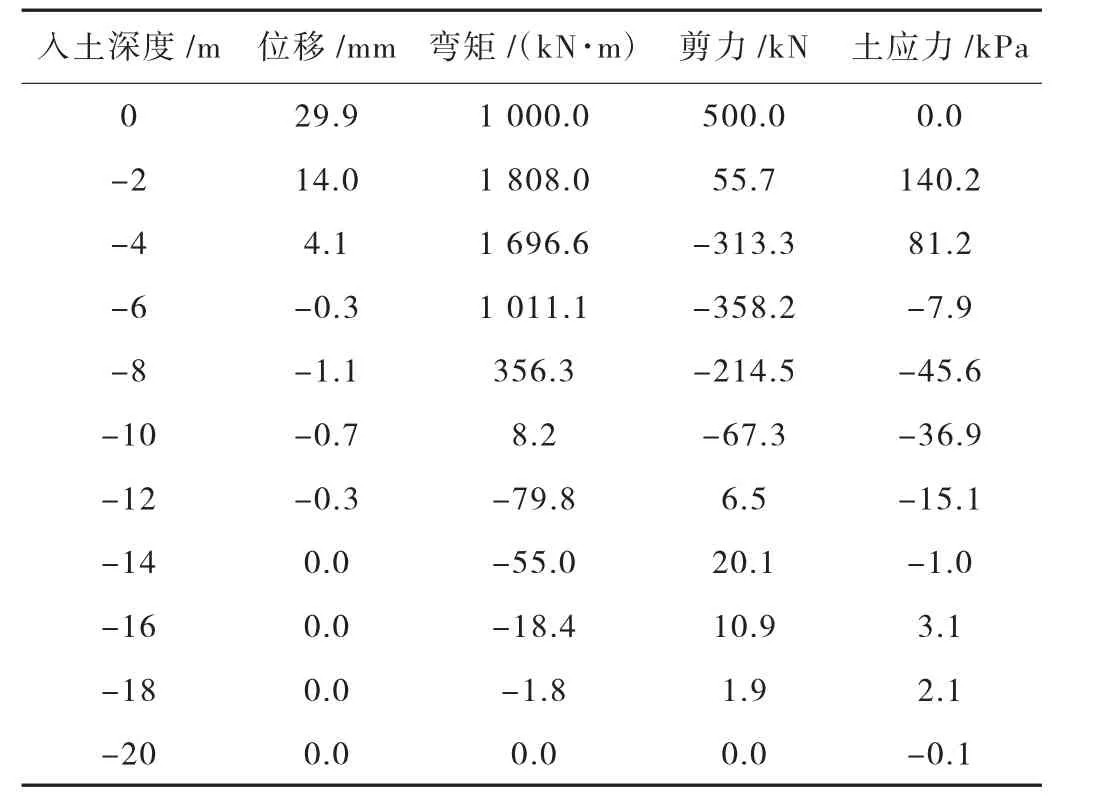
表2 單樁模型有限元法計算結果

單樁模型采用m 法和有限元法計算的樁身各反應結果對比如圖4～圖7 所示，最大值差距見表3。

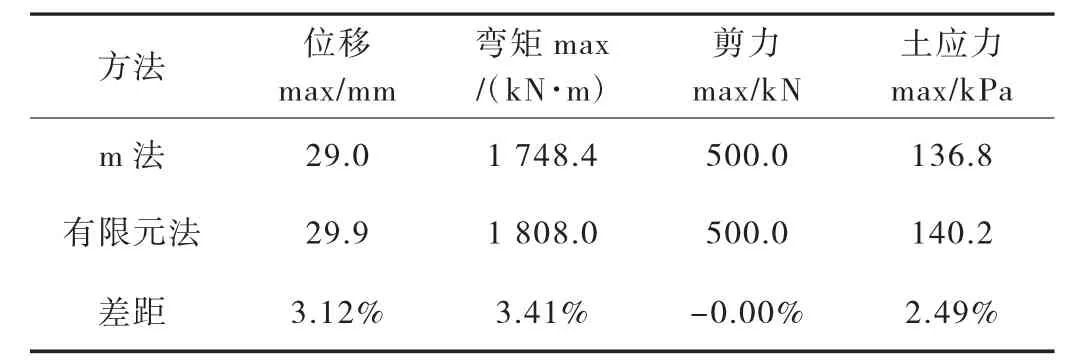
表3 單樁模型樁身結果差距分析

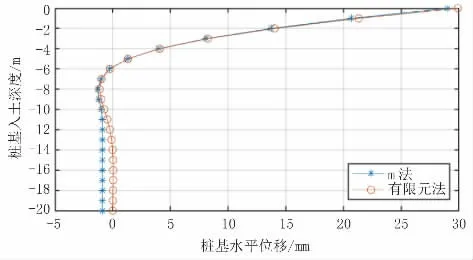
圖4 單樁模型樁基位移結果對比（單位：mm）

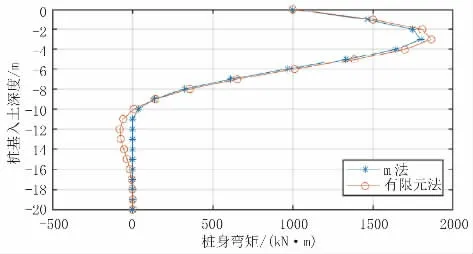
圖5 單樁模型樁身彎矩結果對比（單位：kN·m）

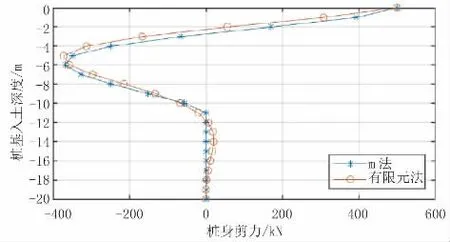
圖6 單樁模型樁身剪力結果對比（單位：kN）

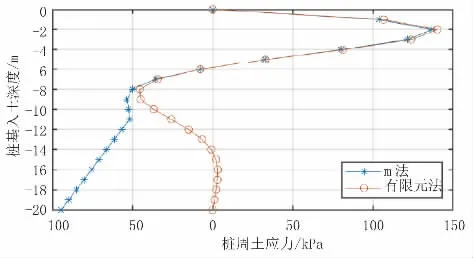
圖7 單樁模型樁周土應力結果對比（單位：kP a）

根據以上計算結果，單樁模型中兩種方法計算出的樁身各反應結果最大值差距均小于5.0%，且除樁周土應力結果外，其他反應結果趨勢較一致。

4.2 算例二

群樁模型采用m 法計算的樁身各反應結果見表4。

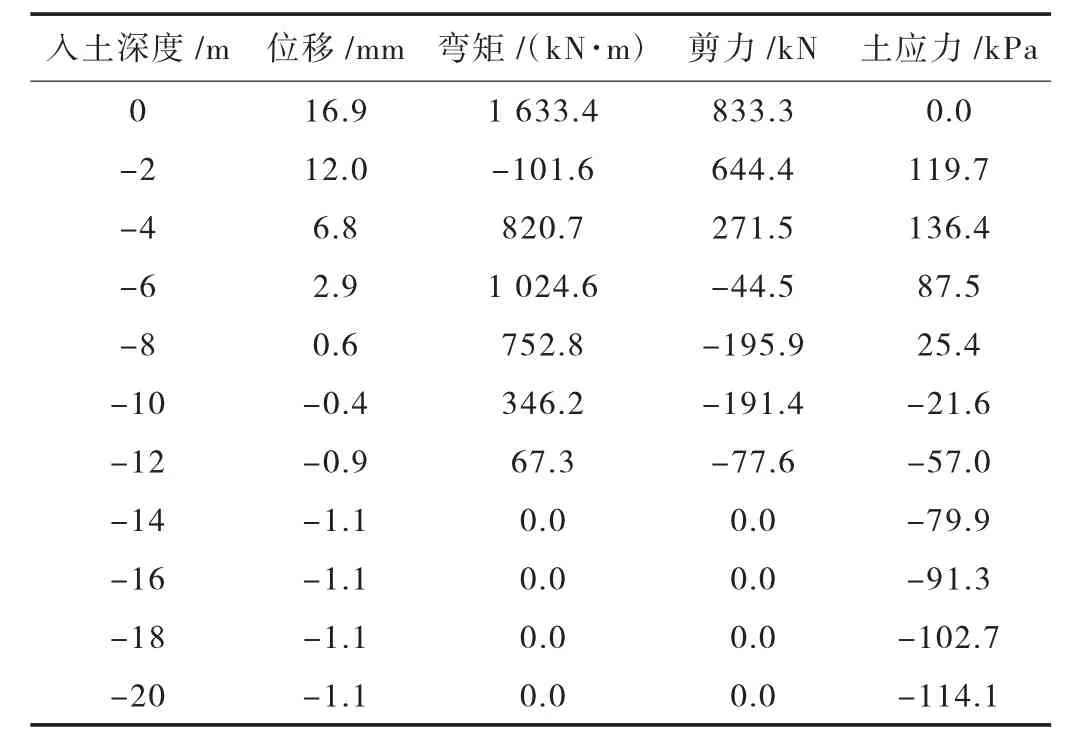
表4 群樁模型m 法計算結果

群樁模型采用有限元法計算的樁身各反應結果見表5。

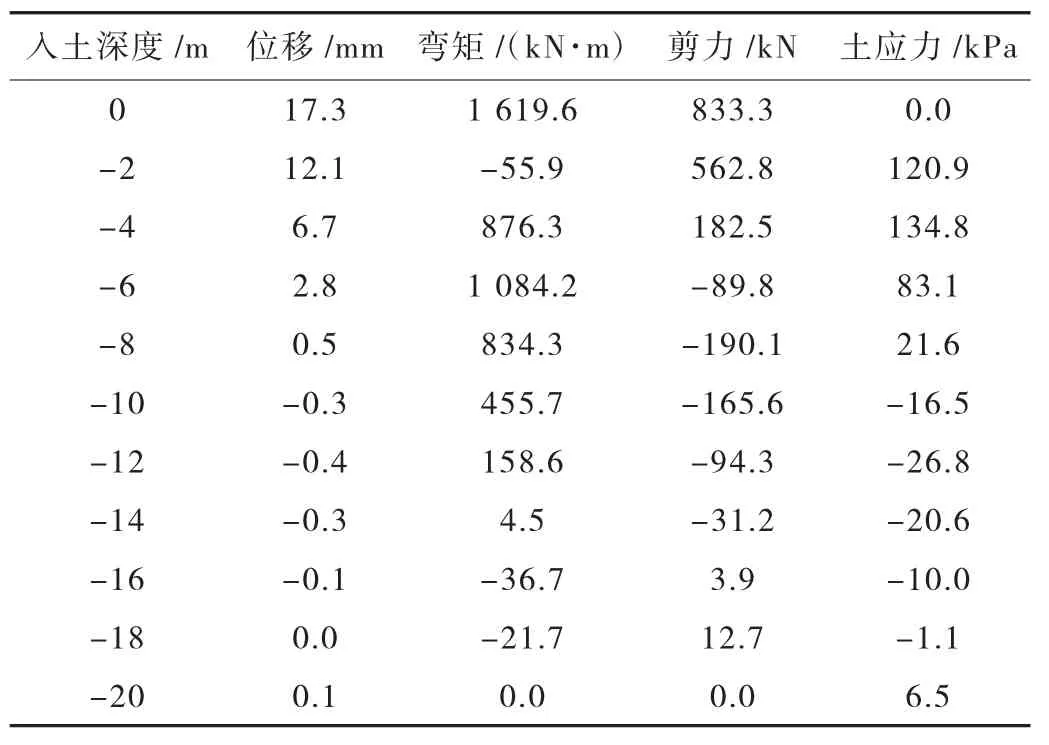
表5 群樁模型有限元法計算結果

群樁模型采用m 法和有限元法計算的樁身各反應結果對比如圖8～圖11 所示，最大值差距見表6。

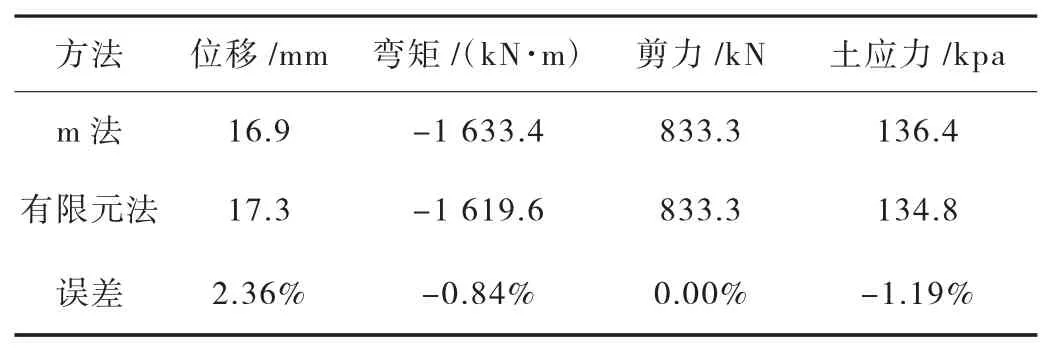
表6 群樁模型樁身結果差距分析

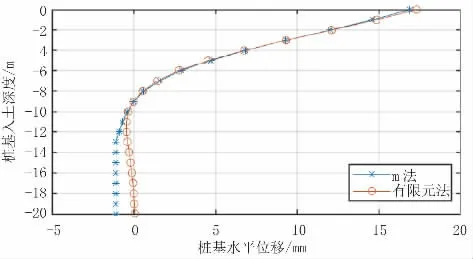
圖8 群樁模型樁基位移結果對比（單位：mm）

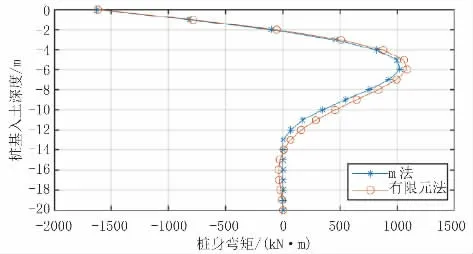
圖9 群樁模型樁身彎矩結果對比（單位：kN·m）

圖10 群樁模型樁身剪力結果對比（單位：kN）

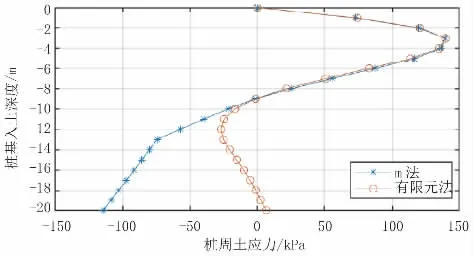
圖11 群樁模型樁周土應力結果對比（單位：kP a）

根據以上計算結果，群樁模型中兩種方法計算出的樁身各反應結果最大值差距均小于3.0%，且除樁周土應力結果外，其他反應結果趨勢較一致。

5 結論

（1）m 法和有限元法在計算的樁身各反應結果差距均較小，且除樁周土應力外，其他反應結果趨勢基本一致，說明兩種方法計算樁身效應均較準確、可靠。

（2）對于樁基水平位移和樁周土應力兩項反應結果，在樁基入土深度較大時，m 法和有限元法計算出的差距較大，且趨勢不太一致。這主要是因為m 法在計算過程中未準確計算深度z≥4.0/α（對于單樁模型z≥10.61 m，群樁模型z≥12.94 m）的樁基位移，導致樁基位移計算結果失真；由于樁周土應力σz=mzyz，進而m 法樁周土應力計算結果失真。所以，在樁基深度z≥4.0/α 的樁基位移和樁周土應力計算結果應以有限元法計算為準。

（3）在樁基計算有限元建模過程中，應注意需將樁基梁單元劃分較細，一般樁基梁單元長度應小于等于1.0 m 為宜；否則會因為樁頭彈簧剛度的模擬不準確導致計算結果與m 法相差較大，導致有限元計算結果失真。