基于ANSYS的深基坑承壓水降壓對周邊環境影響分析

徐 進

[上海市政工程設計研究總院（集團）有限公司，上海 200092]

0 引言

隨著城市化進程的推進，大型城市城區的淺層地下空間幾乎已開發殆盡，城市建設中的軌道交通與給排水基礎設施均需要從更深的地下尋求發展空間，故深基坑工程成為城市建設中繞不開的課題。基坑達到一定深度后，承壓水突涌的風險成為不容忽視的問題。以上海地區為例，承壓水層由淺及深分別為⑦、⑨、?、?、?層，顆粒以粉～ 中砂為主。其中⑦、⑨層與目前深基坑工程關系最為密切，也是承壓水降壓的主要對象。此外，⑤層中部分粉土內也具有一定微承壓性。對于較淺較薄的⑤層承壓水層可以通過隔斷的方式解決抗突涌問題，但對于更深的基坑工程，采取更經濟的懸掛式止水帷幕并結合降承壓水的措施是主流的選擇。

采用懸掛式止水帷幕的深基坑，降低坑內承壓水勢必導致坑外承壓水的降低，從而引起坑外承壓水層土體的固結沉降，進而引起地面上的建（構）筑物及管線的沉降。故精確評價基坑工程中降承壓水對周邊環境的影響成為基坑設計施工實踐中的重要課題。

在承壓水降壓的領域，眾多學者與工程技術人員已進行了大量的研究并取得豐富的成果。龔曉南等[1]針對頂板完全隔水的承壓水層，運用完整井理論與Mindlin 解提出了地面沉降公式；常曉等[2]通過解析的方法得出完整井抽水引起地層的二維變形解析解；鄭剛等[3]通過抽水試驗結合有限元模擬，對天津地區降壓水抽水對土體分層沉降的一般規律進行了研究；雷丹[4]基于上海某地鐵車站基坑抽灌試驗建立了三維有限元模型，分析表明，合理地抽灌措施能有效降低基坑降水的工程風險；徐耀德[5]等利用Modflow 軟件模擬預測出基坑降水下的基坑內外地下水變化，定量評估了基坑降水引起的附加地面沉降。

上述研究成果對指導深基坑工程中降水設計有巨大的參考價值，但也存在一定的局限性，如解析公式的適用范圍較窄，通常要求降水井為完整井或基坑形狀為狹長形等。數值計算方法中有一些采用了復雜的流固耦合模型，需要較多的巖土參數及較強的計算機算力，在實際工程中應用的價值有限。有一些采用商業軟件如Modflow 進行模擬計算，但對于因降水引起的土層固結沉降需要數據導出后進行二次處理，一般的處理做法僅僅是按豎向一維分層總和法將降壓等值線替換為地面沉降等值線。上述做法有三處不足，首先，未考慮水平向的土體固結影響；其次，未考慮承壓水層上部土層的擴散影響。按照常規做法處理后，地表沉降的等值線分布即為承壓水降深等值線的豎向投影，且數值上僅考慮承壓水層的固結沉降量，與實際情況有較大出入；最后，在基坑周邊有深基礎的情況下，無法考量其與土體間的相互作用，通常僅將該處的土體沉降粗略地作為基礎的沉降考慮，且無法直接得出基礎的內力響應。

針對上述問題，本文基于溫度場與滲流場（達西定律）之間的相似性，通過ANSYS 通用有限元軟件中的熱分析模塊模擬基坑工程中的承壓水降壓過程，得出承壓水層水頭降深的空間分布。利用軟件自身熱模塊與結構模塊間單元轉化與計算結果繼承的功能，通過基本土力學公式，將承壓水層水頭降深的空間分布轉化為土體的三維初始應變分布，最后經過結構模塊的計算分析，得出土體位移與結構內力結果。

1 計算原理簡介

1.1 基本原理的相似性

地下水在土體中的滲流遵循達西定律：

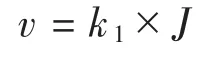
式中：v 為流速，m/s；k1為滲透系數，m/s；J 為水力梯度。

熱傳導遵循傅里葉假定：

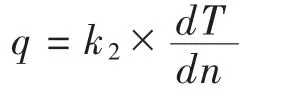
式中：q 為熱流強度，W/m2；k2為熱傳導系數，W/（m·℃）；dT/dn 為溫度梯度，℃/m。

1.2 場方程的相似性

滲流場場方程：

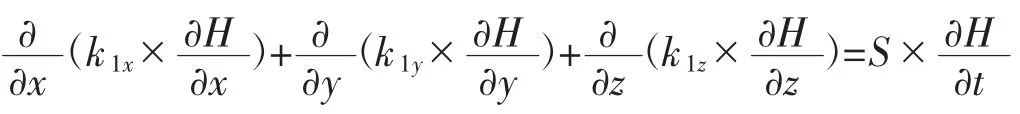
式中：H 為總水頭高度，m；k1x、k1y、k1z為x、y、z 方向上的滲透系數，m/s；S 為土體的貯水系數，1/m。

溫度場場方程：

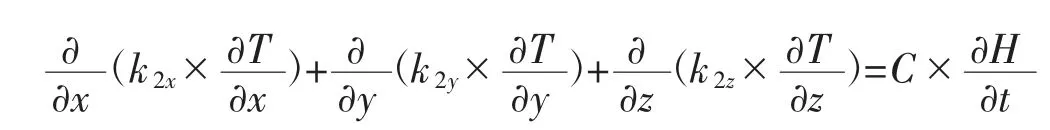
式中：T 為溫度，℃；k2x、k2y、k2z為x、y、z 方向上的熱傳導系數，W/（m·℃）；C 為導熱介質的體積比熱容，J/（m3·℃）。

1.3 初始條件與邊界條件的相似性

滲流場的初始條件即為場內任意一點初始時的水頭高度，可以表達為H=M（x，y，z，t0）。溫度場的初始條件即為場內任意一點初始時的溫度，可以表達為T=N（x，y，z，t0）。

滲流場中的邊界條件有兩類，第一類為水頭隨時間恒定的情況，如承壓水層遠離降水井的水平邊界，可以表達為H=M（x，y，z）；對應溫度場即為溫度隨時間恒定的情況，可以表達為T=N（x，y，z）。第二類為流量隨時間恒定的情況，可以表達為Q1=F（x，y，z），如承壓水層中頂底處不透水層的豎向邊界，對應溫度場即為熱流隨時間恒定（且為0）的情況，可以表達為Q2=G（x，y，z）。

運用Epidata 3.1對數據進行雙錄入，采用SPSS 20.0對數據進行整理與分析。符合正態分布的計量資料以（±s）表示，采用t檢驗進行組間比較；計數資料以例數（%）表示，采用x2檢驗進行組件比較。P＜0.05為差異有統計學意義。

綜上，滲流場與溫度場參數的對應關系可見表1。

表1 地勘土體參數表

2 深基坑承壓水降壓對周邊環境影響分析有限元計算

根據上文分析，ANSYS 10.0 通用有限元軟件中的熱分析模塊可以模擬深基坑承壓水降壓后的水頭分布，此外，此模塊也具備熱應力分析的功能。ANSYS 中的結構模塊可以分析土體與結構的變形與內力。根據ANSYS 軟件的特點，計算分析方案有兩條技術路線可選，第一種是直接耦合法，即進行熱分析的同時進行位移與應力的分析，如ANSYS 中的PLane13、SOLID5 單體等，該單體節點同時具備溫度及位移兩種自由度，這種處理方式適用于兩種分析互為影響的情況；第二種是間接耦合法，即先進行熱分析，將計算結果作為初始條件繼承到結構模塊，同時熱單元轉化為同節點數的結構單元，節點自由度由溫度轉變為位移，進而進行第二次計算分析，最終得到結構計算結果。如SOLID70 熱單元與SOLID45結構單元，這種方法適用于結構計算結果對熱分析影響不大的情況，考慮到基坑降水過程的水頭降深一般小于20 m，即200 kPa 水壓變化，對土體產生的體積應變不大于2%，2%的體積應變對應于土體貯水系數的影響可以忽略不計。我們可以認為基坑承壓水降壓產生的結果影響土體變形有限，而有限的土體變形不會對前者的滲流參數產生反作用。此外，考慮到間接耦合法采用自由度更少的單元，剛度矩陣規模更小，計算中占用的資源更少，故本文擬采用間接耦合法的技術路線。

2.1 背景工程簡介

為了更直觀地描述深基坑承壓水降壓的計算過程，以上海地區某深基坑工程為例進行介紹，基坑工程相關描述如下：

擬建基坑主體結構為污水泵房，開挖面積1 200 m2，平面形狀異形，開挖深度12.6 m～16.8 m，基坑安全等級一級，環境保護等級一級或二級。圍護形式采用1 m 厚地下連續墻+三道鋼筋砼支撐，地連墻以疊合墻的形式兼作主體結構外墻。坑底加固采用高壓旋噴樁裙邊加固。基坑平面布置見圖1，剖面詳見圖2、圖3。

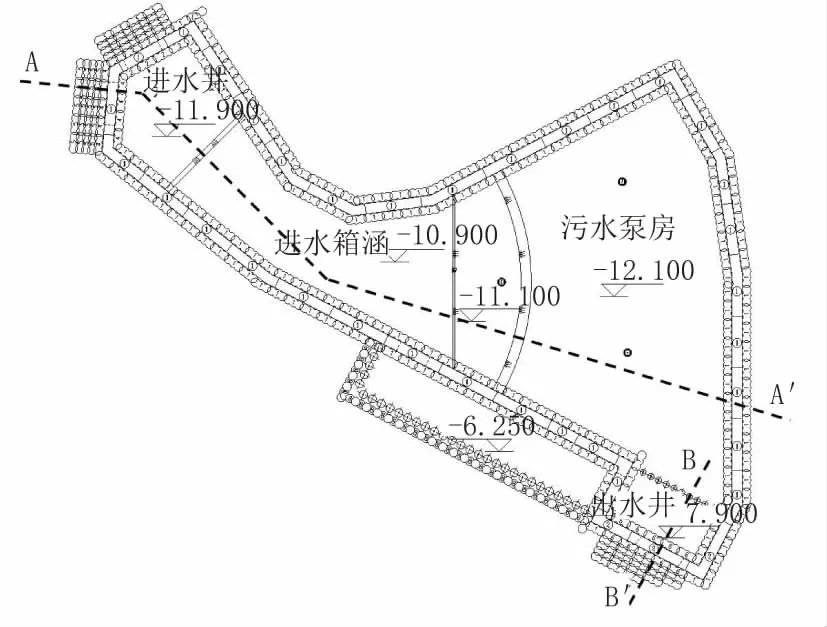
圖1 基坑平面圖（單位：m）

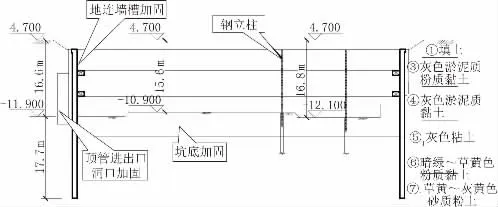
圖2 基坑A-A 剖面圖（單位：m）

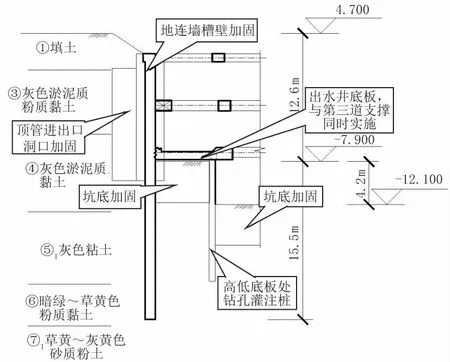
圖3 基坑B-B 剖面圖（單位：m）

基坑所處位置的土層參數如表2 所示。

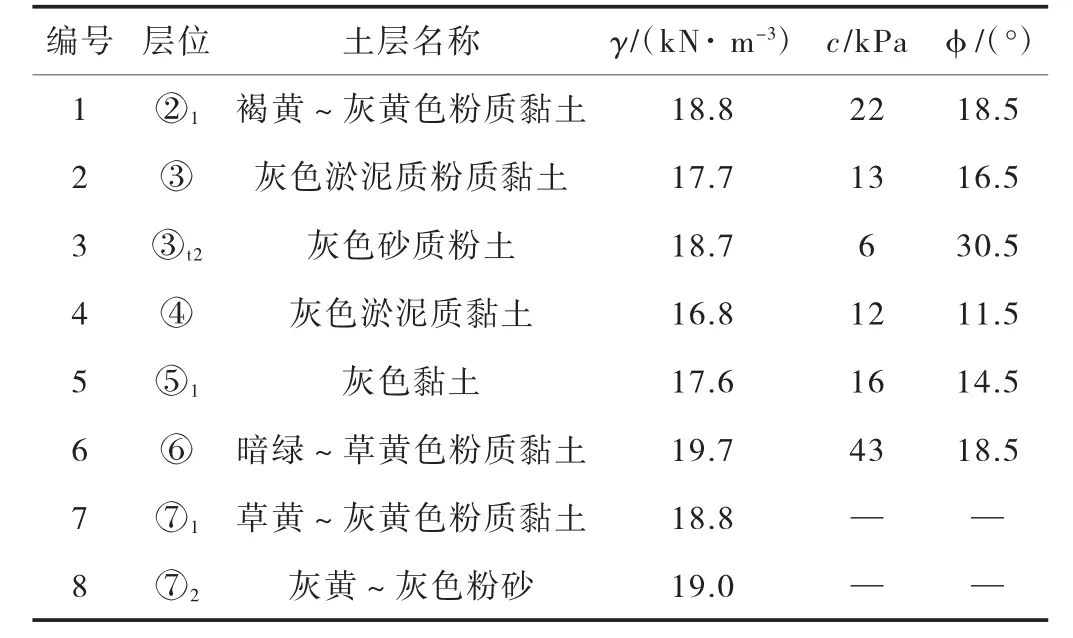
表2 地勘土體參數表

根據勘察報告所述，本基坑開挖過程中涉及上海第Ⅰ層承壓水層（第⑦層）的抗突涌問題，詳見圖4。

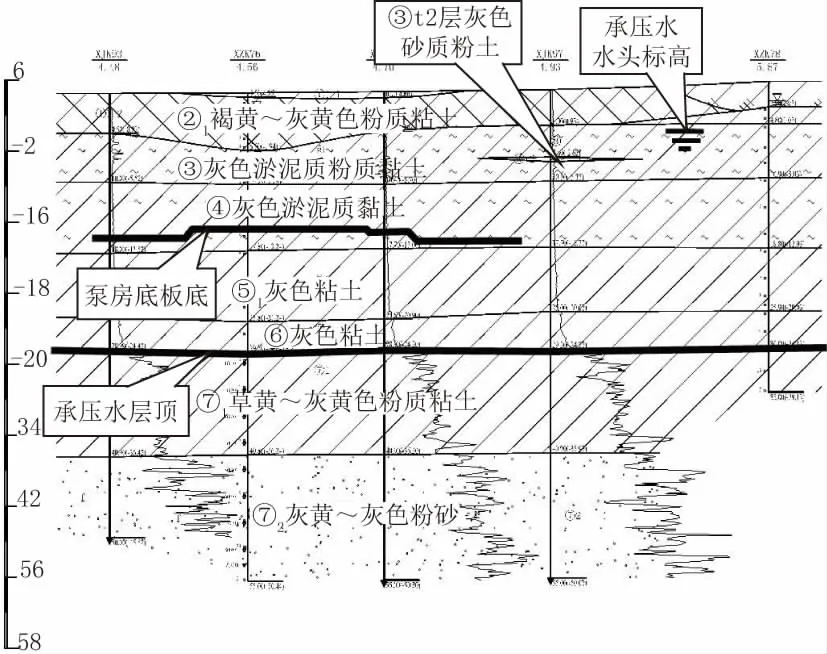
圖4 基坑地質剖面圖

根據勘察報告，擬建場地分布有⑦1層承壓含水層，承壓水水頭埋深年呈周期性變化，一般在3.0～12.0 m。根據上海市《基坑工程技術標準》（DGJ 08-61—2018）第6.7 節規定以及地勘報告，承壓水水頭埋深分別按實測和最不利因素考慮取4.7 m（絕對標高0.0）。對泵房基坑坑底抗⑦1層承壓水穩定性進行計算，結果如表3 所示。

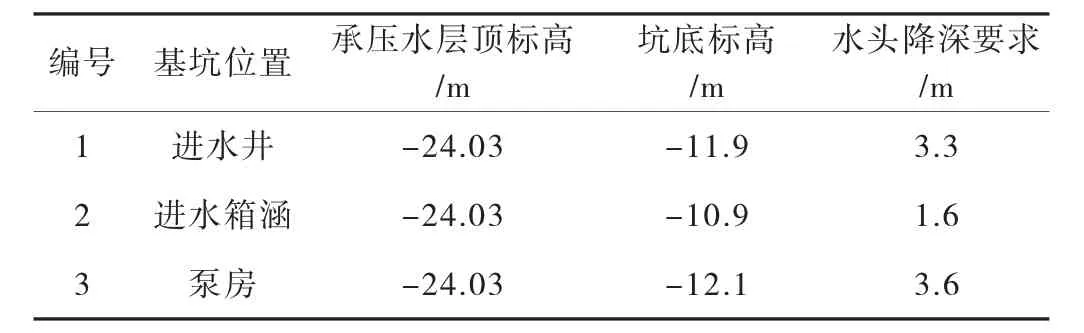
表3 坑底抗突涌穩定性驗算表

根據基坑底抗突涌分析，本工程泵房基坑坑底土體自重抗突涌不滿足要求，故需采取降承壓水措施。經計算，承壓水水頭需降低3.6 m（即絕對標高-3.6 m）可滿足抗突涌穩定。基坑降壓井布置如圖5 所示。

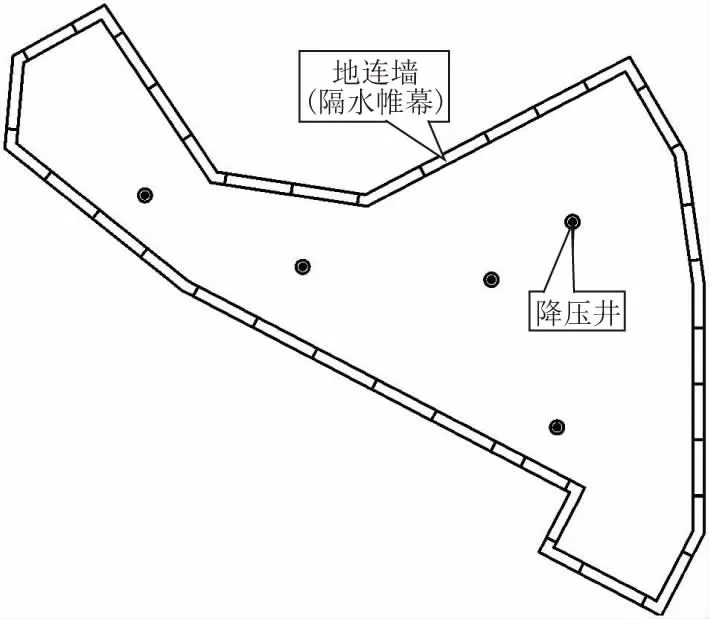
圖5 基坑降壓井布置圖

2.2 深基坑承壓水降壓分析

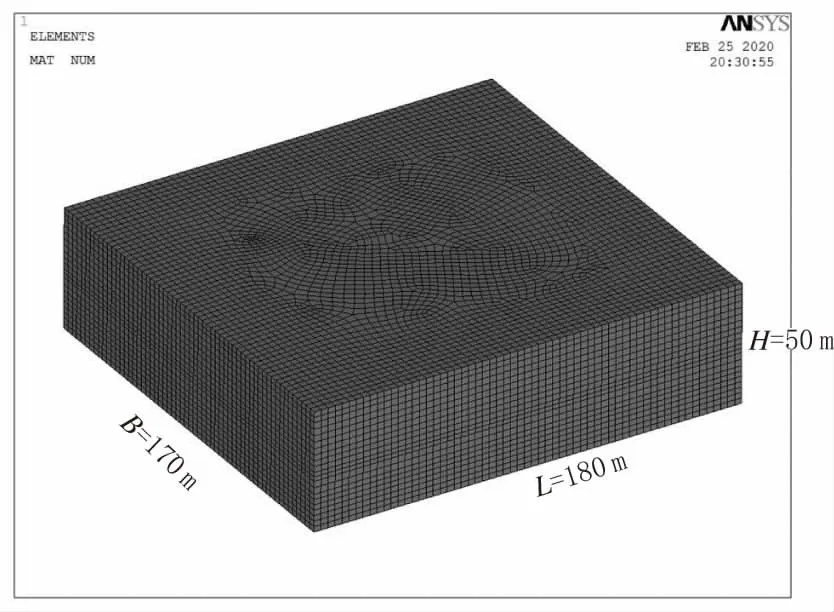
圖6 基坑土層模型（單位：m）

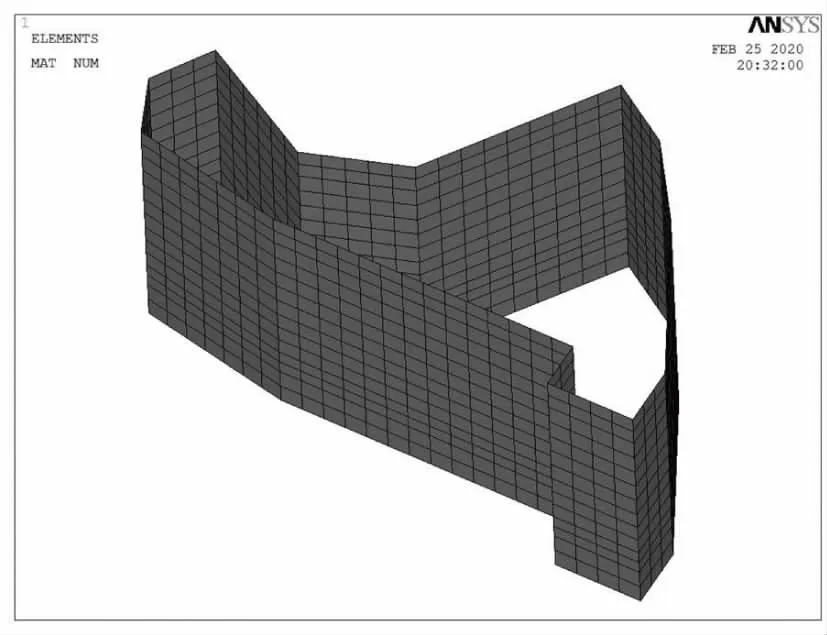
圖7 基坑地下連續墻（隔水帷幕）模型

由于本文采用熱模塊模擬滲流過程，單元的參數設置在理解上需要一定的轉換，基本計算參數見表4。

表4 滲流場與溫度場參數對照表

降壓井的設置本質上是邊界條件的設置，本文采用對承壓水層中降壓井部分的節點設置邊界條件，模擬抽水降壓的效果。根據上文的闡述，邊界條件分為兩類，對應降水井的設置為水頭控制與流量控制。其中流量控制需要較為準確的抽水試驗做依據，且無法考量土體降壓后出水量隨時間的波動，故不推薦使用。本文采用第一類邊界條件，即設置降壓井的總水頭值。本文假定承壓水層的總水頭值為0 m，總水頭由壓力水頭Hp 與位置水頭Hz 疊加而來。假設降壓井中的水第一時間被水泵抽走，則降壓井中的壓力水頭Hp 始終為0 m，則降壓井位于承壓水層部分的總水頭應設置為位置水頭Hz，Hz 在數值上等于節點標高減去承壓水水頭標高，假定位于承壓水層頂的降壓井標高為-29 m（地面標高為0 m），承壓水水頭標高為-4.5 m，則Hz=-24.5 m，節點邊界約束則定為-24.5 即可。需要注意的是，若采用真空管井抽水，則邊界條件在上述基礎上還需要減去13.6 m。

設置完所有參數后，采用瞬態分析，經過10～15 d 后，承壓水降壓后逐漸趨于穩定。穩定后承壓水層頂的總水頭分布如下圖所示，由于初始總水頭取0 m，故分布圖數值上也等于承壓水層頂總水頭的降深，且由于位置水頭沒有變化，故同時也等于壓力水頭的降深，其分布詳見圖8 所示。

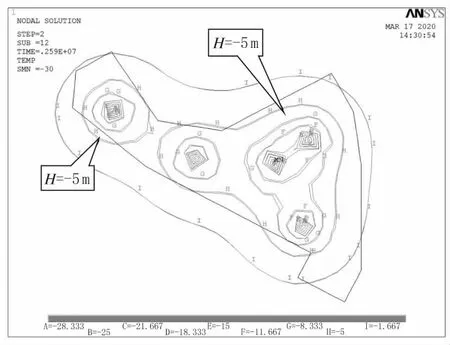
圖8 基坑承壓水降深分布（單位：m）

根據計算結果，除出水井部分區域，坑內降壓水頭均可達到5 m 以上，可以滿足表3 中壓力水頭降深要求，前提是降壓井中的水持續被抽出，以保證降壓井處的邊界條件與計算模型一致。

2.3 深基坑承壓水降壓對周邊環境影響分析

從ANSYS 熱分析模塊轉換到結構模塊是整個分析過程中的重點與難度，不論是操作上還是理解上。ANSYS 熱應力分析中，間接耦合法的邏輯是：首先得出模型的溫度變化分布，再通過結構分析中材料膨脹系數α 使得模型得到新的初始應變條件ε=α×ΔT。同時，轉換到結構模塊后，由于單元節點自由度發生變化，模型的邊界條件也要重新定義。上述做法“翻譯”到滲流—結構分析如下：首先通過滲流分析得到模型壓力水頭變化分布，壓力水頭的變化與水重度的乘積可以理解為承壓水層有效應力的變化，再通過結構分析中土體壓縮模量Es 使得模型得到新的初始應變條件很容易得到將定義到結構模型中的線膨脹系數參數即可得到承壓水層的初始固結應變。

因本文對于承壓水層初始固結及由此產生的上部土體變形均按線彈性考慮，故結構模型中的土體材料按線彈性考慮。各土層的壓縮模量按表5 所示。

表5 土層壓縮模量參數表

最后通過ANSYS 軟件結構模塊計算得到的地表沉降如圖9 所示，基坑承壓水降壓引起的地表沉降最大值約為20 mm，位于地連墻處，沉降值隨與基坑距離增大而減小，沉降槽近似漏斗形。

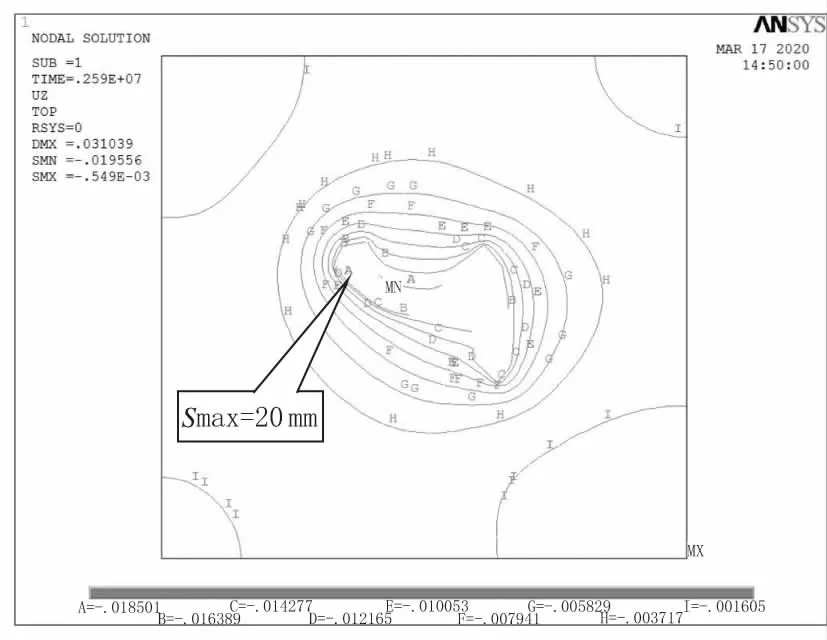
圖9 基坑降承壓水引起地表沉降分布（單位：mm）

2.4 不足與進一步工作展望

通常評價基坑施工對周邊環境影響程度須考慮降承壓水與基坑開挖兩種工況疊加的結果，目前由于基坑開挖模型更為復雜，不僅僅是空間模型本身（降水模型不包括支撐圍檁等構件，也無需定義開挖步），也包括更復雜的本構模型，難以與降水分析所采用的模型一致，故無法完全將兩者的模型的土體變形結果疊加，目前僅依靠粗糙的人工操作完成疊加工作，效率與準確性均難以令人滿意。

此外，在某些工程中，承壓水層與潛水層有一定水力聯系，降承壓水有可能導致潛水層的水位下降，故計算中需要考慮潛水降水的情況。對于ANSYS 軟件，降承壓水是線性的過程，降潛水是非線性的過程，主要是因為土體位于水位以上之后水頭不會再下降，故操作上需要采用迭代的方式更新潛水層的浸潤面，為了使得浸潤面平滑，需要更為細致的潛水層土體單元，故相較后僅計算承壓水降壓的過程，潛水降水計算效率較低。

針對上述困難，下一步的工作主要是：

（1）尋求兼顧效率與精度相統一的模型，同時包含基坑降水與開挖計算，或采用更為靈活準確的土體變形疊加方式，如采用直接耦合法或采用流-固耦合計算方法等；

（2）尋求解決潛水降水計算效率較低的方法。

3 結論

（1）本文論述了傳統深基坑設計中承壓水降壓對周邊環境影響分析方法的不足，包括降水與沉降計算的割裂、沉降計算方法不合理及對深基礎影響分析的局限性。

（2）本文通過ANSYS 10.0 通用有限元軟件模擬某基坑承壓水降壓過程，提供計算基坑承壓水降壓對周邊環境影響的計算方法。

（3）本文分析了現階段計算方法的兩點不足，主要包括難以建立統一的模型、疊加降承壓水過程與基坑開挖過程中對周邊環境影響的計算結果，也包括降潛水計算效率較低的問題。相應地，對下一步工作做出了展望。