基于灰色理論的中承式鋼箱拱橋主梁線形控制研究

卓小麗, 王 華, 劉國坤, 田仲初

(1.廣西交科集團有限公司, 廣西 南寧 530007； 2.湖南省交通科學研究院有限公司, 湖南 長沙 410015;3.長沙理工大學 土木工程學院, 湖南 長沙 410114)

0 引言

隨著我國交通建設的發展，鋼箱拱橋因其施工便利、周期短、環保等特點在橋梁結構的應用中頗受推崇，已有諸多學者對鋼箱拱橋的結構性能及結構設計方面進行了研究，劉中奇[1]以某三跨中承飛燕式鋼箱提籃式拱橋為工程背景，利用鋼箱拱橋Midas空間桿系模型以設計狀態為基準對施工狀態進行對比分析并不斷進行動態調整指導施工，控制結果得到了良好成效；許穎強[2]等以湖北香溪長江公路大橋為背景對大跨度鋼箱桁架拱橋拱肋架設施工技術進行了總結；周宇[3]等以廣東揭陽市區進賢門大橋無推力中承式提籃拱橋為背景，通過實體和板單元模型對其靜、動力性能進行了研究；陳耀章[4]等利用ANSYS建立了中承式拱橋鋼錨箱式錨固結構的"實-殼"混合彈塑性有限元模型，并通過對加勁板和支撐板長度、承壓板板厚等參數的敏感性分析，對中承式拱橋鋼錨箱式錨固結構的受力機理進行了研究；張濤[5]等對成都某鋼箱系桿拱橋進行了主梁溫度場的測試，分別研究了鋼箱梁溫差變形對主梁線形控制的影響和墩部溫差變形對線形控制的影響規律；田卿[6]等對漢口至陽邏江北快速路新河大橋中承式鋼箱提籃拱橋進行了設計，并利用有限元分析驗證了其安全可靠性；劉安興[7]采用Midas分析軟件對一大跨度下承式鋼箱提籃拱橋進行了力學性能分析及參數研究，并利用ANSYS建立了拱腳局部實體模型進行了受力分析；江京翼[8]等對大跨徑鋼箱桁架拱橋穩定性及影響因素進行了研究分析，探討了初始幾何缺陷對大橋的線彈性失穩荷載的影響。近年來，灰色預測理論在橋梁監測及施工控制方面也得到了大量應用;胡斌[9]等以一大跨徑懸臂澆筑施工剛構橋為工程背景，建立了GM(1，1)預測模型對施工過程中主梁線形預抬高值進行了預測，并利用實測數據進行了對比驗證，分析了預測模型的精度及其影響因素；劉歷波[10]等提出了一種基于馬爾科夫鏈修正的灰色GM(1，1)理論模型——灰色-馬爾科夫預測模型，并利用河北省數百座橋梁橋梁運營狀況的數據與灰色GM(1，1)理論模型進行了對比驗證分析，結果表明所提出的模型相較于灰色GM(1，1)理論預測模型具有更高的精度及穩定性；陳得意[11]等考慮異形拱橋拱肋旋轉及軸線偏差，建立了空間異形拱橋拱肋線形MGM(1，2)預測模型，并通過實測數據驗證了預測模型結果與實測數據吻合良好；哈娜[12]等針對橋梁結構的耐久性提出了灰色-馬爾科夫組合模型進行了預測，并通過遼寧省某橋的實測對比驗證了該模型的有效性。

基于以上研究成果，灰色預測理論在橋梁施工監測中的應用已逐漸嶄露頭角，但灰色理論在中承式鋼箱拱橋主梁施工過程中的應用卻鮮有報道。本文以廣西柳州市官塘大橋中承式鋼箱拱橋為依托背景，建立其節段施工考慮殘差修正的GM(1，1)預抬高值預測模型，對灰色預測理論在中承式鋼箱拱橋主梁施工線形控制中的應用展開研究。

1 工程概況

官塘大橋為中承式鋼箱拱橋，計算跨徑為457.183 m，計算矢跨比為1/4.5，凈跨徑為450 m，凈矢高為100 m，拱軸線平面與水平面夾角為80°，拱平面與豎直平面的夾角為10°，鋼箱拱肋截面寬度為5～5.012 m，截面高度為6.0～10.575 m，單個拱肋鋼箱劃分為27個吊裝節段；拱肋采用一字橫撐，橫撐沿拱肋徑向設置，全橋共計8道一字橫撐；主橋吊索采用φ15.2 mm、270級環氧涂層鋼絞線，單根直徑15.22 mm，標準強度1 860 MPa，吊索采用整束擠壓式錨具，材料選用40Cr；主梁為單箱單室扁平鋼箱梁，吊索區橋面全寬為44.5 m，無吊索區橋面全寬為39.5 m，主梁截面中心梁高為3.5 m(外輪廓)，全橋鋼箱梁劃分為44個節段，編號分別為1#～44#；分為6類，A類梁段為端節段，共2段；B、C類為無吊索區段，共4段；D類梁段為過渡節段，共2段；E類梁段為標準段，共35段；F類梁段為跨中段，共1段。鋼箱梁頂板及腹板厚為16 mm，底板及下斜板厚為12 mm。頂板在機動車道、非機動車道區域采用U肋進行縱向加勁，U肋上口寬為300 mm，底寬為170 mm，高為280 mm，板厚為8 mm，間距為600 mm。鋼箱梁在端頭靠近吊點的頂板區域(人行道區域)以及底板、下斜腹板均采用板式縱向加勁肋，加勁肋高為140 mm，板厚為12 mm，間距為350 mm。具體橋型布置圖及橫斷面圖如圖1、圖2所示。

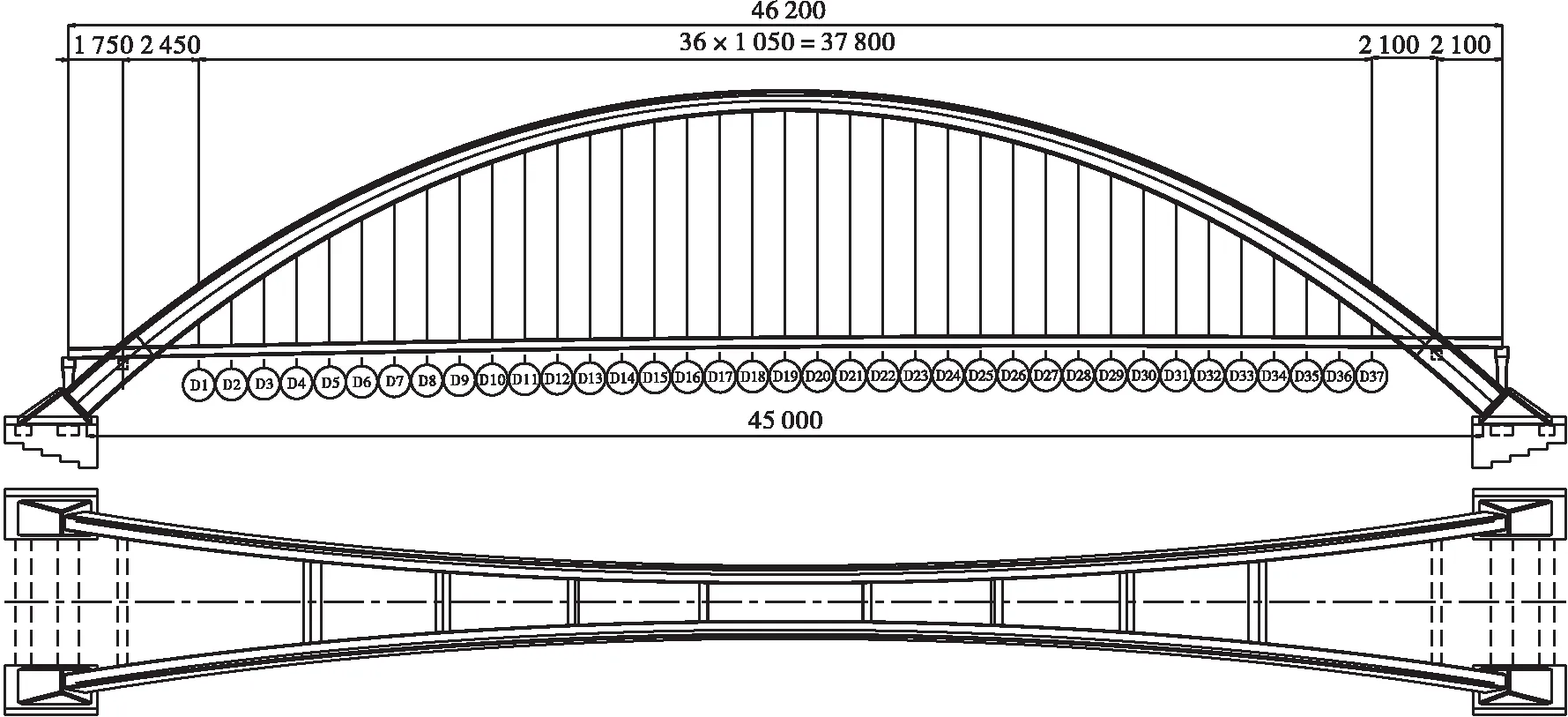
圖1 官塘大橋橋型布置圖(單位：cm)

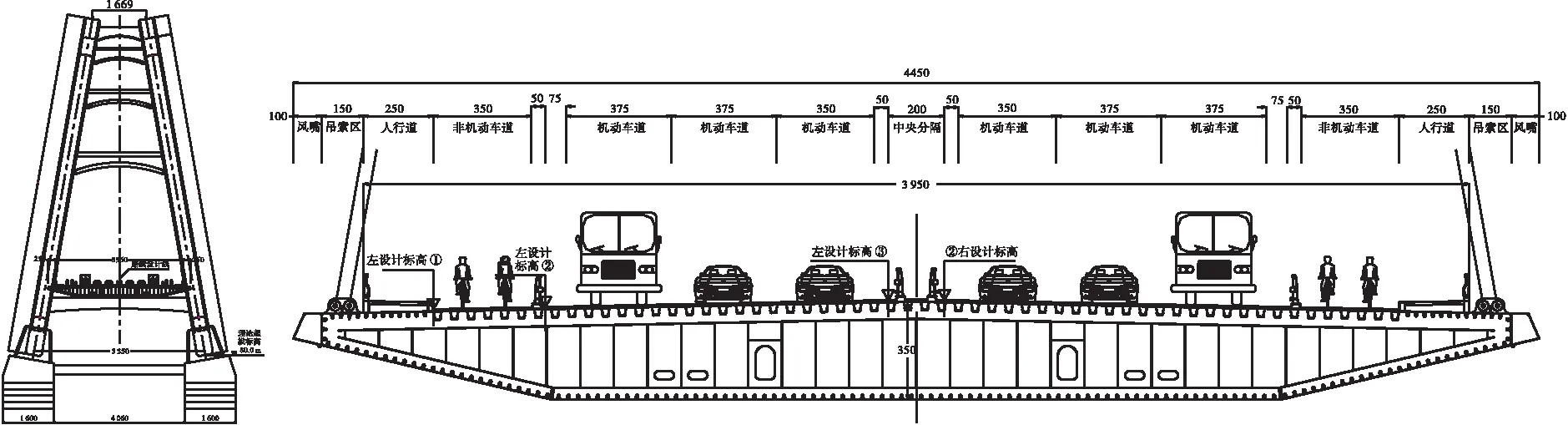
圖2 官塘大橋橫斷面布置圖(單位：cm)

2 灰色預測理論

2.1 GM(1，1)模型

我國華中科技大學鄧聚龍教授于1982年提出了灰色系統理論，完全已知為白，完全未知為黑；而灰色系統則是部分已知、部分未知的系統。灰色方程稱為GM模型，由Grey(灰)及Model(模型)的首字母縮寫構成，G(1，N)前面的“1”代表模型階數為一階，后面的“N”代表模型包含N個變量，GM(1，1)模型則代表一階單變量的微分方程模型。灰色方程GM(1，1)的具體建立過程如下。

給某一等時間隔的非負數據列{k，x(k)}：

{k，x(k)}=(1，x1)，

(2，x2)…(n，xn)

(1)

式中：k代表時刻；x(k)=xk代表t=k時刻時某量的觀測值。非負數列x(0)代表某量的原始數據序列，如式(2)所示。

(2)

現對原始數據x(0)進行一次累加生成處理，如式(3)所示。

(3)

得到原始數據序列一次累加生成數據序列為X(1)：

(4)

經原始非負數據序列一次累加所生成的累加數序列X(1)具有更強烈的單調性。能近似看做是指數的，可通過指數型曲線進行線形擬合。現利用指數曲線來擬合具有強烈單調性的累加生成序列X(1)，則一定可以用某一階線性常系數微分方程來表示這條指數擬合曲線：

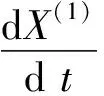
(5)

則有：

(6)

即:

(7)

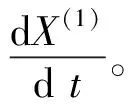
(8)

Δt代表時間間隔，并認為時間可被充分細化，現將時間間隔Δt當成單位時間間隔。則有：

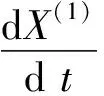
(9)

故式(5)可近似為：

x(0)(k+1)+aX(1)(t)≈u，(k≤t≤k+1)

(10)

式(10)中函數X(1)(t)為對應區間[k，k+1]上的某一取值，并用區間中值近似表達有：

(11)

則式(5)最終可近似簡化成式(12)：

(12)

由式(12)可看出，該式為關于待確定參數a和u的一個線性近似表達式。故數據點(xi，yi)由式(12)可轉化為：

yi≈axi+b

(13)

根據最小二乘原理，a和b作為線性回歸系數可按式(14)進行求解：

(14)

式中：

(15)

由式(15)可知，當有n個原始數據時，則有n-1個依次累加而生成的數據。

最終有一階微分方程的解為：

(16)

式(16)就是最后得到的預測模型，該模型稱作GM(1，1)預測模型。上述各式中a代表了GM(1，1)模型發展系數，反映了x(0)和X(1)的發展態勢；u代表了灰色作用量，反映了數據變化的關系。

則還原值：

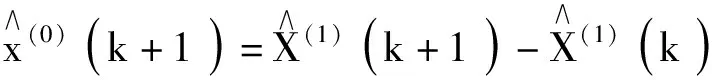
(k=1，2，…，N)。

2.2 殘差GM(1，1)模型

當GM(1，1)模型精度尚未達到精度要求時，可通過殘差序列建立GM(1，1)模型對原有GM(1，1)模型進行修正。

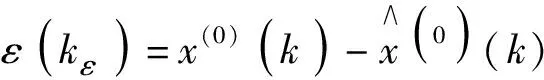
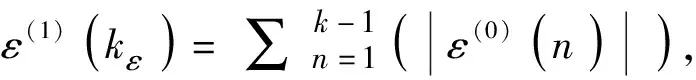
同式(5)有：

(17)

其時間響應式為：

(18)

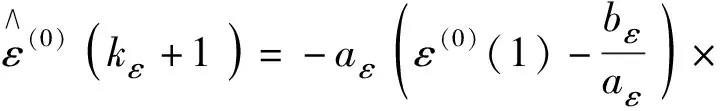
e[-aε(kε-1)]，kε≥1

(19)

還原式殘差修正模型如式(20)所示：

(20)

3 灰色預測模型的建立

3.1 初步預抬高值的預測

廣西柳州市官塘大橋中承式鋼箱拱橋主梁施工時的理論立模標高僅僅為理論分析計算模型數據，而因現場實際施工時的立模標高需考慮更多不確定因素，例如溫度、施工荷載、彈性變形、天氣及焊接工藝等；故理論分析計算值與現場實測數據有些許差異，需對理論立模標高進行適當修正。

令實測預抬高值序列為：Y=[Y(1)，Y(2),…，Y(N)]；令理論分析預抬高值序列為：Y′=[Y′(1)，Y′(2)，…，Y′(N)]；式中N為主梁施工階段數。灰色模型誤差X(0)(k)=Y(k)-Y′(k)+C;k=1，2，…,k，N，C=max|Y(k)-Y′(k)|。根據Y、Y′建立其灰色模型誤差序列：X(0)=[X(0)(1)，X(0)(2)，…，X(0)(N)]。

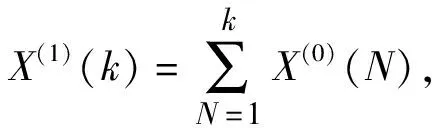
(21)

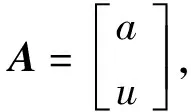
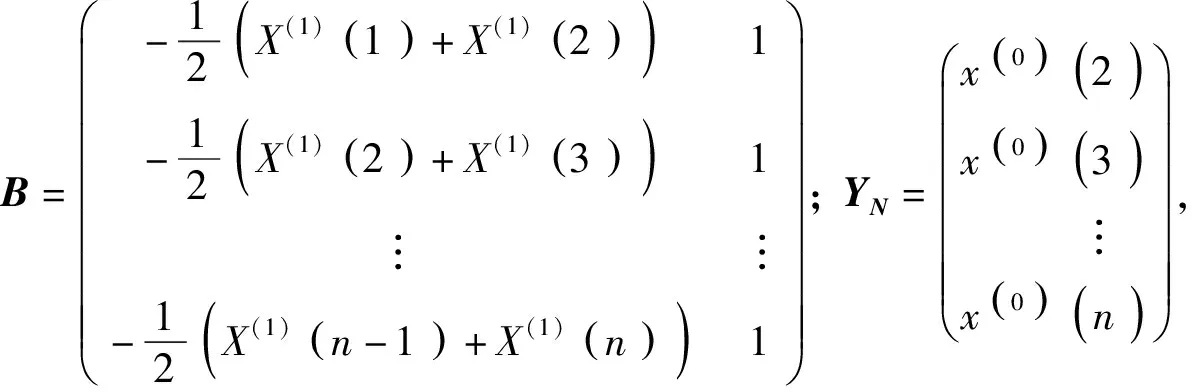
3.2 殘差GM(1，1)模型預抬高值修正預測

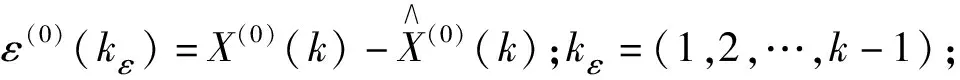
根據2.2節有：

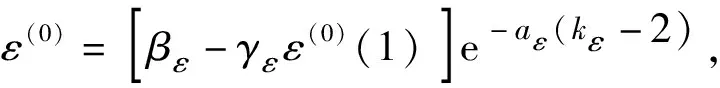
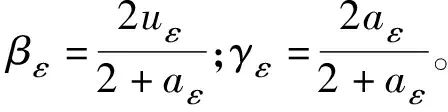
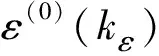
(22)

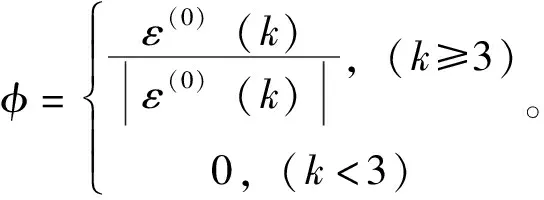
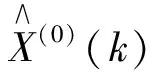
(23)

3.3 各主梁節段立模標高的確定

由前述3.1、3.2綜合可得，經殘差修正過后第k個主梁節段的立模標高如式(24)所示：

(24)

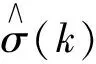
基于上述計算流程，根據理論分析計算預抬高值及現場實測數據，采用MATLAB編制廣西柳州市官塘大橋主梁施工過程的立模標高灰色預測模型計算程序，預測主梁安裝下個節段的立模標高，具體分析流程圖見圖3。

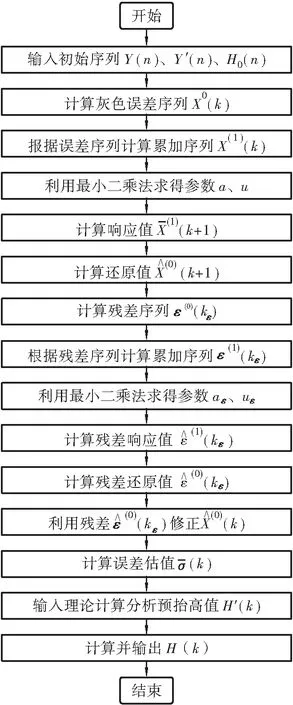
圖3 主梁節段立模標高灰色預測模型計算流程圖

4 有限元模型的建立

為研究灰色中承式鋼箱拱橋主梁施工線形控制中預測理論的應用，以廣西柳州市官塘大橋中承式鋼箱拱橋為依托背景，建立了結構有限元仿真計算分析模型，通過有限元仿真計算分析模型求得官塘大橋主梁施工過程中各節段理論預抬高值，模型共劃分為453個單元，520個節點，采用梁單元來實現主梁及肋間橫撐的模擬，采用僅受拉桁架單元來進行吊桿的模擬；拱腳處采用固定約束，拱梁連接處采用彈性連接進行模擬；模型荷載作用考慮了結構自重、二期及施工臨時荷載等，其中施工階段臨時荷載考慮了橋面吊機荷載，采用節點荷載進行模擬。相關材料參數表見表1，具體仿真計算分析模型如圖4所示。

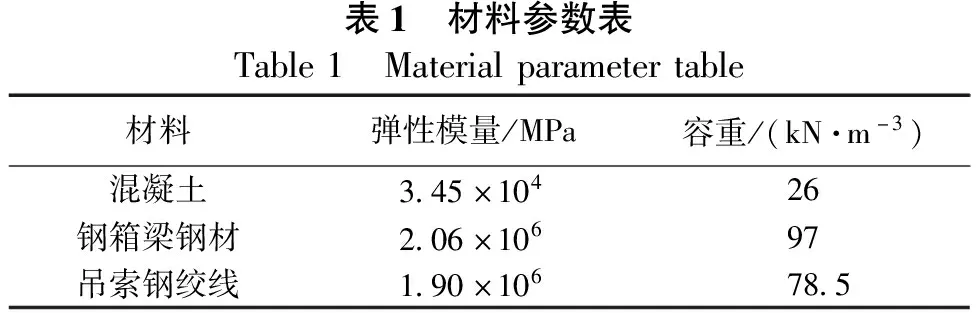
表1 材料參數表Table1 Materialparametertable材料彈性模量/MPa容重/(kN·m-3)混凝土3.45×10426鋼箱梁鋼材2.06×10697吊索鋼絞線1.90×10678.5

圖4 官塘大橋仿真計算分析模型圖

根據上述所建立結構仿真計算模型，考慮主梁施工過程中各施工荷載因素得到了主梁各節段前端頂面中心施工階段預抬值如表2所示。(僅考慮有吊桿的階段即E類標準節段)

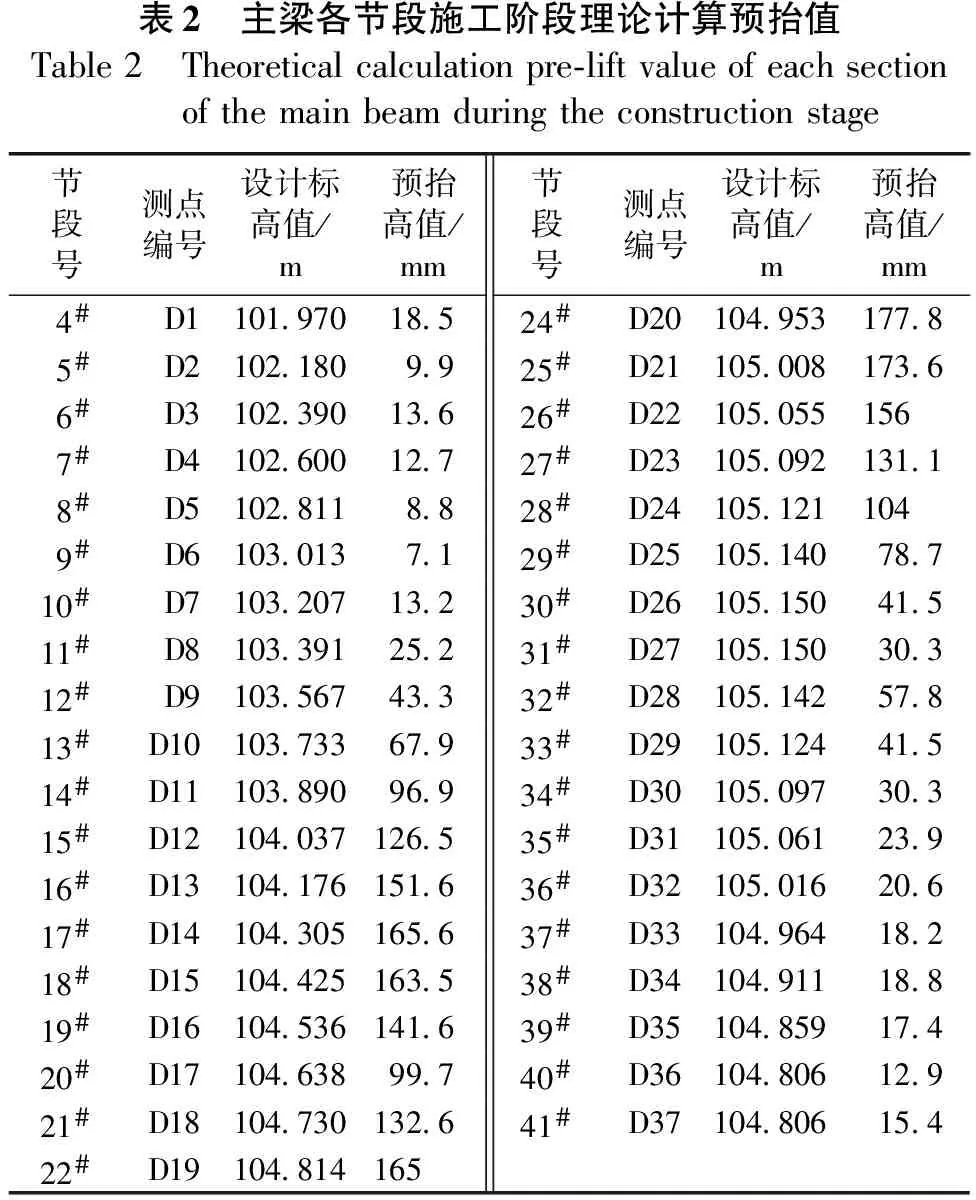
表2 主梁各節段施工階段理論計算預抬值Table2 Theoreticalcalculationpre-liftvalueofeachsectionofthemainbeamduringtheconstructionstage節段號測點編號設計標高值/m預抬高值/mm節段號測點編號設計標高值/m預抬高值/mm 4# D1101.97018.524#D20104.953177.8 5# D2102.1809.925#D21105.008173.6 6# D3102.39013.626#D22105.055156 7# D4102.60012.727#D23105.092131.1 8# D5102.8118.828#D24105.121104 9# D6103.0137.129#D25105.14078.710# D7103.20713.230#D26105.15041.511# D8103.39125.231#D27105.15030.312# D9103.56743.332#D28105.14257.813#D10103.73367.933#D29105.12441.514#D11103.89096.934#D30105.09730.315#D12104.037126.535#D31105.06123.916#D13104.176151.636#D32105.01620.617#D14104.305165.637#D33104.96418.218#D15104.425163.538#D34104.91118.819#D16104.536141.639#D35104.85917.420#D17104.63899.740#D36104.80612.921#D18104.730132.641#D37104.80615.422#D19104.814165

5 灰色模型預測結果驗證分析

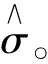
利用MATLAB編制的廣西柳州市官塘大橋主梁施工過程的立模標高灰色預測模型計算程序以每4個節段滾動預測求解下一節段立模標高(即以k#～k+3#節段的理論與實測數據預測k+4#節段的立模標高)，并與節段施工完成后實測標高進行對比。立模標高的確定主要決定于節段預抬值的確定，現將8#～40#主梁預抬高值的預測結果及實測數據整理如表3所示。預測預抬高值與實測及理論預抬高值的對比曲線如圖5所示。

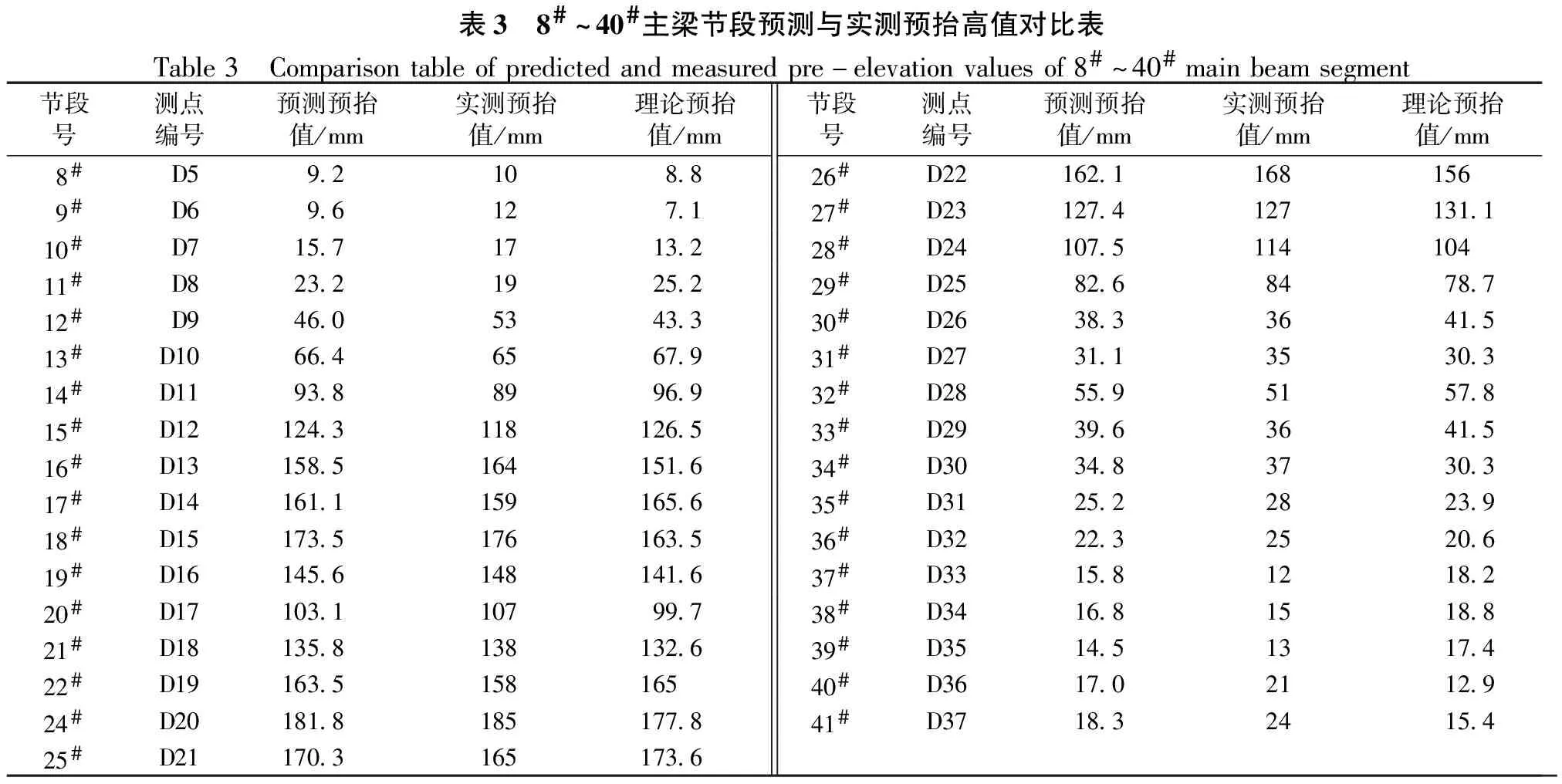
表3 8#～40#主梁節段預測與實測預抬高值對比表Table3 Comparisontableofpredictedandmeasuredpre-elevationvaluesof8#～40#mainbeamsegment節段號測點編號預測預抬值/mm實測預抬值/mm理論預抬值/mm節段號測點編號預測預抬值/mm實測預抬值/mm理論預抬值/mm 8# D59.2108.826#D22162.1168156 9# D69.6127.127#D23127.4127131.110# D715.71713.228#D24107.511410411# D823.21925.229#D2582.68478.712# D946.05343.330#D2638.33641.513#D1066.46567.931#D2731.13530.314#D1193.88996.932#D2855.95157.815#D12124.3118126.533#D2939.63641.516#D13158.5164151.634#D3034.83730.317#D14161.1159165.635#D3125.22823.918#D15173.5176163.536#D3222.32520.619#D16145.6148141.637#D3315.81218.220#D17103.110799.738#D3416.81518.821#D18135.8138132.639#D3514.51317.422#D19163.515816540#D3617.02112.924#D20181.8185177.841#D3718.32415.425#D21170.3165173.6

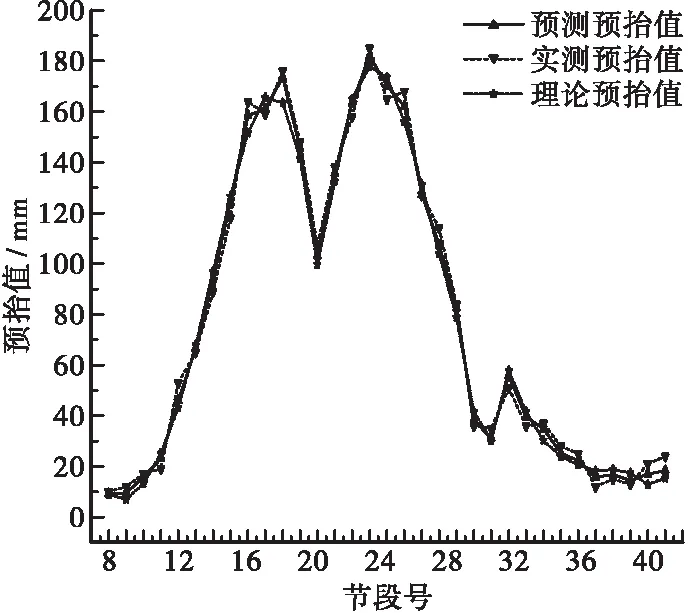
圖5 預抬高值對比曲線表

由表3及圖5分析可知，各節段實測預抬值與理論預抬值最大偏差(理論值-實測值)為-12.5 mm，最大偏差率[(理論值-實測值)/實測值×100%]為51.7%；利用灰色模型GM(1，1)滾動預測出的預抬值與實測預抬值的最大偏差(預測值-實測值)為-7 mm，最大偏差率[(預測值-實測值)/實測值×100%]為31.7%；預測預抬值與實測預抬值更接近，且各節段預抬值絕對誤差不超過10 mm。經實測驗證，考慮殘差修正的GM(1，1)模型在廣西柳州市官塘大橋主梁施工過程主梁線形預測效果良好，預測模型魯棒性高。

施工過程中引入殘差修正的GM(1，1)模型預測整個主梁(8#～41#)各節段立模標高，并嚴格控制主梁施工線形指導現場施工，現將成橋狀態主梁理論線形、實測線形及預測線形對比圖整理如圖6所示。

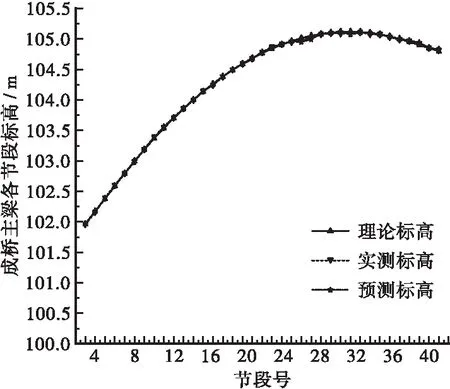
圖6 成橋狀態主梁線形對比圖

經對比分析有，成橋狀態主梁實測線形與理論線形各節段最大偏差為34.5 mm，成橋狀態主梁實測線形與預測線形各節段最大偏差為29.8 mm，由圖6分析可知，主梁預測線形與實測線形吻合度高，驗證了殘差修正的GM(1，1)模型在廣西柳州市官塘大橋主梁施工過程主梁線形預測的精度較高，可在中承式提籃拱橋鋼箱主梁實際施工中推廣使用。

6 結論

本文以廣西柳州市官塘大橋中承式鋼箱拱橋為依托背景，建立了考慮殘差修正的主梁施工線形灰色預測模型GM(1，1)，并利用現場實測數據對模型進行了對比驗證，研究了灰色理論在中承式鋼箱提籃拱橋主梁施工過程中線形預測與控制中的應用。具體結論可總結如下：

a.主梁施工過程中預測預抬值與實測預抬值偏差最大僅7 mm，最大偏差率為31.7%;而實測預抬值與理論預抬值最大偏差為12.5 mm，最大偏差率為51.7%，預測預抬值與實測預抬值契合度高，精度良好。

b.成橋狀態下主梁預測線形與實測線形吻合良好，相較于理論線形更為貼近，驗證了考慮殘差修正的灰色預測模型在中承式鋼箱提籃拱橋主梁施工過程中應用的可行性及穩定性，可做推廣使用。