自錨式懸索橋拉-吊體系轉換主纜位移特性分析

吳海軍，何 立，郭 輝，王邵銳，王 楨

(1.重慶交通大學，重慶 400074； 2.省部共建山區橋梁及隧道工程國家重點實驗室，重慶 400074; 3.鐵科院(北京)工程咨詢有限公司，北京 100081)

自錨式懸索橋造型美觀、結構新穎，景觀及造型上的優勢使這種橋型發展迅速[1-3]。自錨式懸索橋傳統施工法通常需要搭設支架或臨時墩實現主梁安裝及體系轉換，對施工現場的地形條件有較高要求，這限制了自錨式懸索橋的發展[4-6]，而“先斜拉，后懸索”(即先采用斜拉扣掛法安裝主梁，形成臨時斜拉橋；再架設主纜、張拉吊索，形成“斜拉-懸索”共存體系；最后拆除斜拉索，形成懸索橋)施工法能有效解決此難題，該方法在2019年即將建成的鵝公巖軌道專用橋中得到首次應用。鵝公巖軌道專用橋是主跨為600 m的自錨式懸索橋，即將超越當前已建成的主跨為480 m的世界最大跨徑自錨式懸索橋——愛沙尼亞穆胡島橋而成為新的世界之最。鵝公巖軌道專用橋主跨為長江主航道，為了確保長江正常通航，防止船只撞上橋梁支架，鵝公巖軌道專用橋不能在長江航道里搭建支架或頂推成梁，因而首次采用“先斜拉，后懸索”的總體施工方案，運用斜拉扣掛施工法實現體系轉換，施工方法新穎、獨特，體系轉換技術難度高，轉換過程中，結構受力、變形過程復雜，國內外工程界尚無成熟經驗可以直接應用，相關研究也極少。

目前，針對大跨徑自錨式懸索橋主纜位移特性已有部分學者進行了相關研究，如檀永剛[7]等提出自錨式懸索橋主纜弱相干性原理，并通過金華康濟橋進行了實橋論證；張俊平[8]等通過模型試驗研究了獵德大橋主纜位移在體系轉換過程中的演變規律，并明確指出了主纜弱相干性特性的適用條件；王楨[9]等采用模型試驗與數值模擬相結合的方法分析了桃花峪黃河大橋主纜隨施工階段的變化規律，對主纜弱相干性適用條件進行了探討。但以往的研究均是基于傳統的體系轉換方式，而工程界對“先斜拉，后懸索”體系轉換過程中主纜位移變化規律及幾何非線性行為表現等認識不夠深入和全面，特別是當主跨跨徑從400 m級突破至600 m級時，其結構體系力學特性將發生質的變化，且隨著跨徑不斷增大，其幾何非線性亦更加突出。有鑒于此，本文以鵝公巖軌道專用橋為依托，研究大跨自錨式懸索橋在“先斜拉，后懸索”體系轉換過程中主纜的位移變化規律，以期為同類型橋梁的建設提供參考。

1 工程概況

鵝公巖軌道專用橋主橋跨徑布置為(50+210+600+210+50)m，為雙塔五跨自錨式懸索橋，橋跨布置如圖1。主梁為鋼-混混合梁，主纜錨固段及錨跨段采用預應力混凝土結構，混凝土箱梁與鋼箱梁之間設鋼-混結合段，邊跨鋼箱梁采用頂推法施工，中跨鋼箱梁采用斜拉扣掛懸臂拼裝施工法，鋼箱梁標準節段梁長15 m。主纜矢跨比為1/10，主纜采用高強平行鋼絲束，標準強度為1 860 MPa，纜間距為19.5 m;吊桿采用高強平行鋼絲束，標準強度為1 770 MPa，吊桿間距為15 m。兩岸主塔高度一致，均為鋼筋混凝土門形構造。

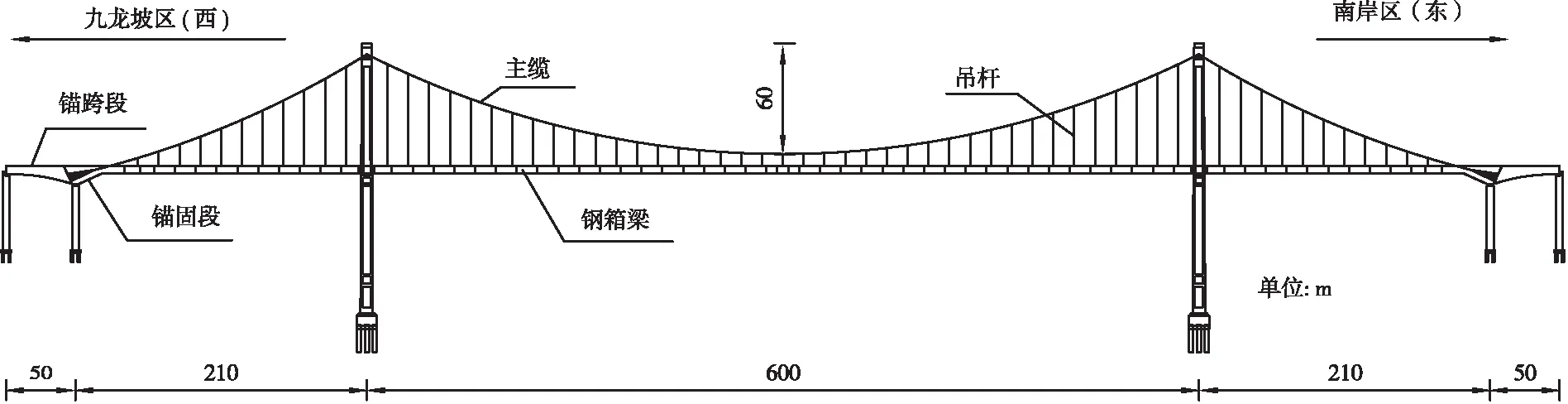
圖1 鵝公巖軌道專用橋全橋橋跨布置圖

2 數值模型

采用MIDAS/Civil對“斜拉-懸索”體系轉換過程進行仿真模擬。結合本橋實際情況，在數值模擬中，主梁、主塔采用變截面梁單元模擬，臨時斜拉索、主纜及吊桿采用索單元模擬；主塔塔底固結，主梁于主塔處約束其豎向及橫向自由度，主纜錨固點與加勁梁之間采用剛性連接，臨時支架采用只受壓不受拉彈性支撐模擬。有限元分析模型見圖2。

圖2 MIDAS Civil 有限元模型

3 主纜位移特性分析

自錨式懸索橋“斜拉-懸索”體系轉換最終目標是使成橋線形和受力均符合設計要求，并保證體系轉換過程中結構安全。吊索的張拉順序、臨時斜拉索的拆除時機及順序等使“斜拉-懸索”體系轉換方式錯綜復雜，但體系轉換方式是否合理應從施工便利性、安全性、經濟性等方面綜合進行考慮。本文所采用的體系轉換程序是綜合以上原則而設置，在整個施工過程中各構件受力及變形均符合要求。

體系轉換總體思路：以臨時斜拉橋為基礎，從主塔向跨中方向安裝數對能一次張拉到位的吊索；然后中跨繼續向跨中方向安裝吊索，與此同時，從主塔向錨跨方向安裝邊跨吊索，一側1根，對稱安裝，直至體系轉換完成；再從上至下逐對拆除臨時斜拉索，以此實現體系轉換。

鵝公巖軌道專用橋橋跨布置對稱，在施工過程中主纜變形基本對稱，故僅提取左半跨(九龍坡區側)主纜位移數據進行分析。懸索橋吊索編號及臨時斜拉橋拉索編號見圖3，體系轉換方案施工工序見表1。

圖3 “斜拉-懸索”體系共存圖

3.1 主纜位移變形特性分析

為研究主纜位移在各施工階段的變化規律，選取了左半跨(九龍坡區側)部分吊索對應主纜索夾點(以下簡稱吊點)進行位移特性分析，其變化規律見圖4，圖中“豎向位移累積量”指在當前施工階段吊索對應主纜索夾點產生的豎向位移累積量。分析結果如下。

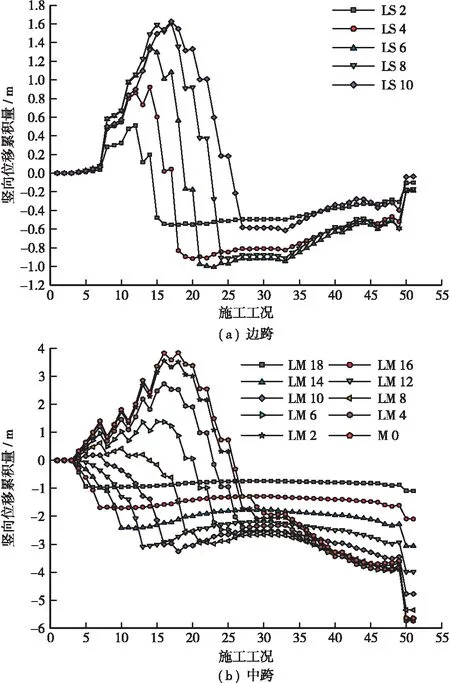
圖4 邊、中跨主纜豎向位移累積量/m

a.近塔區和主纜錨固區主纜吊點(如LS2、LS10、LM18、LM16)豎向位移波動范圍明顯小于其他吊點。這是由于近塔區及主纜錨固區的主纜分別受主塔與錨固段的約束作用，主纜的豎向剛度較大，致使該區段主纜豎向變形較小。

b.主索鞍頂推使得兩個塔頂主索鞍之間的水平投影長度減小，邊跨主纜水平投影長度變大，使中跨主纜呈現出“松弛”狀態，而邊跨主纜呈現“緊繃”現象，邊跨主纜在主索鞍頂推工況均發生了豎直向上位移，中跨主纜位移變化與之相反，如工況8、工況11等。這主要是因為懸索橋施工中鞍座頂推的目的是釋放鞍座底由于橋塔縱向剛度約束引起的縱向剪力，避免橋塔受力過大和主纜在鞍座中的滑移，一般懸索橋鞍座頂推前后主纜線形變化不大，但由于本橋先施工了斜拉橋，在張拉吊索時，塔頂的剛度大，塔頂的變形小，鞍座頂推的目的主要是釋放鞍座兩側的不平衡力，由此才出現頂推前后主纜線形變化比較大的問題，也即呈現出邊跨主纜“緊繃”，中跨主纜“松弛”現象。

c.邊跨主纜吊點在拆臨時斜拉索階段均產生了緩慢向上變形的趨勢，這是由于臨時斜拉索拆除時機位于全橋吊桿張拉結束后，此時加勁梁的絕大部分重量通過吊桿已轉移至了主纜，主纜的重力剛度初步形成，因此在拉索拆除階段，主塔兩側主纜的不平衡水平力較小，主塔向跨中發生了較小的側移，使邊跨主纜發生了較小的向上變形量，中跨主纜豎直向下變形逐漸減小且趨于穩定。此過程中，應根據塔根應力及塔頂側移及時進行主索鞍頂推，保證主塔安全。

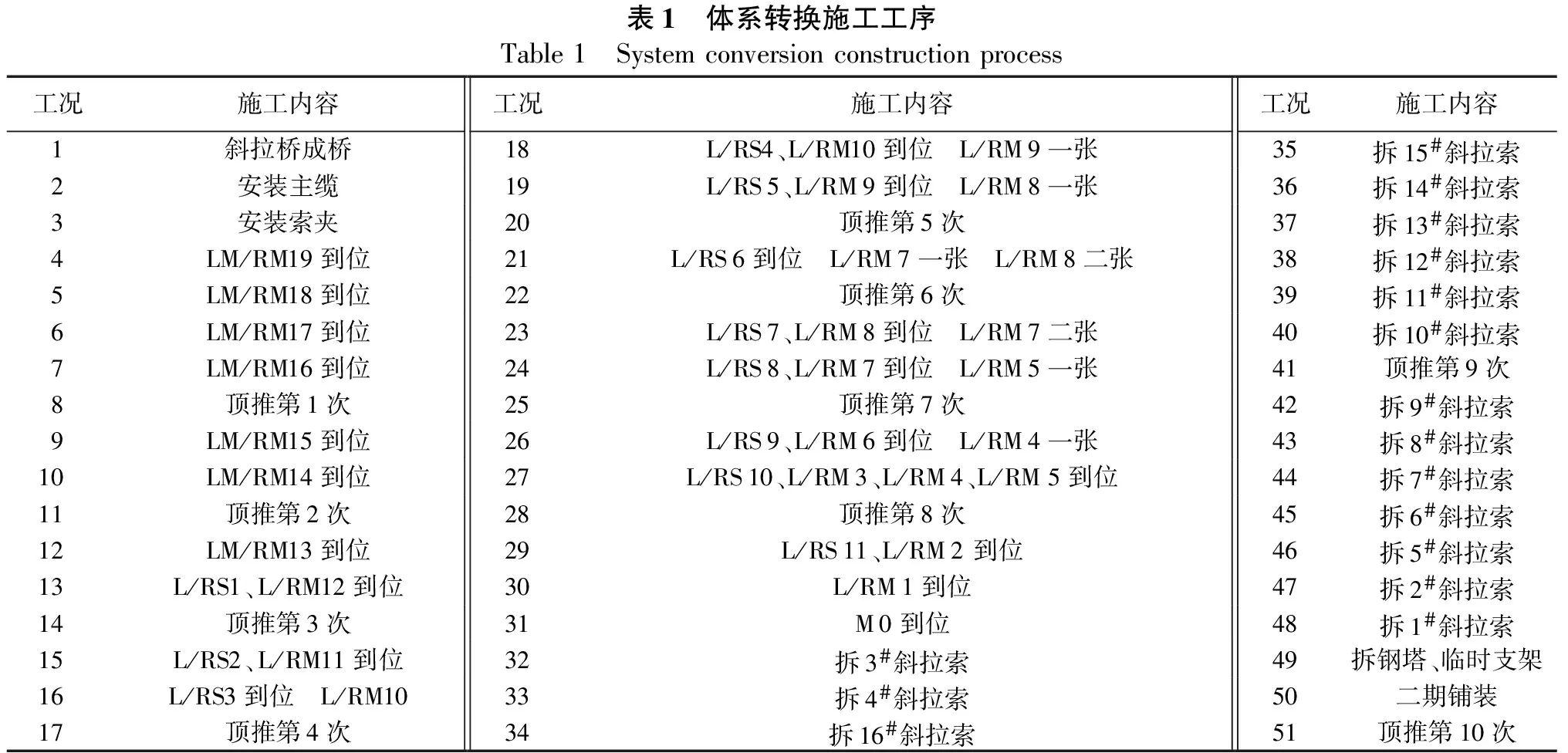
表1 體系轉換施工工序Table1 Systemconversionconstructionprocess工況施工內容工況施工內容工況施工內容1斜拉橋成橋18L/RS4、L/RM10到位 L/RM9一張35拆15#斜拉索2安裝主纜19L/RS5、L/RM9到位 L/RM8一張36拆14#斜拉索3安裝索夾20頂推第5次37拆13#斜拉索4LM/RM19到位21L/RS6到位 L/RM7一張 L/RM8二張38拆12#斜拉索5LM/RM18到位22頂推第6次39拆11#斜拉索6LM/RM17到位23L/RS7、L/RM8到位 L/RM7二張40拆10#斜拉索7LM/RM16到位24L/RS8、L/RM7到位 L/RM5一張41頂推第9次8頂推第1次25頂推第7次42拆9#斜拉索9LM/RM15到位26L/RS9、L/RM6到位 L/RM4一張43拆8#斜拉索10LM/RM14到位27L/RS10、L/RM3、L/RM4、L/RM5到位44拆7#斜拉索11頂推第2次28頂推第8次45拆6#斜拉索12LM/RM13到位29L/RS11、L/RM2到位46拆5#斜拉索13L/RS1、L/RM12到位30L/RM1到位47拆2#斜拉索14頂推第3次31M0到位48拆1#斜拉索15L/RS2、L/RM11到位32拆3#斜拉索49拆鋼塔、臨時支架16L/RS3到位 L/RM1033拆4#斜拉索50二期鋪裝17頂推第4次34拆16#斜拉索51頂推第10次

d.在體系轉換過程中，中跨主纜豎向位移變形范圍較大，邊跨主纜豎向位移變形范圍相對較小。這主要是因為中跨主纜的豎向位移是主索鞍頂推產生的“松弛”效應和吊索張拉效應的疊加，而邊跨主纜豎向位移與之相反，加之邊跨矢跨比較中跨小，邊跨豎向剛度較中跨大，因此中跨主纜豎向變形表現較邊跨更加劇烈。

3.2 主纜位移幾何非線性行為分析

大跨徑自錨式懸索橋主纜的幾何非線性問題尤為突出，研究非線性的方法較多[10-12]，本文采用最為直接的方法-分次加載法對此橋施工過程中主纜幾何非線性特征進行分析。分次加載法是以荷載作用不發生改變為原則，探求結構響應的變化規律。具體陳述為在同一結構體系中、同一施工工序下，將同一位置的作用荷載均分為兩份，連續兩次作用于結構，對比主纜位移的增量。若兩次增量相同，則主纜位移呈線性特征；否則，主纜位移呈幾何非線性特征。

3.2.1吊索張拉過程中主纜幾何非線性行為表現

圖5中“兩次荷載作用位移差值”指將作用荷載均分為兩份并連續作用于結構上時，主纜兩次豎向位移增量的差值；各施工工況詳見表1；吊點編號為左半跨吊索對應主纜上的索夾點編號，吊點編號按LS11→M0方向依次為2～33；下同，不再贅述。

圖5(a)中，施工工況4～工況12主要為對稱張拉中跨近塔處的吊索，張拉次序為：LM19→LM13，即從塔根向跨中方向張拉。在此過程中，邊跨主纜豎向位移差值最大值從0.2 cm漸漸增至0.7 cm，位移差值的變化量微小；中跨主纜的豎向位移差值最大值隨著施工工況的進行從2.1 cm逐漸增加至6.9 cm。以此可知，在施工工況4～工況12過程中，邊跨主纜位移幾何特性呈現出顯著的線性表現形式，但隨著施工的進行，線性特征略有衰減；中跨主纜位移線性特性隨著吊索的張拉而漸漸弱化。

圖5(b)中，施工工況13～工況31為對稱張拉邊、中跨吊索，張拉順序為：LS1/LM12→LS11/LM2→LM1→M0。在此期間，邊跨主纜豎向位移差值最大值變化歷程為：3.7 cm→9.1 cm→0 cm；中跨主纜豎向位移差值最大值變化歷程為：10.2 cm→20.9 cm→0 cm；由此表明，隨著施工工況13～工況1進行，邊、中跨主纜位移幾何特性均依次經歷了幾何非線性特性增強、幾何非線性特性弱化、線性特性增強3個階段。

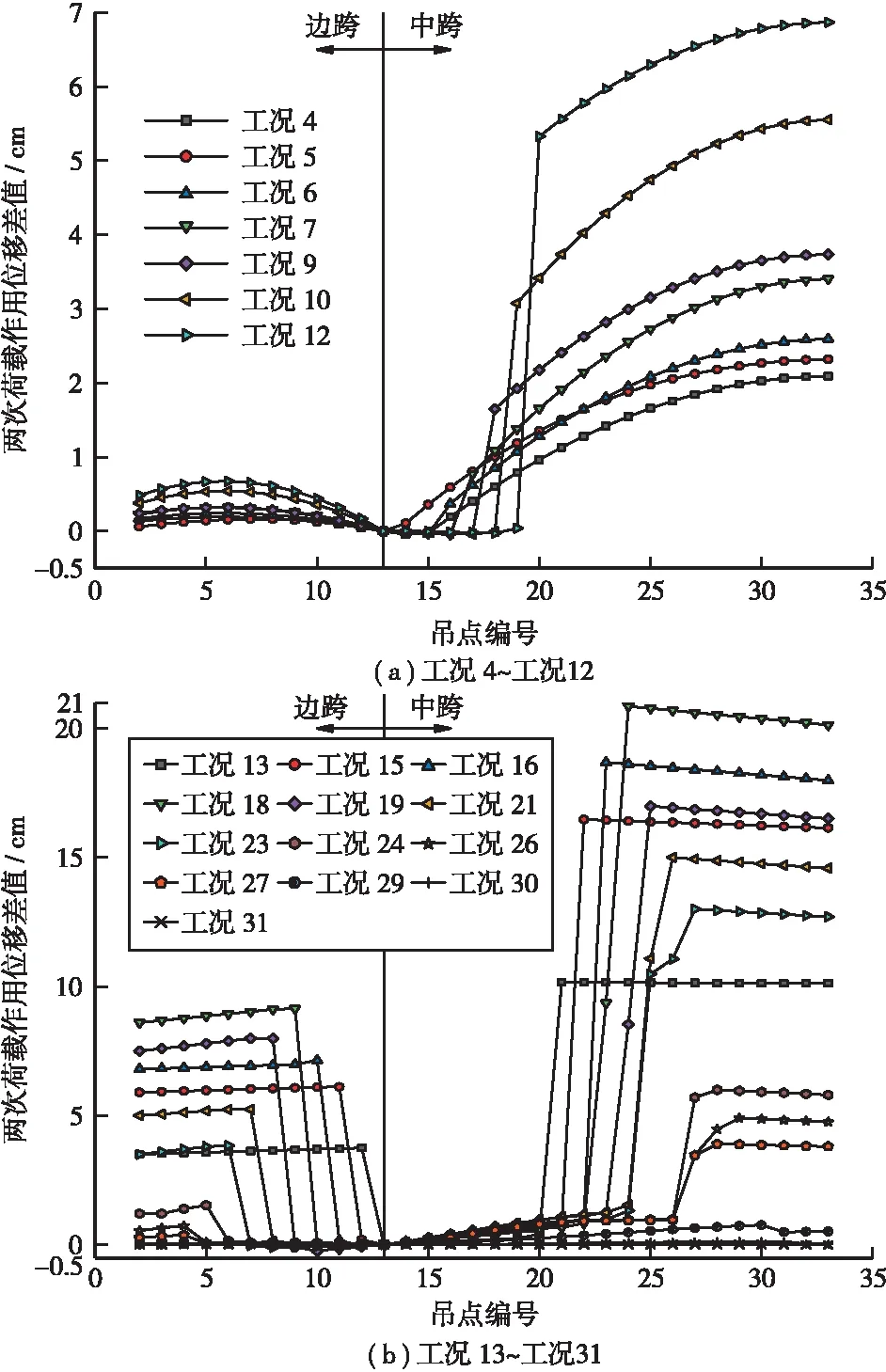
圖5 吊索張拉過程中主纜幾何非線性特征圖(單位：cm)

3.2.2臨時斜拉索拆除過程中主纜幾何非線性行為表現

采用分次加載法，在吊索張拉完畢后，將臨時斜拉索殘留的索力等分成2份，歷經連續兩次卸載將其拆除。通過數值模擬分析得到在臨時斜拉索拆除過程中主纜幾何非線性隨施工工序的行為表征如圖6。

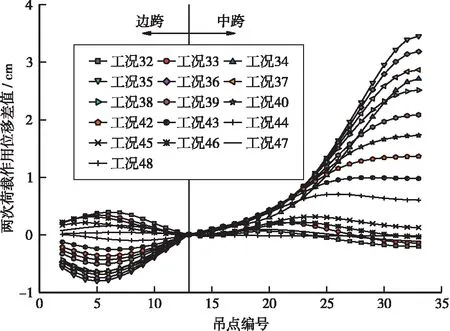
圖6 斜拉索拆除過程中主纜幾何非線性特征圖(單位：cm)

從圖6可知，在連續兩次卸載作用下，主纜豎向位移差值的最大值隨施工工況的歷程為：0.7 cm→3.5 cm→0，這表明了在臨時斜拉索拆除過程中主纜的幾何非線性呈現出“先由弱到強，再從強變弱”的變化規律，但主纜豎向位移差值的量程較小，且“由弱到強”僅持續了3個工況，因此在臨時拉索拆除過程中主纜的幾何位移特性以線性為主。

3.2.3主索鞍頂推作用下主纜幾何非線性行為表現

為了明確了解在主索鞍頂推作用下主纜的幾何非線性行為表現，將各頂推量均分成兩份，連續兩次作用得到各吊點位移差值隨頂推工況的變化曲線如圖7所示。

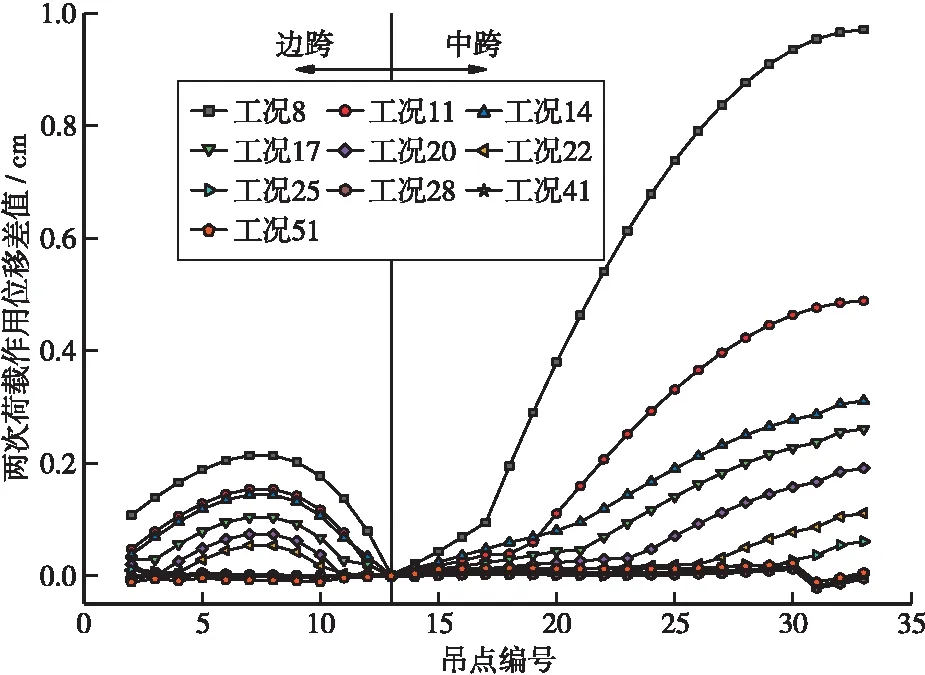
圖7 頂推工況作用下主纜幾何非線性特征圖(單位：cm)

分析圖7可知，在主索鞍頂推工況中，通過兩次連續相同作用，主纜的位移差值波動范圍基本在0～1.0 cm之間，這說明了在主索鞍頂推作用下，主纜位移特性呈現出顯著的線形特征。從圖中曲線變化趨勢可以看出，在主索鞍初始作用到最后一次頂推過程中，主纜的位移差值曲線基本表現出依次下降的變化規律，表明了主纜位移的線形特征在逐漸增強，這主要是由于隨著吊索的張拉和臨時斜拉索的拆除，主纜的重力剛度漸漸增大，豎向變形增量減小，主纜位移幾何非線性特性淡化，線性特性增強。

3.2.4成橋狀態下主纜的幾何非線性行為表現

為了研究主跨為600 m的超大跨自錨式懸索橋在成橋后主纜的幾何非線性行為表現，采用分次加載法，將二期恒載等分為兩份，連續兩次作用于結構，得到主纜在兩次作用下的變形差值見圖8。

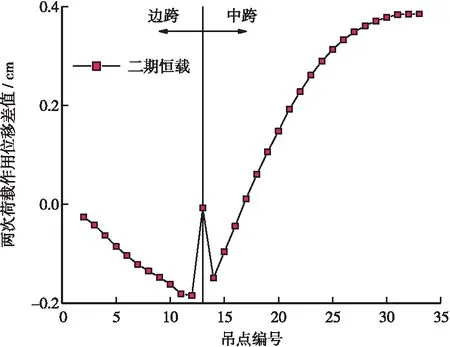
圖8 二期恒載作用下主纜幾何非線性特征圖(單位：cm)

從圖8可看出，將二期恒載均分成2份，連續兩次作用在主梁上，得到主纜在兩次作用下的豎向位移增量，二者差值的變動范圍在-0.2～0.4 cm，表明了超大跨自錨式懸索橋成橋后在恒載作用下主纜的位移表現為強烈的線形特性。

4 結論

以鵝公巖軌道專用橋為依托，探討了大跨自錨式懸索橋“斜拉-懸索”體系轉換過程中主纜的位移特性，得出以下主要結論：

a.主索鞍頂推使兩主索鞍之間的水平距離減小，即頂推使中跨主纜的水平投影距離減小，中跨主纜呈現出“松弛”狀態；邊跨主纜水平投影距離增大，邊跨主纜呈現出“緊繃”現象。邊、中跨主纜位移是主索鞍頂推作用和吊索張拉作用的總效應。

b.在吊索張拉階段，主纜位移特性主要經歷了線性特征顯著、幾何非線性特征增強、幾何非線性特征弱化3個階段。在體系轉換過程中，中跨主纜位移的幾何非線性特性比邊跨更加強烈。

c.在拆除臨時斜拉索階段，主纜的幾何非線性呈現出“先由弱到強，再從強變弱”的變化規律。

d.在主索鞍頂推及成橋恒載作用下，邊中跨主纜位移呈現出了顯著的線性特征，此時線彈性疊加原理適用。