基于蝙蝠算法的概率積分預計參數反演方法

李 忠，王 磊，滕超群，李世保，黃金中

(安徽理工大學空間信息與測繪工程學院，安徽 淮南 232001)

我國作為世界能源生產大國和消費大國，煤炭資源豐富，儲量居世界前列。作為三大化石燃料之一，煤是重要的能源，也是冶金、化學工業的重要原料，然而隨著大量煤炭資源的開采，常常引起開采區地層發生錯動、地表下沉等一系列問題，對礦區周圍村莊村民的生產生活產生了極大影響，因此開采沉陷預測的準確性顯得尤其重要[1]。概率積分法(probability integral method，PIM)預計模型是我國在開采沉陷中應用最廣泛的方法[2]，其參數反演過程經歷了線性近似法[3]、正交實驗法、模矢法[4]、人工神經網絡法[5]、智能優化算法(如遺傳算法[6])等。常見參數反演方法主要特點見表1。

表1 常見參數反演方法對比

目前遺傳算法在參數反演方面得到廣泛應用，國內很多學者利用智能優化算法進行概率積分法參數反演，如利用果蠅算法[7]、粒子群算法[8]、狼群算法[9]、混合蛙跳算法[10]等進行概率積分法模型參數反演，為概率積分法參數求解提供了眾多新的途徑。2010年YANG[11]提出了一種基于迭代優化技術的新型群體智能優化算法——蝙蝠算法(bat algorithm，BA)，因模型簡單易懂、參數少、求參穩定性高、收斂速度快等優點，現已在工程優化[12]、模型識別[13]等問題中得到了廣泛的應用，然而蝙蝠算法作為智能優化算法領域新的研究熱點，在概率積分模型參數反演的問題上卻鮮少有結合應用。

因此，本文將BA引入概率積分模型參數反演中，構建了基于蝙蝠算法的概率積分預計參數反演模型，并通過模擬實驗驗證蝙蝠算法反演模型的正確性，隨后將其應用于淮南市某煤礦1414工作面[14]的預計參數反演中，求得該工作面開采后沉降穩定時的預計參數。

1 模型構建

1.1 PIM基礎理論

按概率積分法原理，單元開采引起的地表任一點的下沉值計算見式(1)～式(4)。

W(x,y)=

(1)

W0=mqcosα

(2)

W0(x)=

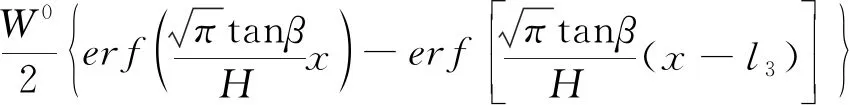
(3)

W0(y)=

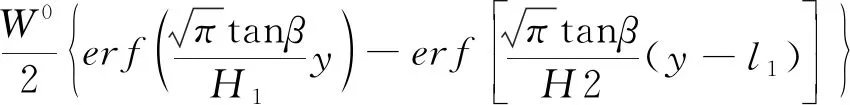
(4)

式中：m為工作面平均開采厚度；q為下沉系數；α為工作面傾角；tanβ為主要影響角正切；H為走向主斷面采深；H1、H2分別為工作面上邊界采深、下邊界采深；D3、D1分別為開采工作面走向長度、傾向長度；l3、l1分別為工作面走向計算長度、傾向計算長度。

同理，單元開采引起的地表任一點沿φ方向的水平移動值計算見式(5)～式(7)。

U(x,y,φ)=

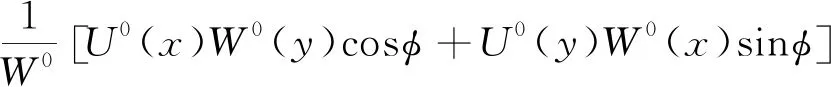
(5)

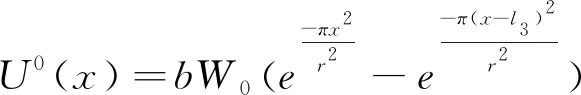
(6)

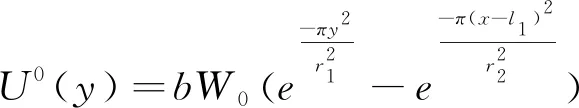
(7)

式中：b為水平移動系數；φ為x軸的正向逆時針到指定方向的角值；r1、r2為下山主要影響半徑和上山主要影響半徑。

1.2 BA基礎理論

蝙蝠可以在夜間自由飛翔并準確無誤地捕捉食物，主要是依靠它們的喉頭發出超聲脈沖進行回聲定位，在蝙蝠算法中，為了模擬蝙蝠捕食獵物、避免障礙隨機搜索過程，做出三種近似理想化規則假設。

1) 在設定的種群里，所有的蝙蝠獲取方法和距離的方法都是回聲定位。

2) 蝙蝠i在某一位置X時以Vi的速度進行飛行，其具有固定的頻率fmin，并且可以利用自身與目標的距離自動調整脈沖響度A和波長λ。

3) 設定脈沖響度A是一個由最大值A0變化到固定最小值Amin的過程，具體的A0和Amin的值由所解決的問題而調整。

fi=fmin+(fmax-fmin)×β

(8)

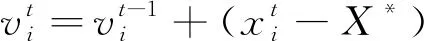
(9)

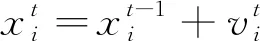
(10)

式中：fi為蝙蝠發出聲波的頻率，其變化在[fmin，fmax]的區間范圍內，在具體問題中根據問題的需要設置對應的頻率變化范圍；β為屬于[0,1]的隨機向量；X*為當前群體中局部最優解位置。

在進行局部搜索時，若生成了一個局部新解，則新的局部解將會采用的生成方式為隨機游走，新的局部解生成規則為式(11)。

xnew=xold+ε×At

(11)

式中：ε為一個[-1,1]范圍內的隨機數；At為整個群體里同一代的平均響度。

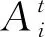
(12)

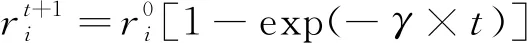
(13)

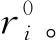
1.3 BA-PIM模型構建

假設在工作面任意一點(x,y)進行開采，Wxy為開采點的實際下沉值，Uxy為開采點的實際水平移動值，將BA反演的PIM預計參數帶入到PIM模型中，得到開采點的預計下沉值及水平移動值Wxy預和Uxy預,并構造以開采點的實測值與預計值之差的絕對值累計和最小為標準的適應度函數見式(14)。

S=sum[abs(Wxy-Wxy預)+abs(Uxy-Uxy預)]

(14)

令X*=[q，tanβ，b，θ，S1，S2，S3，S4]為BA算法中最優蝙蝠位置的解空間，將適應度函數值最小作為判斷每一次蝙蝠最優位置的標準。在每一次迭代的過程中蝙蝠群體根據調整脈沖響度和頻率來搜尋并捕獲獵物，當滿足終止條件后，輸出最優的蝙蝠位置X*。其算法模型的具體步驟如下所述。

1) 設置蝙蝠群體的數量N，最大迭代次數T，蝙蝠聲波頻率范圍值[fmin，fmax]，蝙蝠i的初始速度V、脈沖響度衰減系數α及脈沖頻度增強系數γ的大小、初始脈沖大小；約束PIM八參數的波動范圍，讀取觀測點的實際下沉值Wxy和水平移動值Uxy。

2) 機初始化蝙蝠Xi的位置并利用式(14)中的適應度函數輸出最優的蝙蝠位置并儲存。 由式(8)～式(10)更新蝙蝠i此時的頻率、速度及位置。

3) 生成一個[0,1]隨機數Rand1，如果Rand1大于當前最優蝙蝠發出的脈沖頻率ri則根據式(11)進行局部新解搜尋并儲存當前新解，否則繼續利用式(10)更新蝙蝠的位置。

4) 繼續生成一個[0,1]隨機數Rand2，如果Rand2小于當前最優蝙蝠發出的脈沖響度Ai，并且此時適應度函數生成的解優于步驟3)的解，則接受此時蝙蝠的最新位置解，然后根據式(12)和式(13)更新蝙蝠i的脈沖響度和頻率。

5) 對種群中所有蝙蝠個體的適應度值進行排序，輸出當前最佳位置蝙蝠。

6) 轉到步驟2)～步驟5)，直到達到迭代次數，輸出全局最優蝙蝠位置X*。

基于BA的概率積分預計參數反演方法程序流程圖如圖1所示。

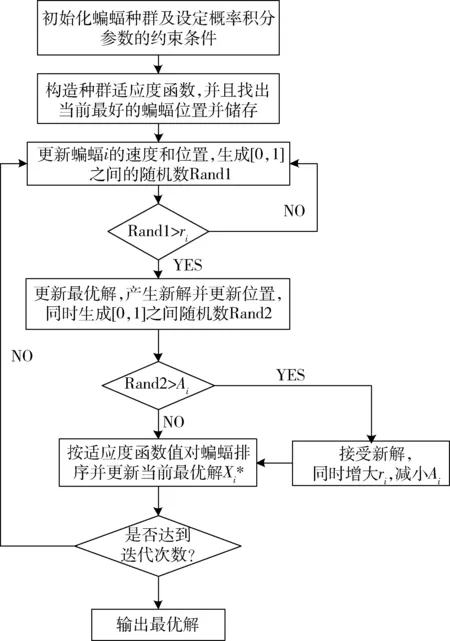
圖1 BA反演PIM參數流程圖

2 模擬實驗

2.1 工作面概述

為了驗證BA算法應用于PIM求參的準確性，故建立如下模擬工作面：矩形工作面走向長度D3=600 m，傾向長度D1=300 m，煤層開采厚度m=3.6 m，煤層傾角α=6°，平均開采深度H=400 m，管理頂板的方法采用全部垮落法。此次模擬工作面實驗走向主斷面上相鄰兩個觀測站之間間隔30 m，傾向主斷面觀測站布設方式同走向。假定模擬工作面PIM預計參數分別為：下沉系數q=0.9，主要影響正切角tanβ=2.1，水平移動系數b=0.35，開采影響傳播角θ=87°，拐點偏移距：S1=S2=50 m、S3=S4=50 m。本模擬工作面設計圖如圖2所示。

圖2 模擬工作面設計圖

2.2 BA參數反演準確性分析

智能算法在一定范圍內具有隨機性，為避免偶然誤差對實驗結果準確性的影響，在相同的實驗環境下連續進行了10次BA參數反演實驗。設置初始蝙蝠種群個數為400，最大迭代次數為100。以BA進行概率積分參數反演， 并將模擬實驗參數預設值與BA參數反演值進行對比分析，通過反演參數中誤差和相對誤差來反映BA反演參數的準確性，實驗結果見表2。

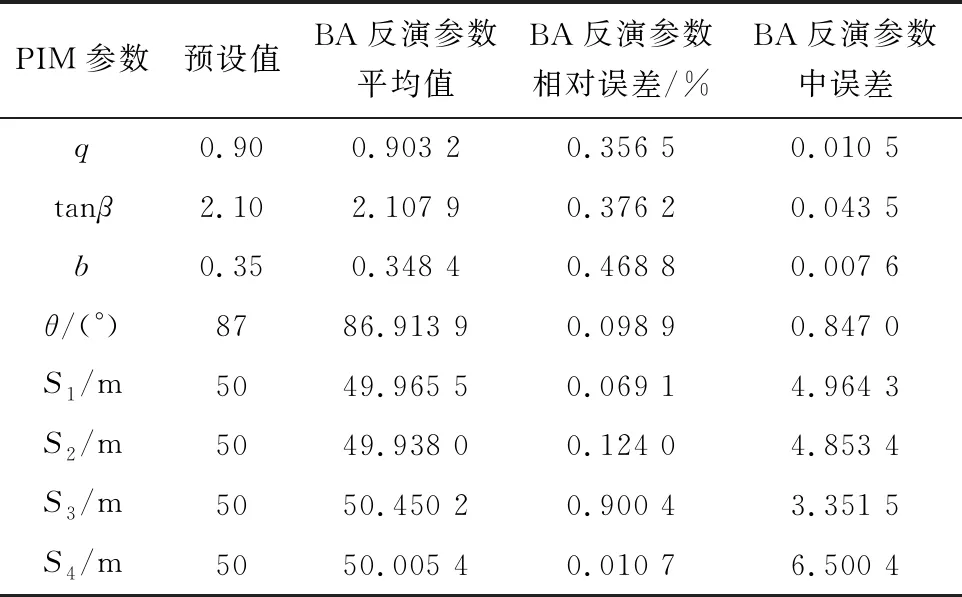
表2 BA反演參數值與預設值對比

由表2可知，BA反演參數相對誤差方面，S1、S2、S3、S4、q、tanβ、b、θ反演準確性較高，相對誤差均不超過1%，且在中誤差方面，S1、S2、S3、S4的中誤差均不超過7 m，q、tanβ、b、θ反演準確性較高，中誤差均不超過1。由此可見BA反演PIM參數具有較高的準確性。

為了更好地分析BA算法的準確性，需要對下沉和水平移動的擬合情況進行分析，故通過10次BA參數反演實驗取PIM參數均值，計算模擬工作面的下沉與水平移動值，具體曲線如圖3和圖4所示。由圖3和圖4可知，通過BA反演的PIM參數計算的下沉值和水平移動值擬合效果良好，達到預期精度，故BA參數反演準確度較高。

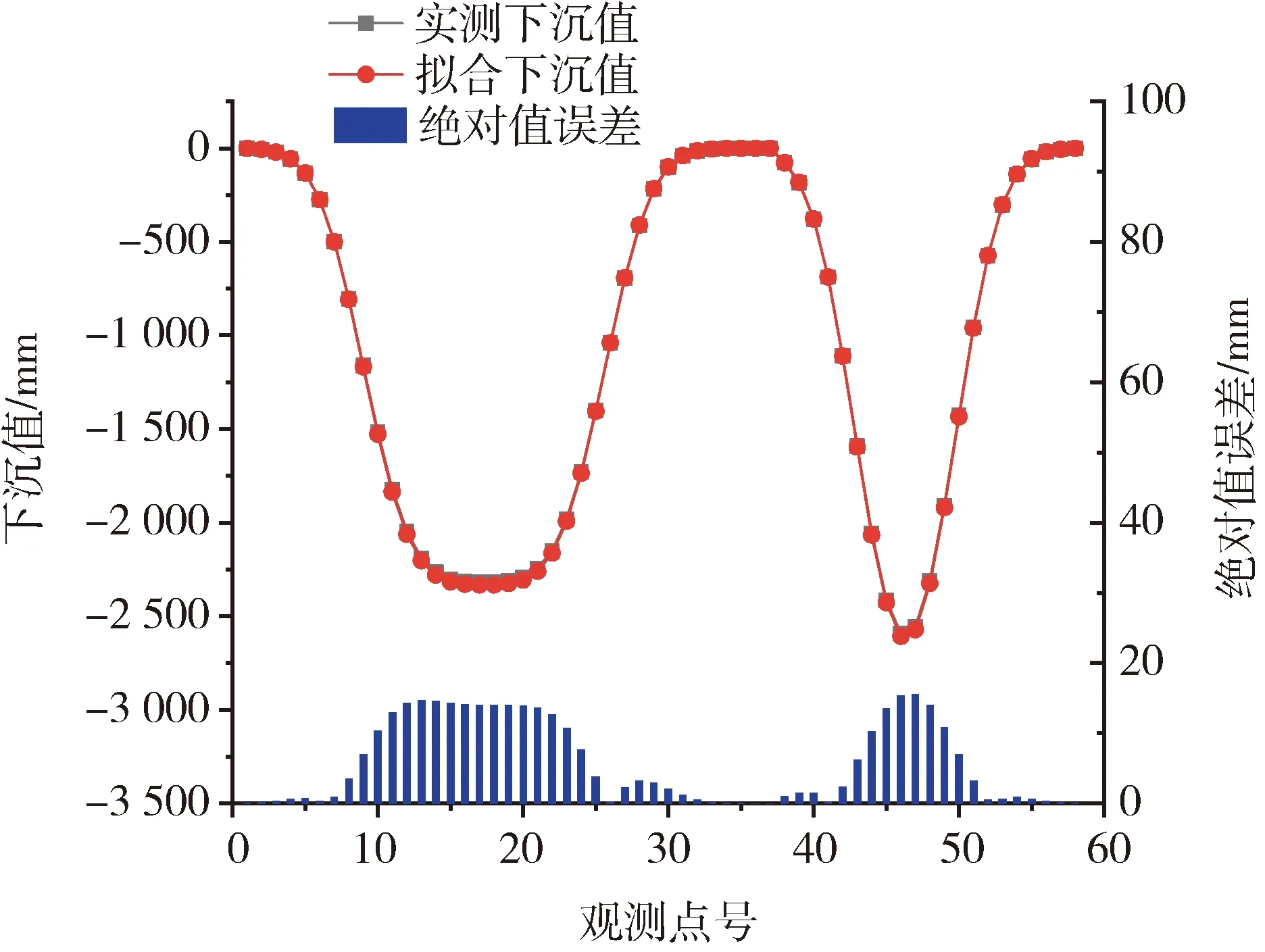
圖3 BA模擬實驗擬合下沉值與實測下沉值對比圖

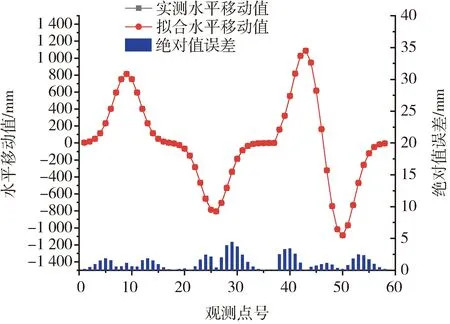
圖4 BA模擬實驗擬合水平移動值與實測水平移動值對比圖

2.3 BA參數反演波動性及抗隨機誤差分析

為了進一步驗證BA參數反演的穩定性，對模擬實驗反演10次的PIM參數分別進行波動性分析，結果如圖5所示。由圖5可知，通過BA反演的PIM參數在真值附近波動范圍較小，具有較好的穩定性。

圖5 模擬實驗10次反演參數的波動情況

為進一步驗證BA在反演PIM參數時是否對隨機誤差具有一定的抗干擾能力[15]，將模擬實驗走向線和傾向線上共58個監測點的下沉值隨機地先后減少5 mm、10 mm、15 mm，水平移動值隨機地先后減少2 mm、4 mm、6 mm，再用三組具有隨機誤差的模擬監測數據通過BA進行10次PIM參數反演，最后與預設參數進行對比分析，結果見表3。由表3可知，在隨機加入誤差后，BA反演PIM參數仍具有較好的穩定性，說明BA反演PIM參數模型具有一定的抗隨機誤差干擾能力[16]。

表3 BA反演PIM參數模型抗隨機誤差分析

3 工程實例

結合安徽省淮南市某煤礦1414工作面地表觀測站[14]實測的下沉值和水平移動值對BA反演PIM參數方法進行分析，該工作面走向長度為2 120 m，傾向長度為251 m，工作面平均深度為735 m，煤層平均傾角為5°，平均采高為3.0 m。選取該工作面走向線上75個監測點，傾向線上47個監測點共122個監測點的實測數據為基礎，利用BA反演10次PIM參數求取均值的方法計算預測的下沉和水平移動值并與監測點的下沉和水平移動值進行對比分析，并計算BA反演10次參數的平均值與中誤差。其結果見表4。

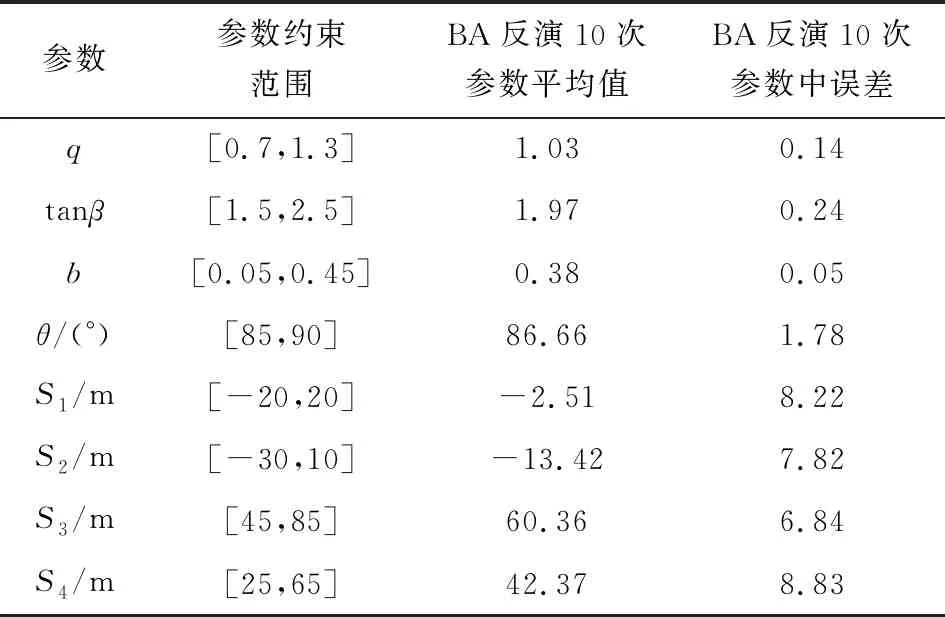
表4 BA反演參數工程實例結果

由圖6和圖7可知，擬合下沉值和水平移動值曲線與實測曲線基本一致，監測點的擬合值與實測值之間的絕對值誤差均在250 mm范圍以內，而且BA反演10次PIM參數取平均值后，其下沉值與水平移動值的擬合中誤差為116.34 mm。一般認為對下沉來說，擬合中誤差小于最大下沉值的5%；對水平移動來說，擬合中誤差小于最大水平移動值的10%；而本文所求的下沉值擬合中誤差約為最大下沉值的3.5%，水平移動值擬合的中誤差約為最大水平移動值的1.49%。滿足上述條件，符合工程應用標準[17]。

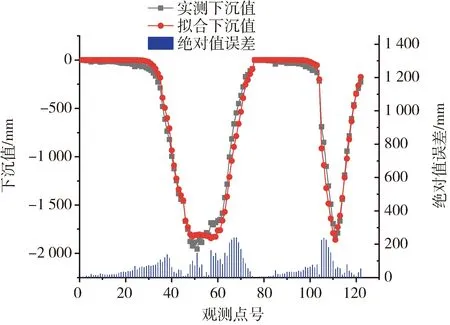
圖6 BA擬合下沉值與實測下沉值對比圖

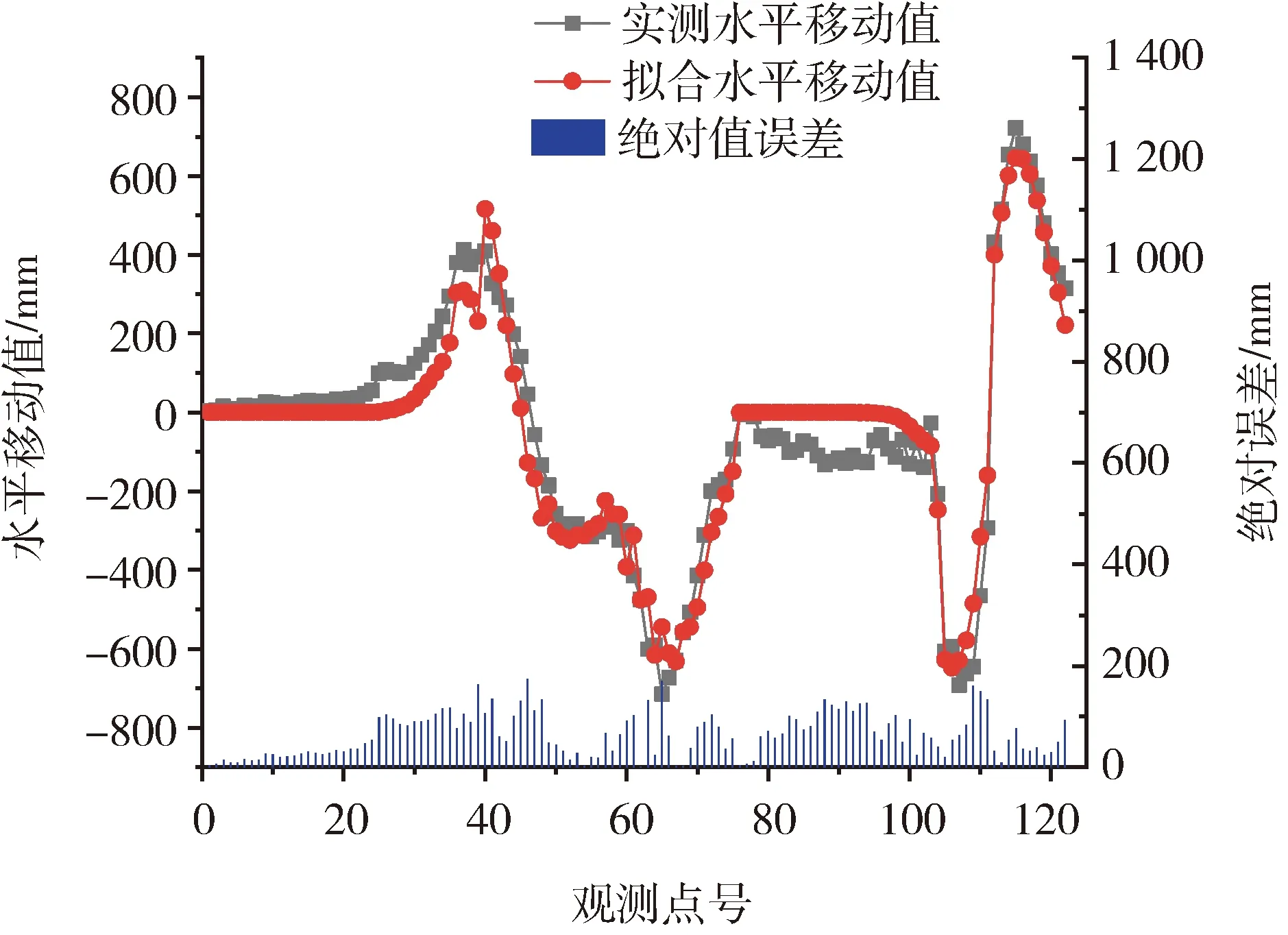
圖7 BA擬合水平移動值與實測水平移動值對比圖

4 結 論

1) 模擬實驗：各預計參數q、tanβ、b、θ、S1、S2、S3、S4、反演相對誤差均不超過1%且q、tanβ、b、θ反演中誤差均不超過1，S1、S2、S3、S4反演中誤差均不超過7 m；模擬實驗驗證了基于BA的概率積分參數反演模型的可靠性與準確性。

2) 工程實例：將BA算法應用于淮南市某煤礦的預計參數反演中，求解的預計參數分別為：q=1.03、tanβ=1.97、b=0.38、θ=86.66°、S1=-2.51 m、S2=-13.42 m、S3=60.36 m、S4=42.37 m，下沉及水平移動擬合中誤差為116.34 mm，符合工程應用標準。

3) 在進行PIM參數求解時，BA算法原理簡單、參數較少且易于編程實現等優勢，對于附近礦區精準PIM參數反演具有一定的參考價值。