G-KSVD字典及其在滾動軸承故障信號稀疏表示中的應用

孟 宗 郜文清 潘作舟 張光雅 樊鳳杰

燕山大學電氣工程學院，秦皇島，066004

0 引言

滾動軸承作為旋轉機械的關鍵部件，其運行狀態直接影響旋轉機械設備的安全可靠運行[1-2]，因此，對滾動軸承進行故障診斷具有重要意義[3-4]。在滾動軸承診斷故障中，振動信號分析方法是最常用的方法之一。依據傳統的香農采樣定理對滾動軸承振動信號采樣時會產生大量數據，從而加大了信號后續分析處理的難度。近年來，隨著稀疏表示的出現，基于稀疏表示的滾動軸承信號分析方法使數據量得到有效降低，信號處理難度也得以減小。

稀疏表示包含字典設計與稀疏編碼兩個部分[5-6]。在假定字典已知的前提下，利用稀疏編碼能夠求解出表示輸入信號的稀疏向量，因此，字典是稀疏表示的關鍵，它主要分為分析字典和學習字典兩類。分析字典能夠利用固定的函數基直接得到字典[7]，在提取信號中的沖擊成分、簡諧振動及其他瞬態現象方面較為直接有效。然而隨著信號的變化，基函數也要隨之變化，由此使得信號分析的難度增加，在具體的應用中普適性不高。不同于分析字典，學習字典是從數據中訓練得到的字典，具有更好的稀疏度和重構精確度[8-9]。目前，相關學者已經針對學習字典提出了一系列壓縮信號的方法，用以解決復雜信號難以處理的問題。AHARON 等[10]基于K-means聚類思想，首次提出了K-奇異值分解(K-SVD)算法。YANG等[11]針對相同模式下周期性出現的長信號，提出了一種基于移位不變字典學習的故障診斷法。LIN等[12]針對K-SVD算法在故障信號較長時引起的時間成本增加的問題，提出了以小段含沖擊時域信號進行滑動窗口字典學習的新式去噪K-SVD方法。樂友喜等[13]提出一種完備總體經驗模態分解與K-SVD學習字典算法相結合的地震信號去噪方法。QIN等[14]提出了一種基于自適應火花停止準則的OMP算法，進而提出了一種新的K-SVD信號矩陣和初始瞬態字典的構造方法。SHAO等[15]針對標簽一致K-SVD算法，在正則化1字典學習算法中應用標簽信息，提出了標簽嵌入字典學習方法。然而，上述有關K-SVD的算法中，由于缺少對原子相干性的分析，降低了重構信號與原始信號所含故障信息的相似度，從而導致故障診斷準確度的下降。奇異值分解[16]作為K-SVD訓練字典過程中的關鍵環節，具有優良的數值穩健性。ZHAO等[17]提出能夠描述復雜信號奇異值突變狀態的奇異值差分譜，用來實現有效奇異值的自動選取。REZA等[18]利用奇異值分解和Hankel矩陣實現了對滾動軸承時域振動信號及其頻譜的去噪處理。LI等[19]針對早期微弱故障信號，提出了一種基于SVD和OFBE的滾動軸承故障特征提取方法，利用SVD實現了信號降噪。ZHU等[20]結合BCS和嵌入式SVD提出一種圖像加密方案，以此來增強方案的魯棒性。由上述文獻可知，奇異值分解能夠提高信號處理的精度，同時奇異值的選取關系到奇異值分解的降噪效果，然而在訓練字典中缺少合適的指標來選取有效的奇異分量，從而導致重構信號信噪比的下降。

在對學習字典進行訓練的過程中，針對奇異分量之間的相干性，本文提出了一種基于自相關函數脈沖能量比(auto-correlation function pulse energy ratio，ACFPER)的G-K奇異值分解(G-KSVD)訓練字典。ACFPER指標能夠優化奇異分量的選擇，獲取最優原子；結合最優原子的學習字典算法能夠在減小噪聲的同時，增強沖擊信號；G-KSVD算法在迭代更新中由于反饋的減少，可降低算法的時間成本。

1 K-SVD學習字典

在信號稀疏表示的過程中，K-SVD算法是目前應用最廣的字典學習方法，其核心思想是對字典原子進行逐列更新，目標函數為

(1)

其中，Y是由原始信號構成的訓練樣本，D是學習字典，‖·‖F是lF范數，xi是系數矩陣X的第i列向量，T0是稀疏度。K-SVD算法首先通過固定字典D，利用OMP算法對稀疏系數X進行更新，然后通過優化問題對字典進行逐列更新。更新原子的誤差矩陣El的計算公式[9]如下：

(2)

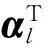
(3)

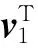
2 基于G-KSVD學習字典的信號重構

2.1 信號預處理

軸承信號在進行稀疏表示及壓縮重構的過程中，對信號進行一定的預處理，能夠降低信號在稀疏表示過程中的難度。本文在對實際信號預處理時主要考慮以下兩個問題：一是通過傳感器采集到的軸承信號通常是包含噪聲的，這增加了數據處理等的難度；二是數據的偶然性、單一性會給實驗結果帶來一定的誤差，需要通過多次實驗驗證。

在實驗過程中，需要對所提方法的有效性進行判斷。然而，實驗采集到的軸承信號長度較大，導致單次完整實驗所消耗的時間過長，無法及時有效地讀取信號特征量。因此，本文在獲取到軸承信號之后，對信號進行分段處理[21]，并對分段后的信號進行壓縮重構，減少信號的冗雜度。對軸承信號的分段過程如下：

(1)確定信號總長度N、信號的段數φ，每段信號的長度n，則三者關系為

N=φn

(4)

記第φ段信號為sφ，則原始信號s可表示為

s=[s1s2…sφ…sφ]

(5)

(2)利用G-KSVD算法從信號sφ中訓練出稀疏字典Dφ，則

(6)

以字典D作為先驗條件對信號進行重構，得

(7)

記錄每段信號的特征量。

(4)對信號進行降維整合，得到重構信號：

x=[x1x2…xφ…xφ]

(8)

2.2 自相關函數脈沖能量比

特征分量的有效識別有利于對故障信號中的脈沖序列進行準確提取[22-23]。基于此，本文針對敏感原子對故障信號檢測中精度的影響，提出自相關函數脈沖能量比，并以此為標準篩選敏感原子，識別有效的特征分量。

在時域中，相關函數[24]是信號相關性的平均度量，本文根據相似度這一特性，利用相關函數對信號進行處理，選用的相關函數分別為互相關函數和自相關函數，并根據實驗結果來選擇較優的相關函數。通過實驗發現，自相關函數可以更加準確地檢測出脈沖序列。噪聲信號的自相關函數集中分布在零點處，原信號的自相關函數則能夠較好地保留脈沖信號的周期[25]，因此，對信號進行自相關處理能夠減少噪聲對沖擊脈沖的影響。由于信號幅值以及窗口長度的作用，信號的自相關函數在傳統的算法中會出現其首個極值點估值起伏較大的問題。為改善這一情況，本文采用歸一自相關函數R(t)對含噪信號進行處理：

(9)

其中，n0表示信號的窗口長度，x(t+i)表示在t+i時段內截取的信號，τ表示時間延遲，δ為信號標準差。對信號進行自相關歸一化后，信號的最大幅值為1，能夠減小歸一化前信號的幅值波動，增強信號的魯棒性。

為了計算信號的歸一自相關函數及N的長度，對測量信號進行Hilbert變換得到包絡信號s(t)，并對信號進行去直流處理后得到信號l(t)：

y(t)=|s(t)|

(10)

(11)

(12)

Teager能量算子[26-27]能夠測量單個時變信號在機械過程中產生的能量，具有較高的時間分辨率，并且能自適應地檢測信號的瞬時變化。Teager能量值通過跟蹤信號的瞬時能量能夠檢測信號的沖擊脈沖，為信號分析提供了新的途徑。對于離散信號x(n)，其能量算子的定義為

φ[x(n)]=[x(n)]2-x(n-1)x(n+1)

(13)

Teager能量信號包含由脈沖故障特征引起的幅度調制和頻率調制的信息。Teager能量算子在提高沖擊信號信噪比和表述信號特征方面具有很大優勢。基于此，本文提出了自相關函數脈沖能量比(ACFPER)RAC：

(14)

2.3 G-KSVD學習字典

為了提高傳統的K-SVD學習字典的精度，在字典更新階段，G-KSVD算法以ACFPER為指標選取含有沖擊脈沖的敏感原子，通過歸一自相關函數對信號進行降噪，再由Teager能量算子追蹤信號的瞬時能量，使更新的字典原子中包含更多的故障信息，從而提升故障信息識別過程中的準確率。

傳統的K-SVD學習字典算法中，在對系數矩陣列向量以及字典原子進行更新的過程中，會再次調用對誤差矩陣進行奇異值分解相關的函數，考慮到時間因素對故障診斷效率的影響，本文在確定敏感原子后，通過對字典原子進行直接賦值、歸一化處理，減少反饋過程的處理，降低算法的時間成本。算法的具體步驟如下：

(1)選取訓練樣本信號Y，確定初始字典原子長度N，稀疏度K，算法迭代次數J。根據信號Y構造初始字典。

(2)利用OMP算法對數據進行稀疏表示，獲得信號在當前字典下的稀疏系數矩陣X。

(3)固定系數矩陣X，對X中每列元素αi進行賦值，開始迭代。

(4)根據式(2)計算出誤差矩陣Ei，并確定αi中非零項的位置索引集合Ωi。

(6)對矩陣U中每個原子uj求取ACFPER值，得到特征量ACFPER最大時對應的原子uj，并用其來更新字典單元。

(7)為了減小奇異分量間差異對系數矩陣更新、重構信號精度的影響，確定矩陣中最接近均值的奇異分量的位置索引ε。

(8)利用索引對系數矩陣X中的列元素進行更新：

(15)

(9)利用(6)中所得原子uj對第i列字典元素di進行賦值及歸一化處理。

(10)迭代停止后，輸出字典D和稀疏系數矩陣X，進行二次重構。

3 仿真實驗

為驗證本文算法的降噪效果，針對振動信號的特點，構造以下仿真信號進行實驗：

(16)

本文中參數設置如下：As=0.01，f=200，z=0.05，周期T=0.1 s，采樣頻率fs=1000 Hz。在信號y中加入不同噪聲強度的高斯白噪聲n，以模擬不同噪聲環境下采集到的信號。此處以0 dBW的高斯白噪聲為例，繪制圖1所示信號，并計算3種信號的歸一自相關函數，結果如圖2所示。

從圖1、圖2可以看出，周期脈沖信號的歸一自相關函數能夠較好地保留信號周期；噪聲信號的歸一自相關函數集中在零點附近，即在零點處幅值較大，在非零點處幅值接近0；混合信號的歸一自相關函數在零點處幅值較大，在非零點處的脈沖周期與原始信號相同。由此可以看出，歸一自相關函數能夠在降低信號中噪聲成分的同時，保留信號脈沖。因此，基于ACFPER改進的G-KSVD算法能夠達到降低噪聲信號的目的。

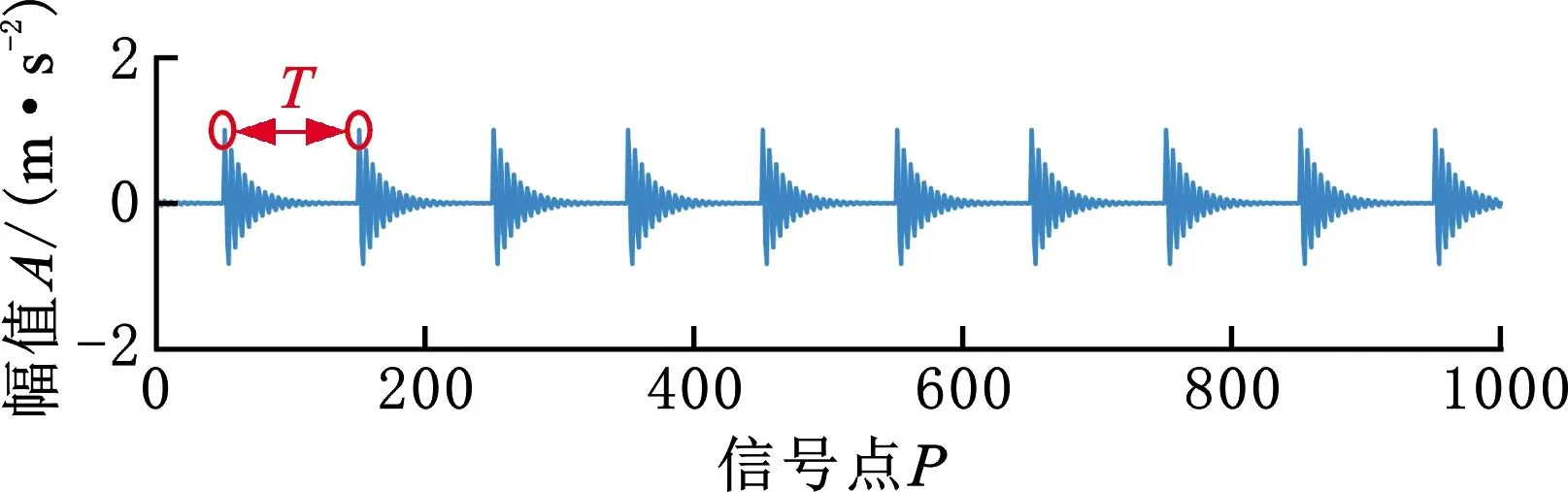
(a)脈沖信號

(a)脈沖信號

為了進一步驗證G-KSVD算法的降噪效果，利用G-KSVD算法對字典原子進行特征量的學習以得到新的稀疏字典，再通過測量矩陣對信號進行重構，分析重構信號的特征量。因所加噪聲強度的不同，字典學習的效果不同，重構所得的信號精度也有差異。本文對所提方法的適用范圍進行驗證，判斷G-KSVD算法的應用效果及區間。由于實驗信號的采集會受到各種不定性因素的影響，無法衡量確切的噪聲強度，故本文通過仿真信號模擬不同強度的噪聲環境，并對同一噪聲環境下的G-KSVD算法及K-SVD算法進行驗證和對比，來判斷兩者的去噪效果。

在信號處理過程中，為了衡量處理后信號中的噪聲含量，引入信噪比這一概念。信號強度PS與噪聲PN的比值定義為信噪比(signal-to-noise ratio，SNR)：

RSN=10lg(PS/PN)

(17)

由上式可知，噪聲的功率越小，信噪比越大，同理，噪聲的功率越大，信噪比越小。為驗證本文方法的應用環境以及兩種算法的有效性，分別對加入不同強度噪聲的信號進行G-KSVD字典學習和K-SVD字典學習，利用信噪比衡量兩種方法的去噪效果。由于K-SVD算法在強噪聲環境下效果較差，故從0 dBW的噪聲環境開始，以-5 dBW和5 dBW為一個單位長度，通過500次重復實驗后，對不同強度噪聲環境下K-SVD算法和G-KSVD算法的有效性進行驗證，記錄實驗結果并求均值，見表1。

表1 不同噪聲環境下G-KSVD算法和K-SVD算法的信噪比

為了更清晰地對比以上兩種算法的有效性，確定G-KSVD算法的閾值，對表1中數據進行處理。將G-KSVD 信噪比RSN1與K-SVD 信噪比RSN2的差值定義為差值信噪比(DSNR)：

RDSN=RSN1-RSN2

(18)

當G-KSVD算法與K-SVD算法的差值信噪比大于零時，G-KSVD算法的去噪效果優于K-SVD算法的去噪效果。將不同強度噪聲下的差值信噪比繪入圖3。

圖3 G-KSVD算法與K-SVD算法的差值信噪比

由圖3可以看出，當噪聲強度在-10～35 dBW這一區間時，差值信噪比均大于零，說明G-KSVD算法在該區間的信噪比大于K-SVD算法的信噪比，即G-KSVD算法的去噪效果優于K-SVD算法。噪聲強度為-15 dBW和40 dBW時，差值信噪比小于零，說明G-KSVD算法在這兩點的信噪比小于K-SVD算法的信噪比，降噪效果有所下降。為了精確確定G-KSVD算法的應用區間，以1 dBW為一個單位長度對-15～-10 dBW及35～40 dBW兩個區間進行仿真實驗，記錄數據見表2、表3。同理，為了更直觀地觀察G-KSVD算法的適用環境，將兩個區間中G-KSVD算法和K-SVD算法的差值信噪比分別繪入圖4。

表2 G-KSVD算法和K-SVD算法的信噪比(-15～-10 dBW區間)

表3 G-KSVD算法和K-SVD算法的信噪比(35～40 dBW區間)

由圖4可以看出，在-15～-10 dBW區間內，-13～-10 dBW這一區間內的差值信噪比均大于零，而-15 dBW和-14 dBW的差值信噪比小于零，因此，G-KSVD算法應用環境的噪聲強度下限為-13 dBW。此外，在35～40 dBW區間內，35～38 dBW之間的差值信噪比均大于零，而39 dBW和40 dBW的差值信噪比小于零，由此可以確定G-KSVD算法所應用環境的噪聲強度上限為38 dBW。

(a)-15～-10 dBW區間的差值信噪比

綜合比較以上數據，G-KSVD算法的應用范圍為-13～38 dBW，即在這一區間內，同一噪聲強度下G-KSVD算法的去噪效果優于K-SVD算法的去噪效果，在故障診斷的過程中，G-KSVD算法能夠減少噪聲對沖擊序列的影響，更加準確地識別沖擊脈沖，對于故障特征的提取也更加準確。

4 實驗與分析

為進一步驗證本文算法對實際信號的應用效果，采用圖5所示燕山大學機械故障綜合模擬實驗臺的內圈數據進行實驗。實驗臺由兩個3/4英寸ER-12K轉子軸承組成。驅動系統中電機轉速n始終保持在1200 r/min，基頻fB=n/60=20 Hz。裝載系統由兩個轉子組成，轉子的厚度為15.9 mm，自重為6.5 N，直徑為151.3 mm。采集系統使用NI 9234加速采集卡，其頻率為12.8 kHz，軸承頻率為32 Hz，采集時間為64 s。為驗證本文所提的自相關函數脈沖能量比對有效特征分量的提取效果，對ACFPER中涉及到的函數進行驗證。由于振動信號的長度較大，為降低數據處理的壓力，對信號進行分段訓練，并計算每段信號的信噪比，最后根據信噪比的均值判斷信號的重構效果。為減小隨機性帶來的誤差，本文中實際實驗的結果是通過500次重復實驗后所求的均值。

圖5 機械故障綜合模擬實驗臺

4.1 構造ACFPER時相關函數的比較分析

為驗證本文所涉及的歸一自相關函數、自相關函數、互相關函數的去噪效果，以及與原信號的相似度，分別利用3種相關函數對信號進行降噪處理，結果如圖6所示。可以看出，信號的歸一自相關函數和自相關函數與原信號的相似度較高，保留了原始信號的沖擊序列周期，而信號的互相關函數只在2×104處有明顯脈沖，與原信號的相似度較低。觀察前兩個相關函數后發現，信號在零點處的幅值最大，且大于原始信號在零點處的脈沖序列，而在非零點處的幅值近似于原始信號的脈沖序列，說明前兩個相關函數有較好的降噪效果，且噪聲信號主要集中在零點附近。

(a)內圈故障信號

分別將歸一自相關函數、自相關函數以及互相關函數應用到ACFPER中，構造學習字典G-KSVD、G-KSVD1、G-KSVD2，通過3個不同的學習字典對數據進行訓練，得到的信噪比見表4。為了更加充分地描述本文算法的優越性，本實驗同時記錄了各學習字典的峰峰值，以此反映不同相關函數對應的信號幅值大小。

表4 不同相關函數對應學習字典訓練數據的特征量

由表4可以看出，G-KSVD學習字典的信噪比最大，G-KSVD1次之，G-KSVD2信噪比最小，所以，相比較其他兩種字典，G-KSVD的去噪效果更好，提取到的沖擊序列能夠包含更多的有用信息。就峰峰值而言，G-KSVD字典的值大于其他兩種字典，由此可以看出，通過G-KSVD學習字典重構的信號的幅值更大，能夠更準確地識別沖擊序列。

4.2 構造ACFPER時參數變化對信號稀疏表示的影響

噪聲信號的相關函數在零點處達到最大值，其能量主要集中分布在零點附近[26]。脈沖故障信號的相關函數則保留了脈沖周期，其能量基本不會受到影響。因此，脈沖故障和噪聲可以通過歸一自相關函數進行分離。

在式(14)中，ξ和k值的選取均會對學習字典的稀疏效果產生影響。由于噪聲信號的歸一自相關函數在第一個極值點處的能量較為集中，故當ξ=2時，學習字典能達到更好的去噪效果，為了驗證這一結論，分別取ξ=1、ξ=2和ξ=3進行實驗。同理，對k的取值進行驗證，文獻[24]中建議k=3，因此，本文對k=3附近的取值進行驗證，其中，信號的信噪比見表5。除此之外，將通過不同字典壓縮重構的信號峰峰值記錄于表6。

表5 不同ξ值和k值對應學習字典訓練數據的信噪比

表6 不同ξ值和k值對應學習字典訓練數據的峰峰值

由表5可以看出，ξ=1時，信噪比在k=3時達到最大值1.0805 dB；ξ=2時，信噪比在k=3時達到最大值1.1096 dB；ξ=3時，信噪比在k=4時達到最大值1.0742 dB。對比這3個數據發現，當ξ=2及k=3時，信噪比達到最大值，說明此時GSKVD的去噪效果最好，精度更高，噪聲信號對沖擊序列的影響最小。

由表6可以看出，ξ=1時，峰峰值在k=2時達到最大值0.6894 m/s2；ξ=2時，峰峰值在k=3時達到最大值0.6944 m/s2；ξ=3時，峰峰值在k=4時達到最大值0.6864 m/s2。對比這3個數據發現，當ξ=2及k=3時，峰峰值最大，說明沖擊信號的幅值更大，有利于后期的故障提取。

綜上，當ξ=2及k=3時，G-KSVD學習字典取得的效果較優。對比信噪比后發現，G-KSVD算法在對故障信號壓縮重構的過程中能夠有效地降低信號中的噪聲成分，從而達到降噪的效果。此外，對比峰峰值后發現，G-KSVD算法在對故障信號壓縮重構的過程中能夠增加脈沖信號的幅值，說明本文方法能夠增強故障信號中的沖擊成分，從而提高故障診斷的準確度。

4.3 基于ACFPER改進的G-KSVD0學習字典

為驗證引入ACFPER的學習字典的優越性，將時間優化前的學習字典稱為G-KSVD0學習字典，以此區分G-KSVD學習字典。采用燕山大學機械故障綜合模擬實驗臺的內圈故障數據，分別用傳統的K-SVD算法和G-KSVD0算法進行訓練，實驗結果如圖7所示。

圖7中，重構信號1為經過K-SVD算法重構所得的信號，重構信號2為經過G-KSVD0算法重構所得的信號。由圖7可知，三種信號幅值的上閾值均為0.5 m/s2，下閾值均為-0.5 m/s2。此外，由信號中峰值點的坐標可以看出，原始信號中沖擊信號的峰值最小，重構信號1次之，重構信號2中沖擊信號的峰值最接近閾值。由此可知，G-KSVD0算法在降低噪聲的同時，能夠增強信號中的沖擊成分，從而提高故障診斷的準確性。所得特征量數據見表7。

(a)原始信號

由表7可以看出，G-KSVD0算法的信噪比大于K-SVD算法的信噪比，說明G-KSVD0算法的去噪效果優于K-SVD算法，并且通過降噪處理提高了信號重構的精度，降低了噪聲部分對沖擊序列的影響。同時，G-KSVD0算法的峰峰值大

表7 G-KSVD0與K-SVD字典的實驗數據

于K-SVD算法的峰峰值，說明G-KSVD0算法所得信號的幅值大于K-SVD算法的幅值，信號得到了增強，方便故障特征的識別與提取。最后，為了判斷本文算法的魯棒性，對兩種算法求均方根值，由表7可知，G-KSVD0算法的均方根略小于K-SVD算法的均方根，說明經G-KSVD0算法重構后的信號分布更加穩定，受噪聲影響較小，有較好的魯棒性。但是G-KSVD0算法的運行時間大于K-SVD算法的運行時間，增加了算法的時間成本。

4.4 G-KSVD學習字典

G-KSVD0學習字典是從樣本中訓練而來，經過奇異分量的ACFPER計算，選擇包含脈沖序列較多的原子，對字典原子進行更新，進而得到有效的稀疏表示，實現信號的壓縮重構，減小了信號傳輸、處理上的壓力。然而，由于各原子的ACFPER指標計算增加了算法的運算復雜度，從而影響了算法的運行時間，增加了故障診斷的時間成本，故本文在字典更新階段采用減少反饋層的方法來減小算法的時間成本，構造新的學習字典G-KSVD。為了檢驗這一效果，分別利用改進的G-KSVD算法和K-SVD算法訓練數據，實驗結果如圖8所示，表8中的實驗數據是經過500次的重復實驗后求均值得到的。

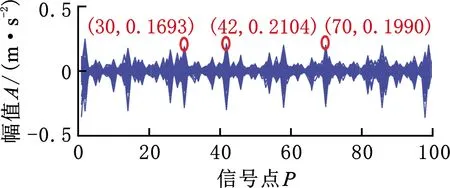
(a)原始信號

表8 G-KSVD算法、G-KSVD0算法與K-SVD算法的特征量均值

圖8中，重構信號1為經過K-SVD算法重構所得的信號，重構信號2為經過G-KSVD算法重構所得的信號。由圖8可以看出，算法經過減少反饋層之后，重構信號2中沖擊信號的幅值是最接近閾值的。由表8可知，雖然G-KSVD算法的降噪效果和魯棒性不及G-KSVD0算法，但是效果相差較小，而且G-KSVD算法的時間成本明顯小于G-KSVD0算法的時間成本。除此之外，G-KSVD算法的信噪比、峰峰值均大于K-SVD算法的信噪比、峰峰值，說明G-KSVD算法不僅能夠降低重構信號中的噪聲，而且可以增強信號中的沖擊成分。G-KSVD算法的均方根小于K-SVD算法的均方根，說明G-KSVD算法的魯棒性優于K-SVD算法的魯棒性。在時間方面，G-KSVD算法所耗時間均值為23.52 s，K-SVD算法所耗時間均值為34.59 s，由此可以看出，G-KSVD算法的運行時間明顯小于K-SVD算法的運行時間。因此，通過減少反饋能夠在保證精度的前提下有效地縮短算法的運行時間，從而達到降低時間成本的目的。

5 結論

(1)針對軸承信號復雜冗長的特性，本文在信號預處理過程中對信號進行分段，并對分段后的信號壓縮重構，從而提高信號分析的效率。同時，為了分析學習字典中原子間的相干性，本文提出自相關函數脈沖能量比這一指標，通過歸一自相關函數實現信號降噪的同時，通過Teager能量算子追蹤瞬時能量，增強重構信號中的沖擊成分，從而達到識別有效特征分量的目的。

(2)針對學習字典中缺乏的最優原子選擇問題，提出一種G-KSVD學習字典算法，該算法以ACFPER作為奇異值分解過程中有效奇異分量的選擇指標，通過有效的奇異分量實現最優原子的選取，形成新的學習字典。該算法不僅優化了降噪效果，而且增強了信號脈沖，提高了軸承信號重構過程中的準確度。

(3)由于ACFPER的求解會增加G-KSVD算法的計算復雜度，故本文在字典和系數矩陣的更新過程中通過減少反饋過程來降低時間對算法的影響。滾動軸承信號的實際實驗結果表明，本文算法所消耗的時間成本低于傳統K-SVD算法的時間成本。