基于固結試驗的Duncan-Chang參數反分析方法

王江營，雷 文，蔣中明,5，余元君，紀煒之，林 飛，張擁軍，王導勇

（1. 長沙理工大學水利工程學院，湖南 長沙 410114； 2. 湖南建工集團有限公司，湖南 長沙 410004；3. 湖南省洞庭湖水利事務中心，湖南 長沙 410007； 4. 湖南省水利水電勘測設計研究總院，湖南 長沙 410007； 5. 水沙科學與水災害防治 湖南省重點實驗室，湖南 長沙 410114）

土體變形計算是土力學三大主要問題[1]之一，國內外學者為此提出了種類繁多的本構模型和計算方法。大量的工程實踐表明，Duncan-Chang 模型具有很好的適用性和精確度[2～6]，特別是隨著各類數值計算軟件飛速發展，在土體變形計算中通常都需要用到Duncan-Chang 參數[5～7]。

眾所周知，Duncan-Chang 模型[2]共包含8 個參數，分別是C、φ、Rf、K、n、G、F 和D，需要通過三軸固結排水試驗進行測定，而對于許多中、小型工程來講，因為受制于經費預算和工期，往往不會開展這方面工作，進而會對后續計算分析造成影響。因此，一些專家在不斷研究在缺少試驗資料的情況下，如何近似推求土體的Duncan-Chang 參數。王志亮和殷宗澤等[3]基于土體K0狀態條件，針對缺少三軸試驗結果的情況，提出了可適用于砂土和黏性土的切線泊松比計算公式；曹文貴等[4]基于土體變形的非線性特征，充分考慮初始應力和附加應力對土體變形模量的影響，建立出了無需使用土體壓縮試驗曲線或靜載試驗曲線的Duncan-Chang 模型沉降計算方法；彭長學等[8]針對軟土壓縮曲線接近雙曲線方程的特點，提出以土體初始孔隙比和壓縮模量確定其e-p 曲線方程，進而可確定Duncan-Chang 模型的切線模量，但是這種方法無法考慮土體側向變形的影響；在此基礎上，楊光華等[9]利用e-p 曲線推求了軟土的非線性切線模量；孫明正等[10]結合具體工程，對已有的Duncan-Chang 模型參數推求方法進行了驗證和敏感性分析，計算結果顯示雖然存在一定偏差，但考慮到巖土工程的復雜性，仍具有較大的借鑒意義。

綜上所述可知，現有方法多是利用土體的e-p 曲線來推求其切線模量，并與Duncan-Chang 模型相結合，以用于沉降變形計算，但是其所能獲得的Duncan-Chang 參數比較有限，有關計算精度亦難以保證，且較為繁瑣。為此，本文擬通過對土體標準固結試驗進行數值模擬，并與其試驗所得的e-p 曲線相結合，以期建立出一種更加便捷可行的Duncan-Chang 參數反演分析方法。

1 Duncan-Chang 參數反演思路

Duncan-Chang 模型包含了8 個參數，其中粘聚力C 和內摩擦角φ 可通過直剪試驗求得，直剪中的慢剪與三軸固結排水試驗具有較好的共通性；土體的破壞比Rf一般在0.60～0.90 之間，當缺乏試驗數據時，可根據土體的種類近似取值，如黏性土的破壞比通常可取0.80，砂性土可取0.65[3]。

同時，在數值計算中K、n、G 和F 為常用參數，土體的切線彈性模量與切線泊松比與它們相關性較強，通常不會用到參數D[8-10]。因此，只需對K、n、G 和F 等參數進行反演，具體思路如下：

1）建立標準固結試驗數值計算模型，確定計算邊界條件、計算荷載及加載過程。

2） 擬定標準固結試驗數值模型初始Duncan-Chang 計算參數。

3）進行標準固結試驗的數值計算，獲得數值計算下土體e-p 曲線。

4） 重復變化標準固結數值試驗的Duncan-Chang 參數，再次進行數值計算，獲取新的數值計算ep 曲線。

5） 采用最小二乘法優化算法，建立Duncan-Chang 參數與e-p 曲線的非線性函數關系。

6）將標準固結物理實驗的e-p 曲線成果作為輸入條件，反求Duncan-Chang 參數。

7）將反求得到的Duncan-Chang 參數再次用于標準固結實驗的數值計算，獲得新的e-p 曲線。

8）對反演參數獲得的e-p 曲線進行誤差分析，當誤差滿足要求時，“6）”所求得的Duncan-Chang 參數即為最終結果。

2 標準固結試驗數值模擬計算

2.1 計算模型

根據土工試驗標準中標準固結試驗試樣制作標準，利用有限元軟件Ansys 建立一個直徑為6.18 cm，高為2.0 cm 的圓柱體壓縮試樣模型，并進行網格劃分，如圖1 所示，再將其導入有限差分軟件FLAC3D中，模擬標準固結試驗，試驗本構模型采用鄧肯-張非線性彈性模型+摩爾-庫倫模型。

圖1 標準固結試驗數值計算模型

2.2 標準固結試驗數值計算過程

首先，對圓柱體壓縮模型賦材料參數，其中C、φ值可由直剪試驗得到，約束圓柱試樣底面邊界和周圍邊界，對模型設定重力加速度，計算出試樣在自重作用下的位移并清除。

然后，根據標準固結試驗加載順序和步驟，按照壓力等級為50 kPa、100 kPa、300 kPa、400 kPa 對試樣進行逐級加載計算。

最后，利用Fish 語句編輯孔隙比、壓縮系數和壓縮模量計算式，輸出結果（e-p 曲線）。

由于FLAC3D只能通過Fish 程序獲取單元的體積應變增量和當前體積，無法直接獲取當前的孔隙比，因此，可通過一些推導來獲取單元體當前的孔隙比。

假定土體總體積為V，孔隙體積為Vv，固體顆粒體積為Vs，初始孔隙比為e0，荷載作用下體積變化量為ΔV，則土體體積應變εv為：

此時土體孔隙比e′為：

進而可得：

式中 e′——試樣體積變化后的孔隙比。

因此，在Fish 程序中，只需獲得每一級加載后試樣的體積應變增量，即可計算得到此時的孔隙比。針對4 組不同壓力，計算得到試樣固結穩定后的孔隙比，以孔隙比為縱坐標，壓力為橫坐標，即可得到相應的e-p曲線。

2.3 建立非線性函數關系

為了建立Duncan-Chang 參數與e-p 曲線的非線性函數關系，需擬定不同的初始參數，通過數值計算得到相應的e-p 曲線，然后采用非線性最小二乘法優化算法，建立它們之間的函數關系。

非線性最小二乘法是通過最小二乘分析，用m 個觀察點來擬合有n 個參數的非線性模型（m＞n），即考慮m 個數據點的集合，（x1，y1），（x2，y2），...，（xm，ym），以及一個曲線（模型函數）y=f（x，β），它除了變量x 外，還依賴于n 個參數β=（β1，β2，...，βn）。希望能找到參數矢量β，從而使得曲線在最小平方的意義上最好地擬合所給定的數據，也就是平方和最小，從而可建立出不同壓力p 下，土體孔隙比e 與Duncan-Chang 參數的關系式。

以湖南省沱江排水閘地基土為例，其初始孔隙比e0=0.67，通過擬定50 組初始參數，可以得到相應的ep 曲線，如表1 所示為不同參數和壓力下土體最終的孔隙比。

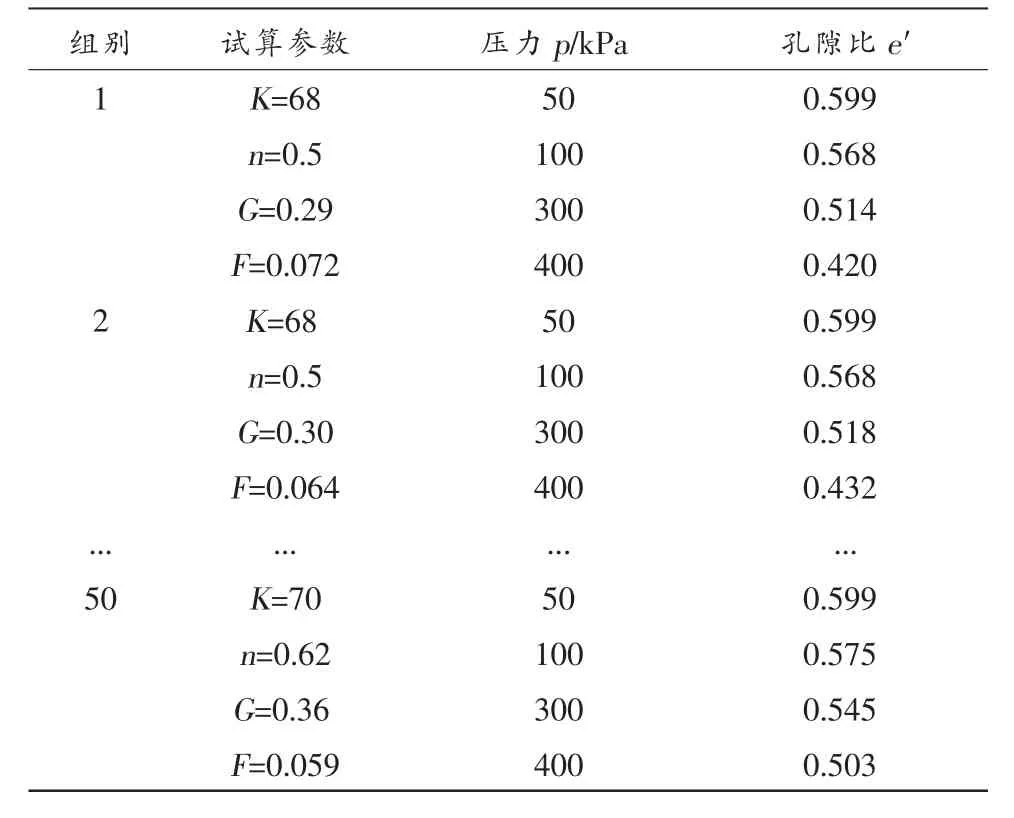
表1 土體孔隙比試算結果

進而，可擬合出壓力p 分別為50，100，300，400 kPa 時，土體孔隙比e 與K，n，G，F 等參數之間的函數關系式：

3 試驗驗證

將該土體標準固結物理實驗的e-p 曲線作為輸入參數，利用式（5）可求得到相關Duncan-Chang 參數：K=70.01，n=0.65，G=0.37，F=0.050。

進而，再將上述反求得到的Duncan-Chang 參數作為初始值，用于標準固結實驗數值模擬，又可得到不同壓力p 對應的孔隙比e，如表2 所示。

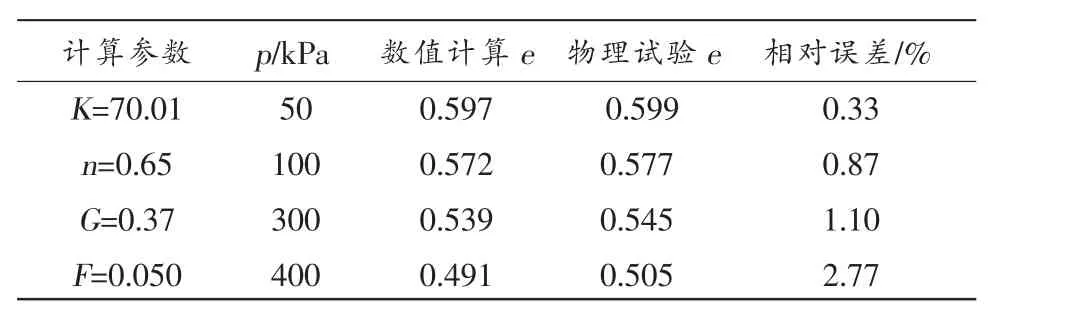
表2 不同方法下土體的孔隙比

同樣可求得此時的e-p 曲線，可將其與試驗結果繪制在一起，如圖2 所示。

圖2 不同方法下土體的e-p 曲線

由表2 可知，數值計算每級荷載作用下土體孔隙比e 與物理試驗實測值誤差較小，最大不超過3%；圖2 中數值模擬和物理試驗得到的e-p 曲線同樣偏差較小，其精度可滿足要求。此時，可認為由式（5）反求得到的Duncan-Chang 參數即為最終結果，表3 所示為反演計算結果和三軸固結排水試驗的實測結果。

表3 土體Duncan-Chang 參數反演值與實測值

由表3 可知，本文方法所得結果相對文獻[3]方法的結果更為理想。其中，K、n、G 等3 個參數的相對誤差較小，最大不超過5%，而F 值相對誤差較大，這是由于F基數很小，對數值模擬結果比較敏感，但誤差范圍仍在10%以內，對于數值計算來講是相對可以接受的，即表明了本文所提出的Duncan-Chang 參數反演分析法是合理可行的。

4 結 論

1）利用有限差分軟件FLAC3D，利用Fish 語句編輯土體孔隙比、壓縮系數和壓縮模量的計算公式，建立了土體標準固結試驗數值計算方法。

2）基于土體標準固結試驗數值計算結果和最小二乘法優化算法，建立出了Duncan-Chang 參數反分析方法。

3）本文建立的Duncan-Chang 參數反分析方法合理可行，能夠滿足相關數值計算要求。