北方某水庫邊坡蓄水響應特征研究

王詠梅

(天津市武清區水務局，天津 301700)

1 引言

我國作為一個水利大國，在水利水電工程的修建、運營過程中難以避免地會遇到一些不穩定庫岸邊坡，面對這類棘手的工程地質難題，水利行業內越來越多的學者、技術人員逐漸意識到，對不穩定斜坡的變形機制進行研究具有十分重要的意義[1-5]。目前國內外學者對已經做了很多研究[6-8]。

通過文獻調研發現，近年來，行業相關人員圍繞這類課題做的工作主要集中于以下幾個方面：以實際工程為研究背景，將施工過程和地質體的關系耦合起來協同研究[9]。抑或者是將傳統的傳遞系數法與地理信息技術(如ARCGIS)相結合，不僅可解決穩定性定量計算，還可實現穩定性分區[10-11]，除了與現場結合越來越緊密，并進行跨學科研究之外，還有學者將傳統的穩定性計算方法進行了改良，提出了與現場實際情況更為接近的穩定性評價方法[12]，這些科研成果都在一定程度上推動著行業的不斷革新、進步。

本文以北方某水庫邊坡作為研究對象，重點對蓄水過程邊坡的應力應變特征和對應的穩定性系數情況進行分析，揭示邊坡的變形機理，并提出處理措施，并予以驗證。

2 工程案例概況

研究區水庫是黃河流域中的梯級水庫，總庫容3947萬m3，正常蓄水位229.00 m。

工程區地形相對高差100 m～150 m，庫區右岸以侵蝕堆積的低中山為主。庫區左岸上游有面積不大的夷平面零星殘留于山地頂部，地貌形態以侵蝕溶蝕的低中山為主。庫區左岸下游，僅可見一相對較為寬闊的剝蝕面以及馬蹄河與明月河之間的地形分水嶺。庫區主要出露巖性主要為千枚巖、板巖、變質砂巖。

自2018年3月一期蓄水開始后某庫水邊坡出現輕微變形，至2018年5月二期蓄水后變形量開始逐漸增加，對水庫的運營構成了極大的威脅，本文主要依據此案例，對其變形成因進行數值計算分析。

3 多場耦合的數值計算前處理

3.1 計算模型設計

結合現場實際情況，使用二維有限元計算程序建立數值計算模型，見圖1。

圖1 原始計算模型

如圖1所示：千枚巖、變質砂巖、板巖的網格單元尺寸范圍為1 m～5 m，為提高計算精度，對坡表千枚巖網格進行加粗，網格形狀以四邊形為主，局部采用三角形單元控制。邊坡底面邊界長度為398 m，左側邊界高度為198 m，右側邊界高度為62 m。側面邊界采用X向位移、速度固定約束，底面采用Y向位移、速度固定約束。地下水位線結合現場鉆探情況進行標定，圖1中采用虛箭頭線表示。

合理的參數選取是進行正確的穩定性分析與治理工程設計的前提。通過室內試驗取值、參數反算、與工程經驗類比相結合，綜合選取工程區滑坡的巖土體物理力學參數，選取成果見表1。

表1 巖土體物理力學參數綜合取值

3.2 工況與模擬方案標定

本次數值計算主要考慮以下三種工況：

(1)工況一：一期蓄水(僅考慮自重，g=9.8 m/s2，對應的蓄水位高程為234 m)

(2)工況二：二期蓄水(僅考慮自重，g=9.8 m/s2，對應的蓄水位高程為256 m)。

(3)工況三：二期蓄水+治理措施(在工況二的基礎上，結合工況二的計算結果選定治理措施。)

數值計算方案：

(1)工況一將有限元軟件中的SWEEP/W和SIGMA/W模塊相結合，按實際情況繪制水位線，兩側邊界設置水頭，材料滲透系數利用Van Genuchten估計方法，結合體積含水量反推滲透系數，在滲流場計算結果的基礎上，引入應力、應變分析模塊，對邊坡的響應特征進行分析。

(2)工況二：完成初步分析后，按照二期蓄水位添加水頭，進行應力重分布分析，并引入SLOPE/W模塊，材料參數不變，滑移面的判定結合工況一的最大剪切面進行標定，計算出穩定性系數。

(3)工況三：在前面兩種工況分析的基礎上，分析治理方案對蓄水邊坡的影響，具體計算方案主要依據工況二的計算結果進行。針對削方、回填反壓這種措施，主要通過賦予null或新的材料單元(區域)進行；針對抗滑樁、擋土墻、框架格構這種承受三向荷載的措施，采用結構梁模擬；針對預應力錨索、預應力錨桿這種主要考慮軸力、剪切力的工程措施，采用結構桿件進行模擬，完成治理方案的應力應變分析后再進行SLOPE/W應力平衡計算，驗證這種方案的可行性。

4 數值計算成果及分析

4.1 工況一計算結果及分析

圖2～圖5為工況一的研究區邊坡的數值計算結果。

圖2 工況一最大總應力

圖3 工況一最小總應力

圖4 工況一最大剪應變

圖5 工況一合位移

由圖可知：在一期蓄水作用下，最大總應力仍然與天然重力場基本一致，應力量值與重力方向相同，量值大小與埋深呈正比，受壓應力控制。最小主應力與最大主應力呈近似正交的關系。由此可見：場地所在的應力環境條件對整體、局部穩定性有利，最大剪切應變方面，在板巖底面邊界出現了應變集中，但量值較小，從位移量值上可以體現出來，最大位移量約3 mm，位移較小，可忽略不計，整體處于穩定狀態。

4.2 工況二計算結果及分析

圖6～圖10為研究區邊坡在二期蓄水作用下的計算結果云圖。

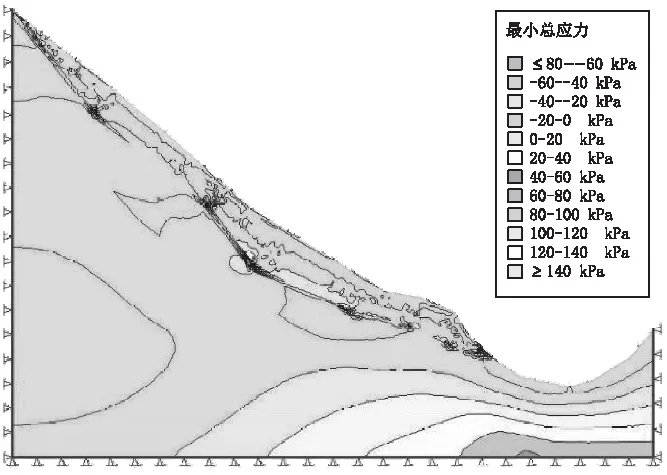
圖6 工況二最小總應力

圖7 工況二最大剪應變

圖8 工況二合位移

圖9 工況二網格變形趨勢

圖10 工況二穩定性計算結果

由最小總應力圖可看出，最小總應力呈條狀分布，隨著深度的增加而增加，壓應力主要以重力場為主，最小總應力負值(拉應力區)主要出現在板巖坡表以及板巖、變質砂巖交界處，應力集中以陡緩交界處最為明顯)，拉應力最大值約80 kPa。

最大剪應變方面，與工況一相比，有增加的趨勢，最大達到0.064，最大位移達到8 cm，從變形趨勢圖上可以發現變形主要分為兩段，邊坡中上部出現沉降，中部出現輕微擠壓但位移量較小，邊坡中下部出現沉降，下部出現擠壓，于巖體分界面處剪出，板巖與變質砂巖的分界面為軟弱面，以此為依據，進行穩定性計算，系數值為0.975，處于不穩定狀態。

根據以上分析，認為水庫二期蓄水后，導致邊坡出現變形，整體處于不穩定狀態，需要采取治理工程措施。

4.3 工況三計算結果及分析

在前面的分析中發現：邊坡中上部與邊坡中下部對整體穩定性至關重要，結合行業工程經驗，認為采用回填反壓存在幾何空間不理想的問題，且盲目大挖大刷可能造成變形體擾動，導致邊坡出現整體失穩，而采用抗滑樁、擋土墻進行治理更是無從下手，因此在“削”“壓”和“支”“擋”都難以實現的基礎上，建議使用錨固措施，推薦采用“框架格構梁+預應力錨索”相結合的方式進行處置，治理方案見圖11，預應力錨索細部見圖12、圖13。

圖11 工況三計算模型

圖12 預應力錨索結構設計圖

圖13 錨頭大樣圖

框架梁使用C30鋼筋混凝土現場立模現澆施工。錨墩為0.6 m×0.6 m×0.4 m，框架截面為0.3 m×0.3 m，每片框架由6～7根豎肋和相應的橫梁組成，施工時盡可能一次澆筑完成，當分兩次澆筑時，豎肋間設置后澆帶。兩片框架間宜設置伸縮縫，寬2 cm，內填瀝青麻筋。

錨索材料采用高強度低松弛4根φs15.2 mm的預應力鋼絞線組成，錨具用OVM15-4型，錨索長度15 m，自由端長度5 m，預應力施加1000 kN。

建立數值模型后，進行計算分析，計算結果見圖14～圖16。

圖14 工況三最大剪應變

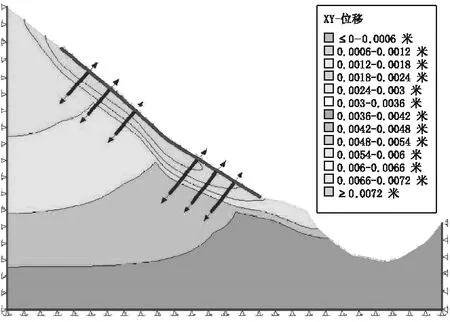
圖15 工況三合位移

圖16 工況三穩定性系數計算結果

計算結果顯示：工況三的最大位移變形量降低為7 mm左右，最大剪應變量值相比工況二降低了96.56%，對應的穩定性系數值提升至1.325。由此可見：采用“框架格構梁+預應力錨索”治理是相對比較可靠的。

5 結論

本文以北方某黃河庫區庫岸邊坡為研究對象，調研了場地的工程地質條件，結合現場情況建立了工程地質模型，根據蓄水情況設計了數值計算方案，進行了滲流、應力應變場耦合計算，并進行了基于應力平衡法的穩定性計算，結合計算結果提出了治理措施，并沿用先前建立的技術手段進行對比驗證，在這個過程中，得出了以下四點主要結論，以期為類似工程提供參考依據：

(1)針對由千枚巖、變質砂巖、板巖等變質軟巖組成的庫水邊坡，在研究蓄水響應特征這類問題時，采用有限元軟件進行滲流、應力場耦合數值計算是基本可行的，今后對類似問題的研究可考慮采用這種技術手段作為參考。

(2)研究區邊坡在一期蓄水位下的最大總應力場與天然重力場基本一致，應力量值與重力方向相同，量值大小與埋深呈正比，受壓應力控制。最小主應力與最大主應力呈近似正交的關系，整體受壓應力控制，最大位移量約3 mm，可忽略不計，整體處于穩定狀態。

(3)研究區邊坡在二期蓄水位下，最小總應力呈條狀分布，隨著深度的增加而增加，壓應力主要以重力場為主，最小總應力負值(拉應力區)主要出現在板巖坡表以及板巖、變質砂巖交界處(以陡緩交界處最為明顯，甚至出現了應力集中)，板巖與變質砂巖的分界面為軟弱面，穩定性系數為0.975，處于不穩定狀態。

(4)研究區邊坡中上部與邊坡中下部的穩定性對整體穩定性至關重要，結合行業工程經驗，建議采用“框架格構梁+預應力錨索”結合的方式進行治理，計算結果顯示：最大位移變形量降低為7 mm左右，最大剪應變量值相比工況二降低了96.56%，對應的穩定性系數值增加至1.325。由此可見：采用這種方案進行治理是相對可靠的。