盾構機球軸承內環鑄造生產工藝研究
張洪浩,胡愛國,劉吉利
(濟南二機床集團鑄造有限公司,山東濟南 250400)
1 盾構機球軸承內環鑄件結構及質量要求
球軸承內環為盾構機伸縮擺動式主驅動組件關鍵零部件。零件設計尺寸SR4000mm,高1250mm,平均壁厚220mm,毛坯尺寸?8060mm,高1385mm,毛坯重57.4t,屬超大尺寸厚大斷面球鐵件。零件材質為QT400-18L,屬于高韌性鐵素體球墨鑄鐵,主要應用于風電、高鐵等關鍵零部件生產。材質要求-20℃低溫沖擊功平均值Kv≥12J;鑄件本體球化不低于3 級;超聲波探傷符合EN12680-3-2003 二級探傷要求。
1.1 盾構機球軸承內環造型工藝
因鑄件尺寸超出鑄造公司現有造型裝備能力,現有工裝無法滿足生產要求且工裝配置困難。采用地上圍坑方案,利用現有工裝組合,實現超尺寸鑄件生產需求,解決無工裝問題。采用三維軟件模擬實際圍坑操作,解決圍坑方案實施性問題,如圖2~8 所示。

圖1 盾構機球軸承內環結構
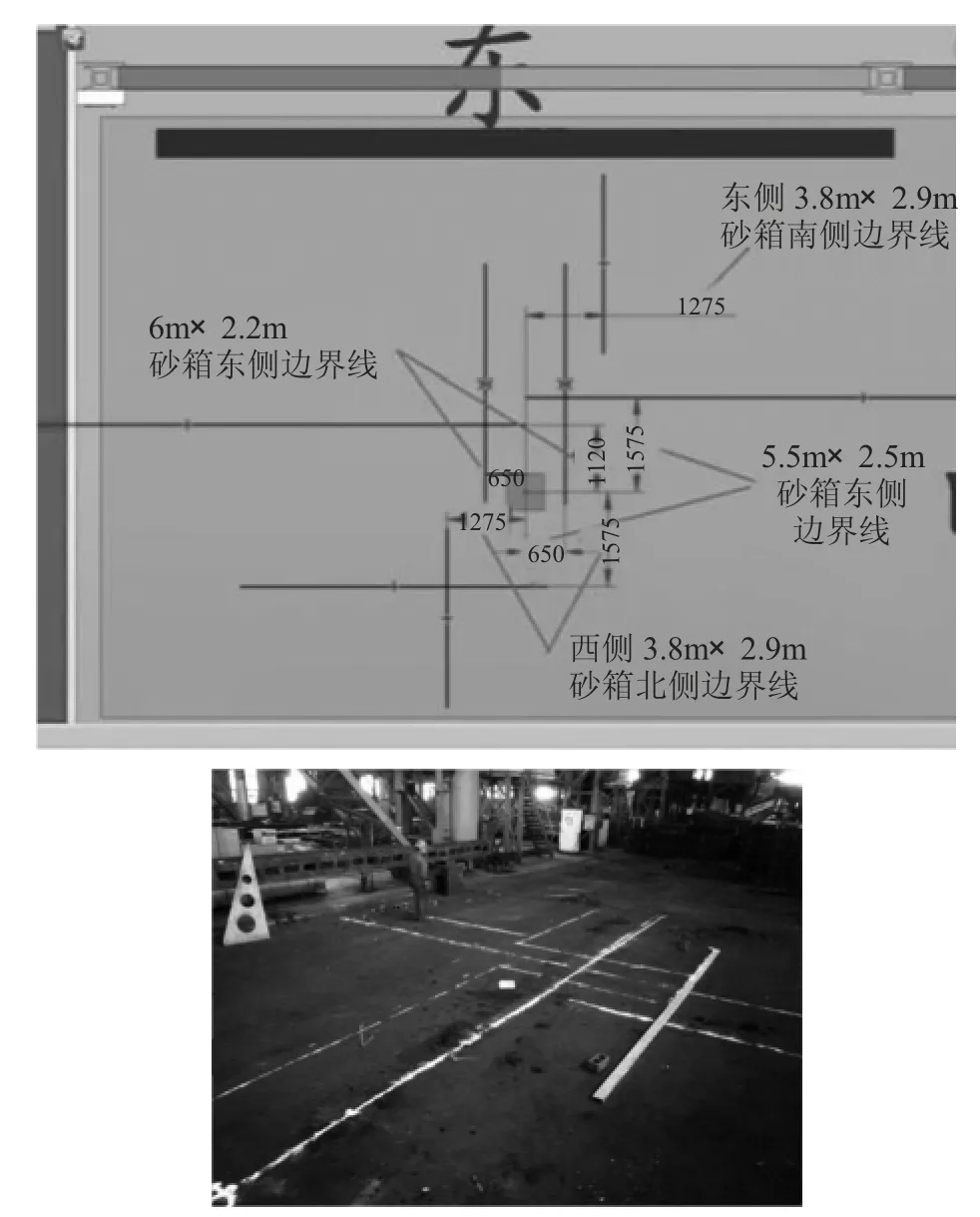
圖2 模擬及實際操作流程-底箱基準
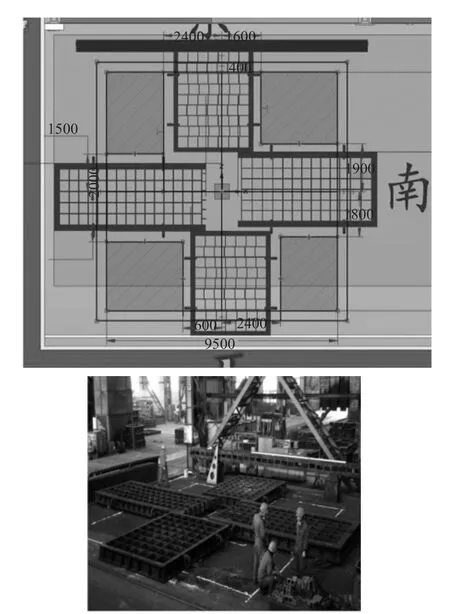
圖3 模擬及實際操作流程-底箱及邊界

圖4 模擬及實際操作流程-鋪底砂胎及圍坑平臺

圖5 模擬及實際操作流程-配模初期及檢測

圖6 模擬及實際操作流程-配模后期及檢測

圖7 模擬及實際操作流程-填砂

圖8 模擬及實際操作流程-蓋箱放置、方杠背緊
1.2 造型過程質量控制
實際生產過程中尺寸保證難度大。采取地上圍坑操作,生產占用面積較大且無專用造型平臺,液態金屬漲箱力巨大,極易因控制尺寸及圍坑結構保證性不強,造成鑄件尺寸精度不足而導致報廢,如圖9 所示。須綜合運用各種控制手段,解決4200kN(420t)脹箱力問題。(1)生產現場采用鋼質砂箱制作水平基準面骨架,解決樹脂砂基準面整體強度問題,如圖10 所示。(2)創新設計箍芯裝置,如圖11 所示,將各個泥芯的芯骨延長后焊接到一起,拓展芯鐵用途,提高鑄型結構強度。有限空間內實現鑄型無工裝自持,解決漲型問題;實現無蓋箱、無壓重,解決壓重操作問題。(3)制作平臺連接工裝,如圖12 所示,便于圍坑平臺操作,解決平臺連接處牢固問題。(4)采用砂箱+緊箱方杠組合,如圖13 所示,多點抄手背緊,實現平臺主體結構保證性。(5)澆注前逐一檢查196 處背點,如圖14 所示,保證各背點有效受力,確保上述措施有效。
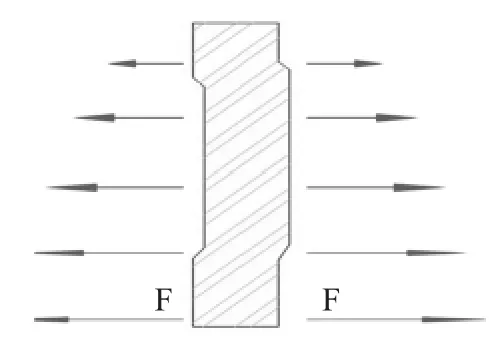
圖9 脹箱力示意圖

圖10 保證造型基準面強度
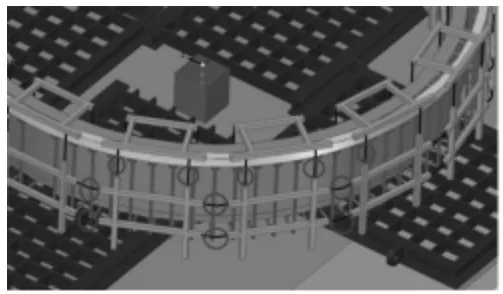
圖11 箍芯裝置示意圖
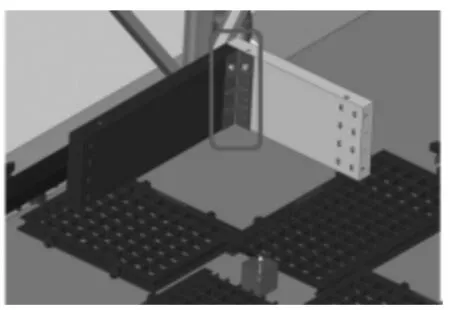
圖12 角接工裝
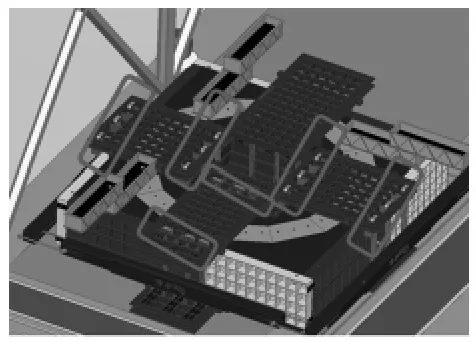
圖13 砂箱+緊箱方杠組合

圖14 檢查各背點
2 盾構機球軸承內環熔煉及澆鑄工藝
該鑄件工藝毛重57.4t,出鐵67t,后跟熱鐵水沖點澆口。成份控制如表1 所示,球化處理工藝參數如表2 所示。

表1 化學成分 w/%

表2 球化處理工藝參數
2.1 熔煉
(1)爐內只加生鐵、廢鋼,生鐵廢鋼加入配比:生鐵90%,廢鋼10%,爐內硅鐵、錳鐵等化驗完后再加。
(2)熔化到1450℃,扒渣取樣,化驗調整成分,繼續升溫到1520℃等待出鐵。
(3)專用孕育劑要烘烤后使用。
2.2 澆注
熔煉過程中要注意以下幾點:扒渣要干凈;注意點火、引氣、擋渣;澆注溫度1335~1345℃。
3 結束語
盾構機球軸承內環鑄件的順利產出,打破鑄造公司回轉體鑄件歷史記錄,實現國內首臺套重大設備關鍵零部件國產化,打開大型基建設備零部件市場,為今后拓展市場打下良好口碑。

