基于集成學習的改進灰色瓦斯濃度序列預測*

賴祥威，夏云霓，鄭萬波，崔俊飛，吳燕清，史耀軒

(1.昆明理工大學 理學院,云南 昆明 650500；2.昆明理工大學 數據科學研究中心,云南 昆明 650500；3.重慶大學 計算機學院，重慶 400030; 4.中煤科工集團重慶研究院有限公司，重慶 400037；5.瓦斯災害監控與應急技術國家重點實驗室，重慶 400037；6.重慶大學 資源及安全學院，重慶 400030)

0 引言

瓦斯濃度預測是煤礦安全生產重要環節。國內學者針對瓦斯預測開展研究:楊麗等[1]基于多元分布滯后模型(MDL)提出多變量瓦斯濃度時間序列預測模型;胡坤等[2]為準確預測瓦斯涌出量，建立回采工作面瓦斯涌出量優化預測模型;李冬等[3]為提高瓦斯突出危險區域預測精度，建立瓦斯突出危險區域綜合預測方法;李成武等[4]為預測礦區突出能量，通過引入煤體當量半徑，推導突出能量預測模型；張友誼等[5]通過研究灰色關聯模型輸出端與輸入端，提出煤與瓦斯突出多指標耦合預測模型。此外，國內部分學者基于神經網絡、隨機森林等時間序列進行預測研究[6-8]，但均需基于大量數據，針對信息匱乏的時間序列研究，灰色理論在能源消費、電網安全運作能力等眾多領域得到充分運用[9-15]，但在煤礦瓦斯預測領域研究較少。現有煤礦瓦斯濃度預測方法為傳統灰色預測模型，但傳統灰色預測模型灰色作用量為常量，不隨時間發生變化。因此，本文通過對傳統灰色模型進行優化，得到隨時間改變的冪指數灰色作用量，并提出基于集成學習的冪指數型灰色瓦斯濃度預測模型，研究結果可有效提瓦斯濃度預測精度。

1 預測算法設計流程與評價分析

灰色預測在解決不確定性問題，尤其對于小樣本時間序列問題具有一定優勢。通過將歷史數據序列累加得到生成序列，建立灰色預測模型，實現對未來發展趨勢預測。

1.1 傳統灰色預測模型

傳統灰色預測模型建立主要包括以下5個步驟：

1)設原始瓦斯濃度序列如式(1)所示：

(1)

經1次累加生成瓦斯濃度序列，如式(2)所示：

(2)

經1次累減生成瓦斯濃度序列，如式(3)所示：

(3)

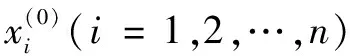
2)X(1)緊鄰均值生成序列如式(4)所示：

(4)

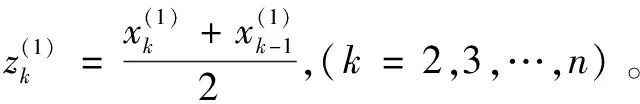
3)傳統灰色預測模型如式(5)所示：

(5)

式中：k=2,3,…,n。

利用1階單微分方程擬合,得到傳統灰色預測模型白化方程，如式(6)所示：

(6)

式中：a為發展系數;b為灰色作用量。

4)在傳統灰色預測模型中，利用最小二乘法進行參數估計，向量u，Y,B分別如式(7)～(9)所示：

u=[a,b]T=(BTB)-1BTY

(7)

(8)

(9)

基于式(7)～(9)求解傳統灰色模型白化方程,得到瓦斯濃度響應序列，如式(10)所示：

(10)

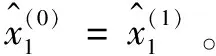
5)利用1次累減生成瓦斯濃度序列，得到瓦斯濃度預測值序列，如式(11)所示：

(11)

1.2 優化后冪指數型灰色預測模型

實際問題中，灰色作用量隨時間變化而變化。因此，本文通過對灰色作用量進行優化，得到冪指數型灰色作用量，建立改進后灰色預測模型。主要包括以下5個步驟:

1)將傳統灰色預測模型對應白化模型靜態灰色作用量替換為冪指數型灰色作用量，即將b替換為beαk+c(其中α為參數)，得到改進后灰色預測模型白化模型，如式(12)所示：

(12)

改進后灰色預測模型如式(13)所示：

(13)

式中：c為參數。

2)設向量Y,B如式(14)～(15)所示：

(14)

(15)

式中：β=a-1(eα-1)。

參數估計向量u如式(16)所示：

向量u=[a,b,c]T=(BTB)-1BTY

(16)

3)假設任意函數μ(k)滿足式(17)：

μ′(k)=aμ(k)

(17)

通過求解可得式(18)：

μ(k)=heak

(18)

式中：h為常數。

4)將式(12)兩邊同乘μ(k)并積分，如式(19)～(21)所示：

(19)

(20)

(21)

式中：C為常數。

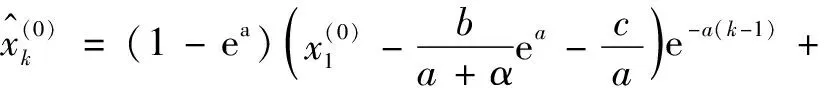
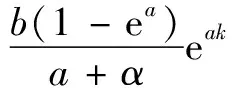
(22)

式中：k=1,2,…,n；a,b為常數。

1.3 基于集成學習的冪指數型灰色預測模型

集成學習通過將多種不同模型按照權重加權組合得到新預測模型。本文采用標準差法得到瓦斯濃度組合預測模型權重，進行瓦斯濃度預測。組合預測模型構造流程如圖1所示。

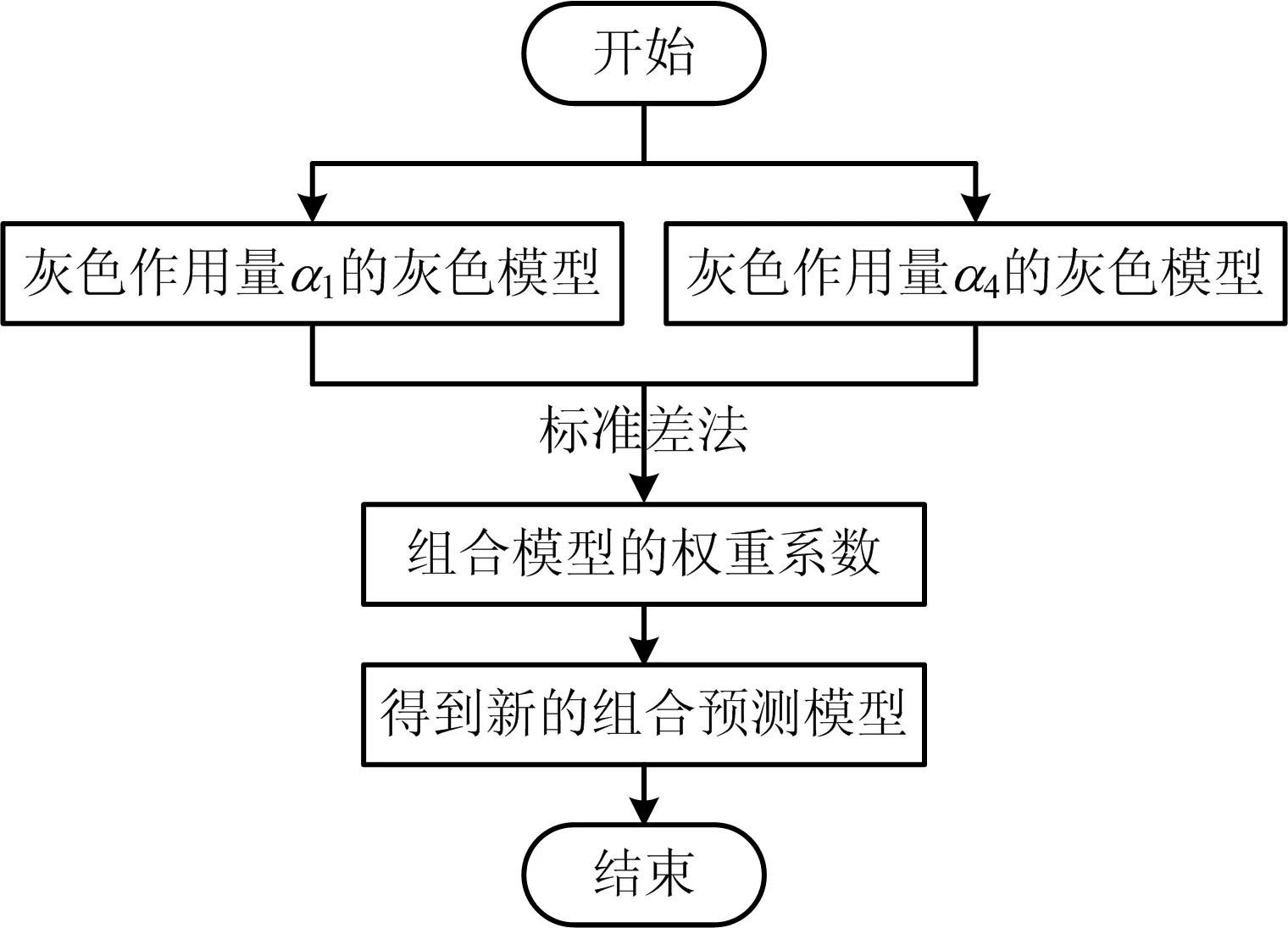
圖1 組合預測模型構造流程

(23)

同時，需滿足預測誤差平方達到最小準則，如式(24)～(25)所示：

(24)

(25)

式中：xk為k時刻瓦斯濃度實際值，%。

1.4 模型評價指標

本文采用均方根差(RMSE)與平均絕對誤差(MAE)對不同算法預測精度進行科學評價。均方根差與平均絕對誤差如式(26)～(27)所示：

(26)

(27)

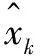
2 瓦斯濃度預測仿真實驗

2.1 實驗數據

本文以吉林八連城礦井為研究背景，基于八連城瓦斯監控數據，采用不同算法進行預測，并對實驗結果進行討論分析。實驗數據來源于八連城煤礦瓦斯災害風險管控平臺2021年1月1日至2021年2月1日以及2021年2月1日至2021年2月4日長期與短期瓦斯監控數據。八連城煤礦瓦斯災害風險管控平臺如圖2所示。

圖2 八連城煤礦瓦斯災害風險管控平臺

瓦斯濃度監控傳感器數據24 h不間斷采集(極少部分數據缺失)，瓦斯濃度序列數據時間間隔1 h。選取其中2個礦井工作面(南11902上順工作面、北12005上順工作面)監測數據作為實驗數據。以數據集前75%數據作為訓練集，剩余25%數據作為測試集。2個礦井工作面瓦斯濃度傳感器采集數據周期見表1。

表1 2個礦井工作面瓦斯濃度傳感器采集數據周期

2.2 實驗結果

采用瓦斯濃度序列傳統灰色預測模型，冪指數型灰色預測模型及基于集成學習的指數型灰色預測模型，對礦區南11902上順工作面、北12005上順工作面數據集瓦斯濃度數據進行預測，并對預測誤差進行分析。

1)南11902上順工作面不同預測模型預測值與誤差分析

不同模型訓練集與測試集絕對誤差如圖3所示，不同模型下預測值誤差分析見表2。由表2可知，相較于瓦斯濃度傳統灰色模型，冪指數型模型與集成學習模型平均絕對誤差及均方根差均有所降低；在訓練集短期預測中，基于集成學習的指數型預測模型誤差相對較小，較傳統灰色預測模型平均絕對誤差和均方根差分別下降1.27%，1.26%；長期預測中，基于集成學習的指數型預測模型較傳統灰色預測模型平均絕對誤差和均方根差分別下降1.76%，2.25%。

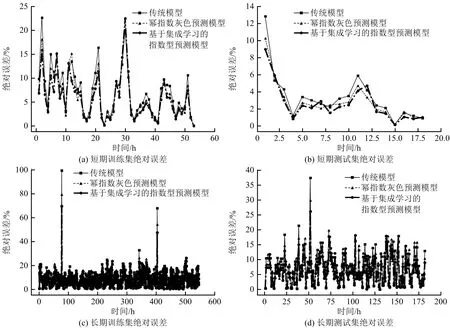
圖3 南11902上順工作面不同模型絕對誤差

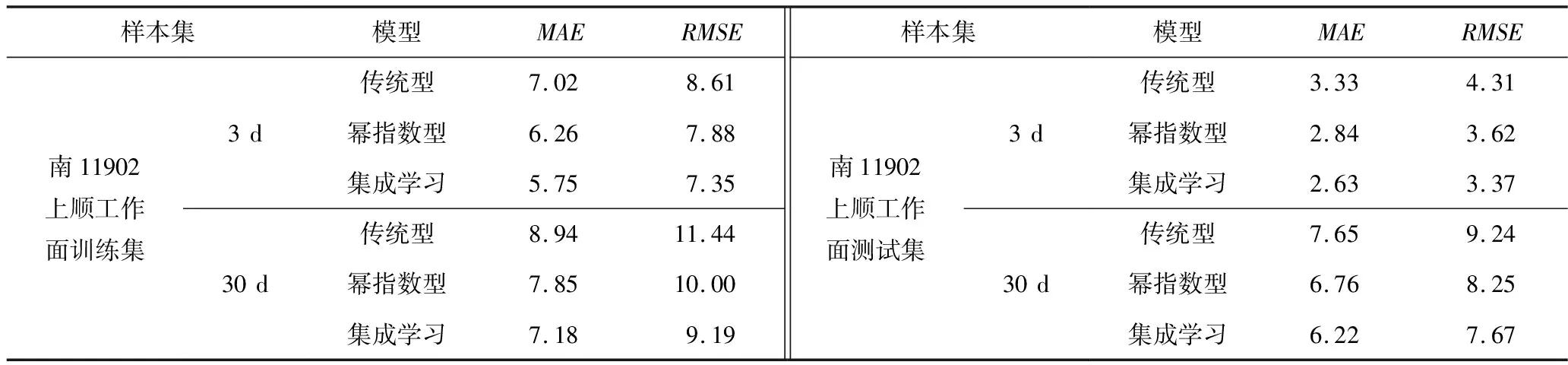
表2 南11902上順工作面不同模型下預測值誤差

在測試集短期預測中，基于集成學習的指數型預測模型誤差相對最小，較傳統灰色預測模型平均絕對誤差和均方根差分別下降0.7%，0.94%；長期預測中，平均絕對誤差和均方根差分別下降1.43%，1.57%。

2)北12005上順工作面不同模型預測值及誤差分析

不同模型訓練集絕對誤差與測試集絕對誤差如圖4所示，以不同模型下預測誤差分析見表3。由表3可知，相較于瓦斯濃度傳統灰色模型，冪指數型模型與集成學習模型平均絕對誤差和均方根差均有所降低。在訓練集短期預測中，集成學習模型誤差相對最小，較傳統型平均絕對誤差和均方根差分別下降0.51%，0.45%；長期預測中，集成學習模型較傳統型平均絕對誤差和均方根差分別下降0.95%，1.99%。

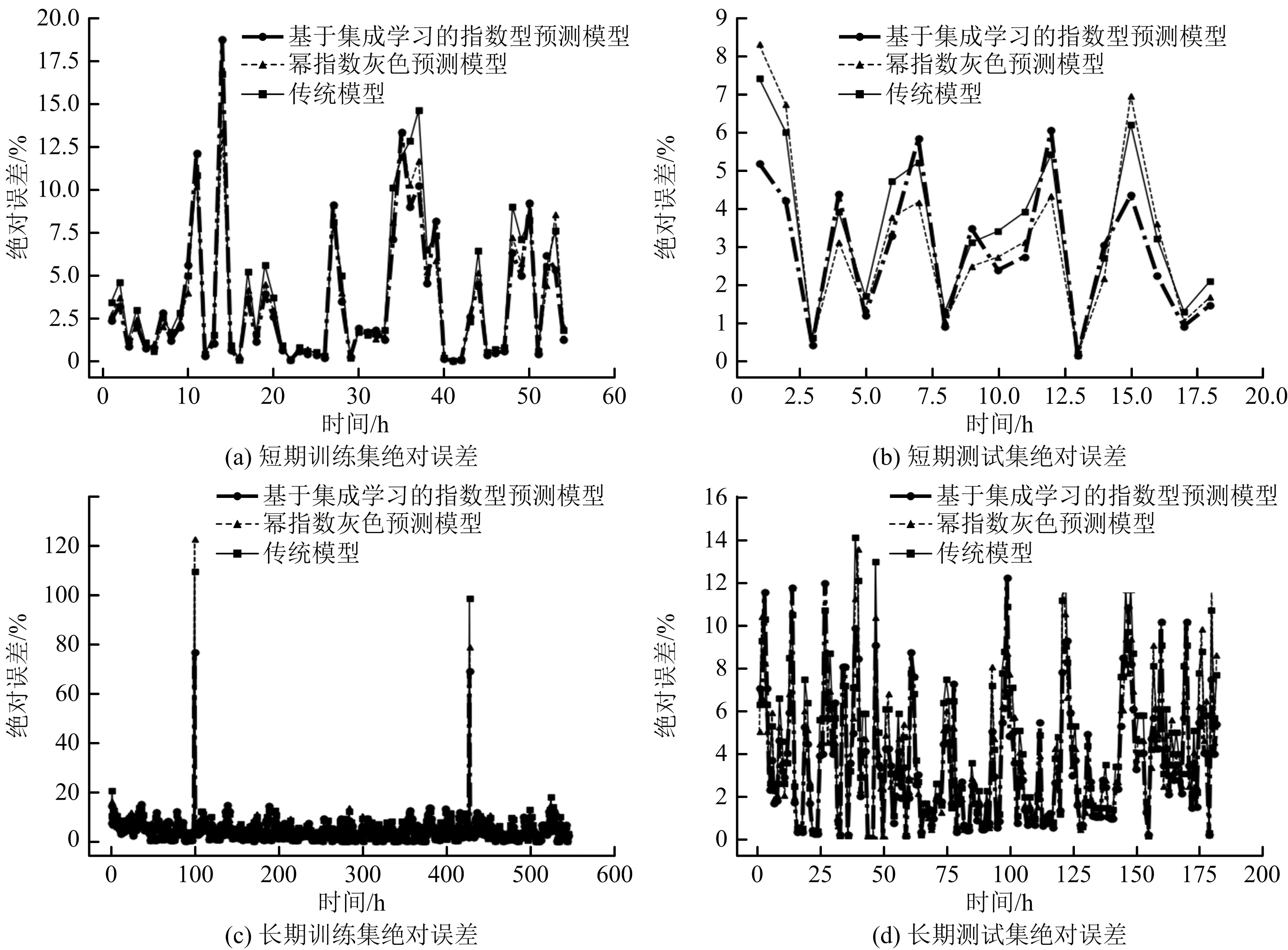
圖4 北12005上順工作面不同模型的絕對誤差

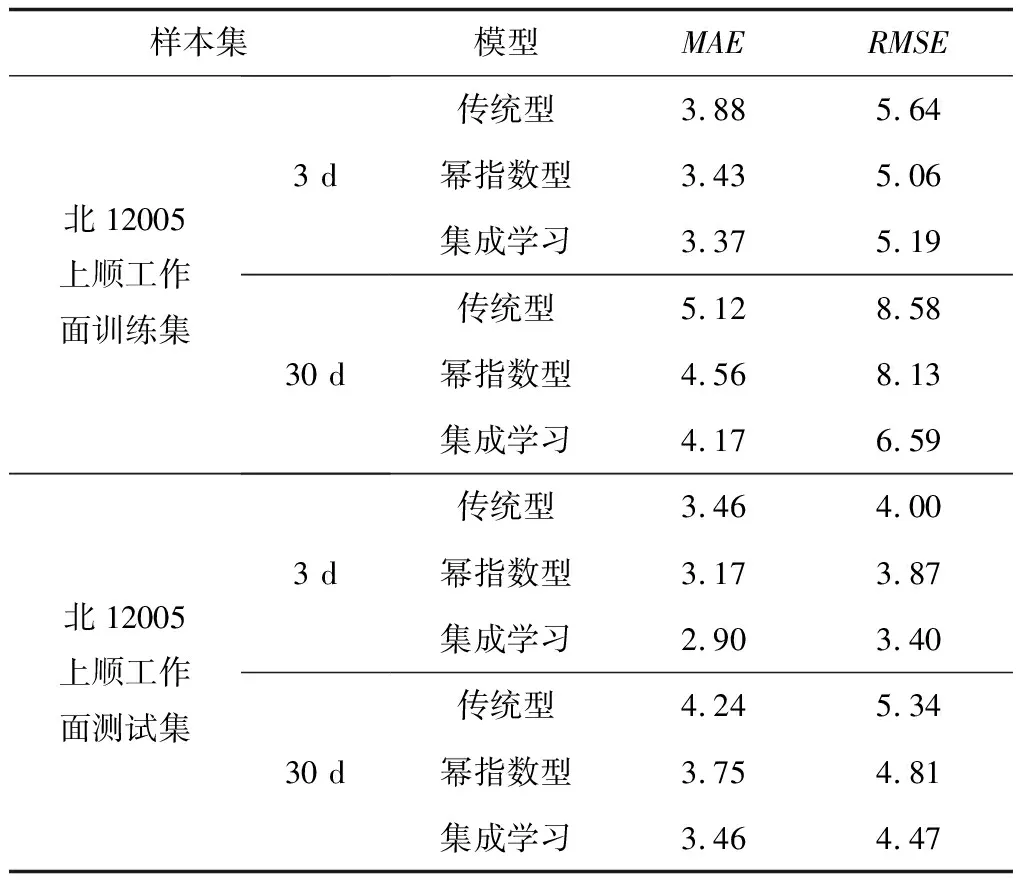
表3 北12005上順工作面不同模型下預測誤差分析

在測試集短期預測中，集成學習模型誤差相對最小，較傳統型平均絕對誤差和均方根差分別下降0.56%，0.6%；長期(30 d)預測中，平均絕對誤差和均方根差分別下降0.78%，0.87%。

綜上，本文提出的基于集成學習的改進灰色瓦斯預測模型相較于傳統灰色模型預測值誤差更小，預測精度更高。

3 結論

1)基于集成學習的改進灰色瓦斯預測算法有效降低瓦斯濃度預測值與實際值絕對誤差及均方根誤差，瓦斯濃度序列均方根差最大降低2.25%，尤其針對瓦斯濃度時間序列為近似線性情況時，預測效果較好。在算法設計方面，考慮瓦斯濃度序列混沌特性，對混沌特性數據具有普適性。

2)基于集成學習改進灰色瓦斯濃度預測算法預測精度方面仍有較大上升空間。研究結果為智慧煤礦瓦斯預警提供借鑒。