基于UHBs的輸氣管道高后果區泄漏燃爆事故分析

遲明華，蔣宏業，趙新好，徐濤龍

(1.西南石油大學 石油與天然氣工程學院，四川 成都 610500；2.油氣管道技術研究院，四川 成都 610500；3.國家管網集團公司西氣東輸分公司，上海 200122)

0 引言

隨著我國的天然氣消耗的增加，越來越多輸氣管道穿越人口密集區等特殊場所，形成高后果區[1]；其內輸氣管道一旦發生泄漏燃爆事故將會造成極大破壞[2]。而在輸氣管道事故風險可能性影響因素中，人的不安全行為導致的第三方破壞具有突發性高、隨機性大以及難以防控等特點，一直被列為4大類風險因素之首[3]。因此，基于人的不安全行為對輸氣管道高后果區進行泄漏燃爆事故分析具有重要意義。

Bow-tie模型是全面分析某一事件發生原因和事故后果的方法[4]，在油氣管道失效和后果分析上有著一定的應用[5-6]，但Bow-tie模型存在著2個弊端：1)事件狀態具有二態性，故障邏輯關系具有確定性；2)只能按照結構從底至頂逐層推理計算頂事件的發生概率，計算量大且不能逆向推理。這2點弊端限制了Bow-tie模型在工程實際上的應用，宋華等[7]所提出的T-S模糊故障樹分析方法，考慮了故障概率和事件間聯系的不確定性，改進了傳統Bow-tie模型的弊端；胡顯偉等[4]、於孝春等[8]便采用改進后的模糊Bow-tie模型(Fuzzy Bow-tiemodel，FBT)對燃氣管道和深水海底管道進行定量風險評價。而貝葉斯網絡(Bayesian Networks，BN)在雙向計算和描述事件多態性、非確定性邏輯關系上有顯著優勢[9]，可以彌補Bow-tie模型的弊端。

本文結合T-S模糊故障樹、Bow-tie模型和貝葉斯網絡3種方法，從人的不安全行為發生的可能性出發，建立不同等級人口敏感區輸氣管道泄漏燃爆事故FBT-BN分析模型對輸氣管道高后果區泄漏燃爆事故易發性和事故致因進行分析。

1 基本理論和方法

1.1 基于T-S模糊故障樹的模糊Bow-tie模型

引入T-S模糊故障樹[7]，建立基于T-S模糊故障樹的模糊Bow-tie模型，簡單模型如圖1所示。

圖1 簡單模糊Bow-tie模型示意

Y1為事故事件，Y1左邊為T-S模糊故障樹，其中：X1～X3為基本事件，Y2為中間事件，M1與M2為T-S模糊門；右邊是以事故事件Y1為基礎，根據事故發生后可能產生的后果所建立的事件樹，其中：N1～N4為后果事件，B1和B2為安全屏障，YES與NO為安全屏障規則。

1.2 貝葉斯網絡

貝葉斯網絡是1種圖論與概率論相結合的賦值因果圖。給定根節點發生概率，無須求解割集，便可利用聯合概率分布直接計算葉節點的發生概率[10]。

1.3 模糊Bow-tie模型向貝葉斯網絡轉化方法

應用T-S模糊故障樹和事件樹分別轉化的方法將模糊Bow-tie模型轉化為貝葉斯網絡[11-12]。

具體轉化方法如下：

1)T-S模糊故障樹部分

將T-S模糊故障樹中的基本事件、中間事件和頂事件分別作為貝葉斯網絡中的根節點、中間節點和葉節點，當存在多個相同的事件時，在貝葉斯網絡中只需建立1個節點；用有向邊來連接貝葉斯網絡中對應的節點；利用T-S門規則對貝葉斯網絡中對應節點的條件概率表進行賦值。

2)事件樹部分

將事件樹中的安全屏障、事故后果分別作為貝葉斯網絡中的根節點、葉節點，兩者之間用有向邊進行連接，利用安全屏障規則對貝葉斯網絡中對應節點的條件概率表進行賦值。

其轉化流程框圖如圖2所示。

圖2 基于模糊Bow-tie模型構造貝葉斯網絡流程

2 構建輸氣管道泄漏燃爆FBT-BN模型

2.1 建立模糊Bow-tie模型

以西南某輸氣管道高后果區為例，從人的不安全行為出發，對風險源進行辨識，得出基本事件見表1，建立起以輸氣管道泄漏為事故事件的T-S模糊故障樹；再以輸氣管道泄漏事件為基礎，根據常見事故后果，用不同事故發生的觸發條件替代安全屏障，建立起燃爆事件樹，最終構建出輸氣管道泄漏燃爆模糊Bow-tie模型，如圖3所示。

表1 基本事件符號及描述

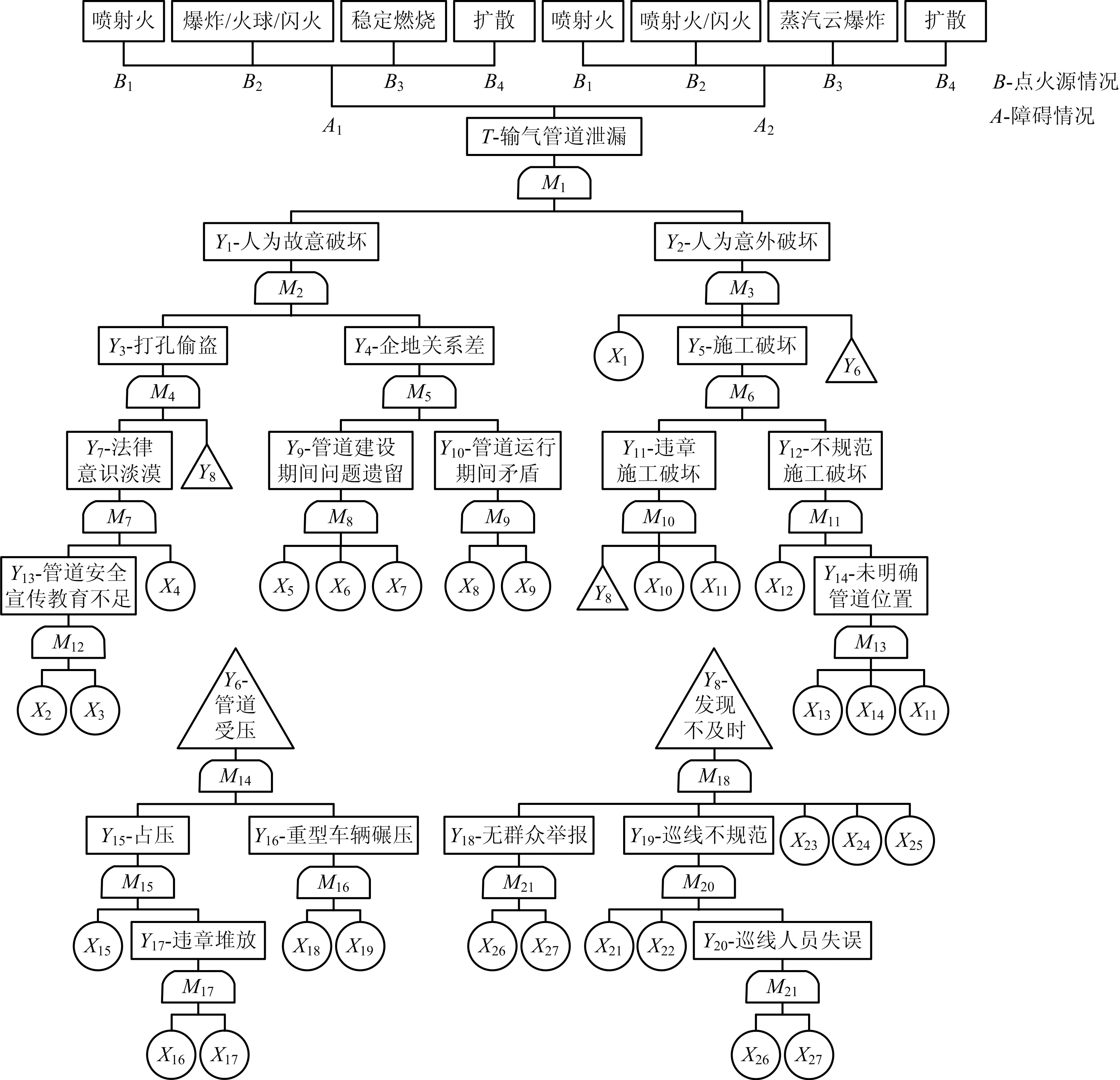
圖3 輸氣管道泄漏燃爆模糊Bow-tie模型

其中：T為頂事件，M1～M21為T-S模糊門，X1～X27為基本事件，Y1～Y20為中間事件，A1～A2與B1～B4為規則，分別為：A1(有障礙限制擴散),A2(無障礙限制擴散),B1(立即點燃),B2(當地延遲點燃),B3(遠距離延遲點燃),B4(無點火源)。

2.2 基于模糊Bow-tie模型構建貝葉斯網絡

在GeNIe軟件中繪制輸氣管道泄漏燃爆貝葉斯網絡，如圖4所示。

圖4 輸氣管道泄漏燃爆貝葉斯網絡

將圖3中事件樹所述的噴射火、閃燃、蒸氣云爆炸、火球統一視為燃爆事故，即N有3個狀態(燃爆/泄漏/無)，A具有2個狀態(有障礙限制擴散/無障礙限制擴散)，B具有4個狀態(立即點燃/當地延遲點燃/遠距離延遲點燃/無點火源)。

2.3 基于高后果區等級的人口敏感等級劃分

依據《油氣輸送管道完整性管理規范》[13]中對高后果區的描述，將其按人的不安全行為發生的可能性定義為不同等級人口敏感區，人口敏感等級劃分見表2。

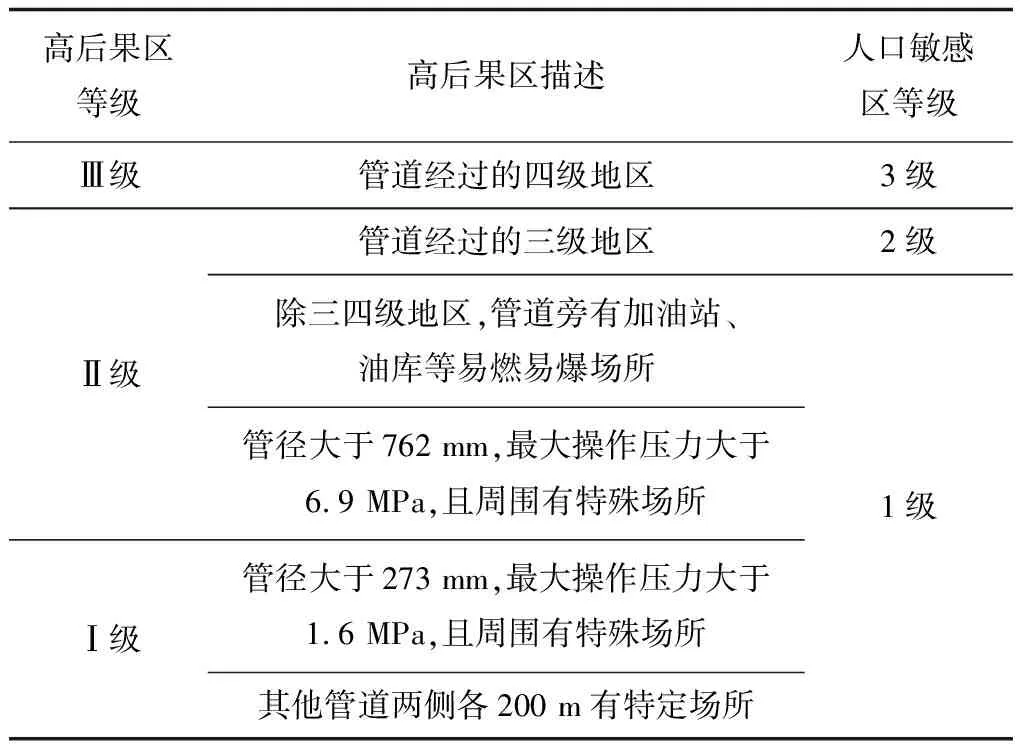
表2 人口敏感等級劃分

2.4 根節點先驗概率的確定

由于無法基于統計得到基本事件的發生概率，采用專家經驗評判法確定基本事件的發生概率。

以基本事件X1為例，經評判，基本事件X1在3級人口敏感區發生的可能性為高，依據事件發生概率評分準則，見表3[14]，得出發生概率評分等級為7，對應的概率值為0.025。因此在貝葉斯網絡中，根節點X1在3級人口敏感區的先驗概率為(0.025,0.975)。同理，可得到不同等級人口敏感區各根節點的先驗概率，各根節點先驗概率分布見表4。

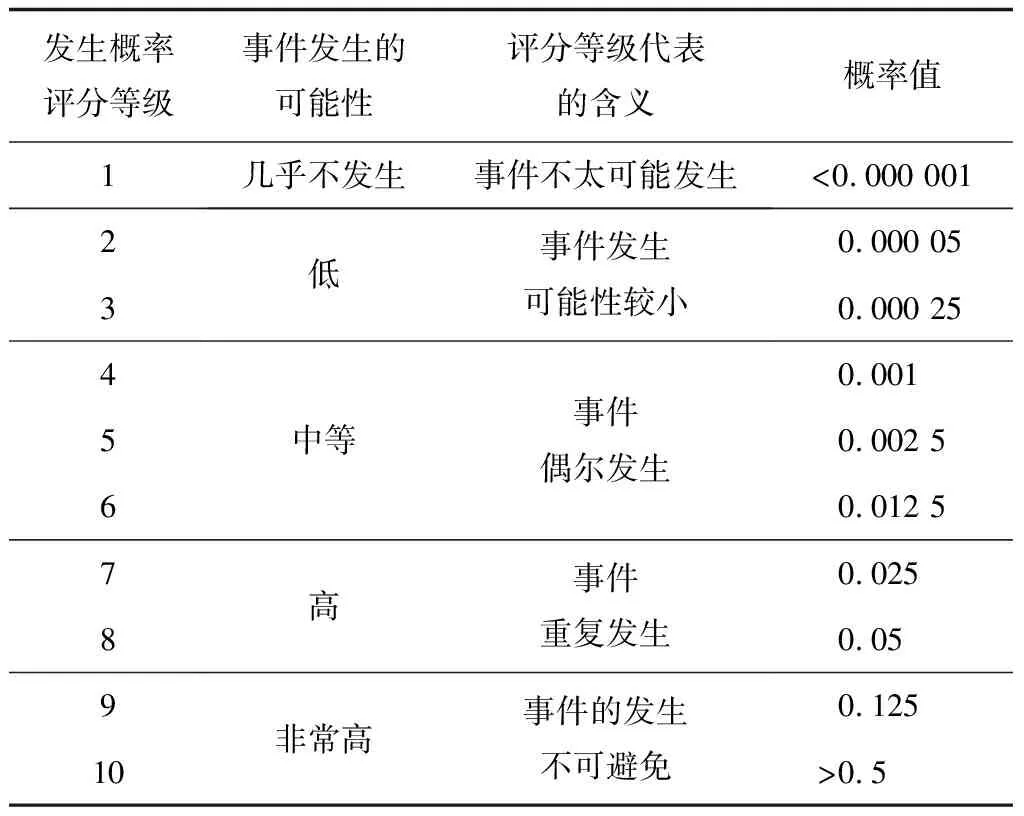
表3 事件發生概率評分準則

表4 根節點先驗概率分布

2.5 中間節點條件概率表的確定

以中間節點Y2為例，Y2有X1,Y5,Y63個父節點，若按傳統故障樹中或門的邏輯，當X1,Y5,Y6中任一事件發生，Y2均會發生；但在實際情況中，X1和Y6的發生可能并不會導致Y2的發生，因此需要結合實際情況和T-S模糊門對中間事件條件概率表進行賦值，傳統故障樹和T-S模糊故障樹2種方法下Y2的條件概率表見表5。

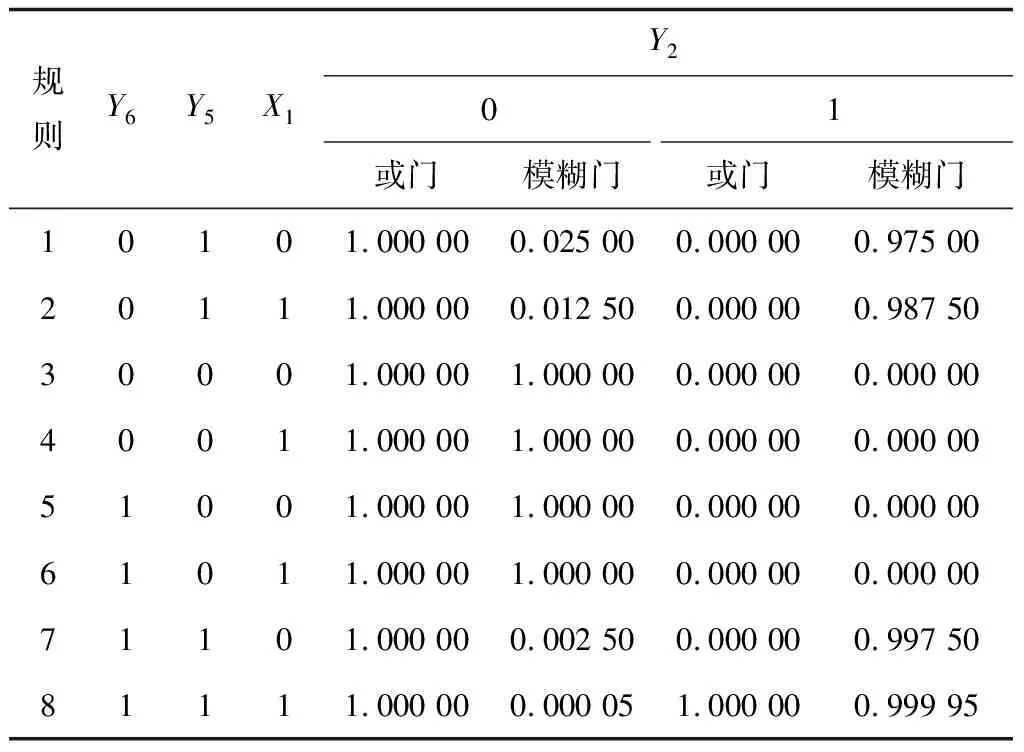
表5 2種方法下Y2的條件概率表

規則1表示：在Y6狀態為0，Y5狀態為1，X1狀態為0的條件下，Y2為狀態0的可能性為0.025、為狀態1的可能性為0.975，其他規則以此類推。

3 結果分析

3.1 泄漏燃爆事故易發性分析

通過貝葉斯網絡進行正向推理計算，得到不同等級人口敏感區泄漏燃爆事故發生的概率，見表6。不同等級人口敏感區泄漏燃爆事故概率對比如圖5所示。

表6 不同等級人口敏感區不同事故發生概率

圖5 不同等級人口敏感區泄漏燃爆事故概率對比

可以看出，隨著地區人口敏感等級的提高，輸氣管道泄漏和燃爆事故發生的概率均隨之增大，且燃爆事故發生的概率遠小于泄漏事故發生的概率。

3.2 泄漏燃爆事故致因分析

3.2.1 基本事件后驗概率分布分析

令P(N1)=1，通過貝葉斯網絡進行反向推理計算，得到導致在3個等級人口敏感區發生輸氣管道燃爆事故的各根節點后驗概率分布，見表7。輸氣管道泄漏燃爆各根節點后驗概率分布對比如圖6所示。

表7 根節點后驗概率分布

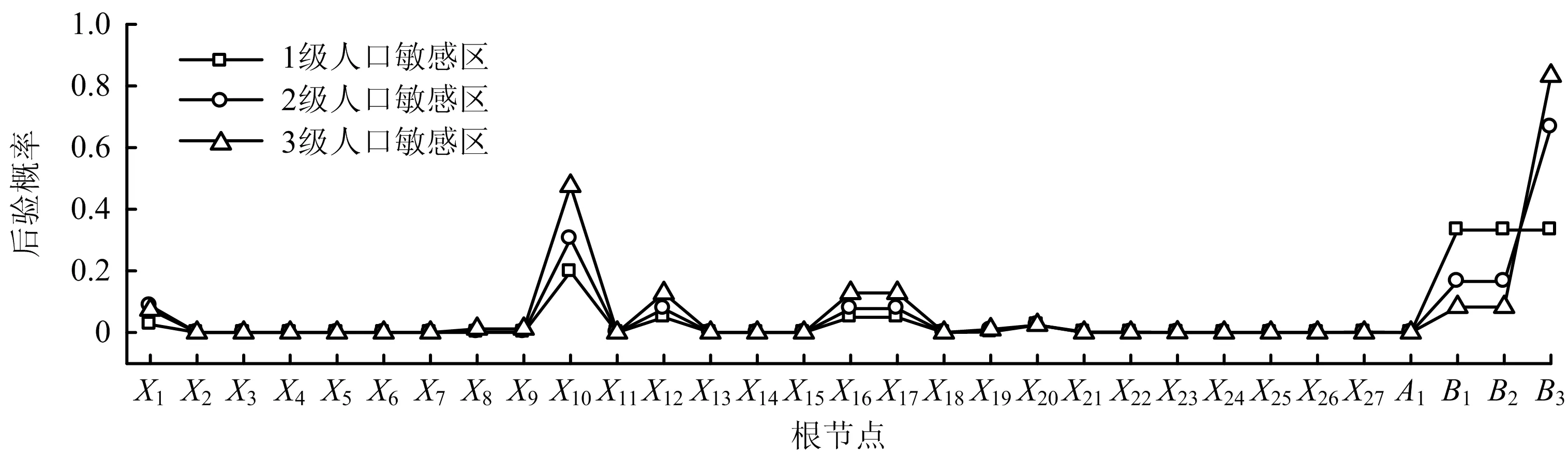
圖6 輸氣管道泄漏燃爆各根節點后驗概率分布對比

由圖6可知：

1)不同等級人口敏感區中，相同根節點的后驗概率存在差異。

2)在基本事件中，發生可能性最大的前幾項為：X10,X12,X16,X17,X1。其中，X10,X12位居前2位，X10發生的可能性遠大于其他基本事件。

3)在不同事故發生的觸發條件中，變化最為明顯的為B3，隨著地區人口敏感等級的提高，遠距離延遲點火發生的可能性增大。

3.2.2 靈敏性和影響力分析

為找出復雜致因結構中的重要參數以及導致事故發生的最可能途徑[15]，對貝葉斯網絡進行靈敏性和影響力分析。

1)靈敏度分析：3個等級人口敏感區的基本事件靈敏度大體一致，靈敏度較高的節點為X10,X12,X17,X16,X19,X15,X1，可以發現輸氣管道對非設計載荷較為敏感。

2)影響力分析：3個等級人口敏感區輸氣管道發生泄漏可能途徑一致，可能性排序靠前的2條為：X12→Y12→Y5→Y2→T與X10→Y11→Y5→Y2→T。

3.2.3 小結

經后驗概率分布、靈敏度、影響力分析，識別出風險性較大的基本事件為X10,X12，得到導致輸氣管道泄漏事故發生可能性最大的路線是由于施工破壞引起的管道泄漏，進而由遠距離延遲點火導致燃爆事故發生。分析所得管道泄漏事故主要致因與EGIG對近40 a 1 366起管道事故分析所得結果基本相符，驗證了所用方法的可行性。

4 結論

1)建立輸氣管道高后果區泄漏燃爆模糊Bow-tie模型并轉化為貝葉斯網絡，對不同等級人口敏感區泄漏燃爆事故易發性和事故致因進行分析。

2)隨著地區人口敏感等級的提高，輸氣管道泄漏和燃爆事故發生的概率隨之增大，燃爆事故發生的概率遠小于泄漏事故；導致輸氣管道泄漏燃爆事故發生可能性最大的途徑為：由于施工行為不規范和違章施工導致施工破壞，進而由遠距離延遲點火導致燃爆事故發生。

3)在無輸氣管道高后果區失效數據的情況下，分析結果與EGIG對近40 a 1366起管道事故所分析的結果基本相符，這驗證了該方法的可行性，但若有管道失效數據的支撐，可以采用統計所得概率與專家經驗評判所得概率相結合的方法，計算得到的結果會更加精準。