基于SPH方法的埋地PE燃氣管道挖掘破壞數值模擬研究

唐宇峰,史君林，李 濤

(1.四川輕化工大學 機械工程學院,四川 宜賓 644000；2.過程裝備與控制工程四川省高校重點實驗室，四川 宜賓 644000)

0 引言

隨城鎮化快速發展，諸如道路施工、地基開挖、基礎夯土等第3方作用導致埋地管道損傷或破壞事故屢見不鮮，造成嚴重經濟損失。其中，挖掘破壞導致管道損傷與破壞事故最為嚴重，且比例最大。目前，針對第3方挖掘造成管道破壞研究方法主要為有限元法：藍朝遜等[1]將管道破壞分為接觸、屈服、挖裂和挖穿4個階段，并采用有限元法分析管道彎頭在不同階段力學響應；李軍等[2]采用有限元分析基于應力與應變2種失效準則在管道失效過程中適用性；周立國等[3]采用ABAQUS分析挖掘載荷作用下燃氣管道力學特征及動力響應；Neacsa[4]模擬分析不同挖掘及影響因素對管道損失影響。在挖掘作用下，管道受土體、斗齒等多方面綜合作用力，出現裂紋擴展或破壞大變形，而基于網格的有限元法研究大變形問題時會產生網格畸變，即使采用網格重構技術，也存在計算費用昂貴，精度低甚至計算終止等問題。

光滑粒子流體動力學(Smoothed Particle Hydrodynamics,SPH)是1種新型純拉格朗日無網格計算方法，在諸如流體、巖土、爆炸與沖擊等計算力學領域得到廣泛應用[5-11]，粒子間無網格連接，避免因大變形導致的網格畸變，以表征大變形過程實時運動狀態。但在許多領域SPH仍處于起步階段，尤其在挖齒-土體-管道等多方接觸或沖擊作用等領域。因此，本文基于SPH理論，建立挖齒-土體-管道間相互接觸和沖擊力學模型，分析土體和管道在挖齒作用下動態響應。研究結果可為挖齒-土體-管道等多方接觸或沖擊領域研究提供新的計算方法。

1 SPH理論基礎及沖擊方程離散

1.1 SPH理論基礎

SPH法關鍵步驟為對任意宏觀變量函數f(x)的積分近似[12]，以及對連續積分表達式的粒子近似。任意宏觀變量函數f(x)的積分近似如式(1)所示：

(1)

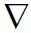
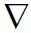
(2)

連續積分表達式的粒子近似是將相關連續積分表達式轉化為支持域內所有與粒子疊加求和的離散化方程，如式(3)所示：

(3)

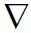
(4)

在式(1)～(4)中，光滑函數Wij的選擇對離散近似起重要作用。本文選取3次光滑核函數，如式(5)所示：

(5)

式中：R為點x和x′處2粒子間相對距離，R=r/h=|x-x′|/h，h為光滑長度，m；αd在1，2，3維空間下分別等于1/h，15/7πh2，3/2πh3。

1.2 基于彈性及彈塑性動力學理論的沖擊方程SPH離散

基于SPH基本理論，對質量守恒方程、動量守恒方程離散得到SPH形式下連續性方程及動量方程，如式(6)～(7)所示：

(6)

(7)

式中：vi與vj分別表示粒子i與j速度，m/s；α，β代表坐標方向；σαβ為總應力張量，N；Fα表示外力引起加速度，如重力、齒輪齒條相互作用力及固壁邊界作用力等;∏ij為人工黏度[13]，防止粒子接近發生非物理穿透，如式(8)所示：

(8)

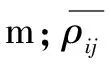
(9)

(10)

(11)

(12)

vij=vi-vj

(13)

xij=xi-xj

(14)

式中：vij代表粒子i與粒子j速度差，m/s；xij代表粒子i與粒子j距離,m。

同時，引入XSPH速度平均方法，如式(15)所示：

(15)

式中：ε為修正因子，取0.3。

PE管道為具有黏彈性的聚合物，其彈性模量隨時間增長而減少。由于挖齒與管道沖擊速度極快，可忽略時間影響，將模型簡化為分段彈性模型。對于土體模型，采用基于D-P屈服準則的彈塑性本構模型，如式(16)～(17)所示：

(16)

(17)

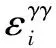
(18)

(19)

2 挖齒-土體-管道接觸模型

定義挖齒、土體、管道為不同部件。其中，挖齒作為剛體不考慮其變形，土體假設為連續均勻彈塑性介質，管體因受力時間短而假設為分段彈性介質。在SPH方法中，粒子一般通過核估計計算相互作用，如果不額外定義特殊接觸特性，當各部件相互分離時，接觸面處粒子將產生與實際情況不符的剪切及拉伸力。因此，本文作以下3個假設：1)將土體、管體內部視為連續體，挖齒-土體-管道接觸面處視為離散體。2)當接觸面處不同部件粒子間距為各部件粒子平均間距1/2時，部件間粒子視為相互接觸。3)當部件間粒子接觸時，給部件間粒子施加1個具有彈簧特性的相互作用力，該力與各部件變形及彈性模量有關，絕對值隨接觸粒子間距離減小而增大，且施加給各部件作用力大小相等，方向相反。當部件間粒子間距大于部件粒子平均間距1/2時，表示部件未接觸，即作用力為0；當部件接觸時，該力在2維條件下如式(20)所示：

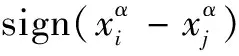
(20)

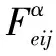
基于SPH采用FORTRAN編制埋地燃氣管道挖掘破壞數值模擬程序。其中，密度采用連續密度法求解，粒子信息更新采用跳蛙法，計算流程如圖1所示。

圖1 基于SPH的埋地燃氣管道挖掘破壞分析計算流程

3 數值算例

本文以挖齒挖掘薄層土覆蓋管道為研究對象，管道外徑0.104 m，壁厚0.008 m，土體長1 m，高0.24 m，挖齒截面為扇形，圓心角35°。挖齒視為剛體，并以1 m/s速度垂直向下運動；土體彈性模量20 MPa，泊松比0.25，黏聚力12.38 KPa，摩擦角20°；管體彈性模量1.115 GPa，泊松比0.3。模型共離散為1 986個粒子，其中土粒子1 262個，初始間距0.017 m；管粒子480個，初始間距0.005 m；挖齒粒子110個，初始間距0.01 m；邊界粒子132個，初始間距0.012 5 m。時間步長4×10-7s，共計算8×105個時間步，即0.32 s。PE管道塑性階段應力應變見表1。挖齒-土體-管道模型初始狀態如圖2所示。模型分別在0.208，0.288，0.32 s發生接觸、挖裂和挖穿，模型發生接觸、挖裂、挖穿時粒子分布如圖3所示。

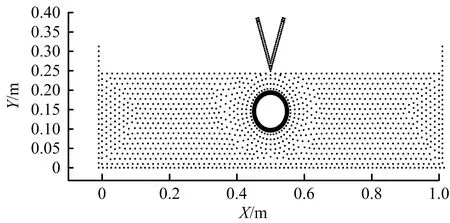
圖2 挖齒-土體-管道模型粒子初始狀態

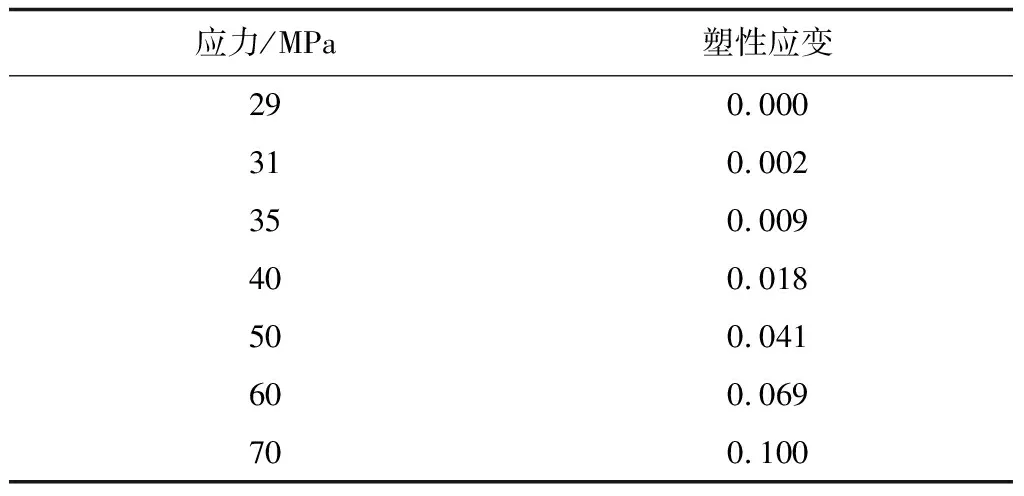
表1 PE管塑性階段應力應變

由圖3可知，SPH法可呈現挖掘過程挖齒-土體-管道實時動態及破壞狀態。在挖齒直接接觸管道前，管道變形較小；當挖齒直接作用管道后，管道以接觸點為中心產生較大變形直至斷裂。

圖3 模型發生接觸、挖裂、挖穿時粒子分布

進一步采用橢圓度對管道變形定量評價，如式(21)所示：

(21)

式中：Dmax、Dmin分別為管道最大外徑與最小外徑，m。挖齒挖掘土體及管道全過程，管道橢圓度隨挖掘時間變化關系如圖4所示。

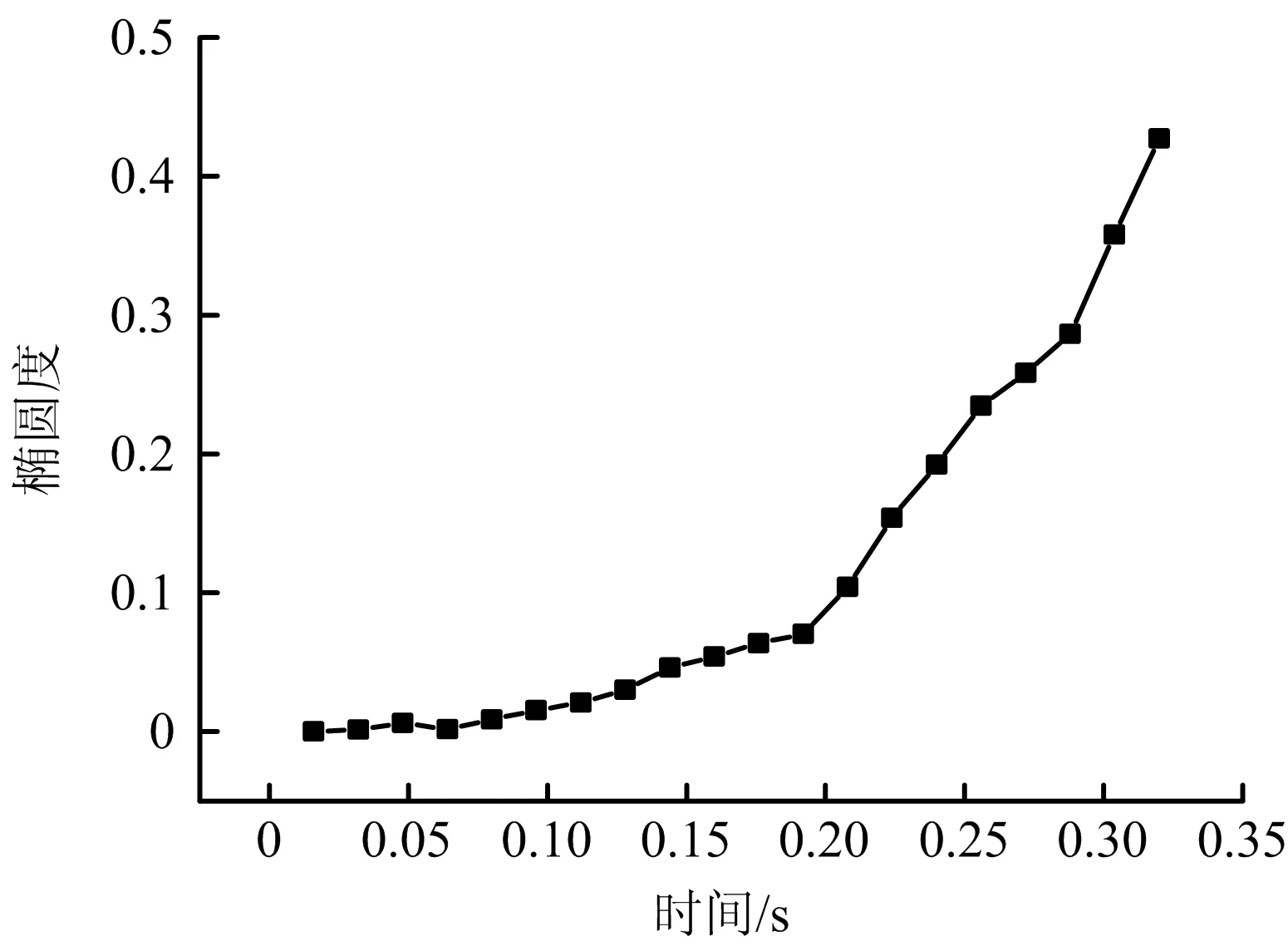
圖4 管道橢圓度隨挖掘時間變化關系

由圖4可知，盡管在0.208 s前挖齒尚未直接接觸管道，但部分挖齒作用力由土體傳遞給管道，仍會使管道產生一定橢圓度變化，但此時橢圓度不足0.1，不會對管道產生破壞；當挖齒與管道直接接觸后，管道橢圓度迅速增大并且逐漸挖裂，挖裂后管道抵抗變形能力大幅降低，直至挖穿時橢圓度約為0.45。

各挖掘階段管道環向應力及環向應變分布如圖5～6所示。由圖5～6可知，管道環向應力隨挖齒向下作用而逐漸增大，管道由接觸至挖穿過程中，最大應力應變發生在挖齒與管道接觸部分，即管道正上方；當管道發生挖裂時，最大應力約35 MPa，等效應變約0.045；當管道挖穿時，環向應力約65 MPa，等效應變約0.08。此外，當管道貫通后，管道上方約45°位置會出現較大應力應變，易發生進一步破壞。

圖5 各挖掘階段管道環向應力分布

圖6 各挖掘階段管道環向應變分布

采用有限元法對相同模型模擬，以驗證SPH法準確性。但有限元法挖裂后網格趨于畸變，因此，以挖裂初環向應力為例進行對比，如圖7所示。有限元方法在挖裂階段得到環向最大應力約35 MPa，與SPH法結果一致。

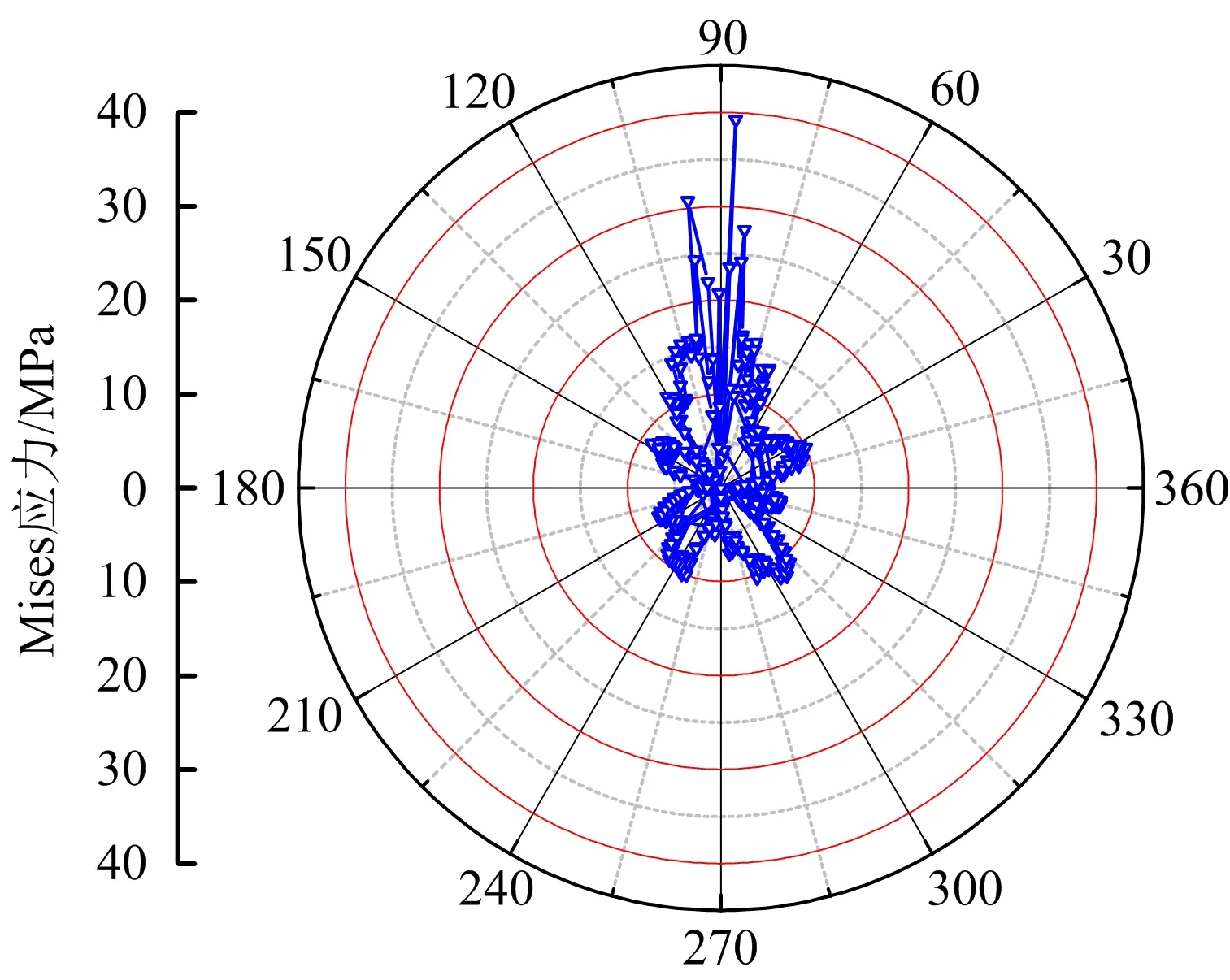
圖7 挖裂階段管道環向應力分布(有限元)

4 結論

1)當挖齒作用于土體而尚未作用于管道時，管道橢圓度受一定影響，但不會產生斷裂或破壞；當挖齒直接作用于管道且繼續向管道方向挖掘時，管道會發生局部斷裂直至挖穿。

2)挖齒與管道直接接觸點為管道發生破壞或斷裂第1危險點；當管道繼續大變形后，其左右兩側受拉力作用可能產生斷裂破壞，為斷裂第2危險點。

3)模型離散粒子數量及計算域等相關因素對計算精度產生一定影響。