隔聲量的阻抗管法和混響室法仿真計算對比
張 苗,漆瓊芳,李英偉
(1.武漢第二船舶設計研究所,武漢430000;2.渤海造船廠集團有限公司,遼寧葫蘆島125004)
在船舶、軌道交通、建筑等行業經常出現噪聲污染,因此所使用的壁板一般具有一定的隔聲性能,隔聲量是隔聲構件的一項重要指標,是指材料一側的入射與另一側的透射的聲功率級差,目前對隔聲量的估算主要采用等效質量法和質量定律等,隔聲量測試可采用駐波管和混響室法[1–2]。
目前,劉冬冰[3]根據垂直入射阻抗管傳遞函數法、四傳聲器法編寫了吸聲系數和隔聲量計算程序,并將隔聲量理論值和數值仿真結果進行對比,驗證了所設計的斜入射隔聲阻抗管的設計可行性。董明磊[4]分析混響室隔聲量的測試原理,并推導了三傳聲器法、四傳聲器法及改變邊界的四傳聲器法的隔聲量計算公式,設計了隔聲量數據處理儀器,計算仿真值與儀器測量值吻合較好。趙陽[5]基于四傳聲器阻抗法原理,引入聲源反射系數和吸聲末端的反射系數,推導了考慮反射修正的試件隔聲量公式,采用北京聲望阻抗管進行測試得到4個傳聲器通道的復聲壓,根據提出的修正公式對傳遞損失進行修正,將試件解析解與修正值進行對比,驗證了所提出的隔聲量修正公式的準確性。石嘉欣、楊德慶等[6]采用有限元法模擬駐波管,并與混響室模型和瑞利李茲法進行比較,確定了駐波管模型的邊界條件。劉杰等和張樹峰[7–8]采用FEM 法的AML 技術模擬無反射邊界,并定義結構-內聲場-外聲場的耦合面,對隔聲罩進行聲-振耦合計算。
本文分別基于駐波管和混響室法建立了試件隔聲量仿真模型,通過建立試件結構域與周圍空氣域的聲-振耦合模型,施加無反射邊界模擬消聲室,采用隨機聲場模擬無指向性聲源等方法,得到聲-振耦合計算的測點聲壓值,并根據后處理公式編程得到試件隔聲量,探討了試件邊界條件、夾層、聲波入射形式等參數對隔聲量的影響。
1 聲學模型理論方法
1.1 聲學有限元
聲學有限元的原理是將求解域劃分成一系列單元,單元之間由節點相連,引入插值函數用以描述單元變量,依據變分及加權余量等建立聲學有限元方程,根據聲壓、阻抗、質點振速等邊界條件求取節點變量,從而得到節點處變量的近似數值解。
理想流體介質中聲壓的波動方程為
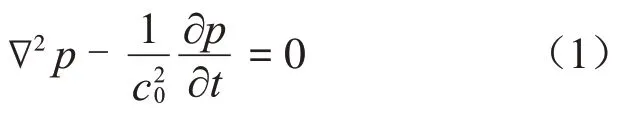
式(1)解的形式為p2(x,t)=f(ωt-kx)+g(ωt+kx),其中:x是位移,t是時間,ω是聲波角頻率,波數k=2πf/c,f是頻率(Hz),c是聲速(m/s),管中聲速c=343.2,T為空氣溫度(K),p是管道內聲壓(Pa)。式(1)中,c0是聲速,p是聲壓。
聲學有限元中采用插值函數:

其中:{N}是節點聲壓列向量,{p}是形函數列向量。
根據格林函數將式(1)轉化為
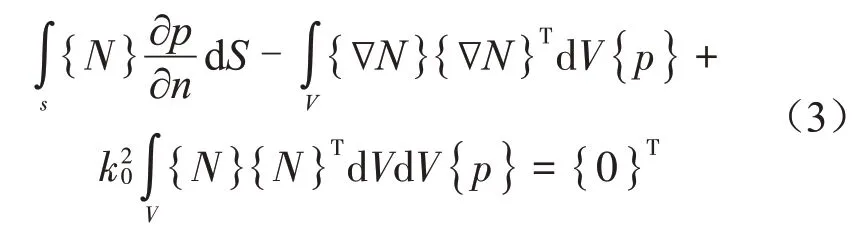
其中:?n是結構外法向,邊界表面S=Sr +Sv +Sz,Sr、Sv、Sz分別是剛性壁面表面、法向質點振速表面和法向聲阻抗表面,一般定義3種聲學邊界條件。
剛性壁面邊界條件為

法向質點振速un的邊界條件為
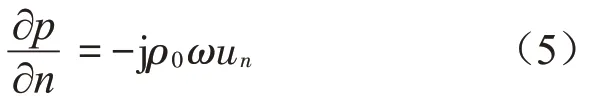
法向聲阻抗z的邊界條件為
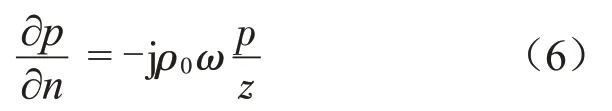
根據聲學邊界條件,得到等式:
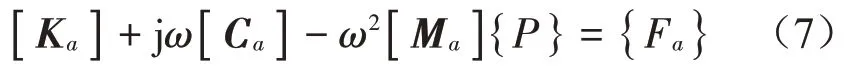
1.2 四傳聲器的阻抗管法
隔聲量測試所用阻抗管如圖1 所示,發聲管內的揚聲器近似發出平面波聲源,假設發聲室的正向波為PA,反向波為PB,接受管內的正向波為PC,反向波為PD,傳聲器1#、2#、3#、4#與試件近端面的距離分別為x1、x2、x3、x4,傳聲器測點聲壓分別為P1、P2、P3、P4,接受管端部有吸聲的聲學末端。
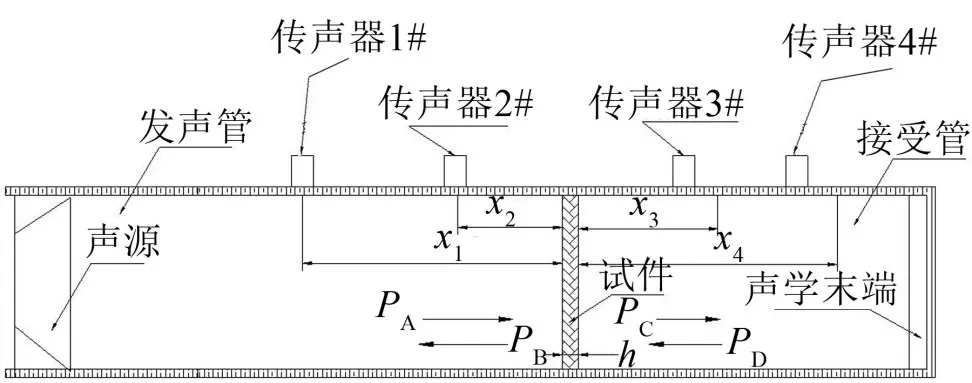
圖1 隔聲量測試用阻抗管
根據四傳聲器法,發聲管和接收管內傳聲器1#、2#、3#、4#的復聲壓分別為
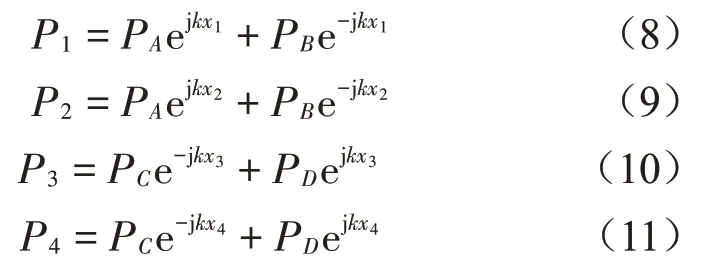
其中:波數k=2πf/c,f是計算頻率(Hz),c=343.2是管中聲波的速度(m/s),T是空氣溫度(K)。
試件的透射系數τp為
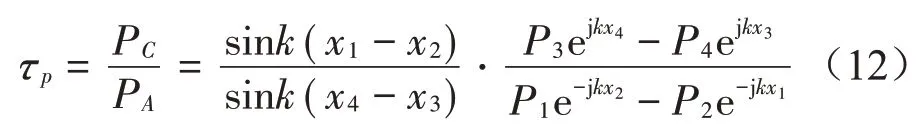
試件的傳遞損失TL為
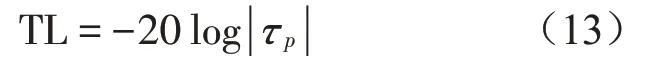
四傳聲器法忽略聲波多次反射,只考慮聲學末端的一次反射,因此聲學末端的吸聲越佳,測量結果越精確。
1.3 混響室法
隔聲量測試所用的混響室一般如圖2 所示,在發聲室(混響室)布置無指向性聲源用于發射聲波,發聲室的壁面反射較高,可將發聲室的聲場視作擴散聲場。在接收室(消聲室)四周布置吸聲尖劈等,可將接收室內的聲場視作自由聲場。試件安裝在發聲室和接受室中間墻面的孔洞上,可認為發聲室的聲波無規則入射到試件上。
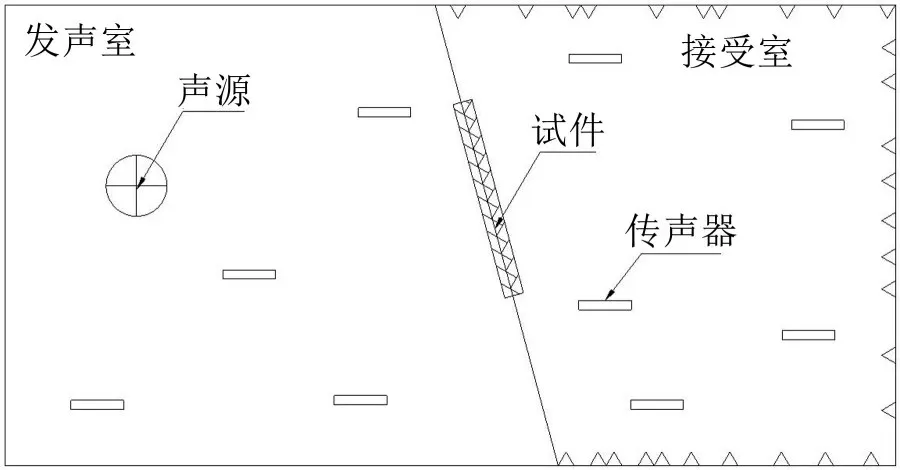
圖2 隔聲量測試用混響室
試件的入射聲功率Win為
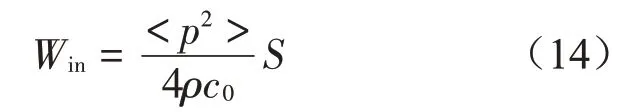
其中:
因此試件的入射功率Win為

其中:pa為入射聲腔的聲壓幅值。
透射聲功率Wt與總聲強I和試件表面積滿足:

傳遞損失TL為
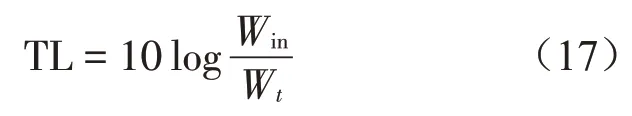
仿真時根據式(15)計算出入射聲功率,提取試件與接受室的耦合聲功率即透射聲功率,通過式(17)得到試件的傳遞損失,稱之為隔聲構件的隔聲量。
1.4 隔聲量曲線質量定律
假如聲波以θ角斜入射,根據質量定律,單層板隔聲量公式[2]為
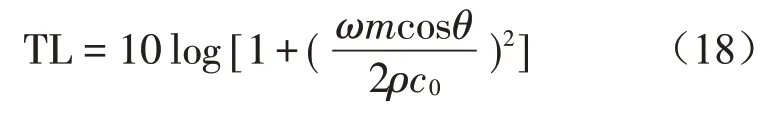
其中:m是單位面積質量(kg/m2),ω是圓頻率,f是頻率(Hz),ρ是空氣密度(kg/m3);c0是聲速(m/s)。
若聲波垂直試件入射,傳遞損失TL1為
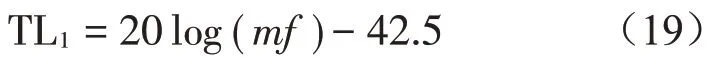
若聲波隨機入射,傳遞損失TL2為

在測試或仿真時板隔聲量曲線可能出現V型低谷,這是由于板彎曲波波長等于入射波波長在板方向的投影時,兩波產生共振造成隔聲量下降,該現象稱為吻合效應,最低吻合頻率稱為臨界頻率[2]。比共振頻率低的頻段稱為剛度控制區,比共振區高的頻段進入質量控制區,共振頻率估算公式如下:
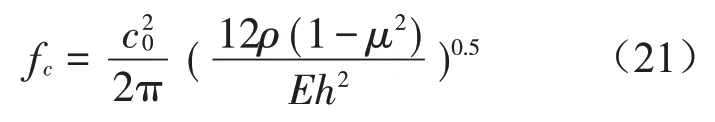
其中:c0是聲速,θ是聲波入射角,E是材料彈性模量,μ是材料泊松比,h是板厚。
2 建立聲學模型
2.1 聲學計算模型的建立
2.1.1 阻抗管模擬法
如圖3 所示,阻抗管內徑為100 mm,發聲管長480 mm,接收管長580 mm。建立試件的結構有限元以及阻抗管內空氣域的聲學有限元,單元尺寸為10 mm,為保證每個單元尺寸至少大于等于6個聲波長,計算頻率范圍取為5 Hz~4 000 Hz。在發聲管初始端施加速度載荷,模擬揚聲器的平面波聲源,聲波垂直入射到試件上,在接收管端部施加無反射邊界條件,模擬聲學末端,根據四傳感器法的距離關系設置傳聲器測點,采用Virtual. Lab Acoustic 軟件進行直接聲-振耦合計算,提取傳聲器測點的復聲壓,再根據四傳聲器法公式即式(8)至式(13)進行后處理,采用MATLAB編程計算試件在垂直入射波作用下的傳遞損失。
2.1.2 混響室模擬法
如圖4 所示,采用混響室模擬法時的試件尺寸與阻抗管模擬法一致,在試件左右兩邊建立空氣域有限元模型,模擬混響室里的發聲室和接受室,基于試件結構域與兩側空氣域分別建立聲-振耦合面,在接受室非聲-振耦合面設置聲波向外輻射而無反射邊界,模擬半消聲室的自由場。在試件發聲室一側設置12 個隨機平面波聲源,用于模擬混響聲源,聲波非垂直無規則入射到試件上,也可設置平面波聲源,模擬聲波垂直入射在試件上。
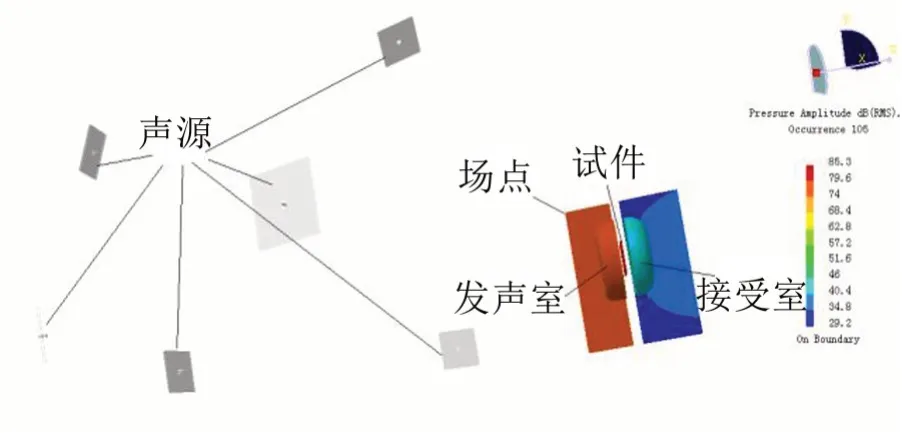
圖4 隔聲量計算的混響室模擬法
采用Virtual. Lab Acoustic 進行直接聲-振耦合計算及隨機聲場計算,根據12個平面波工況的耦合響應合成隨機計算的響應,分別提取試件與發聲室耦合面的聲功率和試件與接收室耦合面的聲功率,根據式(14)~式(17)計算試件的在無規則入射波作用下的傳遞損失。
2.1.3 聲學模型的有效性驗證
對比聲波在無限介質中垂直入射中間層的理論隔聲量公式計算結果、文獻測試值[3]與本文阻抗管法模擬的結果。其中,本文阻抗管模擬法所采用的試件為鋁板,彈性模量為70 GPa,泊松比為0.3,密度為2 700 kg/m3,厚度為10 mm,對試件結構不施加約束,網格尺寸為10 mm,在發繩室一側施加1 m/s 速度激勵模擬平面波聲源的垂直入射。文獻[3]中采用自主設計的阻抗管,管壁厚10 mm,測試13 種試件的隔聲量,所選擇試件6 為2 mm 鋁板,與本文阻抗管試件一致。得到隔聲對比曲線如圖5所示。
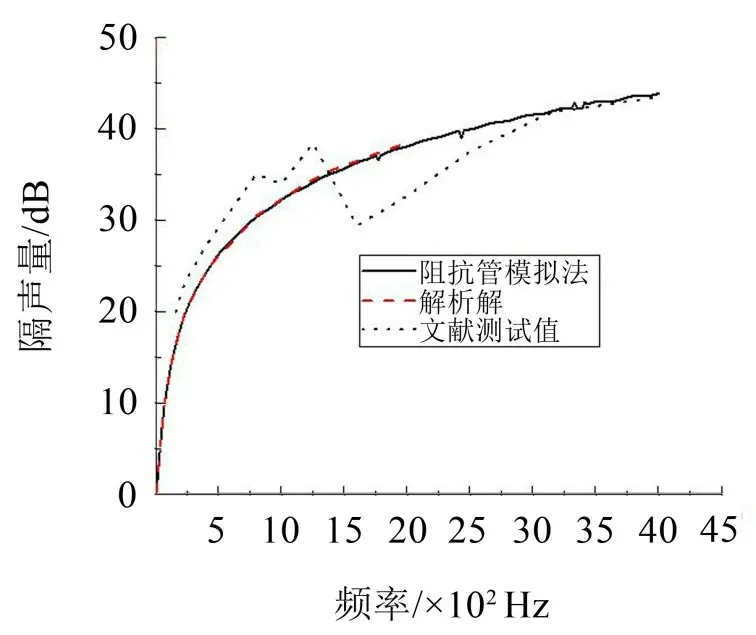
圖5 隔聲量仿真的有效性驗證
在5 Hz~2 kHz范圍內,阻抗管模擬法的結果和解析解接近。在300 Hz~4 kHz 范圍內,仿真值、解析解和實驗值較為接近。測試值在1 600 Hz 有低谷,這可能與測試時試件的安裝狀態有關,不同邊界條件影響了試件安裝模態,造成在某些固有頻率下產生隔聲低谷。3種方法所得的隔聲量曲線在趨勢上較接近,說明阻抗管四傳聲器模擬法是仿真計算隔聲量的一種有效方法,驗證了根據式(8)至式(13)編制的隔聲量計算程序的準確性。仿真計算結果與測試值存在差別,這是因為試件并非理論上的無限大障板,試件的邊界條件、剛度、阻尼、吻合效應等會影響隔聲量測試結果。
對2.1.2 節中所述阻抗管內試件施加剛性固定約束,將平面波聲源入射到試件上。對2.1.3節所述混響室中的試件采用剛性固定約束,采用直徑2 500 mm 的半球形模擬發聲室和接受室,發聲室一側采用出至于試件的平面波模擬,發聲室和接受室的單元尺寸10 mm,在發聲室和接受室外側設置快速吸收AML模擬無反射邊界,使用混響室法仿真模型的混響室大小、網格密度、AML 均滿足25 00 Hz 計算頻率上限。在1/3倍頻程10 Hz~2 500 Hz范圍內的隔聲量曲線如圖6所示,曲線變化趨勢較為一致。
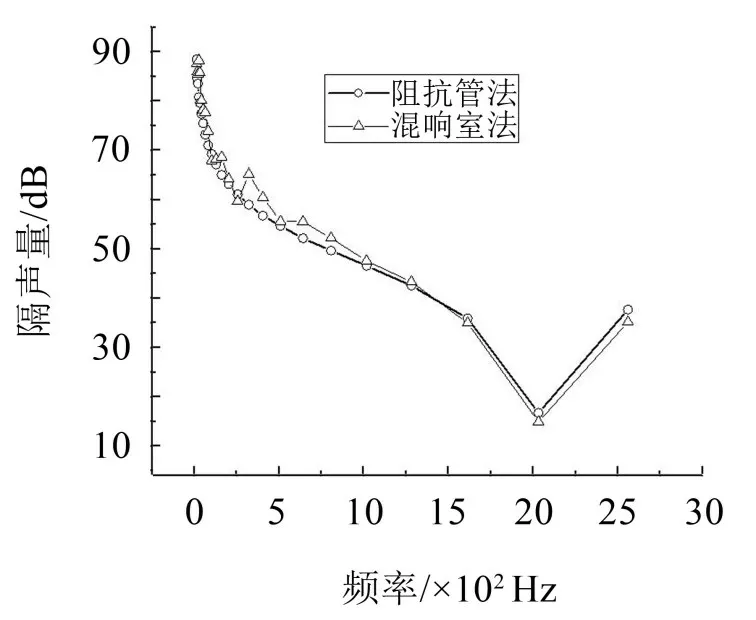
圖6 混響室法和阻抗管法所得隔聲量對比
3 模型參數對結果影響分析
3.1 試件邊界條件對隔聲量的影響
以阻抗管模型為例,鋁板直徑為100 mm,厚為2 mm,設置鋁板3 種類型的邊界條件,分別為自由、簡支和剛性固定,隔聲量計算結果如圖7所示,在計算頻率5 Hz~4 kHz范圍內,試件在自由狀態下時其計算結果與文獻測試值[3]較為接近。當頻率增加至大于2 500 Hz 時,試件在簡支和剛性固定邊界下的隔聲量曲線較為接近。當試件剛性固定時,隔聲量曲線有明顯的峰值和低谷,曲線呈現震蕩現象。當試件處于自由邊界狀態時,隔聲量曲線較平緩無明顯震蕩現象。總結以上現象可知試件邊界約束越強,隔聲量曲線上下震蕩越明顯,在低頻階段,試件邊界約束越強,隔聲量偏大,這是因為在低頻階段,隔聲量處于剛度控制區,仿真時若對試件施加剛性約束則試件剛度增加,在低頻剛度控制區域剛度越大則隔聲量越大。在自由狀態下仿真時,試件尺寸較大時,可認為其尺寸近似于半無限尺寸,這種情況下與質量定律下的聲傳播特性較為一致。實際工程應用中,試件幾乎不能達到完全剛性、完全簡支或完全自由狀態,因此進行隔聲量仿真計算時,建議采用自由邊界條件,得到的曲線較為平緩且呈現出質量控制區特性,在全頻段與測試值較為接近。隨著頻率的繼續上升,試件進入質量控制區,隔聲量主要與試件面密度有關,所以3 種邊界條件下仿真結果較接近。試件隔聲低谷一般出現在結構的共振頻率附近,試件模態與約束邊界條件有關,試件所受約束為簡支時,1 kHz 左右出現隔聲低谷,試件所受約束為剛性支撐時,2 kHz 左右出現隔聲低谷,試件邊界約束越強,試件剛度越大,隔聲低谷越向高頻移動。
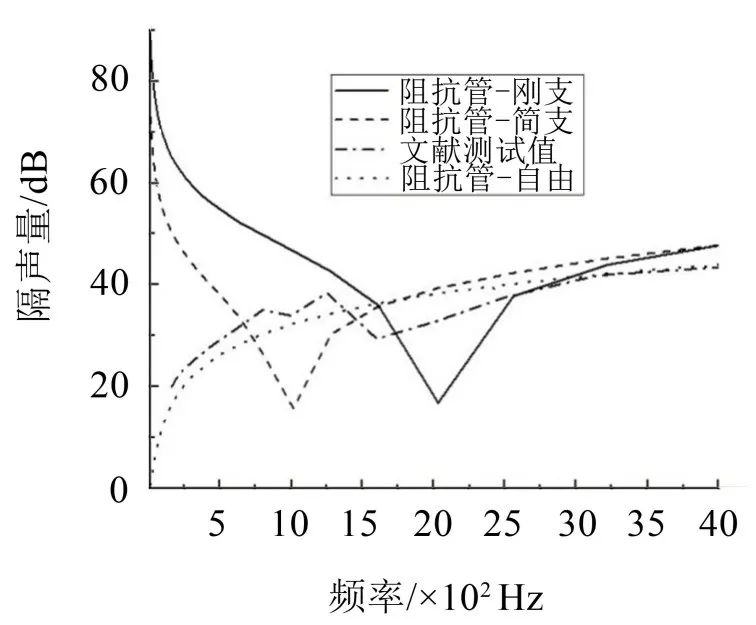
圖7 不同邊界條件對隔聲量的影響
3.2 夾層對試件隔聲量的影響
根據混響室模型,取公路兩側聲屏障常用的PMMA 板為研究對象。假設試件尺寸為0.9 m×1.2 m,彈性模量為53.5 GPa,泊松比為0.35,密度為1 180 kg/m3,試件分別為:試件1(10 mm PMMA板)、試件2(5 mm PMMA 板+60 mm 空氣層+5 mm PMMA 板)、試件3(5 mm PMMA 板+100 mm 空氣層+5 mm PMMA板)。網格尺寸小于最大計算頻率的1/6,網格密度能滿足最大計算頻率為2 000 Hz的要求,但由于使用了大范圍的自動匹配邊界層(AML)模擬無反射邊界,網格密度能滿足最大計算頻率為510 Hz 的要求,最終取計算頻率為5 Hz~510 Hz,得到隔聲量曲線如圖8 所示。可知當使用隨機聲源和空氣域時,采用聲-振計算所得的曲線震蕩比較大,并非呈現出文獻[2]中光滑的曲線,隨著夾心層厚度的增加,隔聲低谷有向低頻移動的趨勢。
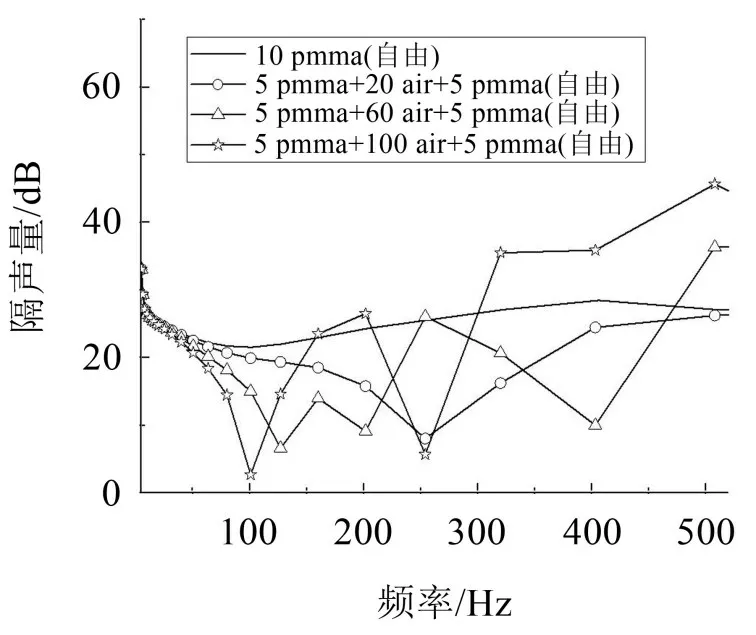
圖8 夾層厚度對試件隔聲量影響
3.3 無規則入射與垂直入射對隔聲量的影響
采用4.2節中所述的試件1為研究對象,設置自由邊界,分別采用平面波入射和混響聲源入射到試件上。
(1)無規則入射:發聲室內混響聲源無規則入射到試件上,設置試件結構網格與空氣域的耦合面,采用12 個隨機平面波聲源模擬12 面的無指向性聲源。
(2)垂直入射:發聲室內平面波垂直入射到試件上,設置試件結構域和空氣域的聲-振動耦合,采用一個沿試件法向的平面波模擬垂直入射。
根據兩種入射方式計算所得的隔聲量如圖8所示。當聲源為平面波垂直入射時或者隨機無規則入射時,隔聲量曲線如圖9 所示。在200 Hz 以上垂直入射相較無規則入射計算所得的隔聲量偏大,但在50 Hz~200 Hz范圍內偏小,與式(20)所反映的一般規律有所不同,有可能與采用聲學有限元計算時發生的曲線震蕩有關。
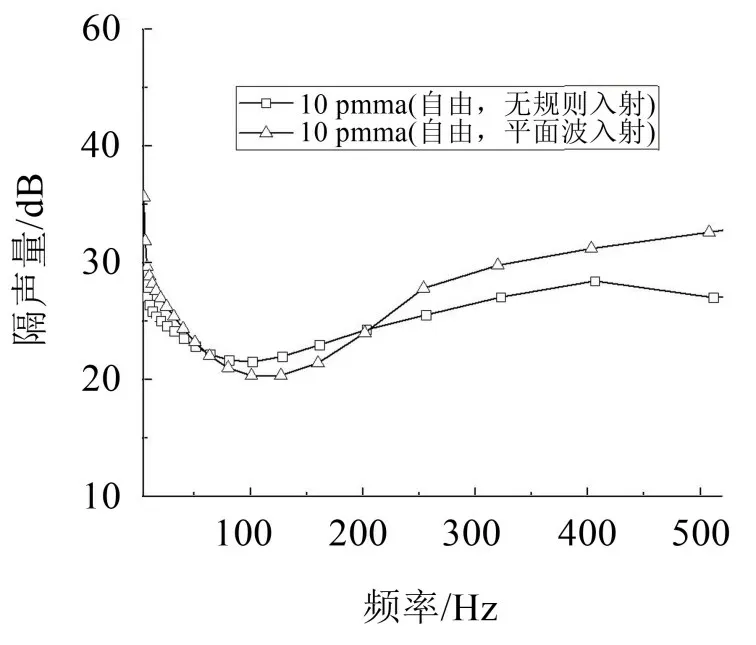
圖9 垂直入射與無規則入射聲源對隔聲量計算的影響
4 結語
根據測試隔聲量的四傳聲器阻抗管法和混響室法,建立兩種聲學計算模型,通過隨機混響聲源模擬、設置無反射邊界、設置聲振耦合以及四傳聲器法編程等處理過程,得到隔聲量計算的兩種方法,對比邊界條件、夾層參數、聲波入射形式等,總結如下:
(1)進行隔聲量仿真計算時,可采用四傳聲器阻抗管模擬法和混響室模擬法,阻抗管模擬法計算效率較高,但需提取傳聲器復聲壓并采用后處理公式編程進行隔聲量計算。混響室模擬法計算時間成本較大,但隔聲量曲線的后處理過程較為便捷。
(2)若研究隔聲材料在全頻段的隔聲量數值大小,而非重點關注隔聲量曲線的頻譜特性,則進行隔聲量仿真時建議采用自由邊界條件,得到的隔聲量曲線較為平緩,無明顯震蕩現象且呈現質量控制區特性,在全頻段與測試值較為接近。
(3)試件邊界約束越強,在低頻段剛度控制區仿真隔聲量越大,實際工程應用中試件不可能完全無約束,若仿真隔聲量時采用自由邊界,在較低頻段的剛度控制區域內隔聲量偏小,但在其他較寬頻段內與測試值較為接近。
(4)采用混響室模擬法可模擬發聲室內的混響聲源和垂直試件的平面波聲源,而阻抗管模擬法僅適用于平面波聲源。
(5)混響室模擬法由于采用AML 屬性模擬無反射邊界,會使模型計算頻率在上升到某頻率值時失效,故適用于較低頻,且曲線上下震蕩較大。同樣網格密度的條件下,阻抗管模擬法可適用于更高頻率。

