基于支持向量回歸的煤粉工業鍋爐煙氣氧含量預測

楊 晉 芳

(1.煤科院節能技術有限公司，北京 100013； 2.煤炭資源高效開采與潔凈利用國家重點實驗室，北京 100013；3.國家能源煤炭高效利用與節能減排技術裝備重點實驗室，北京 100013)

0 引 言

煤粉工業鍋爐是近十年來發展起來的1種新型工業鍋爐，以其高效、節能、環保等優點代替鏈條爐并迅速進入市場。煙氣氧含量是燃煤鍋爐的重要指標之一[1]，其對鍋爐的效率和排放有著重要的影響[2-3]，很多學者致力于鍋爐氧含量優化的相關研究[4-6]。

目前煤粉工業鍋爐煙氣氧含量的測量主要通過直接測量方式，借助氧化鋯傳感器或熱磁式傳感器測量煙氣氧含量[7]，以上儀器可直接顯示氧含量的百分比，其反應速度快、測量精度較高，然而也存在以下3個問題:① 價格成本高；② 氧化鋯探頭在長期使用中會被粉塵堵塞而出現老化現象，嚴重影響儀器的穩定性和準確性；③ 氧量儀還需定期進行效驗。因此，此次研究考慮采用間接測量技術對煙氣氧含量進行檢測。

間接測量采用軟測量的方法[8],即利用易于測量的一些輔助變量以估計主要變量,已在電站鍋爐上推廣應用并取得較好的效果。采用軟測量方法間接獲得煙氣氧含量，可與儀器測量值比較并對其進行修正，同時可實現對氧含量的實時監控，從而提高鍋爐的燃燒效率[9]。

軟測量的建模方法主要分為以下4種[10]，分別基于工藝機理分析方法、模式識別方法、人工神經網絡方法和支持向量機方法。基于工藝機理分析方法存在滯后，很難符合實際工業現場對監測數據實時性的需求；基于模式識別方法通常與人工神經網絡和支持向量機等方法相結合，并應用至實際生產中；基于人工神經網絡方法易形成局部極小而得不到全局最優，很多學者針對此項缺點對其進行改進。基于回歸支持向量機方法應用于回歸估計問題中，得到很好的效果，此方法預測精度很高且泛化能力強。目前已有較多基于此方法進行軟測量模型的建立，并已應用至工程實際。但該方法對于大規模訓練樣本難以實施，建模精度不高。至目前為止，最常用的軟測量方法主要包括基于人工神經網絡和支持向量機的方法。

針對基于人工神經網絡和支持向量機方法的煙氣氧含量間接預測技術，已有大量研究并成功應用于電站鍋爐。胡世廣[11]利用神經網絡進行火電廠煙氣含氧量的測量并進行建模研究，為火電廠的氧量測量技術提供新手段。馬良玉[12]等基于L-M算法改進神經網絡模型以更準確地預測煙氣含氧量,為實現鍋爐的燃燒優化調整、節煤降耗奠定基礎。Zhenghao Tang[13]等使用DBN深度學習模型對電廠鍋爐氧含量進行預測，結果顯示可準確地預測結果。Ma Liangyu[14]等基于ANN對1000MW電廠煙氣氧含量進行預測，結果顯示此模型可精確預測煙氣氧含量，對電廠改善鍋爐燃燒、節約能源和減少煤耗具有指導作用。楊秀等[15]采用1種基于粒子群改進的支持向量機算法對氧含量軟測量進行建模研究，仿真結果表明預測精度較高、泛化能力良好。任錦等[16]提出改進最小二乘支持向量機模型PSO-LSSVM并對氧含量進行預測，最終仿真結果顯示:改進的軟測量模型預測精度更高且泛化性更好、模型可靠性更高。Changliang Liu等[17]使用LS-SVM對煙氣氧含量進行預測，通過預測值和實際值比較可知，其提出的模型可較準確地預測電廠煙氣氧含量。

以上研究均針對電站鍋爐，而目前對煤粉工業鍋爐氧含量的預測仍很稀少，由此筆者提出煤粉工業鍋爐氧含量預測模型，以期為工業煤粉鍋爐燃燒系統優化提供指導。

1 現場數據采集

現場數據采集基于煤粉工業鍋爐系統的以下工藝流程:煤粉由供料器均勻送入鍋爐燃燒器并在爐膛內燃燒，煙氣經爐膛內的SNCR(Selective Non-Catalytic Reduction)選擇性非催化還原脫硝和尾部的SCR(Selective Catalytic Reduction)選擇性催化還原脫硝后，進入NGD(No Gap Desulfurization)半干法脫硫除塵一體化裝置進行脫硫除塵，潔凈煙氣排至煙囪進入大氣，鍋爐飛灰經倉泵輸送至密閉灰塔排出，經封閉罐車運輸出廠。

煤粉鍋爐DCS(Distributed Control System)分布式控制系統中的歷史數據是整個鍋爐工藝過程的所有設備測點數據，而氧含量的預測只與部分工藝相關，即進料、燃燒和煙氣排放3個過程，因此采集數據時只需篩選出關于3個過程的相關變量即可。

以某礦20 t/h煤粉工業鍋爐為研究對象，以20 min為采樣時間，采集了采暖高峰期2個月的數據。根據系統機理和工藝流程對變量進行初選，選擇了給料頻率、引風機頻率、爐膛負壓、前爐膛溫度、省煤器出口煙溫等20個變量。以上變量分為控制變量和狀態變量兩大類。控制變量為技術操作可控制的變量，采集的控制變量為6個，分別為給料頻率、補水閥開度、引風機頻率、二次風閥開度、進風閥1開度、進風閥2開度。狀態變量是反應鍋爐狀態的一些變量，不能直接控制，初篩包括狀態變量14個，分別為蒸汽流量、前爐膛溫度、后爐膛溫度、一次風壓、省煤器入口煙溫、省煤器入口水溫、省煤器出口煙溫、省煤器出口水溫、蒸汽壓力、二次風流量、爐膛負壓、蒸汽溫度、爐尾負壓、汽包水位。

2 數據預處理和變量篩選

2.1 數據預處理

從現場運行的歷史數據庫中所采集的數據一般情況下都含有異常數據及干擾數據，其會影響模型的訓練，因此需對歷史數據進行預處理[18]。此次研究刪除異常值和缺失值后，最終得到2 598條數據。

2.2 變量篩選

輸入的變量直接影響模型的預測準確性，太多的輸入變量將會降低預測精度并增加模型的計算時間，因此有必要將冗余數據去除。通過歷史數據集的相關性選擇，使用F檢驗判斷每個輸入變量和煙氣氧含量的關系。F檢驗、方差齊性檢驗是用來捕捉每個特征與標簽之間線性關系的過濾方法。使用F檢驗將篩選出與氧含量有著顯著關系的變量。通過以下公式(1)和公式(2)計算F值，F值越大則輸入變量與氧含量之間的相關性就越大。

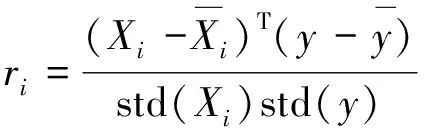
(1)

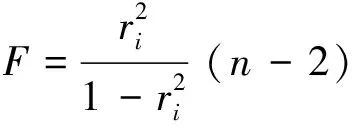
(2)

式中，Xi代表所有樣本在i號特征上取值的n維列向量，y是氧含量;ri是樣本的相關系數。

經過F檢驗，從上述20個變量中選取與氧含量關系顯著的變量:蒸汽流量、給料頻率、后爐膛溫度、一次風壓、二次風閥開度、進風閥1開度、進風閥2開度、省煤器入口煙溫、引風機頻率、蒸汽壓力、爐膛負壓、二次風流量、爐尾負壓、蒸汽溫度14個變量，其中控制變量5個，狀態變量9個。

2.3 數據標準化

從DCS中采集的歷史數據，其各變量有著不同的單位，一些變量大小在數值上相差很大，有的甚至達到幾個數量級。為了不影響模型的精度，需要將采集到的數據進行Z-score 標準化，以消除因為數據數量級相差大造成的變量對模型作用差異大。

Z-score標準化公式詳見如下公式(3):

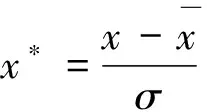
(3)

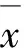
經過Z-score標準化的所有數據都聚集在0附近，方差為1，經過處理后的數據不會造成因數據的數量級差異而影響模型精度等問題。

3 建立模型

3.1 支持向量回歸(SVR)

支持向量機是用于分類的算法，支持向量也可用于回歸，稱之為支持向量回歸(SVR)。支持向量機可分為支持向量分類和支持向量回歸[19]，支持向量回歸因其優越的學習性能，使其在系統辨識、預測估計等領域被廣泛研究應用。文中預測氧含量值，采用支持向量回歸算法。

給定數據集:D={(x1,y1),(x2,y2),……,(xn,yn)},yn∈R，且令:

f(x)=wTx+b

(4)

w和b是待確定的模型參數，T為轉置符號，希望學得1個回歸模型,使得f(x)與y盡可能接近。假設能容忍f(x)與y之間最多有ε的偏差，如圖1所示。

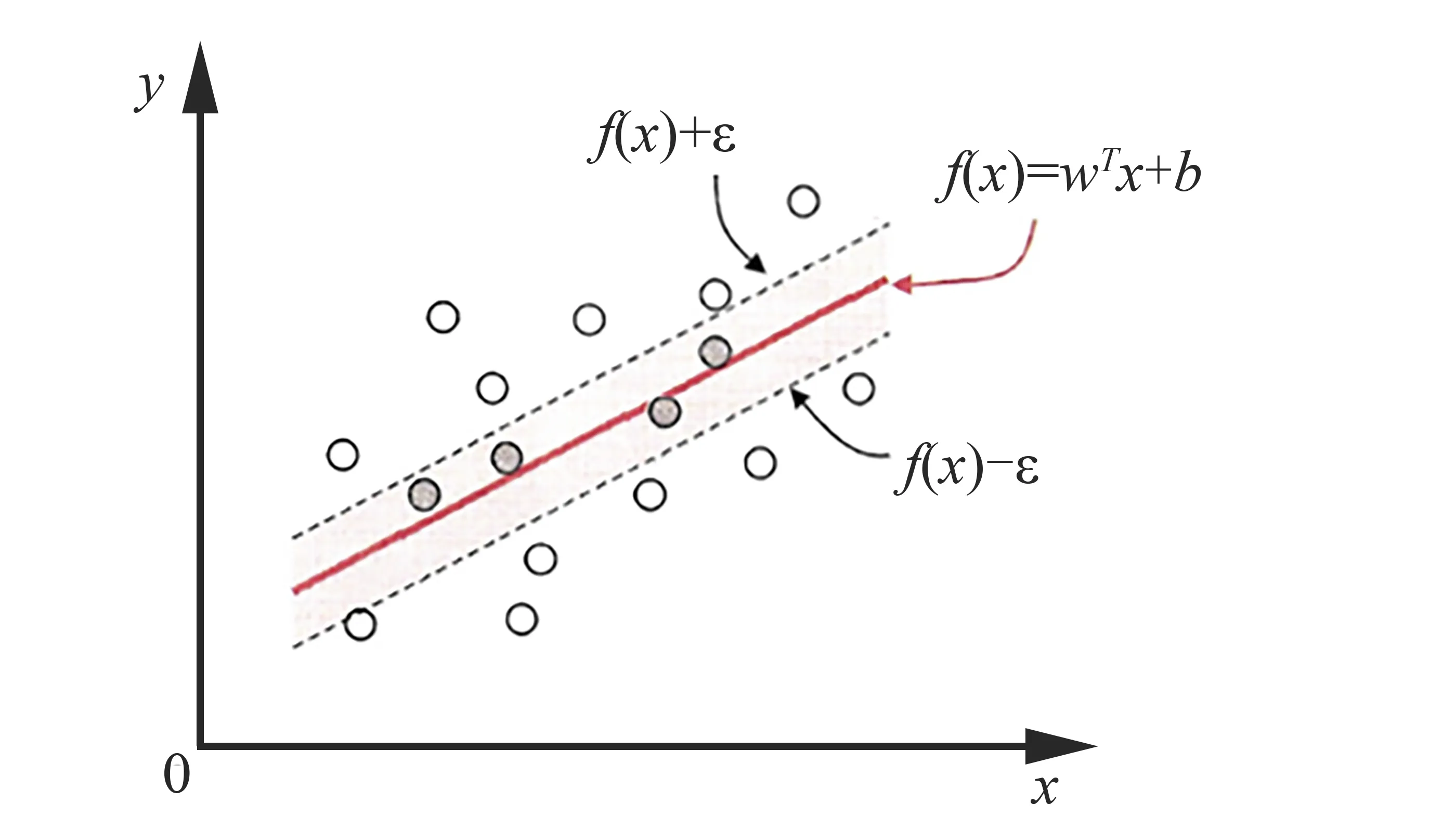
圖1 支持向量回歸模型原理圖Fig.1 Schematic diagram of support vector regression model

即僅當f(x)與y之間的差別絕對值大于ε時才計算損失。于是，SVR問題可形式化為:

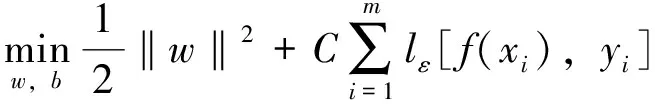
(5)

式中,C為正則化常數;lε是圖1中所示的ε-不敏感損失函數:

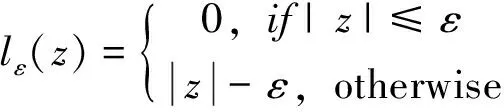
(6)

引入松弛變量和拉格朗日乘子，最終可解得SVR為:

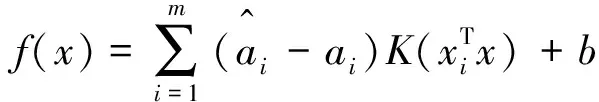
(7)

3.2 建立模型

上文經過F檢驗已篩選出14個變量，其中控制變量5個、狀態變量9個。模型中的變量見表1。考慮到輸入變量的性質，將模型訓練分為控制變量、狀態變量以及兩者合并3種方式，并分別對3個訓練的模型依次進行測試。

表1 模型中的變量詳情Table 1 Variables details in model

3.3 模型訓練與預測

將經過處理的2 598條數據的70%作為訓練集，建立控制變量、狀態變量以及兩者合并的支持向量回歸模型并進行訓練，30%作為測試集測試模型的性能。3種情況下煙氣氧含量軟測量模型的預測結果分別如圖2、圖3和圖4所示，藍色實線代表直接測量所得的真實值，桔色虛線代表預測值。

從圖2～圖4可看出，3種軟測量模型的煙氣氧含量預測值均能較為準確地反映真實值的變化趨勢。

將圖2與圖3和圖4分析比較可知，圖2預測值與真實值差距偏大，控制變量調節后可即時反饋到從DCS中取得的數據上，例如給料頻率從20調整為10，取得的歷史數據顯示為10，而實際鍋爐工況需要一定的時間才能基本穩定地運行在給料頻率為10的工況。因此若取到此組數據，瞬時取到的氧含量值有一定的誤差。故若只基于控制變量來預測模型，結果和直接測量之間的誤差較大。而基于狀態變量的預測結果符合最佳，出現以上現象是由于狀態變量較控制變量有一定的延遲，和直接測量得到的氧含量較為同步。對于基于控制變量和狀態變量兩者合并的SVR模型，其準確度介于兩者之間。

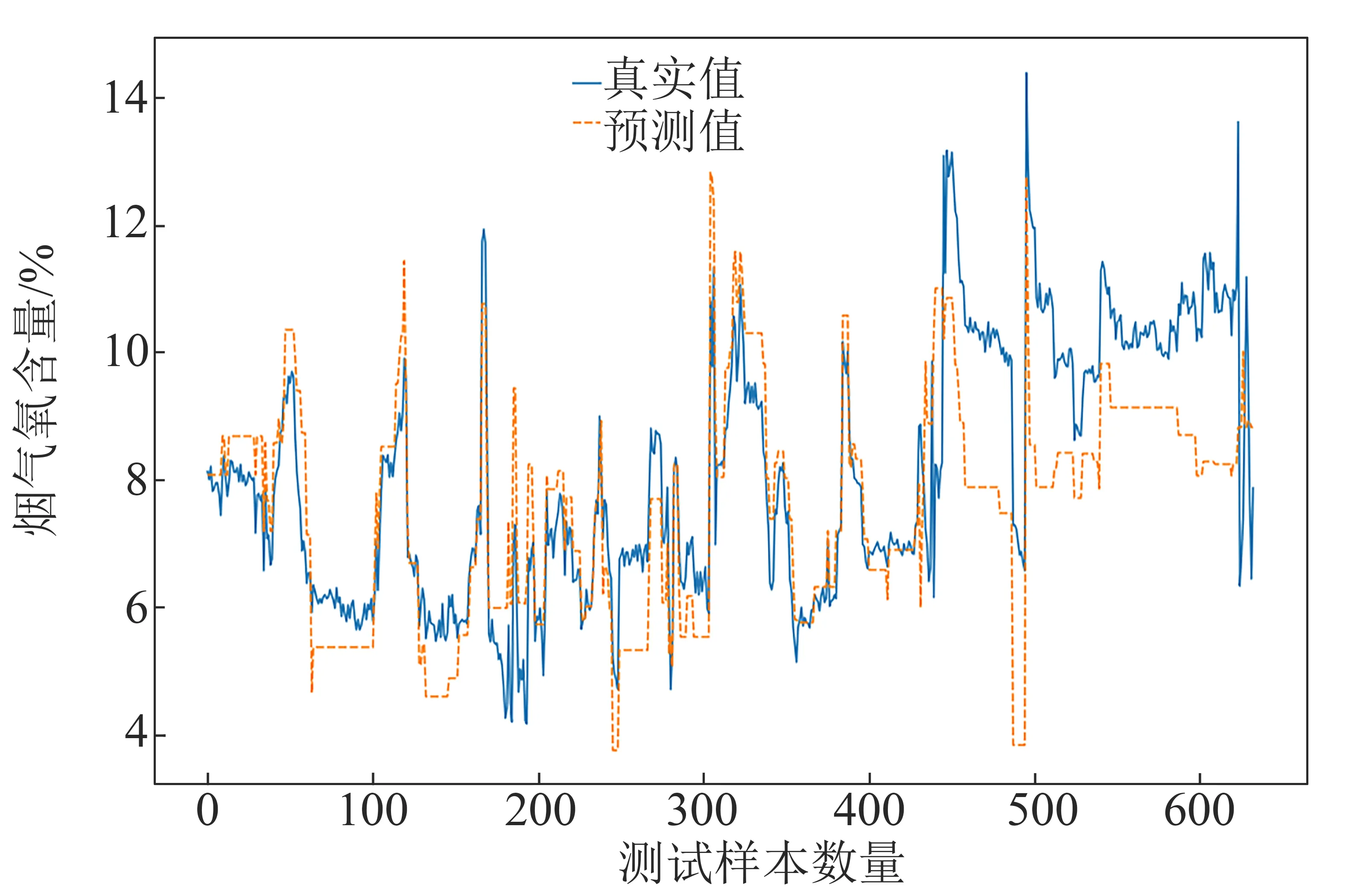
圖2 基于控制變量的預測值與真實值比較Fig.2 Comparison of prediction values and real values based on control variables

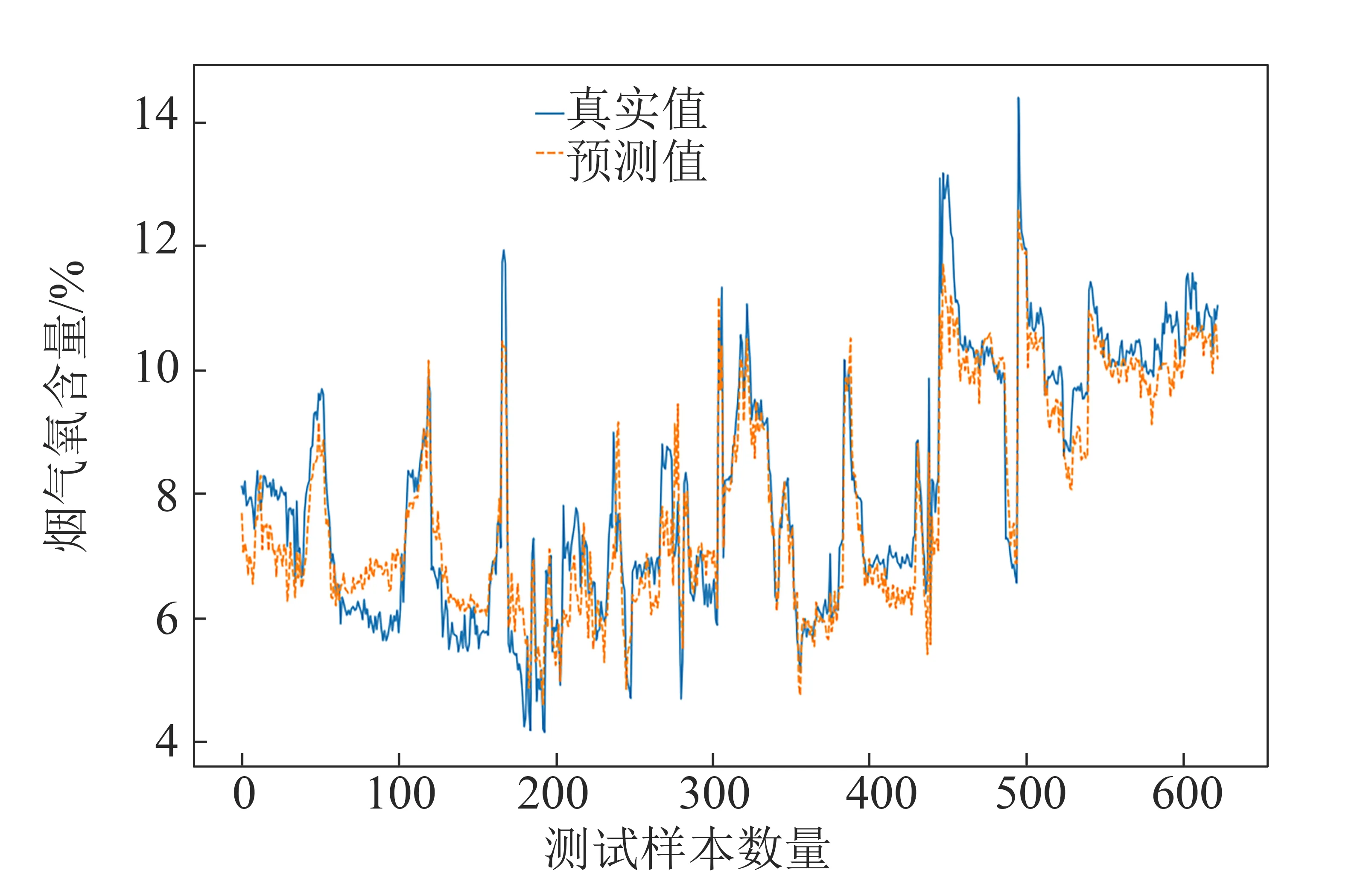
圖3 基于狀態變量的預測值與真實值比較Fig.3 Comparison of prediction values and real values based on state variables

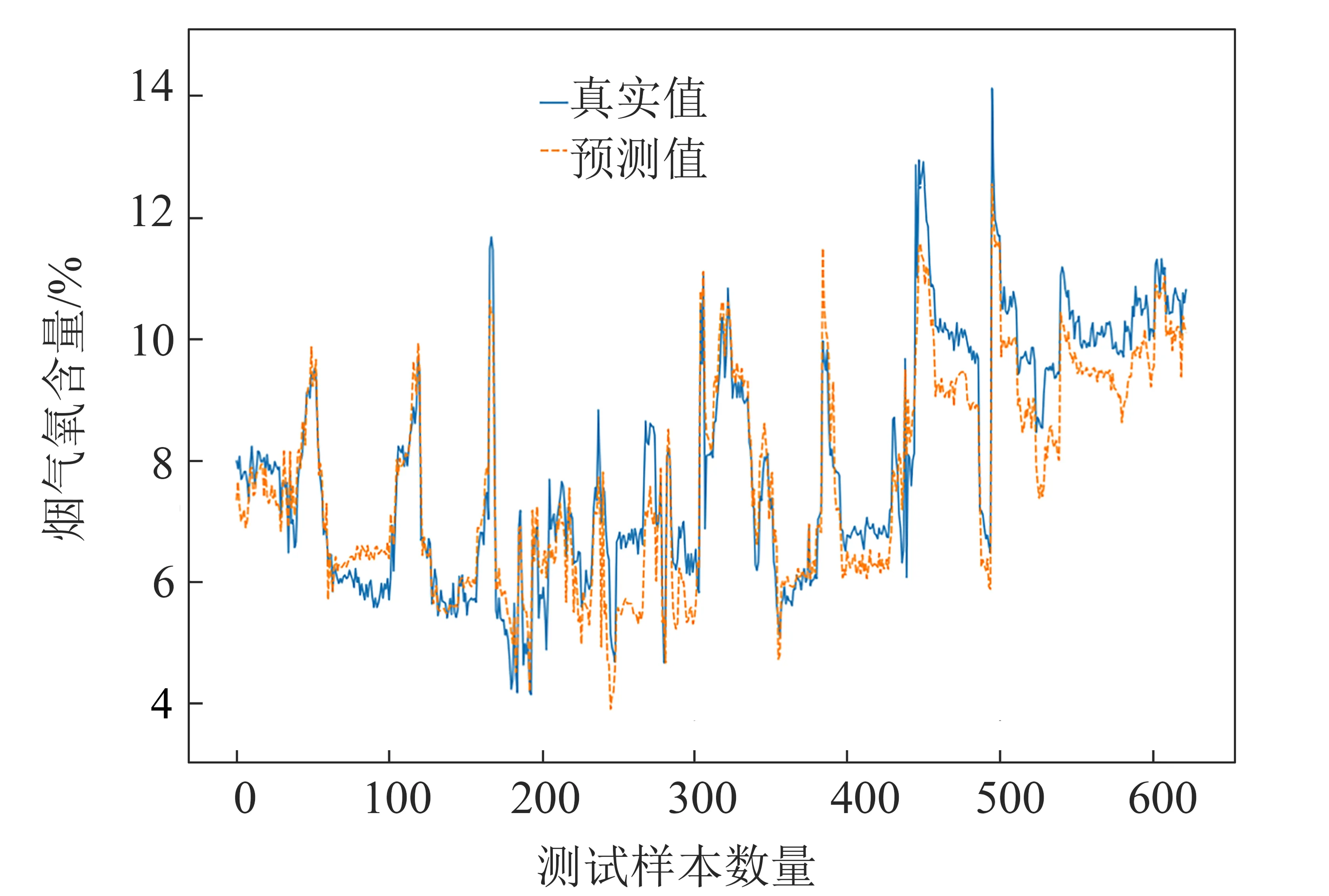
圖4 控制變量和狀態變量合并的預測值與真實值比較Fig.4 Comparison of prediction values and real values based on both control and state variables

3.4 模型評價

為了評價預測模型，使用均方誤差(MSE)、平均絕對誤差(MAE)和決定系數(R-Square)來衡量預測模型的性能[20]，其計算見公式(8)～公式(10):

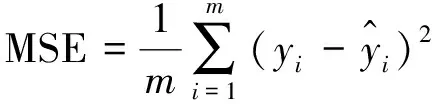
(8)

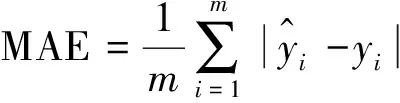
(9)

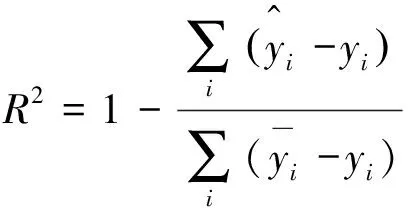
(10)

式中m——測試數據的樣本數量，個；

yi——煙氣氧含量真實值，%；

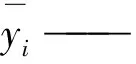
對測試結果分析詳見表2，MSE和MAE的值越小，說明模型精度越高。而R2取值范圍為[0,1]，R-Squared越大，表示模型擬合效果越好。評價指標進一步說明基于狀態變量的SVR模型效果最佳。

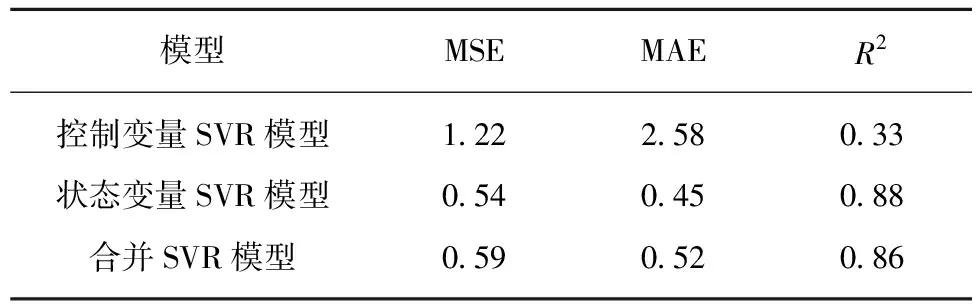
表2 模型評價指標Table 2 Model evaluation indicators

4 結 語

煤粉工業鍋爐的燃燒工況較為復雜，而直接測量氧含量儀器成本高，還受到鍋爐運行積灰等影響，因此軟測量越來越受到人們的重視，也逐漸應用至實際工業生產中。煙氣氧含量預測技術已在電站鍋爐上得以推廣應用，對在工業鍋爐上的應用具有借鑒意義。

為了解決工業鍋爐的氧含量軟測量問題，筆者提出了支持向量回歸模型對工業鍋爐的煙氣進行氧含量測量。整個預測模型分為以下3個部分:

(1)選取煙氣氧含量的主要影響變量并將其對應的數據標準化，使用了F檢驗篩選出對氧含量有顯著影響的變量，最終選取14個變量作為輸入，為了防止因不同的變量數值上數量級相差較大進而造成訓練模型時各變量作用相差巨大，對輸入數據進行Z-score標準化。

(2)建立模型。將第一步選出來的變量分為控制變量和狀態變量，并運用SVR理論構建分別基于控制變量、狀態變量和兩者合并的氧含量預測模型，結果表明3種模型的趨勢與測量值一致，基于狀態變量SVR模型優于其它兩者，基于狀態變量的模擬結果能較好地預測實際值的趨勢，為工業煤粉鍋爐燃燒系統優化提供指導。

(3)模型評價。為了評價預測模型，使用均方誤差、平均絕對誤差和決定系數來衡量預測模型的性能，進一步證明了基于狀態變量的SVR模型效果最佳。