用等濃度薄層移動法測量液相擴散系數
王瑞仙,錢春霖,王 艷,孟偉東,普小云
(云南大學 物理與天文學院,云南 昆明 650091)
液相擴散系數是研究傳質過程,計算傳質速率及化工設計與開發的重要基礎數據,廣泛應用于物理、化工、生物及醫學等領域中[1-4]. 膜池法、泰勒分散法和全息干涉法是測量液相擴散系數的3種傳統方法. 其中,膜池法所需操作時間長,而且需要對實驗系統進行膜池標定[5];泰勒分散法由于設備加工精度的限制導致其測量精度較低[6];全息干涉法測量精度高, 但對實驗裝置的穩定性要求高, 測量時間較長[7].
為解決上述存在的問題,李強等[8]基于玻璃毛細管對芯區溶液折射率的空間分辨測量能力,提出了用玻璃毛細管測量液相擴散系數的方法——等折射率薄層移動測量法. 該方法較好地解決了傳統測量方法存在的測量速度慢、抗環境干擾能力弱等問題,并具有樣品需要量少、測量速度快、系統穩定性好等特點[9-10]. 但在確定等折射率薄層位置時,推導并計算出液芯柱透鏡的焦距與芯區液體折射率的關系f(n);在確定等折射率薄層對應的溶液濃度時,用實驗方法測量并擬合出溶液的濃度與折射率[11]的對應關系C(n). 為簡化測量過程,進一步縮短測量時間和提高測量精度,本文基于消球差液芯柱透鏡搭建了光學測量體系,提出用等濃度薄層替代等折射率薄層的方法測量液相擴散系數. 無需計算f(n)和測量C(n) 關系,用等濃度薄層移動測量法即可測量液相的擴散系數. 本文采用該方法在室溫下(25.0 ℃)測量了葡萄糖水溶液的液相擴散系數,結果表明:此測量方法具有裝置和操作簡單、結果可靠、擴散過程可視化等特點,是利用基礎光學知識和基本光學元器件測量液相擴散系數的有效方法.
1 實驗原理
1.1 成像原理
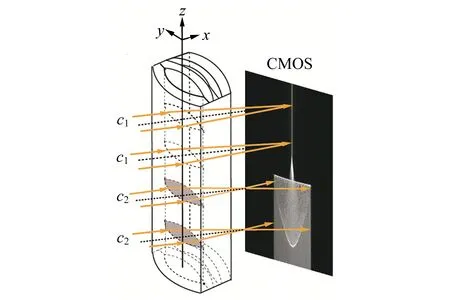
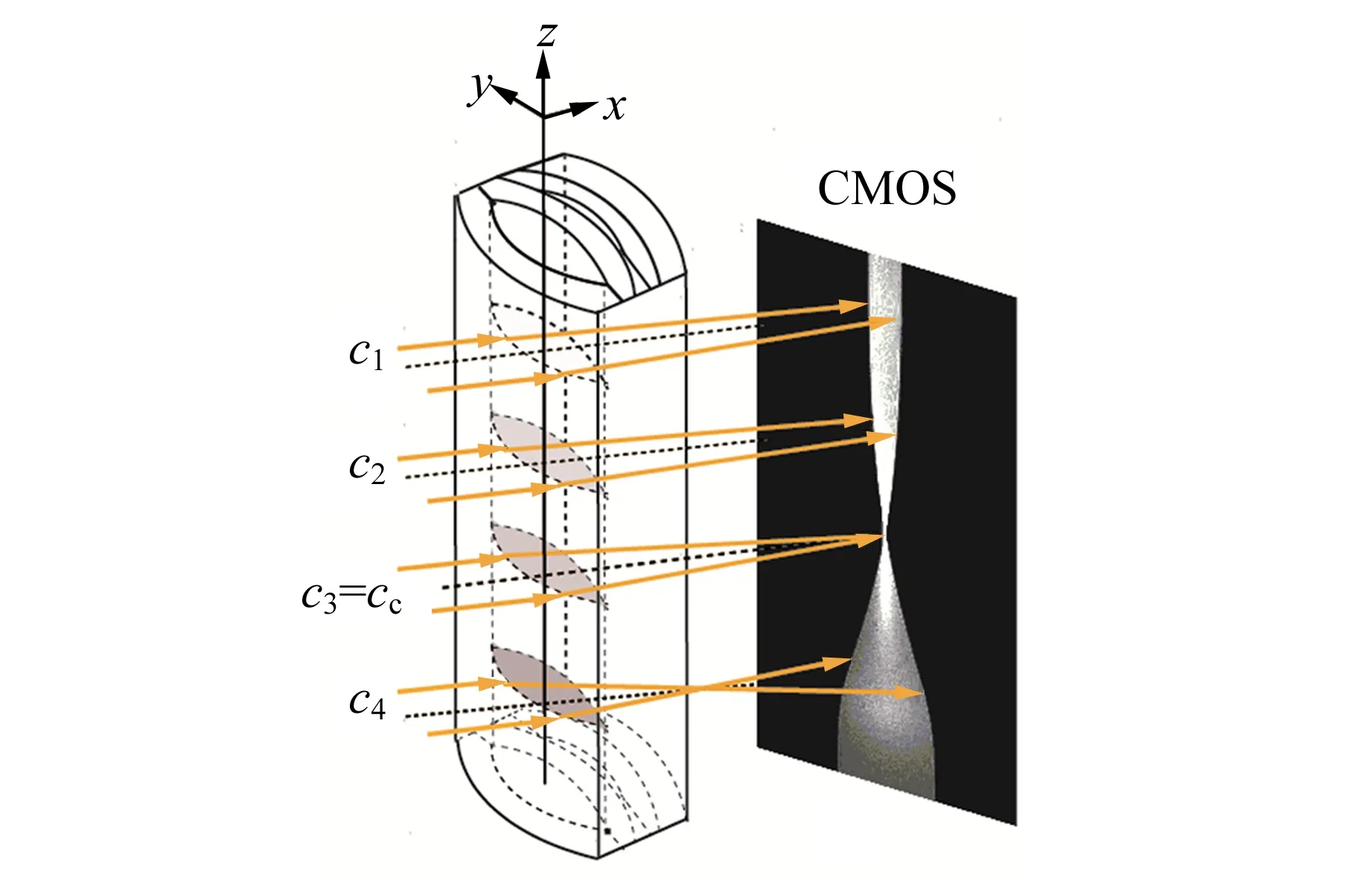
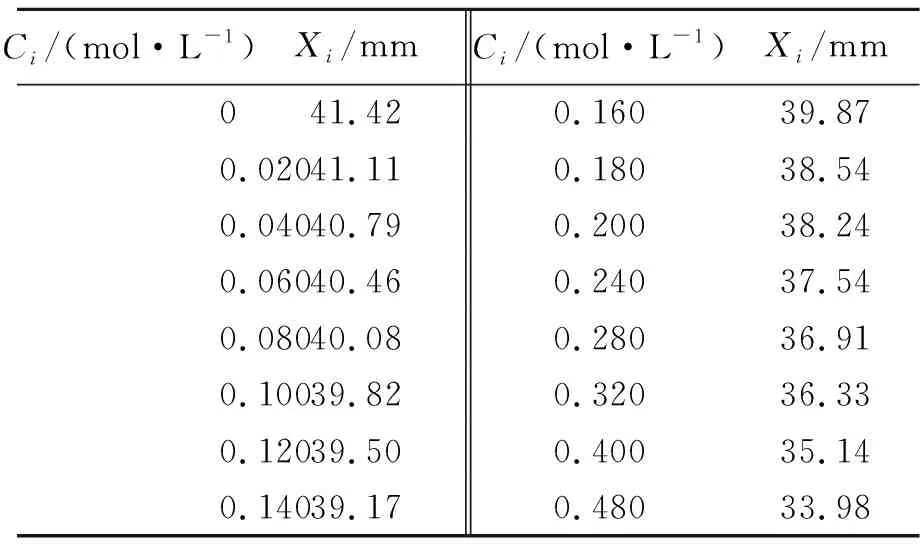
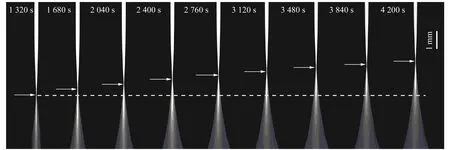
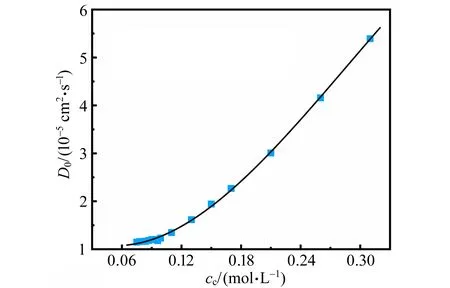
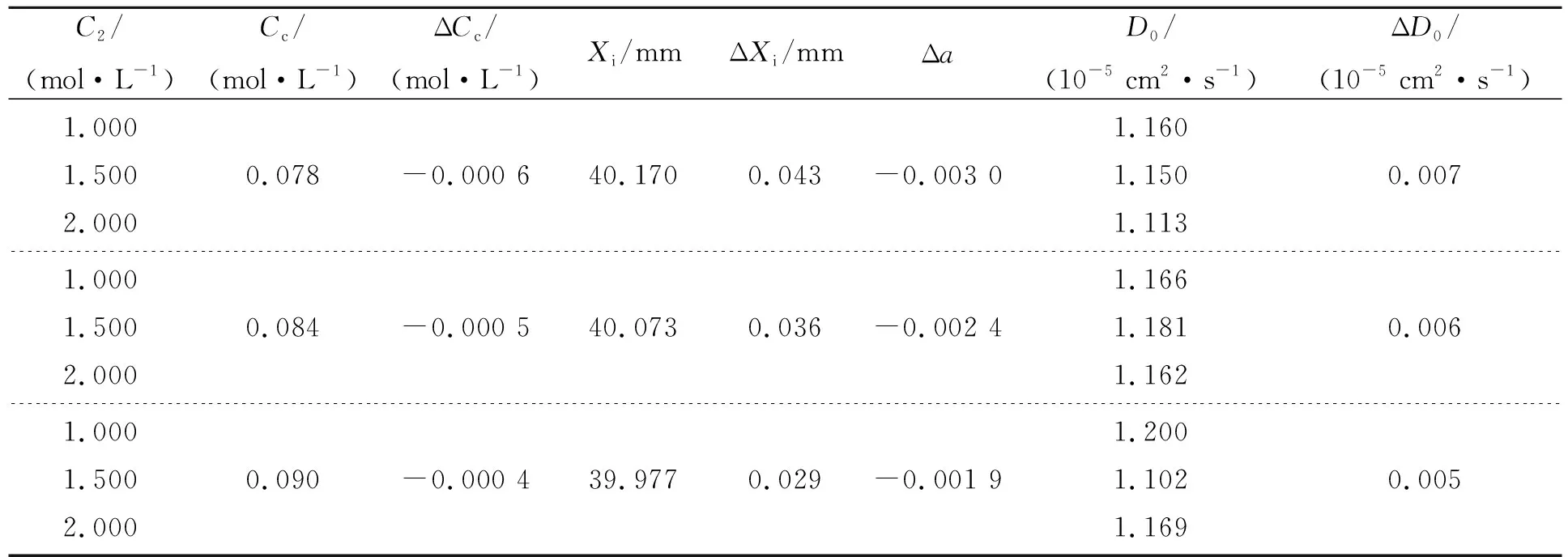
消球差液芯柱透鏡由2片對稱液芯柱透鏡和2片膠合在一起的輔助透鏡構成[12],如圖1所示. 對稱液芯柱透鏡的芯區具有擴散池作用,輔助透鏡具有消球差作用. 在液芯柱透鏡內注入濃度為C1的液體,單色準直光束經過液芯柱透鏡后,在其焦平面上會聚成1條明亮的細線,如圖1(a)所示. 在液芯柱透鏡內上、下半區分別注入濃度為C1和C2的液體(C1 (a) (b) (c)圖1 消球差液芯柱透鏡成像原理圖 由于擴散是動態過程,擴散圖像隨時間的變化能夠可視化地表現出微觀分子的擴散運動;擴散圖像束腰位置的移動速率,可用于測量擴散體系的液相擴散系數. 在非穩態擴散過程中,擴散溶液的濃度分布C(z,t)是時間的函數,該函數滿足Fick第二定律,用二階偏微分方程可以表示為 (1) 其中,D表示擴散系數,一般而言,D是濃度的函數,即D=D(C),因此式(1)可以展開為 (2) 式(1)和式(2)沒有解析解. 但對于小濃度差[?C(z,t)/?z較小,即溶液無限稀]或擴散系數的濃度變化率較小[?D(C)/?C~0]的條件下,D值可看作是與濃度無關的常量D0,因此式(2)可以簡化為 (3) 在初始條件與邊界條件下, (4) 將上式代入式(3),C(z,t)可以用誤差函數[erf(ζ)]表示為 (5) (6) 已知C1,C2和C(z,t)=Cc,式(6)中的反誤差函數有明確的數值,令其為a,則式(6)可簡寫為 (7) (8) 比較式(7)和式(8)即可求出擴散系數D0. 基于液芯柱透鏡的實驗測量裝置如圖2所示. 激光器發出的單色光束(λ=589 nm)通過準直擴束系統(由顯微物鏡、針孔濾波器[13]及球面透鏡組成)和限寬狹縫后,進入消球差液芯柱透鏡,經柱透鏡折射后,在其焦面上形成束腰狀的擴散圖像,并由圖像采集系統(CMOS相機)記錄成像. CMOS的分辨率為4 096×4 096 pixel,像元尺寸為4.5 μm×4.5 μm. 消球差液芯柱透鏡置于半導體溫控裝置內,透鏡及擴散溶液的溫度控制在室溫(25.0±0.1) ℃條件下. 圖2 實驗裝置圖 1)用型號為FA2004的電子天平(上海舜宇恒平科學儀器有限公司)稱量葡萄糖樣品,用EU-LS-100TJ型超純水器(南京歐鎧環境科技有限公司)產出的去離子蒸餾水配置不同物質量濃度的葡萄糖水溶液. 將濃度為Ci(i=1,2,…,n)的葡萄糖水溶液依次注入液芯柱透鏡的液芯區,當單色準直光束通過柱透鏡后,移動CMOS相機分別測量出其準確成像的位置Xi(i=1,2,…,n). 采用多項式擬合法確定成像位置Xi與濃度Ci之間的函數關系X(C). 2)用數字注射泵在柱透鏡芯區下方注入初始擴散濃度為C2的葡萄糖水溶液,注入時保證溶液沒有沾在透鏡上半部分的內壁上,注入后靜置10 min以消除注入溶液的湍流. 用注射泵以0.25 mL/min的速度沿透鏡內壁緩慢地將相同體積的去離子蒸餾水(C1=0)注入到透鏡上方,定義2種溶液剛接觸的時刻為擴散過程的初始時刻(t0=0). 3)根據實驗需要,選擇擴散溶液中的等濃度薄層,由擬合的X(C)函數關系可計算出單色準直光束通過此薄層后在CMOS芯片上清晰成像的位置Xc,利用位移平臺將CMOS相機移動并固定在Xc位置上. 為減小注液時的湍流對擴散造成的影響,及保證半導體溫控裝置的穩定性,擴散開始20 min后,需每隔120 s采集記錄1幅擴散圖像. 配置了16組葡萄糖水溶液,其物質量濃度為Ci,將不同濃度的葡萄糖水溶液分別注入液芯柱透鏡芯內,測得準直光束在CMOS芯片上的準確成像位置Xi,如表1所示. 分別用1次、2次和3次曲線擬合法確定成像位置Xi與濃度Ci之間的函數關系. 經過對比發現,3次曲線擬合的相關系數最高,R2=0.999 9,故本文通過3次曲線擬合結果確定X(C),如式(9)所示,其反函數如式(10)所示. X=5.8C3-1.9C2-15.92C+41.42, (9) C=-0.000 1X3+0.013X2-0.57X+9.3. (10) 在液芯柱透鏡的下方注入初始濃度為C2=1.000 mol/L的葡萄糖水溶液,上方注入C1=0 mol/L的去離子蒸餾水,選擇能夠清晰成像濃度為Cc=0.084 mol/L的等濃度薄層. 根據式(6)可計算出a=0.975. 表1 不同濃度葡萄糖水溶液的成像位置 表2對應的擴散圖像隨時間的變化規律如圖3所示,圖像束腰位置(圖中箭頭所指位置)隨時間的演變過程,能夠可視化地表現出微觀分子的擴散運動. 這是本實驗可以形象化地觀察擴散過程的獨特優勢. 表2 葡萄糖水溶液擴散過程中束腰位置隨時間的變化 圖3 CMOS采集到的不同時刻的擴散圖像 等濃度薄層的選擇和液芯柱透鏡的焦深是影響擴散系數測量的2個主要因素,下面對其進行分別討論. 為確定合適的等濃度薄層Cc值,在初始擴散濃度取固定值C2=1.000 mol/L的條件下,選擇不同等濃度薄層,重復2.2節描述的實驗步驟,擴散系數D0的測量值隨Cc值的變化如圖4所示. 圖4表明,D0隨Cc值的增加而變大,但在Cc小于0.1C2后,D0趨于穩定. 圖4的曲線變化規律反映了式(3)的成立條件,即小濃度差近似條件. 在Cc≤0.1C2后,小濃度差近似條件得以滿足才可以運用文中的式(3)~(7),所以,Cc≤0.1C2可以作為本實驗Cc值的選擇條件. 初始擴散濃度C2也可能是影響測量結果的因素. 為確定C2對測量結果的影響,在等濃度薄層滿足Cc≤0.1C2的條件下,選擇初始濃度不同的(C2=1.000, 1.500, 2.000 mol/L)葡萄糖水溶液重復2.2節描述的實驗步驟,測量結果如表3所示. 結果表明,選擇不同的C2值,測得D0值基本穩定,可見測量結果與葡萄糖水溶液的初始濃度無關. 圖4 擴散系數D0的測量值隨Cc的變化 此外,當確定C2值,分別選取3個不同的Cc值時,D0的測量結果也基本穩定,進一步驗證了Cc≤0.1C2可以作為Cc值的選擇條件. 表3中9組擴散系數的平均測量結果為D0=(1.156±0.029)×10-5cm2·s-1,與文獻[14]中的測量值接近. 在成像系統的焦平面附近,探測器非失真成像所允許調節的間距就是系統的焦深[15]. 焦深是影響擴散系數測量的另一因素. 對比式(7)和式(8),擴散系數可以表示為 (11) 式中,k是式(8)擬合得到的斜率值,在相關系數R2=0.998 1的條件下,液相擴散系數的測量誤差(ΔD0)主要由a的偏差值(Δa)導致,進而由等濃度薄層的濃度偏差值(ΔCc)確定. 根據式(10),等濃度薄層焦點位置(Xi)的不確定量(ΔXi,焦深值)決定了濃度偏差值ΔCc,即: (11) 表3 初始擴散濃度(C2)與等濃度薄層(Cc)對測量結果的影響 根據以上分析,對不同等濃度薄層(Cc)的焦點位置(Xi),測量了對應的焦深值(ΔXi);根據焦深值ΔXi,分別計算了偏差值ΔC,Δa和ΔD0,計算結果如表3所示. 通過計算,可以得出焦深造成的擴散系數偏差值在10-8cm2·s-1量級. 本文基于消球差液芯柱透鏡搭建了光學檢測系統,采用等濃度薄層移動測量法,在室溫下測量了葡萄糖水溶液的液相擴散系數,測量結果為D0=(1.156±0.029)×10-5cm2·s-1,與文獻測量值接近. 此外,本文還研究了不同濃度的等濃度薄層對擴散系數的影響,結果表明:當所選等濃度薄層滿足Cc≤0.1C2時,則小濃度差近似條件成立,擴散系數測量值趨于穩定;在研究初始擴散濃度對擴散系數的影響時,發現擴散系數測量值與初始濃度無關;在研究液芯柱透鏡的焦深對擴散系數測量的影響時,得到焦深造成的擴散系數偏差值在10-8cm2·s-1量級. 等濃度薄層移動測量法具有實驗裝置和操作簡單、測量結果可靠、擴散過程可視化等特點,為物理、化工、生物、醫療等領域對擴散系數的測量提供了新的有效手段.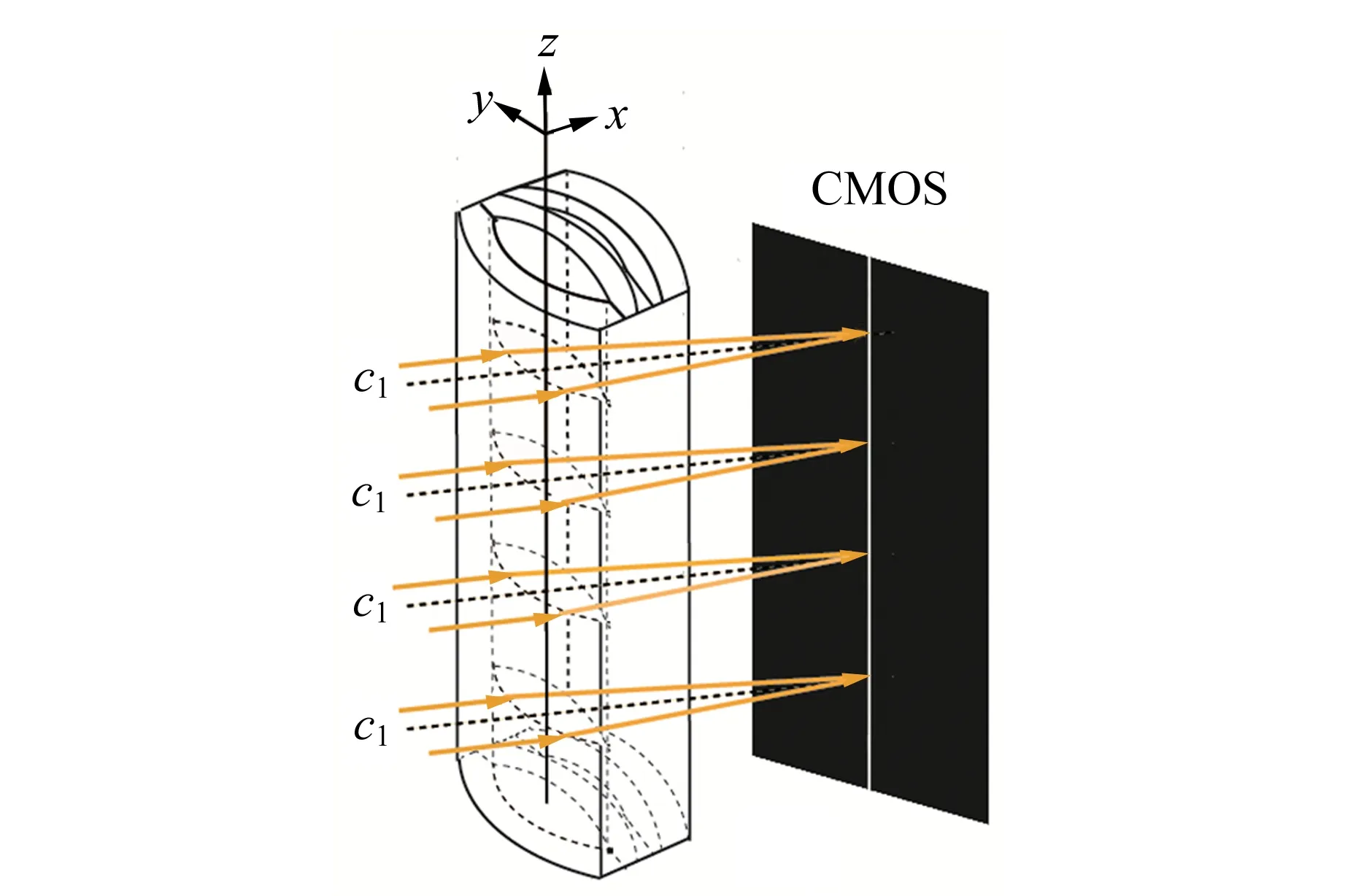
1.2 計算理論
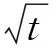
2 實驗內容
2.1 實驗裝置
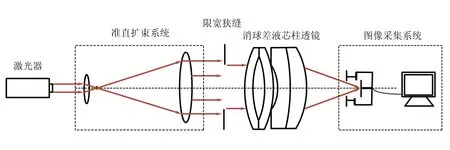
2.2 實驗步驟
3 實驗結果及分析
3.1 X(C)及C(X)函數關系的確定
3.2 實驗結果
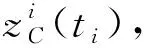
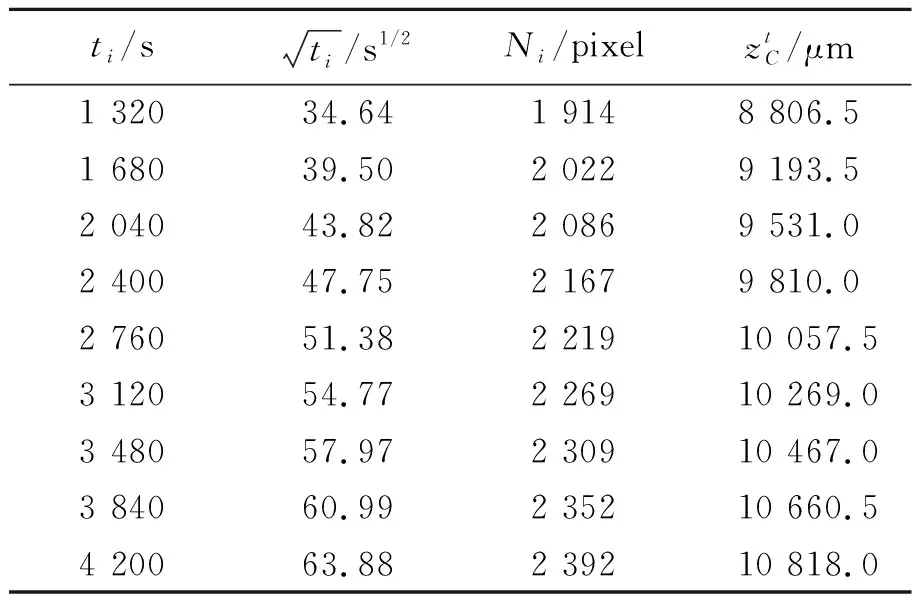
3.3 實驗結果影響因素分析
4 結 論

