轉臺齒輪傳動系統的誤差建模及其精度分配研究*

熊奉奎,張 明,袁越錦,付軍豪,劉 康

(1.陜西科技大學 機電工程學院,陜西 西安 710016;2.綿陽職業技術學院,四川 綿陽 621000;3.四川輕化工大學,四川 自貢 643000)

0 引 言

齒輪傳動是現代機械工業中核心的傳動機構,因此,對齒輪傳動系統進行傳動誤差建模計算及精度分配,無疑也就成為了對現代機械進行優化設計的關鍵[1]。

在齒輪傳動系統傳動誤差建模計算上,大連理工大學的張凱[2]提出了針對直齒圓柱齒輪傳動系統的彈性誤差運動模型,揭示了直齒齒輪傳動系統誤差與各零件的幾何誤差、彈性變形之間的內在聯系;但其未對斜齒齒輪進行探究。王保民等人[3]綜合考慮了影響齒輪副傳動誤差的轉角偏差與裝配偏心誤差,建立了切向綜合公差與輸出齒輪的最大角度誤差的關系式,及法向側隙與空間回轉角的關系式。王朝兵等人[4]針對行星齒輪系,將各齒輪的齒距偏差及偏心誤差等隨機誤差映射到哨合線上,建立了多級傳動誤差剛性親合模型,并結合蒙特卡洛法,剝離出了對傳動誤差影響最大的隨機誤差;但其未對傳動誤差進行系統的數學建模計算。

在齒輪傳動系統精度分配上,傳統精度分配均建立在確定的精度分配原則和方法上,例如相似原則、等公差原則、等影響原則、成比例影響原則、等精度原則等[5]。然而，在實際生產中,上述方法普遍存在沒有與齒輪的具體結構特征相結合的問題,例如:齒輪的尺寸大小、齒距累計誤差、齒輪軸向跳動誤差等特征。故采用上述傳統精度分配方法對齒輪傳動系統進行精度分配,在實際生產時還需人為進行調整、搭配,反復核算和試驗,不具備良好的自適應性及魯棒性[6]。

本文以新型航發葉片加工五軸機床轉臺[7]26為例,先建立從單個齒輪到一對齒輪，再到齒輪傳動系統的分步誤差計算方法;進而建立以概率統計法為基礎的傳動誤差數學模型,對傳動誤差進行計算;然后再建立基于多目標優化遺傳算法的傳動精度分配方案,對傳動系統的齒輪精度進行分配;最后將兩者結合使用,得到一個傳動系統優化設計方案,并通過實驗對優化設計方案進行驗證。

1 轉臺齒輪傳動系統傳動誤差分析

1.1 新型轉臺結構簡介

新型轉臺傳動系統結構形式如圖1所示。

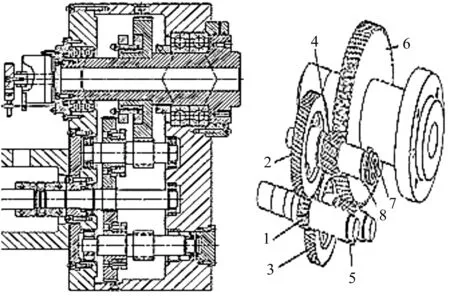
圖1 轉臺傳動結構1—主動齒輪軸;2,3—斜齒輪;4,5—中間齒輪軸;6—輸出軸斜齒輪;7—推力球軸承;8—開槽碟簧

齒輪傳動系統工作原理為:

在裝配時扭轉調節從動斜齒輪2與斜齒輪軸4的相對角度位置,同時以相同的方法調節從動斜齒輪3與斜齒輪軸5的相對角度位置,以保證主動斜齒輪軸1同一個齒的正反兩面分別和從動斜齒輪2和3的對應齒的反正兩面緊密嚙合,而斜齒輪2和3的嚙合齒的另外兩個齒面則和斜齒輪軸1的齒面留有較大間隙,而不能形成有效嚙合;

同時,輸出軸上的斜齒輪6和斜齒輪軸4和5也以同樣的原理相嚙合,最終保證輸入斜齒輪軸1進行正反轉切換時,分別從相異的傳動鏈傳遞運動和扭矩;而另一條非工作傳動鏈總是做隨動運動,且不產生運動干涉,從而達到消除正反轉切換誤差的目的[7]27。

1.2 單個齒輪傳動誤差的影響因素分解

傳動誤差是指在齒輪傳動系統中,瞬時速比對理想速比的偏差,其最終導致讀數齒輪的實際轉角偏離理論轉角[8]。因此,新型轉臺的傳動誤差可以認為是,輸出齒輪6的實際轉角位置相對理想轉角位置的偏差。大量研究表明,傳動誤差由固有位置誤差、裝置誤差及工作過程中的形變誤差3部分組成[9]。

1.2.1 齒輪固有位置誤差

齒輪固有位置誤差來自齒與齒的位置誤差和齒輪旋轉位置誤差的綜合作用[10],主要源于齒輪的加工過程。

齒與齒的位置誤差是實際齒廓對理想齒廓的偏離,影響齒與齒的位置誤差的主要因素是基節誤差和齒形誤差,也可以叫做齒輪的大周期誤差。

齒輪旋轉位置誤差主要是由于幾何偏心(齒輪實際旋轉中心對理論旋轉中心的軸線偏離距離)和運動偏心(齒廓相對理論位置產生切向位移和歪斜)造成的正弦位置誤差,其總是在齒輪轉動時隨轉角θ做正弦變化,也可以叫做齒輪的小周期誤差[11]421。

綜上所述,齒輪的固有位置誤差主要由基節誤差、齒形誤差、幾何偏心、運動偏心4個誤差因素組成。這些誤差因素綜合后造成齒輪的回轉中心產生偏移,形成齒輪的綜合偏心誤差e[11]421。

齒輪的綜合偏心誤差e對齒輪傳動誤差的影響如圖2所示。

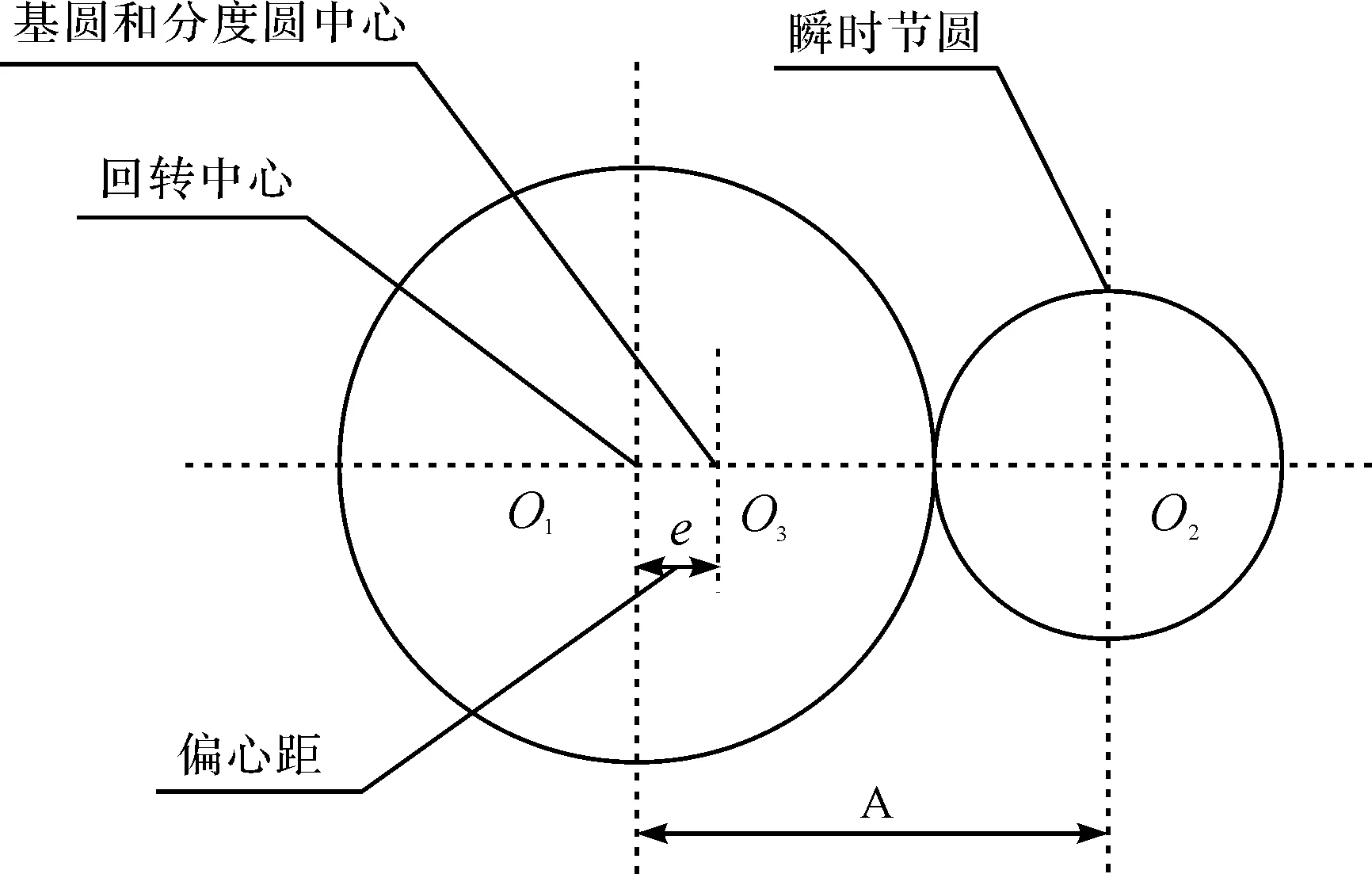
圖2 綜合偏心誤差對傳動誤差的影響

由圖2可得,假設主動齒輪1沿逆時針方向轉動,則從動齒輪2沿順時針方向轉動,當齒輪1的回轉中心產生一個e的偏心量時,齒輪固有位置誤差為[12]:

(1)

式中:Δ1—齒輪固有位置誤差;e1—主動齒輪的偏心距;φ1—齒輪的偏心距與回轉中心之間o1o2的夾角;αn—斜齒輪的壓力角;esinφ1—偏心距產生的傳動誤差;ecosφ1tanαn—從動齒輪產生的傳動誤差。

齒輪的固有位置誤差為:

(2)

由式(2)可知,齒輪的偏心距e引起的齒輪傳動誤差Δ1符合三角正弦函數變化規律。

(3)

1.2.2 裝置誤差

在轉臺實際運轉的過程中,齒輪2的轉動中心位置無疑非常重要[13]。裝置誤差是齒輪2實際轉動中心對理論轉動中心的偏離,相當于齒輪2發生了幾何偏心。裝置誤差由齒輪孔與軸頸間的間隙Δe2、齒輪安裝處軸頸的徑向跳動Δe3和軸承的徑向跳動Δe4組成[7]28。

3個誤差對齒輪傳動誤差的影響的分析方法與齒輪偏心造成的傳動誤差分析方法一致,其計算公式為:

(1)齒輪孔與軸間的間隙偏心e2導致的傳動誤差Δ2:

(4)

(2)軸頸的徑向跳動偏心e3導致的傳動誤差Δ3:

(5)

(3)軸承的徑向跳動偏心e4導致的傳動誤差Δ4:

(6)

(4)齒輪孔與軸之間的間隙Δe2與偏心e2的關系為:

(7)

(5)軸頸的徑向跳動Δe3與偏心e3的關系為:

(8)

(6)軸承的徑向跳動Δe4與偏心e4的關系為:

(9)

式中:Δei—齒輪的各跳動量,均服從正態分布;φi—齒輪的各跳動量對應的相位角,均在區間[0,2π]上服從均勻分布。

1.2.3 工作過程中的形變誤差

在轉臺傳動系統工作過程中,齒輪會受到間歇性隨機載荷作用,從而產生變形,最終映射到齒輪的傳動誤差上(即變形誤差)。變形誤差主要是來源于磨損誤差、塑性變形誤差、彈性變形誤差、熱誤差及疲勞變形誤差。而塑性變形和疲勞破壞,均屬于齒輪典型的失效形式之一,不在誤差的研究范圍之內。

而對于斜齒輪變形(磨損)的誤差補償,此處筆者采用了非標碟簧開槽隨動補償機構予以補償,并在筆者已發表的論文《新型轉臺開槽碟簧隨動補償磨損誤差機構設計》中有詳細分析。

1.3 轉臺齒輪傳動系統傳動誤差分析

1.3.1 單個齒輪傳動誤差

由誤差獨立作用原理可得,單個齒輪的誤差是由齒輪的固有位置誤差和裝置誤差組合得到的。由參考文獻[7]得,單個齒輪的傳動誤差ΔE的計算公式為:

ΔE=Δ1+Δ2+Δ3+Δ4

(10)

1.3.2 一對齒輪副的傳動誤差

一對齒輪副的傳動誤差則是由兩個互相嚙合的齒輪的傳動誤差組合而成,由讀數法可得其計算公式為:

(11)

式中:Δθf—齒輪副的傳動誤差;ΔE1，ΔE2—分別為主動齒輪和從動齒輪的傳動誤差;R2—從動齒輪的分度圓半徑。

1.3.3 齒輪傳動系統的傳動誤差

將齒輪傳動系統中所有齒輪副的傳動誤差合理地累加到讀數齒輪上,就能得到齒輪傳動系統的整體傳動誤差。如果取第n軸為讀數齒輪軸,則齒輪傳動系統的整體傳動誤差的計算公式為[7]29:

(12)

式中:Δθfn—第n對齒輪副的傳動誤差;in—第n對齒輪副上n軸到n+1軸的傳動比。

對于新型轉臺而言,參考式(12),并以齒輪6為讀數齒輪,轉臺傳動系統的傳動誤差為:

(13)

式中:Δθf1—齒輪1與2的嚙合傳動誤差;Δθf2—齒輪4與6的嚙合傳動誤差;i2—齒輪4與6的傳動比。

2 轉臺傳動系統傳動誤差建模計算

由1.2節可推得,組成傳動誤差的各個誤差因素均為隨機變量,因此傳動誤差也一定為隨機變量,最后計算齒輪傳動誤差時,就難免需要考慮各誤差因素的均值μ和方差D。以概率統計法為基礎,筆者采用數學建模的方法,對傳動誤差進行計算。

(14)

(15)

其中,齒輪孔與軸之間的間隙偏心e2服從瑞利分布,相位角服從在[0,2π]區間的均勻分布。

由概率論可知:

(16)

(17)

又因為Δe2服從正態分布,所以標準差為:

(18)

由于隨機變量e2和φ2是互相獨立的,有:

(19)

又因為:E[sin(φ2+αn)]=0,所以有:

μ2=0

(20)

裝置誤差中,各間隙Δei均服從正態分布,所以齒輪安裝處軸頸的徑向跳動偏心e3和軸承的徑向跳動偏心e4所引起的傳動誤差Δ3,Δ4的均值和方差分別為[14]2912:

μ3=0

(21)

μ4=0

(22)

一對齒輪的傳動誤差的均值和標準差為:

μ1,2=0

(23)

齒輪傳動系統的傳動誤差也服從正態分布,若分布范圍取6σ1,2,則傳動誤差的極值為:

(24)

相應角傳動誤差Δφ1,2的均值和標準差分別為:

μφ1,2=0

(25)

式中:mn—法向模數;z2—從動輪齒數。

綜合式(14～25)得,一對齒輪的角傳動誤差為:

(26)

式中:F′i1,F′i2—主動輪和從動輪的切向綜合誤差;Δe21,Δe22—主動輪和從動輪的孔與軸間的間隙;Δe31,Δe32—主動輪和從動輪的安裝處軸頸徑向跳動誤差;Δe41,Δe42—主動輪和從動輪的軸承徑向游隙。

根據式(25,26),并結合讀數法,可得轉臺傳動系統的傳動誤差計算模型為:

(27)

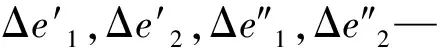
3 轉臺齒輪傳動系統的精度分配

3.1 遺傳算法簡介

遺傳算法是一類隨機優化搜索方法,該算法直接對結構對象進行操作,不存在求導及函數連續性的限定,具有更好的內在并行性和全局搜索能力;采用概率化的尋優方法,能自動獲取優化的搜索空間,自適應地調整搜索方向,不需要確定的規則。該算法一般由:編碼、初始群體的生成、雜交、適應度值評估檢測、選擇、變異和中止7個步驟構成[15]126。

3.2 精度分配優化數學建模

3.2.1 設計變量

轉臺傳動系統的單側傳動鏈有4個齒輪,根據1.2節的分析,筆者選取齒輪的切向綜合誤差、齒輪孔與軸頸之間的間隙、安裝處軸頸徑向跳動誤差和軸承徑向游隙為系統傳動誤差設計變量。

由于齒輪1和齒輪4是齒輪軸,其齒輪孔與軸頸之間的間隙及安裝處軸頸徑向跳動誤差的值均為0,轉臺傳動系統的精度分配模型由12個設計變量構成,如表1所示。

表1 精度分配設計變量

3.2.2 約束條件

約束條件直接決定優化結果的準確性。筆者先根據新型轉臺傳動系統中,各齒輪不同精度等級(取5級到8級)選取變量的取值范圍,再依據齒輪不同的精度等級查閱機械設計手冊,確定每個齒輪的x1、x2、x3及x4的取值范圍,如表2所示。

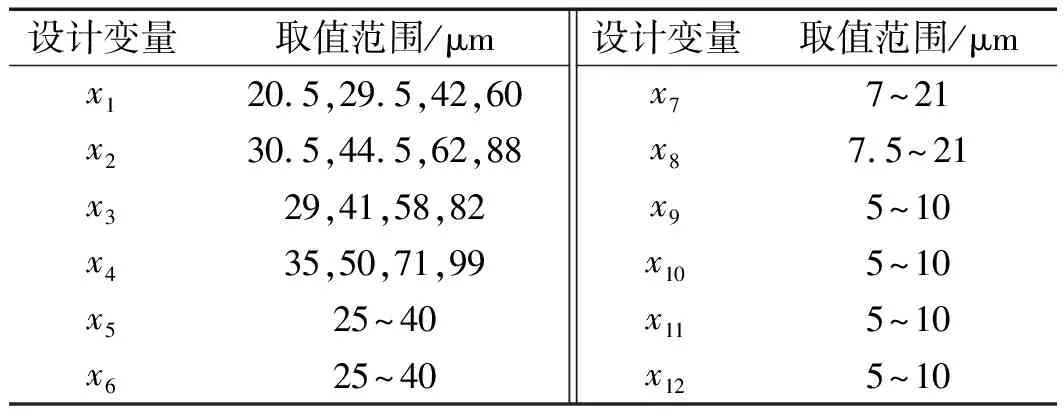
表2 設計變量的取值范圍

轉臺設計的定位精度要求低于8″。由于轉臺由SINUMERIK-840D全閉環控制系統控制,其定位精度要比開環系統高一個數量級,故滿足小于等于80″即可。

基于機床工作時熱誤差的影響,筆者將誤差允許值設定為61″;結合式(13)可得其優化目標應滿足誤差的約束條件為:

(28)

3.2.3 目標函數確定

目標函數會影響優化模型的性能，由單一目標函數得到的優化解常具有局限性[16]。因此,本文采取多目標優化的方法,設定成本、均衡及魯棒3個目標函數為優化目標,并用適應度函數對其進行尋優求解,進而得到一個新的適應度函數,最后用遺傳算法求解尋優后的新適應度函數,得到合理的精度分配方案。

(1)成本目標函數

降低生產成本是新型轉臺精度分配的重要目標之一。在多指標評價體系中,由于各評價指標性質不同,通常具有不同的量綱和數量級[17],需對設計變量進行歸一化處理,即:

(29)

因此,成本目標函數的公式為:

(30)

(2)均衡目標函數

在精度分配中,應避免出現一個誤差值很低,一個誤差值很高。另外,由于齒輪誤差值具有離散性,應對相應齒輪的軸向跳動誤差和徑向跳動誤差進行均衡化處理[15]125,其均衡目標函數為:

(31)

(3)魯棒目標函數

為盡量增加轉臺齒輪傳動系統誤差的穩定性,可以采取降低設計變量誤差值的措施。基于敏感度分析設計魯棒目標函數為:

(32)

(4)適應度函數轉化

適應度函數是按照最小值進行且有約束的,針對線性方程的最優值尋優的函數[14]2913,筆者將以上3個目標函數用適度性函數進行轉換,可得:

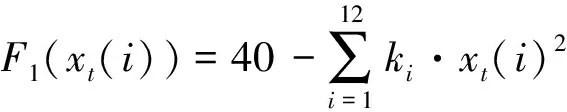
(33)

采用權重法,并結合轉臺結構,筆者確定成本、均衡及魯棒目標函數加權系數分別為c1=0.5,c2=0.3,c3=0.2,則簡化后新的適應度函數為:

(34)

由于設計要求是,完成精度分配后的轉臺傳動誤差的最大求解值要小于轉臺傳動誤差設計允許值。但是適應度函數默認求解的是轉臺傳動誤差的最小值,需要對適應度函數添加負號,經轉換求得精度分配后的傳動誤差的最大值。用遺傳算法所求的函數為:

(35)

滿足的約束為:

(36)

3.3 精度分配計算

根據上述理論,筆者使用MATLAB編寫多目標優化后的遺傳算法程序[18],并取交叉概率0.7,變異概率0.3,進化次數500,種群規模500;運行后得到轉臺的齒輪優化數據。

前5級精度齒輪參數如表3所示:

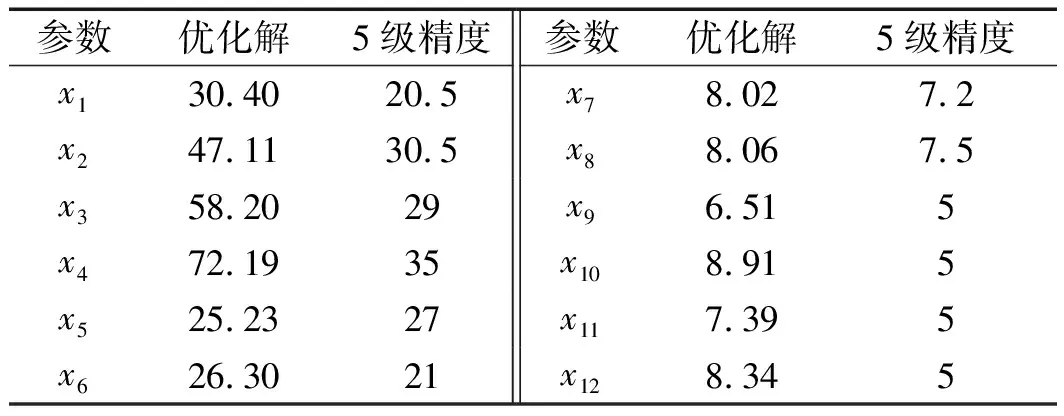
表3 高精度分配方案

從優化結果可以看出:齒輪1、2、4和6的切向綜合誤差的選取可以適當增大,孔與軸之間的間隙變化不大,安裝處軸頸徑向跳動誤差可以適當提高,軸承徑向游隙無明顯變化。

根據齒輪的切向綜合誤差的變化值,筆者對轉臺傳動系統的齒輪進行重新選取。優化后的齒輪精度等級變化如表4所示。

表4 優化前后齒輪精度等級對比

式(27)中,代入精度優化分配前5級精度齒輪參數,經計算可得:傳動誤差概率統計集中值為18.4″。

同理,代入優化后的設計參數,可得精度優化后的傳動誤差最大值為54.7″<61″,概率統計集中值為27.61″,小于轉臺齒輪傳動系統設計的允許設計傳動誤差范圍,滿足設計要求,可見其精度分配合理。

從優化后的齒輪精度等級表格中可以看出,在滿足設計誤差要求的前提下,各齒輪的精度等級均有所下降,達到了優化設計目標,降低了制造成本。

4 傳動誤差模型試驗驗證

為了驗證該傳動誤差計算模型及齒輪精度分配方案的正確性,筆者以6級精度斜齒輪組的減速機作為載體,搭建實驗平臺(新型轉臺已投產,實物不方便拆卸),予以間接驗證。

4.1 實驗原理

筆者以齒輪減速機作為載體,在變頻器和三相電機構成的動力組合的驅動下,實現針對減速機輸入轉速的無極變速,模擬加工過程中轉臺的轉速變化,實現對現實加工環境的模擬;通過分別連接在斜齒輪輸入軸、中間軸和輸出軸上的3個角速度編碼器,實時監測各軸的實時轉速和運動狀態;再通過接線端子,將數據實時傳送到PCL—833多功能采集卡上,由采集卡采集后傳輸到工控主機采集數據;然后將數據經過角度轉化處理,得到同一時間點各軸的轉速值。

最后,筆者再通過MATLAB編程制圖,將各點的數據輸入其中,形成對應的誤差曲線,并與分析結果進行對比,驗證理論計算體系的正確性。

實驗平臺搭建原理如圖3所示。

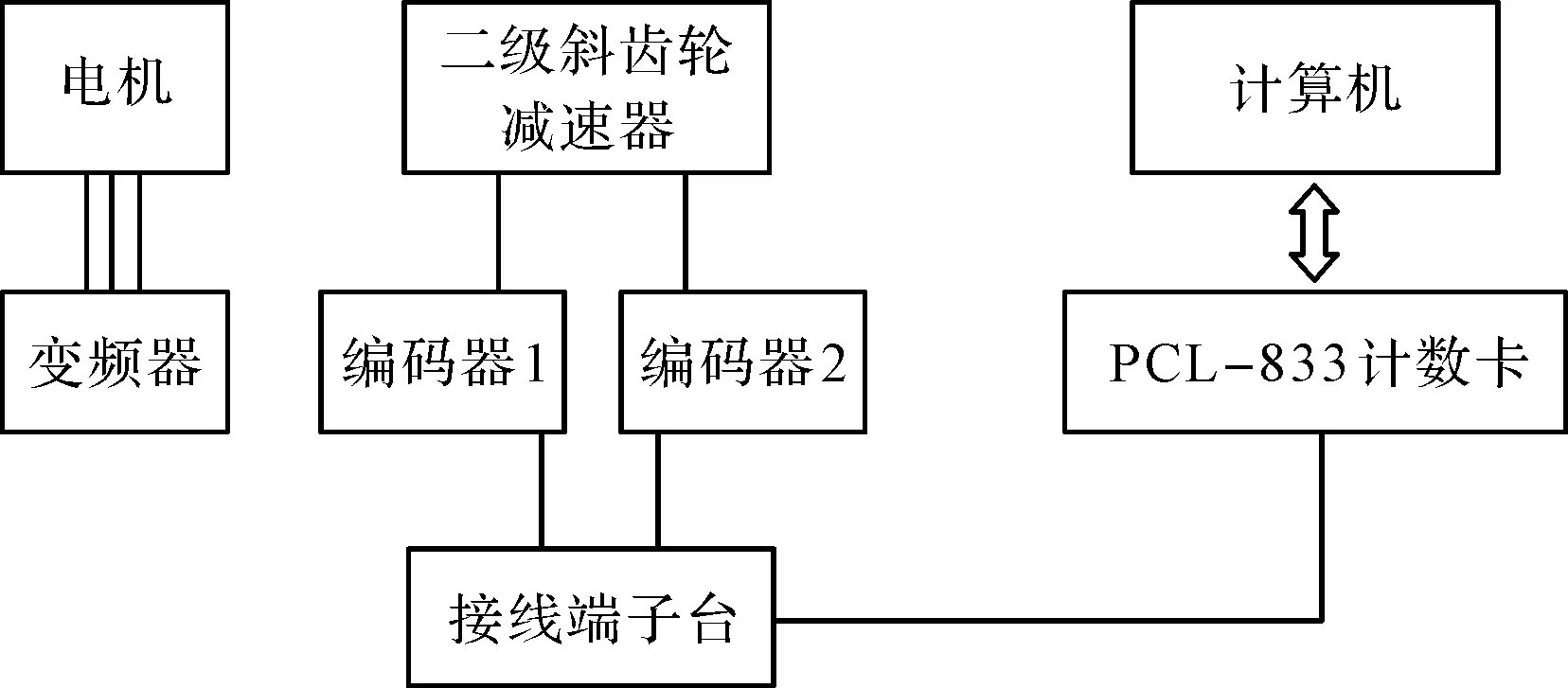
圖3 試驗平臺搭建原理圖

圖3中,實驗平臺中檢測出的斜齒輪傳動系統的傳動誤差、輸入端齒輪副的傳動誤差和輸出端齒輪副的傳動誤差均能在顯示器上,通過PCL833采集卡專用軟件界面顯示出來。

按實驗原理搭建的實驗平臺如圖4所示。

圖4 實驗平臺搭建示意圖1—工控主機;2—二級斜齒輪減速器;3—角速度編碼器;4—梅花聯軸器;5—步進電機;6—變頻器;7—PCL833采集卡

4.2 實驗數據分析

啟動伺服電機后,筆者設置電機轉速為10 r/min,運行一段時間待被測齒輪轉動平穩后,再開始采集數據,采集數據過程中通過變頻器不斷變換電機轉速(n=10 r/min～960 r/min),得到并記錄輸入與輸出軸的數據,如圖5所示。

圖5 齒輪傳動系統誤差采集數據

按PCL833使用說明所述,角度轉換公式為:

(37)

式中:Δθ—傳動系統的角度誤差,分;λ—誤差采集值。

筆者不斷地記錄不同轉速下的傳動系統誤差采集值λ,再按上式將傳動誤差采集值λ轉換成角度誤差Δθ[19];最后,用MATLAB編程作圖,即得到二級減速器的傳動誤差曲線,如圖6所示。

圖6 實驗測得的系統傳動誤差曲線

4.3 實驗結論

圖6中,齒輪傳動系統傳動誤差的絕對值最大為|Δθmax|=0.83′=49.8″,且傳動系統傳動誤差的最集中值為|Δθ集中|=0.42′=25.2″。

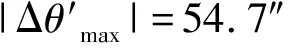
5 結束語

針對齒輪傳動系統誤差建模分析和精度分配的問題,首先,筆者在概率統計法的基礎上建立了齒輪傳動系統傳動誤差的數學計算模型;其次,在傳統遺傳算法的基礎上,對目標函數進行了多目標(成本、均衡及魯棒性)優化;同時,結合傳動系統的實際結構參數,得到了更具有工程意義的適度性函數,建立起了一套精度分配方案;最后,將精度優化分配方案融入到傳動系統傳動誤差計算數學模型中,得到了一套更具魯棒性和經濟性的齒輪傳動系統優化設計方案,并用實驗驗證了其正確性。

研究結果表明:

(1)新傳動系統優化設計方案,使傳動誤差的計算不僅能得到傳統極值法所能得到的極值,還能得到其分布規律和均值;同時提高了傳動系統優化設計的魯棒性、經濟性及工程實用性;

(2)在滿足設計要求的前提下,轉臺傳動系統使齒輪1、2及6精度等級由5級降到6級,齒輪4則由5級降到7級,降低了對單個齒輪的精度要求;同時又免去了對精度分配的人工復核和調整,使齒輪傳動系統的設計周期總體上縮短7%,最終使單個轉臺的成本下降180元,提高了新型轉臺的經濟性。

在后期的研究中,筆者準備從增加精度分配目標數的角度出發,增加目標函數的種類,以期對精度分配方案進行進一步的優化。