基于Spark的傾斜數(shù)據(jù)虛擬劃分算法
李俊麗
(晉中學(xué)院 計(jì)算機(jī)科學(xué)與技術(shù)系,山西 晉中 030619)
0 引 言
隨著大數(shù)據(jù)時(shí)代的到來(lái),數(shù)據(jù)量以驚人的速度增長(zhǎng)。大數(shù)據(jù)應(yīng)用的出現(xiàn)給數(shù)據(jù)處理帶來(lái)了巨大的挑戰(zhàn)[1,2],越來(lái)越多的高效并行計(jì)算平臺(tái),如MapReduce[3]和Spark[4-6],被廣泛采用來(lái)處理大數(shù)據(jù)。互信息是對(duì)兩個(gè)隨機(jī)變量之間共享的信息量的度量。互信息的計(jì)算量很大,特別對(duì)于處理大規(guī)模的類(lèi)別數(shù)據(jù)。互信息可以廣泛應(yīng)用于數(shù)據(jù)挖掘[7,8]算法中。為了提高互信息計(jì)算的效率,Spark內(nèi)存計(jì)算模型是最好的選擇,但要面對(duì)Spark數(shù)據(jù)傾斜的性能優(yōu)化問(wèn)題。針對(duì)Spark中的數(shù)據(jù)傾斜問(wèn)題,近年來(lái)提出了很多算法和模型。例如,文獻(xiàn)[9]提出了Spark平臺(tái)上基于特征分組的并行離群挖掘算法。SCID算法[10]設(shè)計(jì)了一種Pond-sampling算法來(lái)收集數(shù)據(jù)分布信息,并對(duì)總體數(shù)據(jù)分布進(jìn)行估計(jì)。在數(shù)據(jù)劃分過(guò)程中,SCID實(shí)現(xiàn)了Bin-packing算法對(duì)Map任務(wù)的輸出進(jìn)行桶狀處理。此外,在分區(qū)過(guò)程中,還會(huì)進(jìn)一步切割大型分區(qū)。SP-Partitioner算法[11]將到達(dá)的批次數(shù)據(jù)作為候選樣本,在系統(tǒng)抽樣的基礎(chǔ)上選擇樣本,預(yù)測(cè)中間數(shù)據(jù)的特征。該方法根據(jù)預(yù)測(cè)結(jié)果生成參考表,指導(dǎo)下一批數(shù)據(jù)的均勻分布。文獻(xiàn)[12]優(yōu)化了笛卡爾(笛卡兒積)算子。由于計(jì)算笛卡爾積需要連接操作,因此可能會(huì)出現(xiàn)數(shù)據(jù)傾斜。文獻(xiàn)[13]提出了SASM(Spark adaptive skew mitigation),通過(guò)將大分區(qū)遷移到其它節(jié)點(diǎn),同時(shí)平衡各任務(wù)之間的大小,來(lái)緩解數(shù)據(jù)傾斜問(wèn)題。與這些現(xiàn)有的方法不同,DVP算法針對(duì)文獻(xiàn)[9]中并行互信息計(jì)算中出現(xiàn)的數(shù)據(jù)傾斜問(wèn)題進(jìn)行研究和改進(jìn)。DVP算法探索了數(shù)據(jù)虛擬劃分,其中虛擬前綴附加在一個(gè)大分區(qū)中的所有鍵之前,然后是一個(gè)輔助散列。DVP中的虛擬分區(qū)確保消除了大分區(qū)。DVP算法是在Spark計(jì)算平臺(tái)上設(shè)計(jì)并實(shí)現(xiàn)的一種數(shù)據(jù)虛擬劃分的方案,主要針對(duì)數(shù)據(jù)傾斜情況下大規(guī)模類(lèi)別數(shù)據(jù)的互信息并行計(jì)算,解決了數(shù)據(jù)分布不均勻?qū)е碌臄?shù)據(jù)傾斜問(wèn)題。
1 互信息計(jì)算
互信息是信息論中對(duì)兩個(gè)隨機(jī)變量關(guān)聯(lián)程度的統(tǒng)計(jì)描述,可以表示為這兩個(gè)隨機(jī)變量概率的函數(shù)。
假設(shè)DS是一個(gè)包含n個(gè)對(duì)象的數(shù)據(jù)集,每個(gè)對(duì)象都由m個(gè)特征表示。我們使用H(yi,yj)和MI(yi;yj)分別表示集合DS上計(jì)算的特征yi和yj之間的熵和互信息。熵可以表示如下
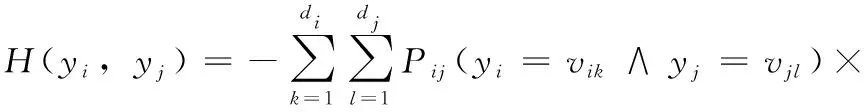
(1)
其中,Pij(yi=vik∧yj=vjl)為特征yi和yj分別等于vik和vjl的概率。式(1)中di和dj為特征yi和yj的取值個(gè)數(shù);vik和vjl可以在集合D(yi)和D(yj)中找到,其中D(yi)={vi1,…,>vidi},D(yj)={vj1,…,>vjdj}。熵H(yi,>yj)是概率Pij和logPij的乘積的函數(shù)。
MI(yi;yj)作為特征yi和yj之間的互信息。我們將互信息MI(yi;yj)表示為
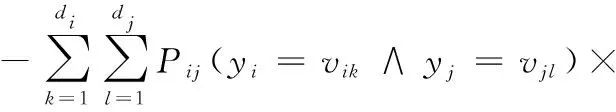
(2)
其中,概率Pij,特征yi和yj,值vik和vjl,域di和dj,集合D(yi)和D(yj)與式(1)中的相同,Pi和Pj分別為特征yi和yj等于vik和vjl的概率。
互信息可以廣泛應(yīng)用于數(shù)據(jù)挖掘算法中,DVP算法中的互信息是作為度量指標(biāo)來(lái)量化類(lèi)別數(shù)據(jù)特征之間的相似性。
2 數(shù)據(jù)傾斜
2.1 概 述
在Spark Shuffle階段,Spark必須將相同的鍵從每個(gè)節(jié)點(diǎn)拉到節(jié)點(diǎn)上的任務(wù)中。這樣的過(guò)程可能會(huì)給單個(gè)節(jié)點(diǎn)帶來(lái)沉重的負(fù)載。此時(shí),如果某個(gè)鍵對(duì)應(yīng)的數(shù)據(jù)量特別大,就會(huì)出現(xiàn)傾斜。
圖1描述了分區(qū)2總體上比分區(qū)1和分區(qū)3大。由于輸入數(shù)據(jù)分布不均勻,使用系統(tǒng)的默認(rèn)哈希分區(qū)可能導(dǎo)致子RDD中每個(gè)分區(qū)的大小存在較大差異,從而導(dǎo)致數(shù)據(jù)傾斜。當(dāng)遇到數(shù)據(jù)傾斜問(wèn)題時(shí),整個(gè)Spark作業(yè)的執(zhí)行時(shí)間由運(yùn)行時(shí)間最長(zhǎng)的任務(wù)控制,這使得Spark作業(yè)運(yùn)行得相當(dāng)慢。在最壞的情況下,由于最慢的任務(wù)處理了過(guò)多的數(shù)據(jù),Spark作業(yè)可能耗盡內(nèi)存。
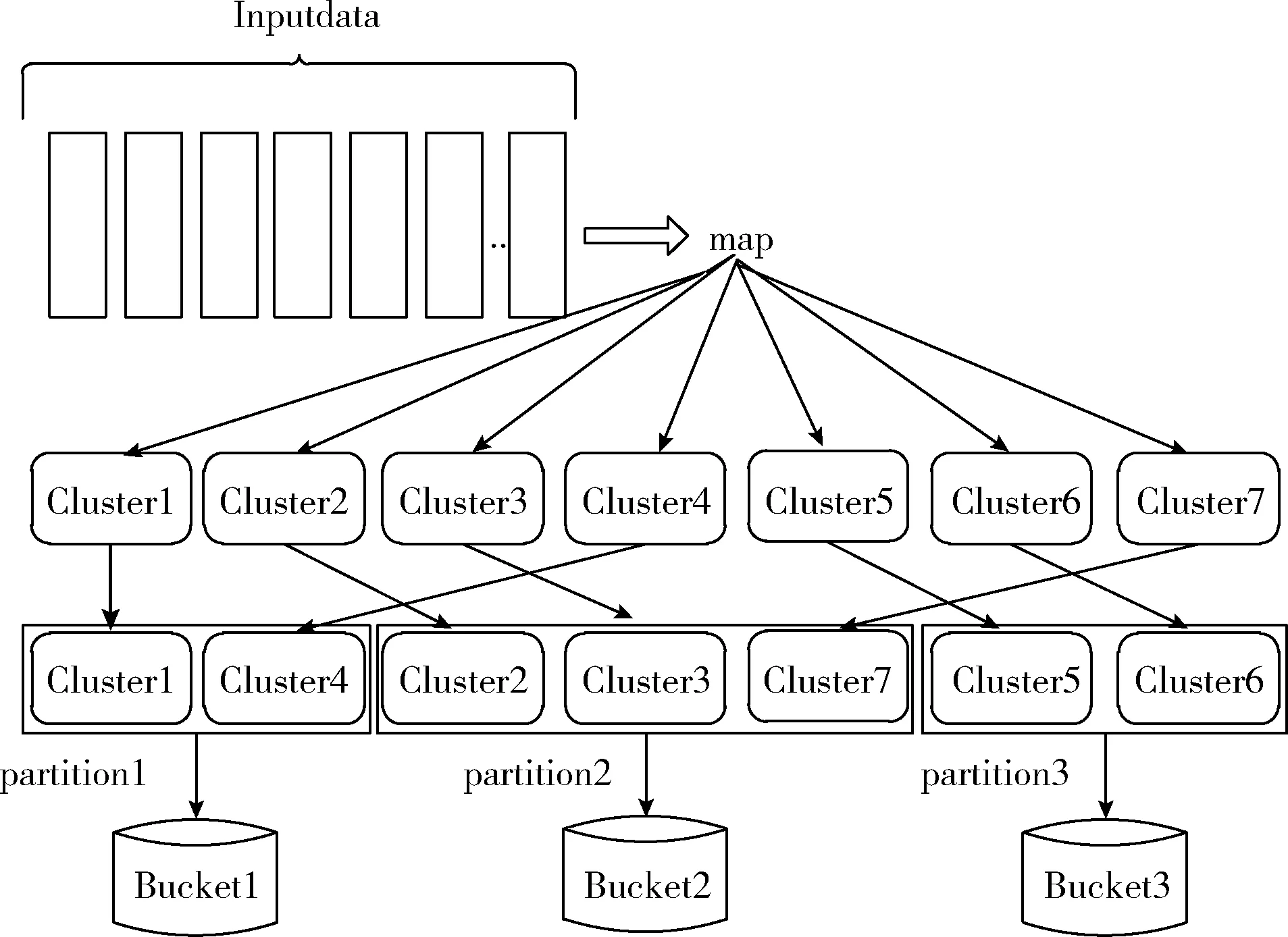
圖1 Spark Shuffle數(shù)據(jù)分布
2.2 數(shù)據(jù)傾斜模型
接下來(lái)建立了一個(gè)數(shù)據(jù)傾斜模型來(lái)量化由Spark創(chuàng)建的分區(qū)之間的數(shù)據(jù)傾斜度引起的問(wèn)題。
圖1描述了Spark集群中默認(rèn)的哈希分布機(jī)制,該機(jī)制執(zhí)行以下3個(gè)步驟。首先,Map任務(wù)檢索輸入數(shù)據(jù)。然后,這些數(shù)據(jù)由Map任務(wù)處理,Map任務(wù)生成以鍵值對(duì)格式組織的中間結(jié)果。最后,使用鍵將中間結(jié)果分組到分區(qū)中。最后一步中的一個(gè)障礙是,由于數(shù)據(jù)傾斜,這些分區(qū)的大小不均勻。
假設(shè)根據(jù)鍵值聚合數(shù)據(jù)時(shí)有p個(gè)唯一的鍵,我們?cè)O(shè)K表示鍵,K={k1,>…,>kp}。我們把V表示為集合k中所有鍵的值
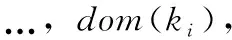
(3)
假設(shè)有p個(gè)分區(qū),每個(gè)分區(qū)中的值共享一個(gè)鍵。值得注意的是,所有分區(qū)的大小可能不同。例如,第i和第j個(gè)分區(qū)的大小分別為li和lj。這兩個(gè)分區(qū)的大小可能不同(即li≠lj)。
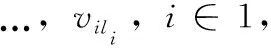
現(xiàn)在使用域dom(ki)的大小來(lái)度量鍵ki的第i個(gè)分區(qū)的大小,它的形式是|dom(ki)|。平均分區(qū)大小由|dom(K)|avg表示,|dom(K) |avg由平均域大小來(lái)衡量,具體如下表示
(4)
分區(qū)之間的數(shù)據(jù)傾斜度定義為分區(qū)大小的偏差(即,|dom(ki)|)。設(shè)(ki)為第i個(gè)分區(qū)或域dom(ki)的傾斜度。在形式上,域dom(ki)的傾斜度s(ki)如下表示
(5)
3 數(shù)據(jù)虛擬劃分方法
3.1 并行互信息計(jì)算中的數(shù)據(jù)傾斜
聚合操作符是Spark Shuffle階段的性能瓶頸。并行計(jì)算互信息的一個(gè)關(guān)鍵挑戰(zhàn)在于countByKey或reduceByKey操作符(參見(jiàn)算法1第(4)行和第(12)行),它引入了包含兩個(gè)階段的shuffle。在shuffle過(guò)程中,第一階段執(zhí)行shuffle write操作分區(qū)數(shù)據(jù)。具有相同鍵的已處理數(shù)據(jù)被寫(xiě)入相同的磁盤(pán)文件。
一旦countByKey或reduceByKey操作符執(zhí)行,第二階段中的每個(gè)任務(wù)都會(huì)執(zhí)行shuffle read操作。執(zhí)行此操作的任務(wù)提取屬于前一階段任務(wù)節(jié)點(diǎn)的鍵,然后對(duì)同一鍵執(zhí)行全局聚合或連接操作。在這個(gè)場(chǎng)景中,鍵值被累積。如果數(shù)據(jù)分布不均勻,就會(huì)發(fā)生數(shù)據(jù)傾斜。
3.2 數(shù)據(jù)虛擬劃分
數(shù)據(jù)虛擬劃分是一種針對(duì)shuffle操作(例如,reduceByKey)可能引起數(shù)據(jù)傾斜而進(jìn)行的虛擬分區(qū)機(jī)制。為了減少shuffle操作中的數(shù)據(jù)傾斜,DVP算法只在統(tǒng)計(jì)單個(gè)特征的取值時(shí)進(jìn)行虛擬分區(qū),因?yàn)樘卣鲗?duì)的取值不容易發(fā)生數(shù)據(jù)傾斜。圖2描述了虛擬分區(qū)的過(guò)程。
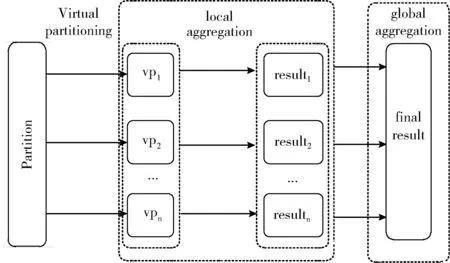
圖2 虛擬分區(qū)過(guò)程
在這里,首先為RDD中的每個(gè)鍵添加一個(gè)隨機(jī)前綴,然后是reduceByKey聚合操作。通過(guò)向同一個(gè)鍵添加隨機(jī)前綴并將其更改為幾個(gè)不同的鍵,一個(gè)任務(wù)最初處理的數(shù)據(jù)被分散到多個(gè)任務(wù)中,以便進(jìn)行本地聚合。這種虛擬分區(qū)的策略減少了單個(gè)任務(wù)處理的過(guò)量數(shù)據(jù)。刪除每個(gè)鍵的前綴后,再次執(zhí)行全局聚合操作以獲得最終結(jié)果。
3.3 DVP算法描述
DVP算法主要由以下基本步驟完成:首先,使用關(guān)鍵字val定義一個(gè)可變長(zhǎng)數(shù)組doubleCol用于存放特征對(duì)的計(jì)算結(jié)果。其次,使用map映射操作將RDD數(shù)據(jù)datapre轉(zhuǎn)換為鍵值對(duì)的形式,即pair((x(m);x(n));1)。值得注意的是,((x(m);x(n))是特征對(duì)m和n的取值;1表示特征對(duì)的值出現(xiàn)一次,并且記錄每一對(duì)特征對(duì)取值的整體出現(xiàn)情況。然后,使用關(guān)鍵字val定義另一個(gè)可變長(zhǎng)數(shù)組singleCol用于存放單個(gè)特征的計(jì)算結(jié)果,由于在計(jì)算單特征值時(shí)容易出現(xiàn)數(shù)據(jù)傾斜,為了緩解數(shù)據(jù)傾斜問(wèn)題,最后需要對(duì)單個(gè)特征的取值進(jìn)行數(shù)據(jù)虛擬劃分。
具體算法如下:
算法1:DVP算法
輸入:數(shù)據(jù)集DS(nobjects ×mfeatures),由數(shù)據(jù)集生成的名為 datapre的RDD
輸出:兩個(gè)變長(zhǎng)數(shù)組
(1) val doubleCol = new Array [ArrayBuffer [Map [(String, String), Long] ] ](dimension) //關(guān)鍵字val定義了一個(gè)可變長(zhǎng)度數(shù)組,即doubleCol
(2) for (m= 0;m≤dimension;m++)
(3) for (n= 0;n≤dimension;n++)
(4) doubleCol(m)(n)+ = datapre:map(x≥((x(m);x(n)); 1))>.countByKey()>.toMap //將RDD數(shù)據(jù)的datapre轉(zhuǎn)換為pair ((x(m); >x(n));>1)使用映射轉(zhuǎn)換,并計(jì)算特征對(duì)取值的整體出現(xiàn)情況
(5) end for
(6) end for
(7)val singleCol = ArrayBuffer[Map[String,Long]]() //關(guān)鍵字val定義了一個(gè)可變長(zhǎng)度數(shù)組,即singleCol
(8) for (k= 0;k≤dimension;k++)
(9) singleCol+= datapre.map
(10) val random:Random = new Random()
(11) val prefix:Int = random.nextInt(10)
(12) prefix+-+x(k),1)).reduceByKey(-+-).map (line ≥(line.-1.split("-")(1), line.-2)).reduceByKey (-+-).collectAsMap().toMap // 數(shù)據(jù)虛擬劃分
(13) end for
4 實(shí)驗(yàn)結(jié)果及分析
4.1 實(shí)驗(yàn)環(huán)境
DVP算法在一個(gè)配備了24個(gè)節(jié)點(diǎn)的Spark集群中實(shí)現(xiàn)并驗(yàn)證,每個(gè)節(jié)點(diǎn)都有一個(gè)Intel處理器(即,E5-1620 v2系列3.7 GHz),4芯16 GB RAM。主節(jié)點(diǎn)硬盤(pán)配置為500 GB;其它節(jié)點(diǎn)的磁盤(pán)容量是2 TB。集群中的所有數(shù)據(jù)節(jié)點(diǎn)都通過(guò)千兆以太網(wǎng)連接;使用SSH協(xié)議保證節(jié)點(diǎn)之間的通信。我們?cè)赟park的standalone模式下實(shí)現(xiàn)了DVP算法。
在DVP實(shí)現(xiàn)中使用的編程語(yǔ)言是Scala,這是一種在Java虛擬機(jī)(JVM)上運(yùn)行的函數(shù)式面向?qū)ο笳Z(yǔ)言。Scala無(wú)縫集成了現(xiàn)有的Java程序。利用集成開(kāi)發(fā)環(huán)境IntelliJ IDEA開(kāi)發(fā)了DVP算法。
表1中列出了DVP算法中所用到的Spark集群的配置情況。
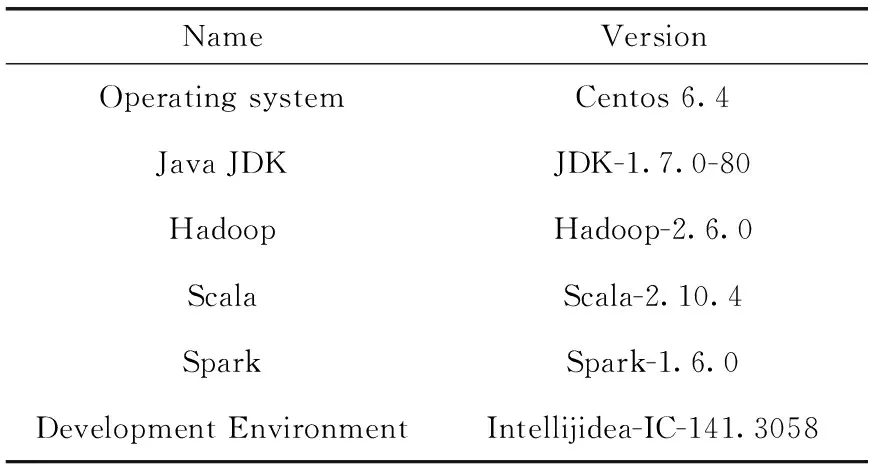
表1 Spark集群中的軟件配置
4.2 人工數(shù)據(jù)集
DVP使用人工合成類(lèi)別數(shù)據(jù)集來(lái)進(jìn)行性能評(píng)估。為了評(píng)估DVP算法,構(gòu)造了兩種類(lèi)型的合成數(shù)據(jù)集:均勻分布數(shù)據(jù)集和正態(tài)分布數(shù)據(jù)集。通過(guò)以下兩個(gè)步驟生成數(shù)據(jù)集。首先,創(chuàng)建一個(gè)相對(duì)較小的類(lèi)別屬性數(shù)據(jù)集。接下來(lái),不斷復(fù)制第一步中創(chuàng)建的數(shù)據(jù)集,以擴(kuò)大數(shù)據(jù)集的大小。合成數(shù)據(jù)集包含100個(gè)特征,這些數(shù)據(jù)集的大小分別為8 GB、16 GB、24 GB和32 GB。數(shù)據(jù)集見(jiàn)表2。
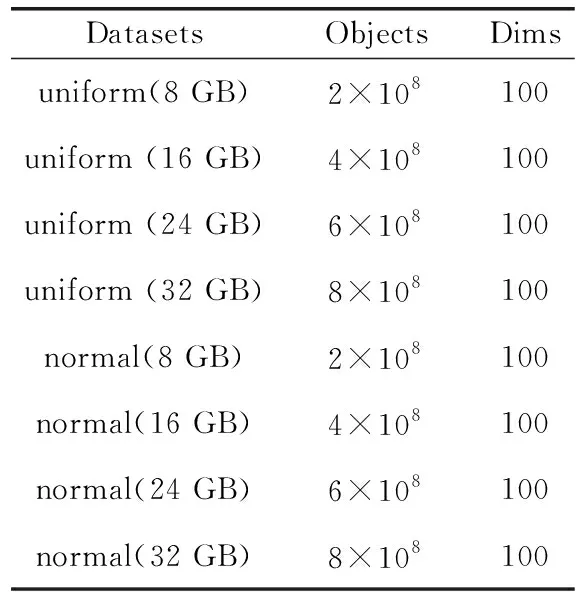
表2 人工合成數(shù)據(jù)集
4.3 比較算法DEFH
DEFH是使用最廣泛的哈希算法,是Spark中的一種默認(rèn)機(jī)制。當(dāng)鍵值呈現(xiàn)均勻分布時(shí),可以獲得較好的性能。
4.4 實(shí)驗(yàn)分析
(1)不同數(shù)據(jù)大小下的執(zhí)行時(shí)間:圖3為DVP和DEFH算法處理不同數(shù)據(jù)大小的均勻分布數(shù)據(jù)和正態(tài)分布數(shù)據(jù)所使用的運(yùn)行時(shí)間。分別將數(shù)據(jù)大小設(shè)置為8 GB、16 GB、24 GB和32 GB。計(jì)算節(jié)點(diǎn)的數(shù)量配置為24個(gè)。
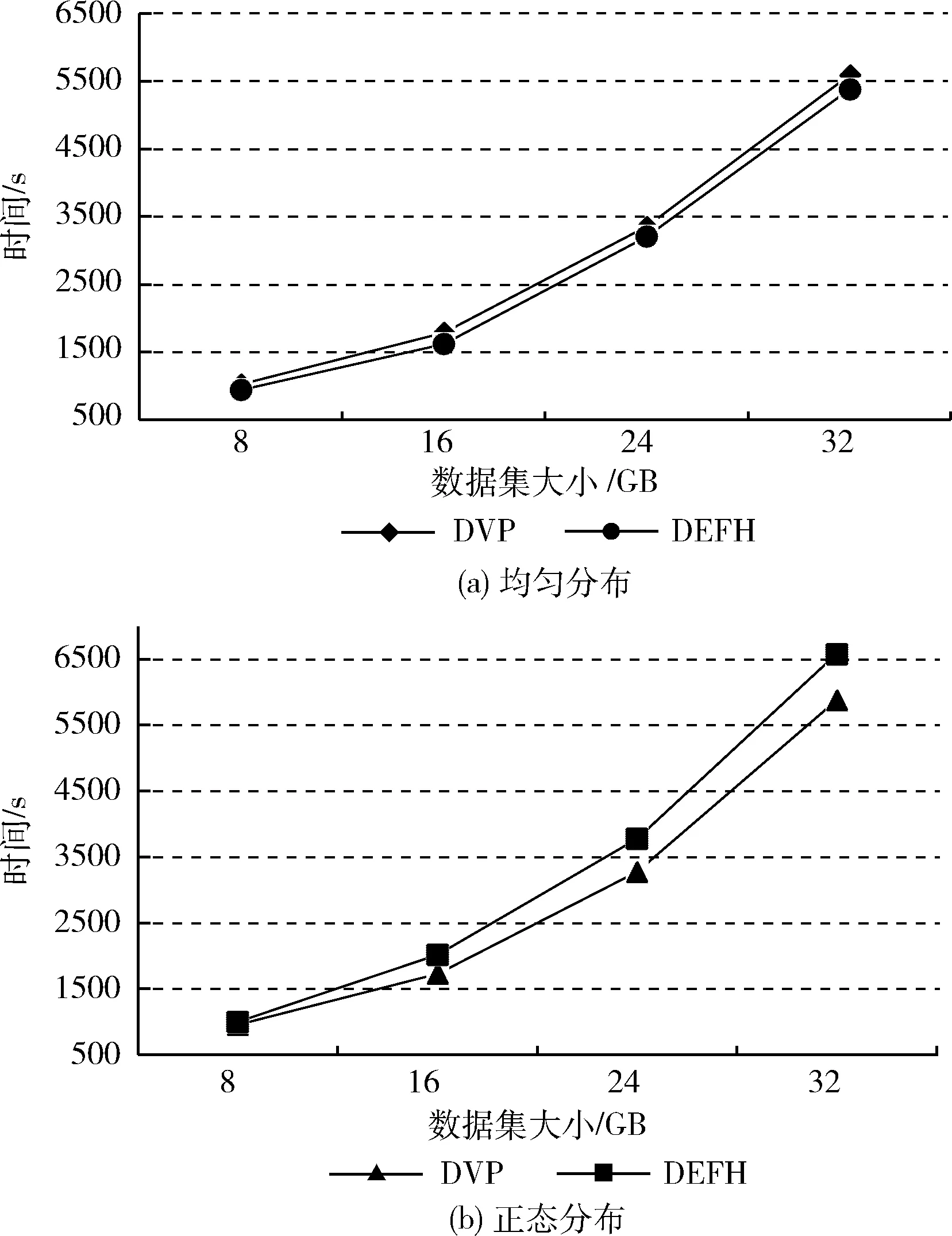
圖3 不同數(shù)據(jù)大小下均勻分布和正態(tài) 分布數(shù)據(jù)的執(zhí)行時(shí)間
由圖3(a)可以看出,在分布均勻的數(shù)據(jù)集中,由于虛擬分區(qū)的副作用,DVP算法的運(yùn)行時(shí)間比DEFH稍長(zhǎng)。然而,從圖3(b)可以看出,對(duì)于正態(tài)分布的數(shù)據(jù)集,DVP算法優(yōu)于DEFH。這是預(yù)期的結(jié)果,因?yàn)檎龖B(tài)分布數(shù)據(jù)集包含了分布不均勻的數(shù)據(jù),導(dǎo)致了數(shù)據(jù)傾斜,從而耗費(fèi)了時(shí)間。而由虛擬分區(qū)支持的DVP算法可以很好地處理傾斜數(shù)據(jù)。
另外,從圖3(a)和圖3(b)還可以看出,增加數(shù)據(jù)量會(huì)導(dǎo)致所有算法的運(yùn)行時(shí)間增加。直觀地說(shuō),這是因?yàn)樘幚泶笠?guī)模數(shù)據(jù)需要更長(zhǎng)的時(shí)間。
(2)不同計(jì)算節(jié)點(diǎn)下的執(zhí)行時(shí)間:圖4展示了DVP和DEFH算法在不同數(shù)量的計(jì)算節(jié)點(diǎn)上處理均勻分布數(shù)據(jù)和正態(tài)分布數(shù)據(jù)所使用的時(shí)間。節(jié)點(diǎn)的數(shù)量分別配置為4、8、16和24。數(shù)據(jù)大小設(shè)置為8 GB。圖4(a)顯示,由于虛擬分區(qū)的開(kāi)銷(xiāo),我們的DVP算法在均勻分布數(shù)據(jù)中的運(yùn)行時(shí)間要比DEFH的運(yùn)行時(shí)間長(zhǎng)。這一趨勢(shì)與圖3(a)所示一致。圖4(b)顯示,在不均勻分布的情況下,正態(tài)分布數(shù)據(jù)集中DVP算法的性能要明顯優(yōu)于DEFH。DVP在DEFH上的性能改進(jìn)歸功于數(shù)據(jù)虛擬劃分,它有效地緩解了數(shù)據(jù)的傾斜。同樣,這些結(jié)果和圖3(b)所描述是一致的。
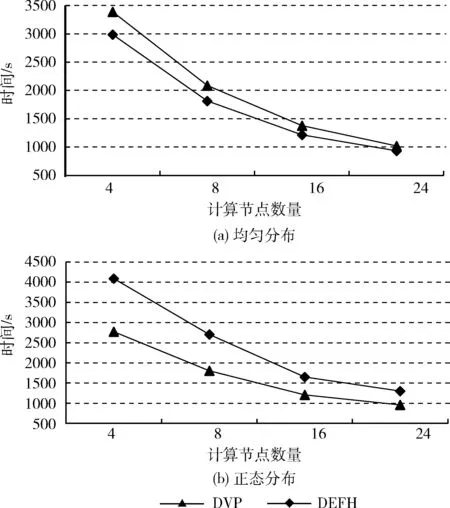
圖4 不同數(shù)量節(jié)點(diǎn)下均勻分布和正態(tài) 分布數(shù)據(jù)的執(zhí)行時(shí)間
另外,從圖4(a)和圖4(b)還可以看出,隨著計(jì)算節(jié)點(diǎn)數(shù)量的不斷增加,兩個(gè)算法的運(yùn)行時(shí)間都有所減少。這主要是因?yàn)榧河?jì)算能力的不斷增加。
(3)數(shù)據(jù)傾斜度的影響:由于均勻分布數(shù)據(jù)集中不會(huì)發(fā)生數(shù)據(jù)傾斜,因此選擇正態(tài)分布數(shù)據(jù)集進(jìn)行實(shí)驗(yàn)。從處理時(shí)間的角度對(duì)數(shù)據(jù)傾斜度的影響進(jìn)行了評(píng)價(jià)。
圖5顯示了不同數(shù)據(jù)傾斜度下DVP和DEFH算法的處理時(shí)間,傾斜度從1到3不等,增量為0.5。我們觀察到,DVP算法的處理時(shí)間對(duì)數(shù)據(jù)傾斜度的敏感性小于DEFH。例如,當(dāng)我們將傾斜度從1.5提高到3時(shí),DVP和DEFH算法的處理時(shí)間分別增加了7.2%和28.4%。實(shí)驗(yàn)結(jié)果表明,DVP算法利用數(shù)據(jù)虛擬劃分有效地緩解了數(shù)據(jù)傾斜帶來(lái)的性能問(wèn)題。因此,在不平衡數(shù)據(jù)集中,DVP算法優(yōu)于DEFH。在較高的數(shù)據(jù)傾斜度下,DVP算法對(duì)數(shù)據(jù)傾斜的改善更為顯著。

圖5 數(shù)據(jù)傾斜度對(duì)DVP和DEFH處理時(shí)間的影響
(4)Shuffling-Cost分析:通過(guò)改變計(jì)算節(jié)點(diǎn)的數(shù)量來(lái)比較DVP和DEFH算法的Shuffling-Cost成本。以節(jié)點(diǎn)的shuffle-write-size作為對(duì)算法的Shuffling-Cost進(jìn)行監(jiān)控。以正態(tài)分布數(shù)據(jù)集(8 G)為例,圖6是兩個(gè)算法Shuffling-Cost對(duì)比。
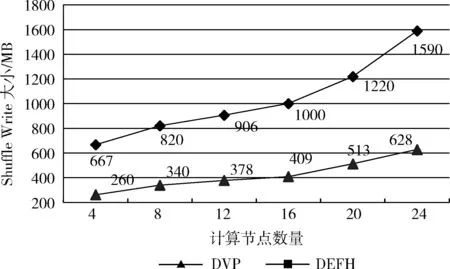
圖6 不同數(shù)量計(jì)算節(jié)點(diǎn)上的DVP和DEFH的 Shuffling-Cost
顯而易見(jiàn),所有測(cè)試用例中DVP算法的shuffle-write-size都明顯小于DEFH。更重要的是,隨著計(jì)算節(jié)點(diǎn)數(shù)量的不斷增加,兩種解決方案之間的shuffle-write-size差距也在擴(kuò)大。DEFH依賴(lài)于Spark的默認(rèn)哈希分區(qū),導(dǎo)致任務(wù)頻繁地跨多個(gè)節(jié)點(diǎn)訪問(wèn)數(shù)據(jù)。例如,當(dāng)節(jié)點(diǎn)數(shù)量從4個(gè)更改為24個(gè)時(shí),DEFH算法的shuffle-write-size從667.0 MB上升到1590.0 MB。與DEFH算法不同的是,DVP算法利用了數(shù)據(jù)虛擬劃分技術(shù)來(lái)減少Spark環(huán)境中的數(shù)據(jù)傳輸量。因此,DVP算法的shuffle-write-size僅僅從260.0 MB跳到628.0 MB。就shuffling-cost而言,這比DEFH的情況要好得多。
(5)可擴(kuò)展性分析:在這組實(shí)驗(yàn)中,通過(guò)增加計(jì)算節(jié)點(diǎn)的數(shù)量(分別設(shè)置為4、8、16和24)和調(diào)節(jié)數(shù)據(jù)集大小(配置分別為8 GB、16 GB、24 GB和32 GB),對(duì)DVP算法進(jìn)行可擴(kuò)展性分析,評(píng)估DVP算法在集群系統(tǒng)中處理大規(guī)模數(shù)據(jù)的能力。
圖7(a)顯示了Spark集群中節(jié)點(diǎn)數(shù)量對(duì)并行互信息計(jì)算時(shí)間的影響。由圖7(a)可以看出,隨著計(jì)算節(jié)點(diǎn)數(shù)量的增加,DVP算法的執(zhí)行時(shí)間明顯減少。大數(shù)據(jù)集(如32 GB)的下降趨勢(shì)非常明顯。當(dāng)數(shù)據(jù)集很小(例如4 GB)時(shí),集群擴(kuò)展性能提高很微弱。結(jié)果表明,DVP是一種對(duì)大數(shù)據(jù)集具有高擴(kuò)展性的并行計(jì)算方法。
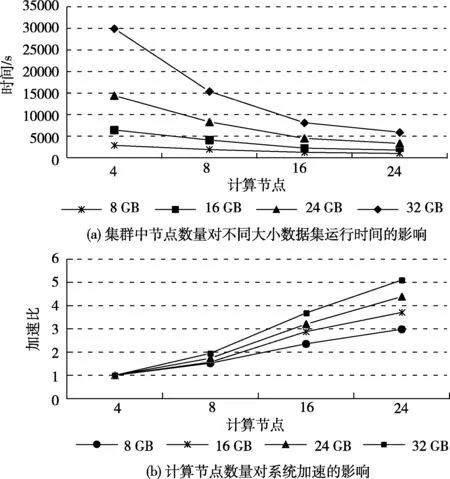
圖7 DVP的可擴(kuò)展性分析
圖7(b)展示了計(jì)算節(jié)點(diǎn)數(shù)量對(duì)系統(tǒng)加速的影響。從圖7(b)可以看出,對(duì)于大多數(shù)數(shù)據(jù)集來(lái)說(shuō),DVP的加速率接近線性。例如,在32 GB的情況下,DVP的加速性能幾乎與線性性能相當(dāng)。結(jié)果表明,我們的并行計(jì)算算法能夠保持大規(guī)模高維類(lèi)別數(shù)據(jù)集的計(jì)算性能。
上述DVP的高可擴(kuò)展性主要?dú)w功于以下幾個(gè)因素。首先,并行互信息計(jì)算的時(shí)間在很大程度上取決于任意兩個(gè)特征之間的互信息計(jì)算,這種互信息計(jì)算時(shí)間與分配給節(jié)點(diǎn)的數(shù)據(jù)對(duì)象數(shù)量成正比。其次,所有計(jì)算節(jié)點(diǎn)都獨(dú)立地并行計(jì)算。最后,由于數(shù)據(jù)虛擬劃分,DVP在所有節(jié)點(diǎn)之間保持了良好的負(fù)載平衡性能。
5 結(jié)束語(yǔ)
本文基于Spark平臺(tái)開(kāi)發(fā)了DVP算法,在大規(guī)模類(lèi)別數(shù)據(jù)的背景下并行計(jì)算互信息。DVP的核心是數(shù)據(jù)虛擬分區(qū)方案。更具體地說(shuō),虛擬分區(qū)技術(shù)緩解了shuffle過(guò)程中出現(xiàn)的數(shù)據(jù)傾斜問(wèn)題。最后在一個(gè)24節(jié)點(diǎn)驅(qū)動(dòng)的Spark集群上采用人工合成類(lèi)別數(shù)據(jù)集驗(yàn)證了DVP算法。
大量的實(shí)驗(yàn)結(jié)果表明,該算法在效率和負(fù)載均衡等方面優(yōu)于Spark集群默認(rèn)的DEFH算法。此外, 在Spark處理大型類(lèi)別數(shù)據(jù)集時(shí),DVP能夠很好地減輕數(shù)據(jù)傾斜,從而優(yōu)化網(wǎng)絡(luò)性能。
在未來(lái)的工作中,將重點(diǎn)從內(nèi)存資源的角度優(yōu)化shuffle性能。當(dāng)數(shù)據(jù)分布變得不均勻時(shí),分配給分區(qū)的數(shù)據(jù)量就不平衡。因此,任務(wù)所需的內(nèi)存空間本質(zhì)上是不同的。如果給每個(gè)任務(wù)分配固定比例的內(nèi)存空間,任務(wù)中頻繁的內(nèi)存溢出將是不可避免的。這樣的內(nèi)存資源問(wèn)題會(huì)對(duì)Spark的整體性能產(chǎn)生負(fù)面影響。打算研究一種分配內(nèi)存資源的方法,以進(jìn)一步優(yōu)化所有任務(wù)之間的shuffle進(jìn)程。該技術(shù)有望從內(nèi)存計(jì)算的角度提高Spark應(yīng)用程序的性能。

