基于遷移子空間的半監督領域自適應方法

陶 洋，楊 雯，翁 善，林飛鵬

(重慶郵電大學 通信與信息工程學院，重慶 400065)

0 引 言

在實際應用中，傳統機器學習算法面臨著缺乏標簽樣本的困境。近年來，遷移學習和領域自適應方法得到廣泛研究，這類方法將源域(訓練集)豐富的知識遷移到目標域(測試集)來解決缺乏標簽問題[1-3]。基于特征表達的領域適配方法通過原始空間或投影空間中的特征表示實現源域和目標域之間的對齊[4-6]。Zhang等[7]提出了隱稀疏域遷移模型，在域之間聯合學習稀疏編碼和最優子空間，挖掘子空間中源域和目標域共有的隱藏結構。B.Sun等[8]提出子空間分布對齊法，在子空間對齊的基礎上增加了概率分布自適應，對源域和目標域進行二階特征變換，實現源域和目標域數據對齊。然而這些方法都沒有很好地利用樣本的標簽信息提高分類性能，因此一些方法結合了分類器設計和特征表示算法的優點，利用了樣本的標簽信息增強了模型的判別性[9-11]，還有一些方法利用樣本標簽，挖掘了重構矩陣所包含的樣本之間的類內與類間信息，提高模型的分類性能[12]。本文中，主要研究了基于特征表示的領域自適應，并提出了基于遷移子空間的半監督領域自適應方法(semi-supervised domain adaptation via transfer subspace，SSDTS)。該方法利用類別標簽先驗信息，進一步分析同類樣本之間的相似性和異類樣本之間的差異性，得到鑒別性共享子空間和具有塊對角結構的類重構矩陣，最終提高模型的分類性能。

1 相關理論

1.1 子空間學習

子空間學習(subspace learning，SL)是基于某一特定準則，將原始高維的樣本變換到低維、有意義的子空間中，其目的是為了找出數據的內在結構[13,14]，得到能反映原始樣本分類本質的低維特征。子空間學習的任務有兩個，一是尋找針對模式最具鑒別性的描述，用較低維度的特征描述原始樣本并保留分類所需的鑒別信息。二是原始數據進行維度約減后，能減少后續運算的計算量，提高運算速度。

1.2 稀疏表示和低秩表示

子空間學習方法中的兩大重要理論包括稀疏表示(sparse representation，SR)和低秩表示(low-rank representation，LRR)。其中稀疏問題來自域信號處理領域的壓縮感知(compressive sensing，CS)。稀疏性是指為了更好地對復雜的多維圖像進行描述，可以將圖像信號看成是由適當選取的一組過完備基中少數幾個基的線性組合，即用最少基的線性組合來表達圖像信號，得到信號在這組基上的稀疏表示。稀疏表示能從大量樣本中發掘數據的內在結構，具有良好的自適應性和鑒別性，然而其在求解過程中缺乏對整體樣本結構的全局約束，因此難以有效發掘樣本的全局結構。矩陣的稀疏性可以通過秩來度量，具有很強的全局約束。低秩表示系數矩陣可以增強對噪聲的抵抗能力。當數據來自多個獨立子空間時，低秩表示能夠準確發現數據本身蘊含的多子空間結構。此時獲得的低秩表示系數矩陣會呈現塊對角形式，每個塊對應每個子空間。

2 基于遷移子空間的半監督領域自適應方法

2.1 方法概述

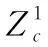
圖1 SSDTS算法整體框架

2.2 問題建模

遷移子空間學習的目標是找到一個投影矩陣，通過投影矩陣將源域數據和目標域數據投影到共享子空間，在子空間中源域和目標域樣本分布大致相同。本文提出的方法假設在共享子空間中目標域數據可以由源域數據線性重構，可形式化的表示為

(1)

其中，φ(·)是原始特征空間到再生希爾伯特空間的非線性映射，P是投影矩陣，Z是重構矩陣。稀疏表示是局部約束，能夠發現數據間的局部線性關系，對重構矩陣Z施加稀疏約束，不僅可以保留數據的局部結構，而且使每個目標域樣本可以被少量源域樣本更好地重構。低秩性不僅有利于揭示塊對角結構，還能夠保留數據的全局結構。對重構矩陣Z施加低秩約束使矩陣具有塊對角結構，獲得源域樣本和目標域樣本的一致表示，使源域樣本和目標域樣本在共享子空間中可以很好地對齊。對重構矩陣Z同時施加稀疏和低秩約束后可得

(2)

(3)

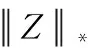
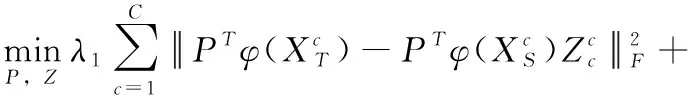
(4)

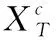
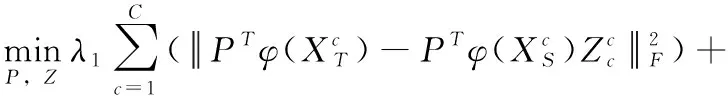
(5)

利用樣本的先驗類別信息，將嚴格的二值標簽矩陣松弛為變量矩陣，增大投影后不同類樣本之間的距離，挖掘樣本內蘊含的鑒別信息，加強投影后子空間中樣本的判別性，以此提高分類性能。式(5)可以表示為

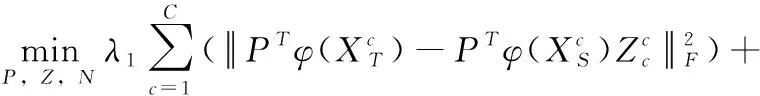
(6)

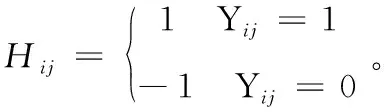
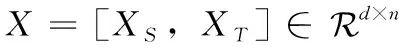
圖嵌入方法能夠保證相同類的樣本在轉換后能緊密地聚集在一起，避免過擬合。引入了類緊致圖(class compactness graph，CCG)作為正則項。在類緊致圖中，同一個類的兩個不同樣本通過無向邊連接，因此類緊致圖的權重定義為

(7)

其中，σ表示核參數，可以通過下式(8)使得轉換后的同類樣本緊密聚集在一起

(8)

其中，fi=xiP表示轉換后的第i個訓練樣本xi，L表示拉普拉斯圖，定義為L=D-W，D為對角矩陣，對角元素為Dij=∑jWij。聯合式(6)和式(8)，最終定義的目標函數如下

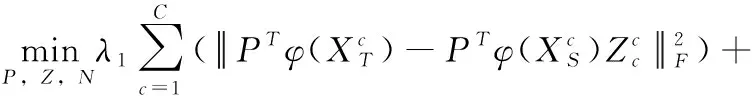
(9)

2.3 模型優化求解

(10)

其中，k(·)是核函數，滿足條件k(xi,xj)=〈φ(xi),φ(xj)〉=φ(xi)Tφ(xj)。令K=φ(X)Tφ(X)，Ks=φ(X)Tφ(Xs)和Kt=φ(X)Tφ(Xt)表示核格列姆矩陣。通常最優投影矩陣P可以直觀地表示為φ(X)的線性組合，即P=φ(X)Φ。將其代入到式(10)中，可以得到

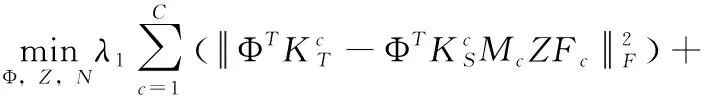
(11)

為了求解式(11)，采取了變量交替優化策略，即固定其它變量來迭代更新每個變量。通過對重構矩陣Z引入兩個輔助變量J和T，將引入新輔助變量的最小化問題重新寫成

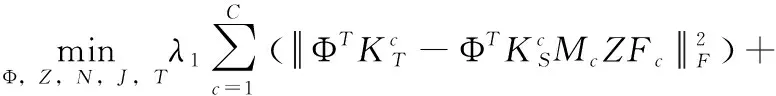
(12)

通過增強的拉格朗日乘數(augmented lagrange multiplier，ALM)，上述式(12)可以轉換為以下最小化問題

(13)

其中，Y1和Y2是拉格朗日乘子，μ>0是懲罰參數。上述式(13)問題可以通過不精確拉格朗日法(inexact augmented lagrange multiplier，IALM)解決，具體步驟如下所示：

步驟1更新Φ，固定變量Z，J，T和N，解決優化式(14)來更新Φ

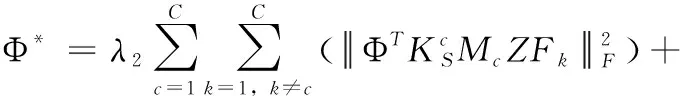
(14)

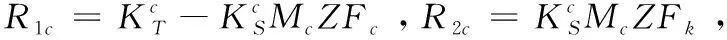
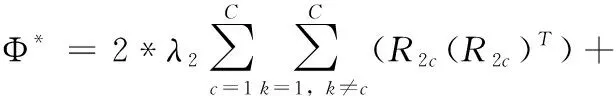
(15)

其中，式(15)中的A=Y+B⊙M。

步驟2更新J，去掉與J無關的項后，式(13)可以重新寫成下列形式

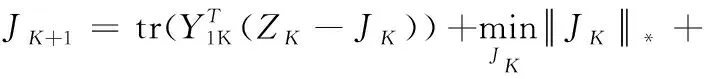
(16)

式(16)可以進一步寫成下列形式

(17)

通過奇異值閾值(SVT)算子可以有效地解決式(17)。

步驟3更新T，去掉與T無關的項后，式(13)可以重新寫成下列形式

(18)

式(18)可以進一步寫成下列形式

(19)

利用收縮算子對式(19)求解，結果如下所示

(20)

步驟4更新Z，去掉與Z無關的項后，式(13)可以重新寫成式(21)形式

(21)

通過式(21)很難得到Z的封閉解，根據梯度下降算子，可以得到解ZK+1的表達式

(22)

其中，Z的導數可以表示為式(23)

(23)

步驟5更新N，可以通過解決式(24)問題更新N

(24)

令ΦTK-Y=I，考慮N的第(i,j)項Nij，可以得到下式

(25)

Nij的最優解是

Nij=max(IijHij,0)

(26)

因此，N的最優解也可以改寫為

N=max(I⊙H,0)

(27)

表1中詳細總結了所提算法的迭代優化過程。

表1 SSDTS算法迭代流程

3 實驗驗證與結果分析

本文使用的基準數據集分別是：Office、Caltech256、COIL、MNIST和USPS數據集。為了驗證本論文提出算法的性能，在上述基準數據集上進行實驗，并與多個相關的經典領域自適應算法，即SGF、GFK、JDA、LTSL、SA、LSDT、CORAL、LRSR算法進行對比。本文提出的SSDTS算法選擇K-最近鄰分類器作為分類器。由于SSDTS算法是半監督遷移學習算法，目標域中存在部分標簽，故使用源域樣本與少量有標簽目標域樣本訓練分類器，然后使用無標簽目標域樣本測試分類效果。文中所有實驗均重復了20次，最后記錄平均分類正確率。

3.1 數據集介紹

Office數據集是可視化領域適配的基準數據，該數據集包括了來自亞馬遜(Amazon)、數碼單反(DSLR)和網絡攝像頭(Webcam)3個域中的常見對象類別。在Office數據集中，每個域包含31個不同的對象，共有4652張圖像。Caltech256數據集包含了256個類別，共有30 607幅圖像。Office和Caltech數據集的部分圖像樣例如圖2所示。將Amazon用符號A表示，DSLR用符號D表示，Webcam用符號W表示，Caltech256用符號C表示，利用這4個域中共有的10個類別進行實驗。任意選取兩個域作為源域和目標域進行實驗，一共可以得到12組相關實驗。根據文獻[12]中的設置，實驗中，當Amazon作為源域時，則從每類中隨機選擇20個樣本作為源域數據集，如果是DSLR、Webcam和Caltech256作為源域，則從每類中隨機選擇8個樣本作為源域數據集。當4個域的樣本作為目標域時，從每類中隨機選擇3個樣本作為目標域數據集，剩下的作為測試數據集。對于Office和Caltech256數據集采用SURF特征和DeCAF6兩種特征進行實驗。

圖2 Office和Caltech256數據集圖像樣例

USPS和MNIST數據集都包含10個類，分別是數字0-9，兩個數據集的部分樣例如圖3所示。USPS數據集中，包含訓練圖像7291張和測試圖像2007張，共有9298張圖像。MNIST數據集中，包含60 000張訓練圖像和10 000張測試圖像，共有70 000張圖像。在實驗中，從兩個數據集中隨機選擇10 000張圖像分別作為實驗中的源域和目標域，一共可以得到2組相關實驗。當USPS和MNIST數據集作為源域時，則從每類中隨機抽取100個樣本作為源域數據集，當USPS和MNIST數據集作為目標域時，從每類中隨機抽取10個樣本，共100個樣本作為目標域數據集，其余未抽取樣本作為測試數據集。

圖3 USPS和MNIST數據集樣例

COIL-20數據集包含了20類對象，共1440張圖片。該數據集中的部分樣例如圖4所示。

圖4 COIL數據集樣例

在本次實驗中，數據集被劃分為兩個子集C1和C2，兩個子集各有720張圖像。將C1和C2交替作為源域和目標域可以得到2組實驗。當C1和C2子集作為源域時，選取子集中的所有樣本作為源域數據集，當C1和C2子集作為目標域時，從所有類別的樣本中隨機抽取270個樣本作為目標域數據集，剩余未抽取樣本作為測試數據集。

3.2 實驗結果對比

在Office+Caltech256(SURF)數據集上進行分類實驗的結果具體見表2，在Office-Caltech256(DeCAF6)數據集上進行分類實驗的結果見表3，在USPS和MNIST數據集上進行分類實驗的結果見表4，在COIL數據集上進行分類實驗的結果見表5。下面4個表中部分實驗結果引自文獻[12]和文獻[15]，粗體數字為每個任務的最優分類結果。

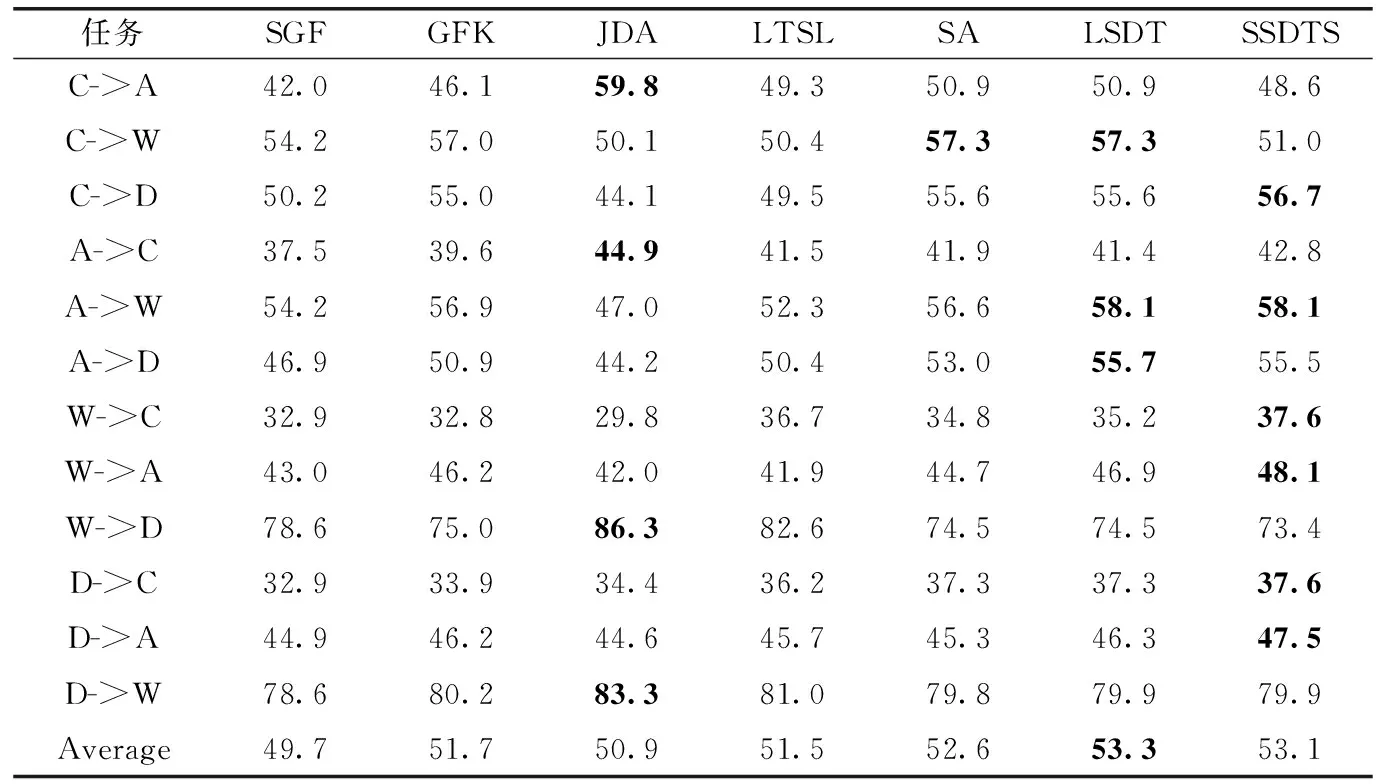
表2 在Office+Caltech256數據集(SURF)上的分類結果

綜合以上各組實驗結果可以看出，SSDTS算法在上述4個數據集共28個任務中，有21個任務的分類正確率超過了其它對比算法。除了Office-Caltech256數據集(SURF)，SSDTS算法在其余的數據集中各任務的平均分類正確率均超過了其它算法，驗證了在對齊領域總體分布時考慮樣本的先驗類別信息有利于提高分類正確率。

如表4所示，在USPS和MNIST數據集上，任務“M->U”的分類準確率都不同程度高于任務“U->M”，這是因為MNIST數據集規模大于USPS數據集，提供的分類信息更加充足。如表5所示，在COIL數據集中的兩個任務都取得了最優分類結果，平均分類準確率達到了94.3%，比最優對比方法LRSR提高了2.6%。如表3和表4所示，在(DeCAF6)Office-Caltech256數據集、USPS和MNIST數據集上的任務中，SSDTS算法的分類準確率均高于LRSR算法，這表明利用樣本類標簽，逐類考慮同類樣本的相似性和異類樣本的差異性，挖掘重構矩陣中所蘊含的判別信息的有效性。

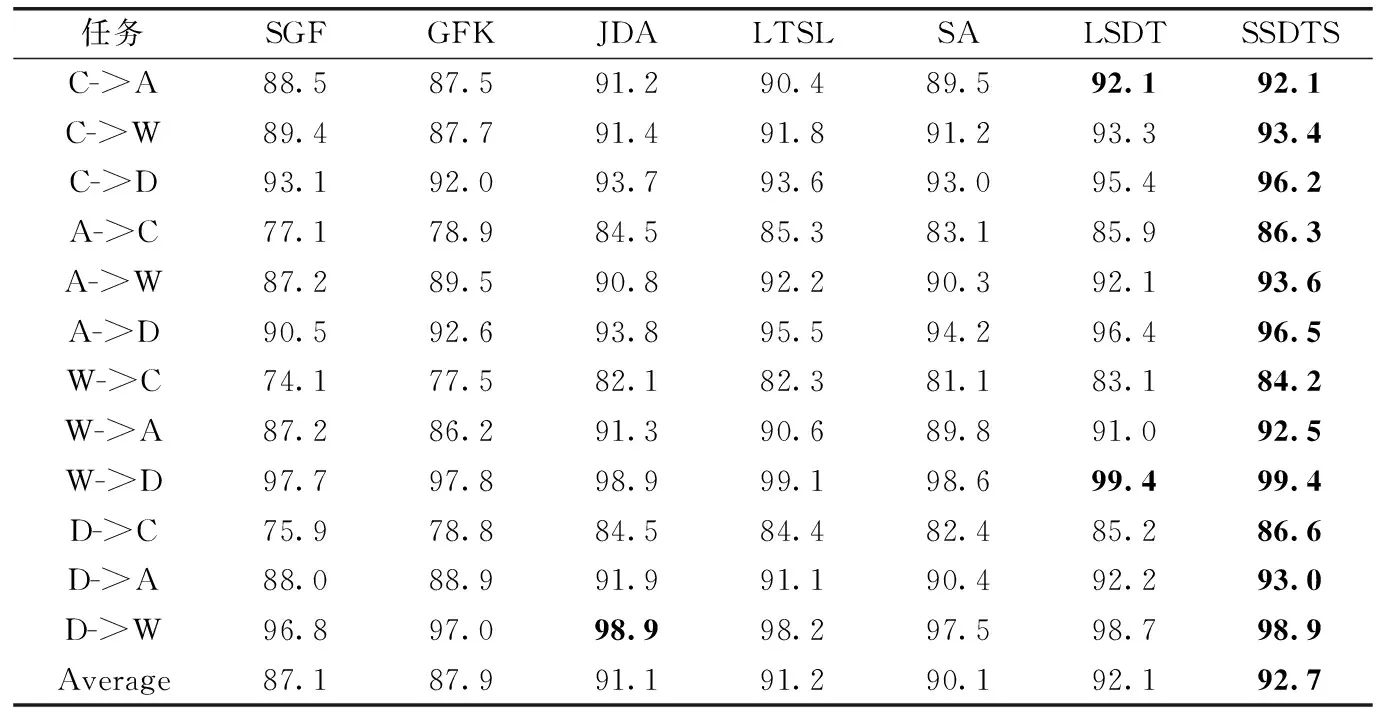
表3 在Office+Caltech256數據集(DeCAF6)上的分類結果

表4 在USPS和MNIST數據集上的分類結果

表5 在COIL數據集上的分類結果

3.3 重構矩陣可視化

引入樣本的類標簽信息，獲得具有塊對角結構的類重構矩陣，可以進一步挖掘樣本中蘊含的鑒別信息，揭示同類樣本之間的相似性和不同類樣本之間的差異性，有助于提高分類性能。如圖5所示，在Office-Caltech256(DeCAF6)數據集的實驗中，對重構矩陣Z進行可視化，可以看到重構矩陣Z呈現出塊對角結構，也就是說目標數據中的第c類樣本可以很好地由同類的源域數據線性表示。

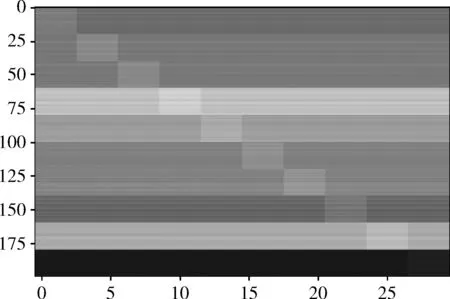
圖5 重構矩陣可視化

3.4 參數敏感性分析

如式(10)所示，SSDTS算法模型有λ1和λ2兩個參數。為了驗證參數的有效性，本節實驗測試了λ1和λ2兩個參數不同值的組合下對SSDTS算法性能的影響。在Office-Caltech256(DeCAF6)數據集的A->D任務和USPS-MNIST數據集的M->U任務上進行實驗。參數λ1和λ2的取值范圍設置為{10-3,10-2,10-1,1,101,102}。不同參數組合對分類正確率的影響如圖6所示。可以看出，不同的分類任務中對于參數λ1、λ2取值的敏感度不同。在A->D任務中，當參數λ1=0.01，λ2=0.1時，得到最大分類準確率，在M->U任務中，當參數λ1=100，λ2=10時，得到最大分類準確率。表明在不同跨域任務中，相同類之間的類內依賴和不同類之間的類間獨立并不是同等重要。

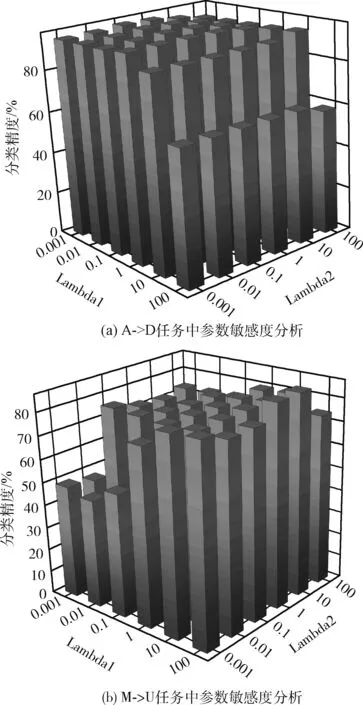
圖6 重構矩陣可視化

3.5 算法運行時間對比

本節對比了SSDTS算法與GFK、JDA、LSDT和LTSL算法的運行時間。所有的測試都在一臺CPU為Intel 1.8 Ghz雙核處理器、內存為8 GB的計算機上完成，軟件平臺選定為MATLAB R2018b。本節實驗在Office-Caltech256(DeCAF6)數據集的W->D任務和COIL數據集的C1->C2任務上進行實驗，各個算法的執行時間見表6。其中LSDT算法的運行時間最短，其次是SSDTS算法。LTSL算法的運行時間最長，這是因為該算法的收斂速度相較于其它算法較慢。

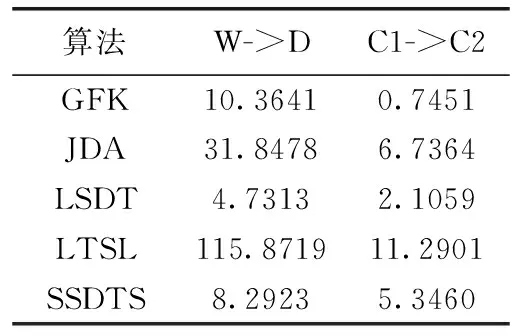
表6 算法運算時間對比/s

4 結束語

針對領域自適應在跨領域圖像識別中存在領域偏差、數據特征分布不一致的問題，本文提出了一種基于遷移子空間的半監督領域自適應方法(SSDTS)，通過投影矩陣將源域樣本和目標域樣本投影到低維共享子空間中，使得目標域樣本被同類別源域樣本線性重構，從而減少源域和目標域之間的差異。此外，為充分發掘同類樣本之間的相似性和異類樣本之間的差異性，利用樣本的標簽信息，得到具有塊對角結構的類重構矩陣。不同于現有的遷移子空間算法，SSDTS模型能夠充分發掘和利用領域間共享標簽先驗知識，同時考慮子空間的判別性以及重構矩陣蘊含的判別信息。在4個領域自適應公開數據集(COIL、USPS-MNIST、Office-Caltech-SURF、Office-Caltech-DeCAF6)上進行實驗，結果表明SSDTS算法優于現有大多數方法。