時間序列模型和LSTM模型在水質預測中的應用研究

胡衍坤，王 寧，劉 樞，姜秋俚，張 楠

1(中國科學院大學，北京 100049)

2(中國科學院 沈陽計算技術研究所，沈陽 110168)

3(遼寧省生態環境監測中心，沈陽 110161)

4(阜新市生態環境保護服務中心，遼寧 阜新 123000)

1 引 言

河流為人類提供了賴以生存的水資源以及水產資源.工業化進程的不斷加快，導致河流水環境受到嚴重破壞.由于河流水質變化與氣候環境、季節更替以及人類活動密切相關，因此河流水質變化呈現出漸變性，非線性，和不確定性等特點[1].水質預測能夠幫助我們更好地了解河流水質變化，從而更好的保護河流水資源.近年來，國內外很多專家學者已針對水質預測做了大量的研究，并取得了較好的成果.傳統的水質預測模型主要包括時間序列模型、灰色系統理論模型、回歸分析模型以及神經網絡模型等.謝建輝等人[2]將ARIMA模型應用到對河流水質主要監測指標化學需氧量和氨氮的預測分析上，較為準確的反映了河流水質的變化趨勢.趙林等人[3]使用BP神經網絡模型對桃林口水庫出庫站7項水質指標進行預測，效果良好.此外，隨著深度學習以及人工智能的快速發展，深度學習模型也越來越多的應用到水質預測研究中.涂吉昌等人[4]應用基于門控型循環神經網絡(GRU)的水質預測模型進行水質預測，顯著提高了水質預測精度.除單一模型外，組合模型也被應用到水質預測的研究.肖榮平等人[5]使用多算法組合的河流水質預測方法進行水質預測，結果表明，組合模型的預測精度顯著提高，能夠更好的適用于復雜水域的水質預測.

ARIMA模型是經典的時間序列預測方法，能夠較好的體現時間序列數據中的線性特征.但是，單一的ARIMA模型對河流水質的非線性變化難以充分有效的處理，需要結合其他算法.在深度學習算法中，LSTM模型由于其特殊的網絡結構，在處理時間序列問題時，比傳統的神經網絡更快更易收斂到最優解，非常適合處理河流水質指標這種時序數據[6].李艷萍等人[7]基于LSTM神經網絡模型較為準確的預測了空氣質量AQI指數.因此，本文建立了ARIMA與LSTM組合模型以及SARIMA與LSTM組合模型進行河流水質預測的研究，并結合實際河流監測數據，分析河流水質變化趨勢.通過比較兩種組合模型對河流水質預測的結果，探究更好的河流水質預測方法，從而更好的保護河流水環境.

2 研究方法

2.1 ARIMA和SARIMA模型

ARIMA模型全稱為差分自回歸移動平均模型(Autoregressive Integrated Moving Average Model,簡記為ARIMA).其中AR是自回歸，p為自回歸項；MA為移動平均，q為移動平均項數；把非平穩的時間序列轉化為平穩序列需要進行d階差分[8].ARIMA模型的一般形式為：

(1)

該模型中包括自回歸AR(p)和移動平均回歸MA(q)兩個過程.在上式中，γi(i=0,1,2,…,p)和θi(i=0,1,2,…,q)是待求參數，p為自回歸過程的滯后階數，q為移動平均過程的滯后階數，μ為常數項系數，t為隨機擾動項序列，通常要求為白噪聲序列，表示為t～WN(0,σt2).ARIMA模型在建模時要求時間序列必須為平穩序列，對于非平穩時間序列數據要進行d階差分后再進行建模.所以，完整的差分自回歸移動平均過程ARIMA(p,d,q)在引入滯后因子后的模型表示為：

(2)

式(2)中L表示滯后因子，其定義為Lnyt=yt-n,(1-L)d為d階差分運算.在建立ARIMA模型時首先要檢測數據的平穩性，對于非平穩時間序列首先進行差分操作，從而確定d的值；然后根據自相關函數(ACF)和偏自相關函數(PACF)的截尾和拖尾性確定p值和q值；然后采用最小二乘法對參數進行估計；最后根據AIC、BIC、殘差檢驗等方式確定最優的p、q值用于模型的訓練.

SARIMA模型是在ARIMA模型的基礎上添加了季節項，主要針對具有季節性或周期性變化的時間序列進行建模[9].SARIMA乘積模型的一般表達形式為：

SARIMA=(p,d,q)×(P,D,Q)s

(3)

式(3)中p為自回歸階數，q為移動平均階數，d為差分階數，P，Q，D分別為季節求和自回歸移動平均模型中的自回歸、移動平均回歸和差分的值，s為季節周期和循環長度.在進行SARIMA建模時，首先進行差分操作，從而確定d和D的值；然后通過ACF來確定p和P的值，通過PACF來確定q和Q的值；然后采用平均法或者移動平均趨勢剔除法對季節性時間序列數據進行分解，從而確定s的值；最后在得到所有參數后，使用參數估計模型進行模型校驗，得到最終模型.

2.2 LSTM模型

圖1 LSTM神經網絡

LSTM模型在RNN的基礎上添加了3個門控結構，分別為“遺忘門”，“輸入門”和“輸出門”[12].LSTM的第一步是確定將從節點狀態中丟棄哪些信息，該判定由稱為“遺忘門”的Sigmoid層決定.它查看ht-1和Xt，并為單元狀態Ct-1中的每個數字輸出0-1之間的數字，0代表“不允許任何量通過”，1代表“允許任何量通過”.Sigmoid函數的輸出值決定前一個狀態的值是否丟棄，表達式為：

ft=σ(Wf·[ht-1,xt]+bf)

(4)

下一步是確定我們將在單元節點狀態中存儲哪些信息，包含兩個部分.“輸入門”的sigmoid函數決定將更新哪些值，tanh函數創建可以添加到狀態的新候選值C～t的向量(一個在-1與1之間的值)并與sigmoid函數的值相乘，最后輸出確定要輸出的那部分.其表達式為：

it=σ(Wi·[ht-1,xt]+bi)

(5)

(6)

最后我們需要通過“輸出門層”來決定輸出的內容.首先運行一個sigmoid層，它決定我們要輸出的單元狀態的哪些部分.然后將單元狀態置于tanh(將值推到介于-1和1之間)并將其乘以sigmoid們的輸出，最終得到將要輸出的部分.其表達式為：

ot=σ(Wo·[ht-1,xt]+bo)

(7)

ht=ot*tanh(Ct)

(8)

2.3 組合預測模型

河流水質預測組合模型設計圖如圖2所示.

圖2 組合模型

2.3.1 數據預處理

數據預處理過程主要處理原始數據中的缺失值以及異常值，首先對數據進行離群點檢測，將異常值視為缺失值，從而使用拉格朗日插值法對缺失值進行填補.

處理措施：提前向海事部門申請《水上水下作業許可證》，并向港航局通航處申請發布關于“水上施工”的航行通告，及時將有關工程情況對相關單位進行宣傳、報道，便于航運單位掌握信息，提高安全航行程度。加強同船閘管理處的聯系與溝通，及時了解開閘通行、停運、高峰期等關鍵時間點，根據船閘管理處相關信息對鋼板樁施工作業時間進行調整，盡量避免在船只通行時進行打樁作業。根據上下游船閘開放時間，盡量減少船只通行對施工造成的干擾，同時最大程度減少施工對通航的影響。在施工區域周圍設置警示線，并在施工區靠航道一側打設一排臨時防護樁，將施工區域進行封閉。

水質監測數據具有線性特征以及非線性特征[13]，將水質數據記為Zt,則可將其分解為線性部分Xt和非線性部分Yt,記為：

Zt=Xt+Yt

(9)

2.3.2 組合模型建模分析

1)時間序列模型建模

(10)

2)LSTM殘差預測

3)模型組合

(11)

2.3.3 模型評價指標

本文對于ARIMA模型和SARIMA模型以及組合模型分別計算模型預測結果的均方誤差(MSE)、均方根誤差(RMSE)[14]和平均絕對百分比誤差(MAPE)，來量化模型預測的準確性.

MSE計算公式為：

(12)

RMSE計算公式為：

(13)

MAPE計算公式為：

(14)

其中pi為模型預測值，xi為訓練集真實值，n為訓練集個數.

3 實驗分析

3.1 實驗環境介紹

本次實驗基于Windows操作系統，使用python語言進行編碼，版本為python3.7，編程工具使用Jupyter Notebook,其中ARIMA與SARIMA模型使用statsmodels包實現，LSTM模型使用TensorFlow框架實現.

3.2 實驗數據

實驗水質數據來源于遼寧省阜新市細河高臺子斷面2013年1月-2020年3月監測數據，選取的污染物指標為化學需氧量(COD)和氨氮(NH3-N).取2013年1月-2018年12月數據作為模型的訓練集，2019年1月-12月數據作為模型的測試集，2020年1月-3月數據作為模型預測的驗證集.

3.3 ARIMA與LSTM組合模型建模實例

在ARIMA模型建模時，首先對時間序列訓練數據進行ADF檢測和白噪聲檢驗，接下來繪制原始時間序列的自相關(ACF)圖和偏自相關(PACF)圖，觀察可知模型p值為1，q值也為1.最后確定模型為ARIMA(1,0,1)，進行模型訓練、檢驗、評估及預測，得到ARIMA的擬合預測序列，然后使用原始數據減去擬合的預測數據得到ARIMA模型預測后的殘差序列,并以滑動窗口的方式將殘差序列切分成n段長度為t的序列，然后應用LSTM模型進行殘差序列模型的訓練和預測得到預測結果，最后將ARIMA模型預測結果與LSTM殘差預測結果相加得到最終預測結果.結果如圖3、圖4所示.

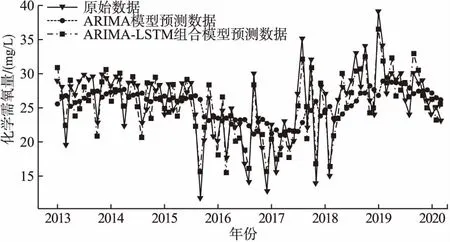
圖3 ARIMA-LSTM模型預測結果

圖4 ARIMA-LSTM模型預測結果

計算可得組合模型化學需氧量預測值均方誤差和均方根誤差分別為5.13和2.26，平均百分比誤差為4.77%.氨氮預測值均方誤差為0.14，均方根誤差為0.19，平均百分比誤差為5.26%，說明ARIMA和LSTM組合模型預測相較于單獨使用ARIMA模型得到了很好的預測結果.

3.4 SARIMA與LSTM組合模型實例

在進行SARIMA建模時需要先提取時間序列數據中的趨勢、季節和隨機效應，從而判斷殘差序列的穩定性以及確定季節項系數.由ARIMA模型建模過程可知，原始化學需氧量和氨氮數據均為平穩數據；根據化學需氧量和氨氮數據自相關圖和偏自相關可知，p值分別為1和2，q值都為1；根據從數據中提取的季節性可知，季節項系數都為12.通過網格搜索并依據AIC準則，可以得到化學需氧量序列SARIMA模型最優參數組合為SARIMA(1,0,1)×(1,0,1,12),氨氮序列SARIMA模型最優參數組合為SARIMA(2,0,1)×(2,0,1,12).進行SARIMA模型訓練和預測得到預測值序列，并計算預測得到的殘差序列，在此基礎上繼續建立SARIMA與LSTM組合模型進行預測，預測結果如圖5、圖6所示.

圖5 SARIMA-LSTM模型預測結果

圖6 SARIMA-LSTM模型預測結果

經計算可得SARIMA和LSTM組合模型對化學需氧量預測值的均方誤差為3.17，均方根誤差為1.37，平均百分比誤差為2.81%，氨氮預測值的均方誤差為0.10，均方根誤差為0.13，平均百分比誤差為3.16%.各模型預測結果對比如圖7、圖8和表1所示.

表1 各模型預測精度對比

圖7 各模型預測結果對比

圖8 各模型預測結果對比

綜上可知，組合模型相較于單一時間序列模型在對河流水質指標中的化學需氧量和氨氮進行預測時的精度都有了明顯提高.其中ARIMA和LSTM組合模型比ARIMA模型的預測精度提高了約7%，SARIMA和LSTM組合模型比SARIMA模型的預測精度提高了約6%，SARIMA和LSTM組合模型的預測精度比ARIMA和LSTM組合模型的預測精度提高了約2%.所以，經過試驗分析，在本次試驗數據集的基礎上得到的河流水質預測最優模型為SARIMA和LSTM組合模型，該模型預測準確度較高，泛化能力強.

4 結 論

傳統的時間序列模型ARIMA和SARIMA能夠較好的體現時間序列數據中的線性特征，LSTM模型能夠很好的處理時間序列數據中的非線性特征，本文在使用ARIMA模型和SARIMA模型建模的基礎上提出了ARIMA和LSTM組合模型以及SARIMA和LSTM組合模型，并進行了實驗分析.經過實驗分析可知，組合模型對于河流水質指標中的化學需氧量和氨氮的預測精度優于單一時間序列模型的預測精度.SARIMA模型在ARIMA模型的基礎上增加了季節項，由于考慮了季節性因素對河流水質變化的影響，SARIMA模型的預測精度優于ARIMA模型.SARIMA與LSTM組合模型的預測精度比ARIMA模型的預測精度提高了10%左右，能夠較為準確的擬合以及預測河流水質參數指標，從而為保護河流水環境提供較為準確的參考依據.